地下结构地震反应分析中确定侧向边界的等效土柱模型

田树刚 陈清军,*

(1.同济大学土木工程防灾国家重点实验室,上海 200092; 2.同济大学结构工程与防灾研究所,上海 200092)

0 引 言

土-结构动力相互作用问题中土体边界条件的设置方式以及远场地基土体的简化模型有较大的研究价值和较强的研究意义。研究土-结构动力相互作用问题过程中的一个关键环节是对人工边界的处理,一般做法是从无限地基域割离出一定范围的近场地基,近似地认为这一部分地基土体对结构动力反应的影响代表了无限地基域对结构的影响。这样就引出了人工截断边界的问题。在截断边界上存在波的反射,反过来影响结构的反应,有阻尼时,这种反射波的能量逐渐被阻尼消散,无阻尼时,其将在土-结构系统内震荡。

如何降低土-结构动力相互作用问题中人工截断边界处波动反射的影响是一个热点研究课题。目前已有一些方法可以一定程度的解决这个问题,其中黏弹性人工边界方法是一种应用较多的边界处理方法,能达到有效的耗能目的,如文献[1-2]在高拱坝及地铁车站的地震响应的影响因素分析中应用了黏弹性人工边界条件来解决边界反射问题,文献[3-4]在土-桥梁结构及土-风电塔结构的动力相互作用分析中使用了黏弹性人工边界作为透射边界,文献[5-6]将黏弹性人工边界应用到悬臂挡土墙及高架罐体的土结构动力相互作用研究中。文献[7-8]研究了成层地基黏弹性人工边界的波动输入方法及多源输入条件下的黏弹性人工边界方法等。研究表明,动力无限元边界条件也能较好的实现从有限元到无限元的能量衰减效果,如文献[9]在高速铁路路堤震动问题的研究中应用了动力无限元边界,文献[10]将动力无限元边界条件应用于不同几何类型及底层条件的边坡的地震放大效应的研究中,文献[11]在研究地下工程数值计算中输入地震动的方法中应用了动力无限元单元作为人工截断边界条件,文献[12]研究了ABAQUS中的动力无限远人工边界的基本原理等。在地基土体的人工截断边界的处理中,远置侧向边界条件也被广泛使用,其中一个主要的研究点是侧向边界尺寸的确定,如文献[13]对土层随机地震反应分析中侧向人工边界的选取进行了研究,提出了确定土体侧向边界尺寸的方法,文献[14]研究了水平成层土层有限土层范围的选取对计算精度的影响,并应于与河谷上拱形结构的动力计算中。土-结构相互作用问题中,狭义的边界条件只是为了减弱边界波动反射对结构的影响而设置,如远置自由边界,耗能边界,透射边界等,广义的边界条件也可以包括两步法(子结构方法)的推广,等效处理远场地基土对近场地基-结构体系的作用。如文献[15-17]提出的土-结构动力相互作用的简化计算模型,保留近场地基,远场土用理想匹配土层PML (perfect matched layer)代替,并通过阻抗函数(impedance function)来近似确定远场土对近场土-结构的作用,并用与频率相关的刚度系数和阻尼系数来实现。耗能边界的设置可减小计算量,但其应用需要一些额外工作和一些特殊的输入方法。远置自由边界对于大型土-结构相互作用问题的计算成本较高,但对于小型或者一些简单的二维模型计算成本相对可以接受且操作简单,其物理模型更接近真实情况,能达到与设置了耗能边界模型相近的计算效果。

本文基于弹性波在水平成层土层中的传播理论,提出一种操作简单的确定土-结构动力相互作用问题中土体自由边界尺寸的等效土柱模型方法,以一个土-地下隧道结构为例,通过等效土柱模型方法确定了其合理的土体自由边界尺寸,并与粘弹性人工边界近似法及动力无限元边界方法的计算结果进行了对比印证,分析了不同边界条件的设置对隧道结构地震反应的影响,同时为解决土-结构动力相互作用问题中边界条件的设置提供了一定的参考。

1 基本理论与方法

1.1 问题描述

在土-结构动力相互作用问题中,往往人为切割出部分近场土域地基作为无限地基土体对结构作用的近似。图1为实际无限半空间模型及人工截断模型示意。

图1 土-结构相互作用体系土体人工边界处理Fig.1 Half space soil foundation and artificial soil boundary

需要寻求适当的方法来解决弹性波在人工截断边界上的传播问题,如不对截断边界做特殊处理,在其上会产生波的反射,反过来导致结构的附加反应,需把这种边界反射效应降低到可接受的范围。处理这个问题最简单的方法是设置远置自由人工边界,即土体横向范围取得足够远。远置自由边界尺寸的选取需满足两方面的要求:一是尺寸不能太大以至增加计算量,费时;二是尺寸不能太小,以至不能将边界反射对结构的影响降低到一定程度。

1.2 等效土柱模型确定水平成层土体自由边界尺寸

在土-地下结构动力相互作用问题中,地下结构的存在对土-结构体系在其人工截断边界部位的土体反应是有影响的,但这种影响随着人工截断边界尺寸的增加呈现逐渐减小的趋势,且逐渐趋近于水平成层的无限半空间土体受相同激励下的反应,而水平成层无限半空间土体可以用等效土柱代替。地震工程中常将覆盖土层及下卧基岩简化为物理力学指标竖向成层变化,横向均匀的半无限空间[18],据文献[19-20]对波在土柱中的传播理论的阐述,如果只考虑地震动的水平分量,则地震波在水平土层中的传播就可以简化为剪切运动,即与土柱轴向垂直的横向运动(u)在土柱中的传播。置于基岩上的水平土层如图2所示,假设基岩输入位移为ug(t),则距离土体顶部z深度处dz部分土柱隔离体上所受的力主要有惯性力、黏性力以及上下相邻土体作用其上的剪力的差值,其运动方程为[19]:

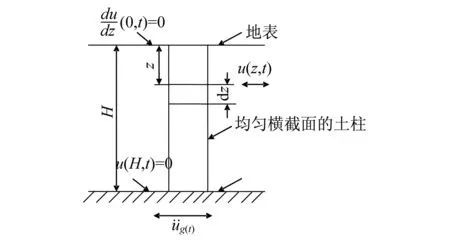
图2 基岩输入水平剪切地震作用时半无限土层截面及其边界条件Fig.2 Half space soil layer and its boundary conditions

(1)

其中,上下相邻土体对隔离体剪力的差值为

(2)

方程的解可以表达为

(3)

式(3)中Xn(t)满足如下条件:

(4)

式(4)可用逐步积分法求解,如Newmark 方法等。在水平单向输入地震动作用下,土柱运动方程的解也是与其对应的水平成层半无限空间土体运动方程的解。基于以上推理,提出一种简单的确定土体自由边界尺寸的方法。该方法的主要思路是建立土体侧向边界尺寸为大于10倍、20倍及30倍地下结构横向尺寸的整数的土-结构相互作用模型及同条件下可以代表水平成层的半无限空间的等效土柱模型,见图3,对二者输入相同的地震动,对比土柱与土-结构体系土域边界处顶部土体反应即图中的输出a和输出b,计算二者的相对误差,并建立相对误差随土-结构相互作用模型土体侧向边界尺寸的回归曲线,反过来可以通过该回归曲线标定相对误差为5%时的土-结构相互作用模型的土体侧向边界尺寸。所选取的比较参照点是基于认为在基岩输入地震动作用下,土-结构相互作用体系中的远场土体反应与代表无限半空间土柱的土体反应接近时,结构的存在对远场土体的反应影响甚微,反过来认为所取的土体尺寸已经足够大,波的边界反射效应对结构反应影响甚小这一逻辑。需指出这里暂未考虑半无限空间出平面SH波的影响。当有土层的剪切模量比及阻尼比与剪应变的关系曲线数据时,等效土柱模型可以用SHAKE或EERA等土层等效线性化动力分析程序代替,如上相同的操作同样可以确定土-结构动力相互作用模型的土体侧向边界的尺寸。

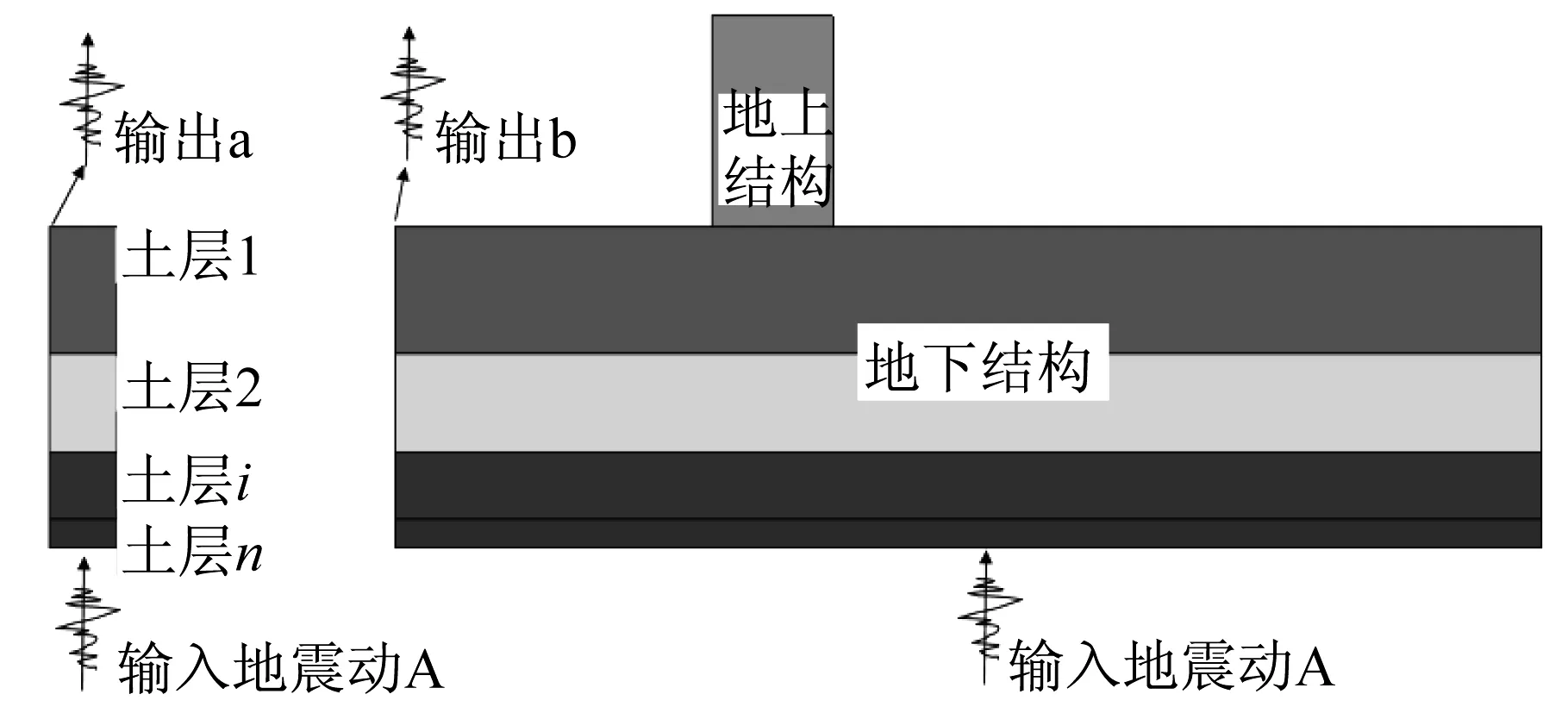
图3 水平成层无限半空间等效土柱校准土-结构相互作用体系土体边界示意Fig.3 Half space soil foundation and artificial soil boundary

1.3 黏弹性人工边界近似法及动力无限元边界方法

以下列出黏弹性人工边界近似法的边界元件刚度及阻尼系数的基本公式,罗列了动力无限元边界的基本方程及其在ABAQUS中的实现。

1.3.1黏弹性人工边界近似法

二维黏弹性人工边界在ABAQUS中的边界弹簧的切向的弹簧的刚度系数KT和阻尼系数CT及法向弹簧的刚度KN和阻尼系数CN见公式(5)[8]。

(5)

地震波在土层中的纵波及横波波速见式(6)

(6)

式中:ρi为第i层土的密度;r为人工边界点到波源的距离,近似可以取近场结构几何中心到要施加人工边界的边界线或者边界面的距离;λ和G为拉梅常数;E和μ分别为弹性模量和泊松比,以上均满足i=1～n,分别代表自上而下的各大类地基土层;αT和αN为相关的系数。

黏弹性人工边界的输入需要做一些特殊处理,需以等效荷载的形式施加在底部边界和侧向边界上,等效荷载计算公式及输入方法可参考文献[20]等。

1.3.2动力无限元边界

ABAQUS软件自带一种吸能边界单元-无限元单元,是由无限元静力人工边界和黏性动力吸收边界组合而成,该单元能够较好地模拟无限地基的辐射阻尼且能模拟无限远处位移为零的边界条件[21]。ABAQUS动力分析中的无限元是基于Lysmer和Kuhlemeyer的研究成果。动力分析中无限元的材料是线弹性的,其平衡方程为

(7)

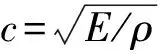
(8)

界面上的阻尼力为

(9)

式中:d是阻尼系数。

(10)

三维情形只需更改一下波速的公式,即

(11)

按式(11)计算阻尼系数即可实现边界上无反射波的条件。ABAQUS中无限元的设置需要结合CAE和修改Input文件同时操作来实现。在CAE中,有限元和无限元可只建一个Part,后用Partition工具将有限元与无限元分离。无限元的材料特性与其对应的有限元部分的线弹性部分一致,定义属于无限元的Section上选择与其相应的线弹性材料,后将其赋予对应的无限元区域。无限元的Mesh Control选Sweep技术,Sweep的方向指向无限地基域的方向,且沿其长度方向只划分一个单元。为做区分,无限元单元类型可以选择与有限元部分不一致的单元类型,例如,有限元单元类型为CPE4R,无限元的单元类型可以设置为CPE4RH,或者选Acoustic单元AC2D4(三维情形选AC3D8R)。写Input文件,将Input文件中的无限元单元类型改成CINPE4 (三维为CIN3D8),将更改后的Input文件提交求解器计算。假设从有限元-无限元交界处输入的地震动即为实际传播到模型基岩处的地震动,由于无限元单元只是对从有限元区域向外传播的波有效,如此能满足内源入射的假定,其输入方式以等效力的形式输入。需明确的是,为模型施加了无限元单元相当于已经为模型施加了边界条件,故除了在模型土体底部有限元与无限元交界处输入地震动之外,无须再施加其他边界约束条件,这里暂未考虑外域地震波动对无限地基域辐射阻尼的影响。

2 算例

2.1 工程背景及数值模型

以某沉管隧道工程为背景,应用等效土柱方法确定其侧向自由边界尺寸,并与黏弹性人工边界近似法及动力无限元边界的计算结果进行了对比。该工程隧道典型横截面设计见图4。

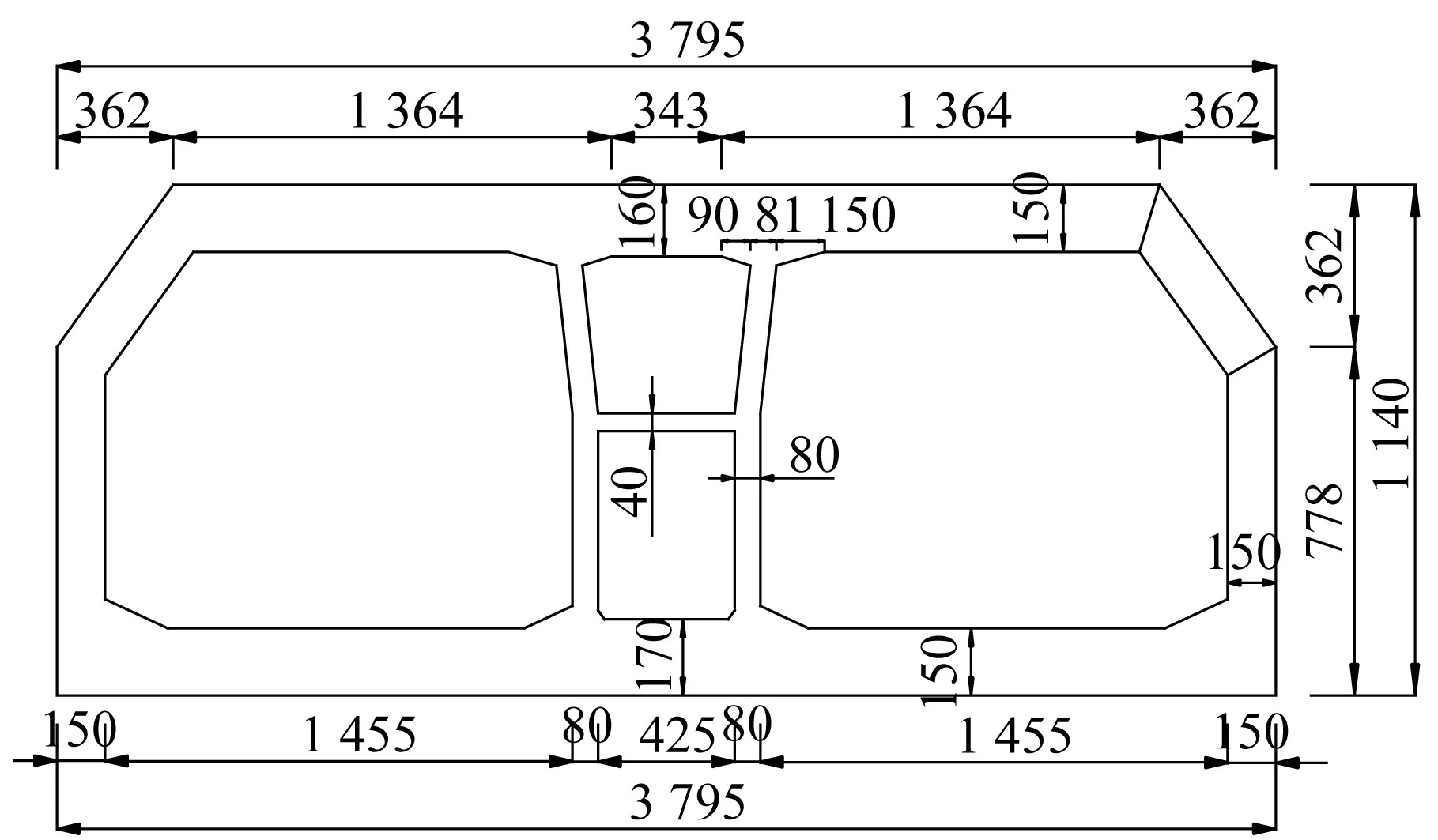
图4 隧道典型横断面设计图(单位:cm)Fig.4 Representative cross section of immersed tube tunnel (Unit:cm)

据地勘提供的土层资料,将隧道场区土层归为四大土类,自上而下分别是淤泥、粉质黏土、粉细砂及粗砂、风化岩。土层材料物理力学指标列于表1。

表1土层材料参数表

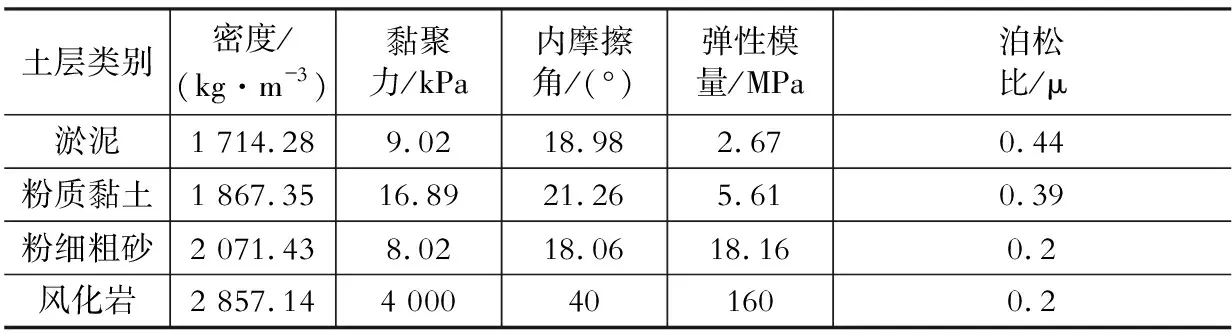
Table 1 Parameter table of soil

土体采用基于摩尔库伦准则的理想弹塑性本构模型,并选用四节点四边形双线性平面应变单元(CPE4R)。工程桩采用线弹性本构模型,隧道周围一般回填固定碎石、隧道底部的碎石垫层以及两侧的锁定回填碎石均选用线弹性本构模型,隧道混凝土采用塑性损伤本构模型,该模型材料参数见表2。

表2混凝土塑性损伤本构模型参数

Table 2 Concrete Damaged Plasticity model parameters

考虑到剪切波从基岩垂直入射,沿土层深度方向土层网格尺寸需满足一定条件。这里,土层竖向网格尺寸需满足

(12)

式中:Lmesh为沿土层深度方向的最大网格尺寸;Lwave为地震波的波长;Vs为土层的剪切波速,理论上应以所有土层最小剪切波速来控制最大网格尺寸,依据勘察单位提供的剪切波速测试报告,取Vs=104.6 m/s;fcontrol为输入地震动的控制频率,这里fcontrol取15 Hz。

最终沿土体深度方向网格尺寸定为0.8 m,模型横向网格尺寸可以设定为沿深度方向网格尺寸的3～5倍,这里设定为4 m。

地基土体深度依勘察结果取102.3 m,据文献[14]的建议,地基土体的长深比应大于7,即最小横向尺寸应大于716.1 m。为实现本文提出的确定地基横向尺寸的方法,依照地基横向尺寸不同分别建立10倍、20倍及30倍隧道横向尺寸的模型,即分别为379.5 m,759 m,1 138.5 m,为方便可取整数即400 m、800 m (大于716.1 m)及1 200 m三种尺寸的远置边界模型。400 m地基土体-地下结构相互作用模型如图5上右图所示,1 200 m地基土体-地下结构相互作用模型见图5下,同时建立一个代表水平成层的半无限空间地基的等效土柱模型,土柱模型如图5上左图所示,其土层划分以及输入地震动情况均与设置侧向边界的土-地下结构模型相同。

据工程场地设计地震动参数研究报告[22],选取多遇地震情形(ODE),即120年超越概率63%的地震动进行计算,调整输入地震动的幅值为0.53 m/s2。选取El Centro和Kobe 及该工程设计地震动参数研究报中的一条人工波GZA作为输入地震动,输入地震动加速度时程见图6。

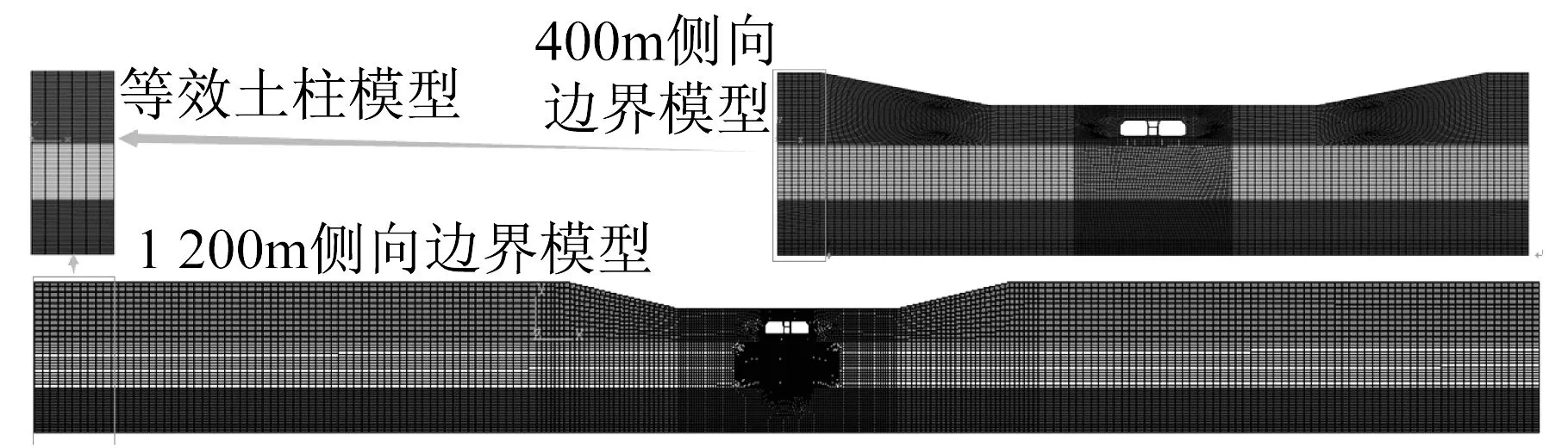
图5 等效无限半空间地基土柱模型及地基-地下隧道结构远置旁轴边界模型Fig.5 FE Model of horizontal layered half space soil column and foundation-tunnel far boundary interaction system

图6 输入地震动加速度时程Fig.6 Input ground motion and its Fourier spectrum

2.2 等效土柱模型确定土-隧道体系侧向边界

经计算,土柱的土层顶部加速度反应时程与设置了不同侧向边界尺寸的土-结构体系土体左侧边界顶部的加速度反应时程对比如图7所示,土柱模型的顶部反应与400 m侧向边界模型的土体顶部反应差值相对是最大的,随着土-结构体系侧向边界尺寸的增大,这种差异逐渐减小,当增至1 200 m时,二者加速度反应基本一致,说明当不做其他吸能或透射边界处理时,此隧道工程的土体侧向边界尺寸取1 200 m即可基本忽略边界反射的影响。

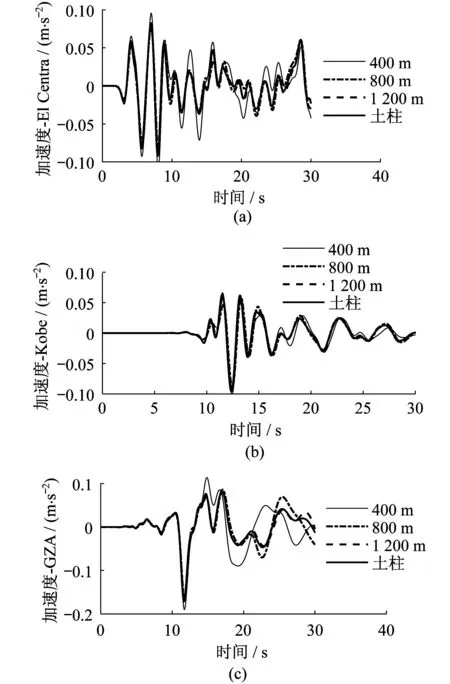
图7 不同远置边界尺寸模型与半无限空间土柱模型加速度反应对比Fig.7 Comparison of response acceleration at soil corner between soil column and tunnel-soil systems

由图8可知,土柱模型的顶部位移反应与400 m侧向边界模型的土体顶部位移反应相对是最大的,且比二者加速度反应的差异更明显。随着侧向边界尺寸的增大,这种差异逐渐减小,直至土体侧向边界尺寸增至1 200 m时,二者位移反应基本一致,图9更清楚地表达了三种尺寸的侧向边界模型加速度反应及位移反应与土柱的同项目反应绝对误差的递增序列,得到的加速度及位移的误差符合预期规律,即随土-结构相互作用模型侧向边界尺寸的增加,土-结构相互作用体系人工截断边界处土层顶部的位移和加速度反应与能代表办无限空间的土柱顶部的土体反应的相对误差是减小的规律。当侧向边界为1 200 m时,三条波输入下的加速度及位移的相对误差均相对较小。

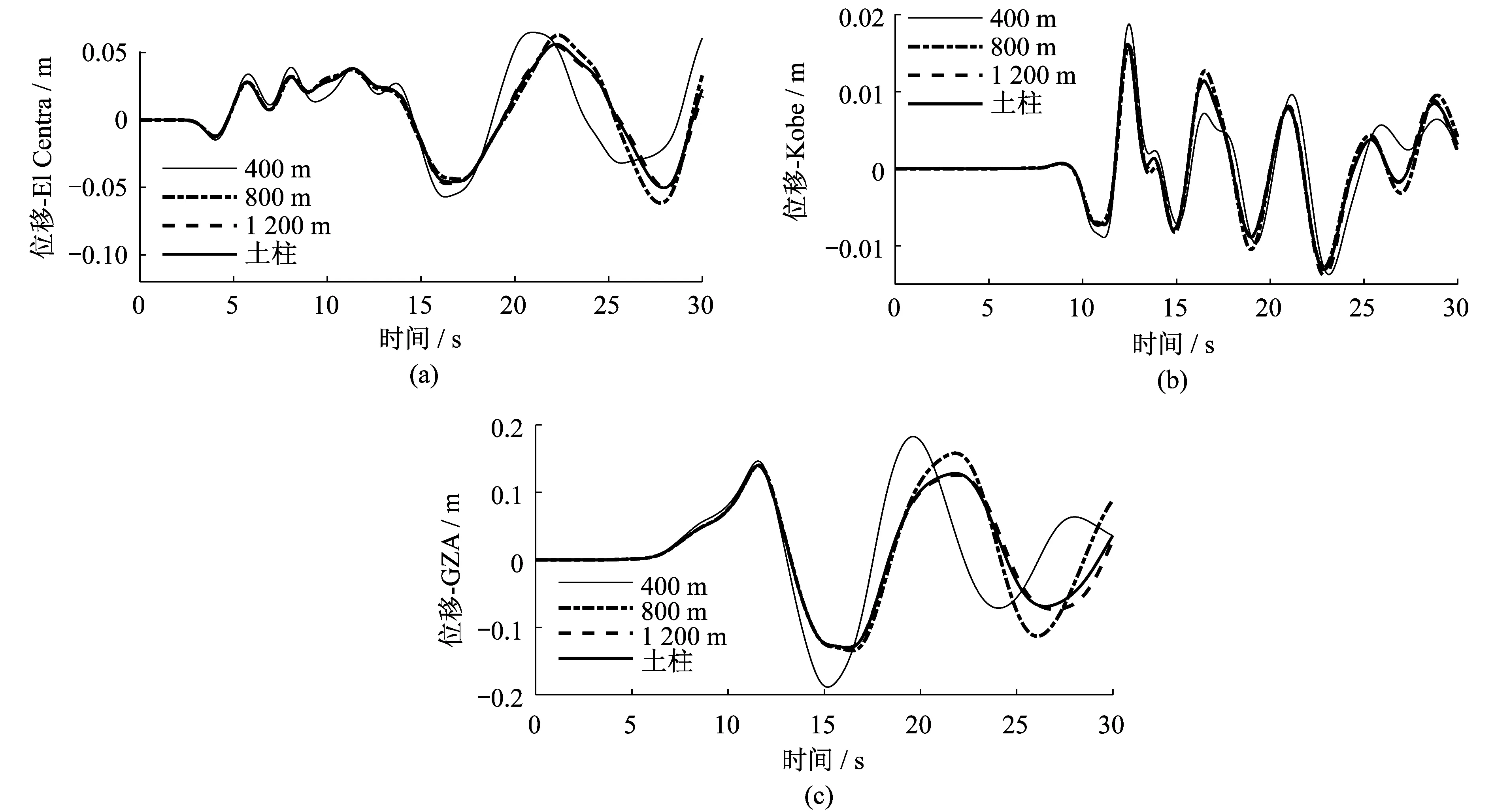
图8 不同远置边界尺寸模型与半无限空间土柱模型位移反应时程对比/mFig.8 Comparison of response displacement at soil corner between soil column and tunnel-soil system/m

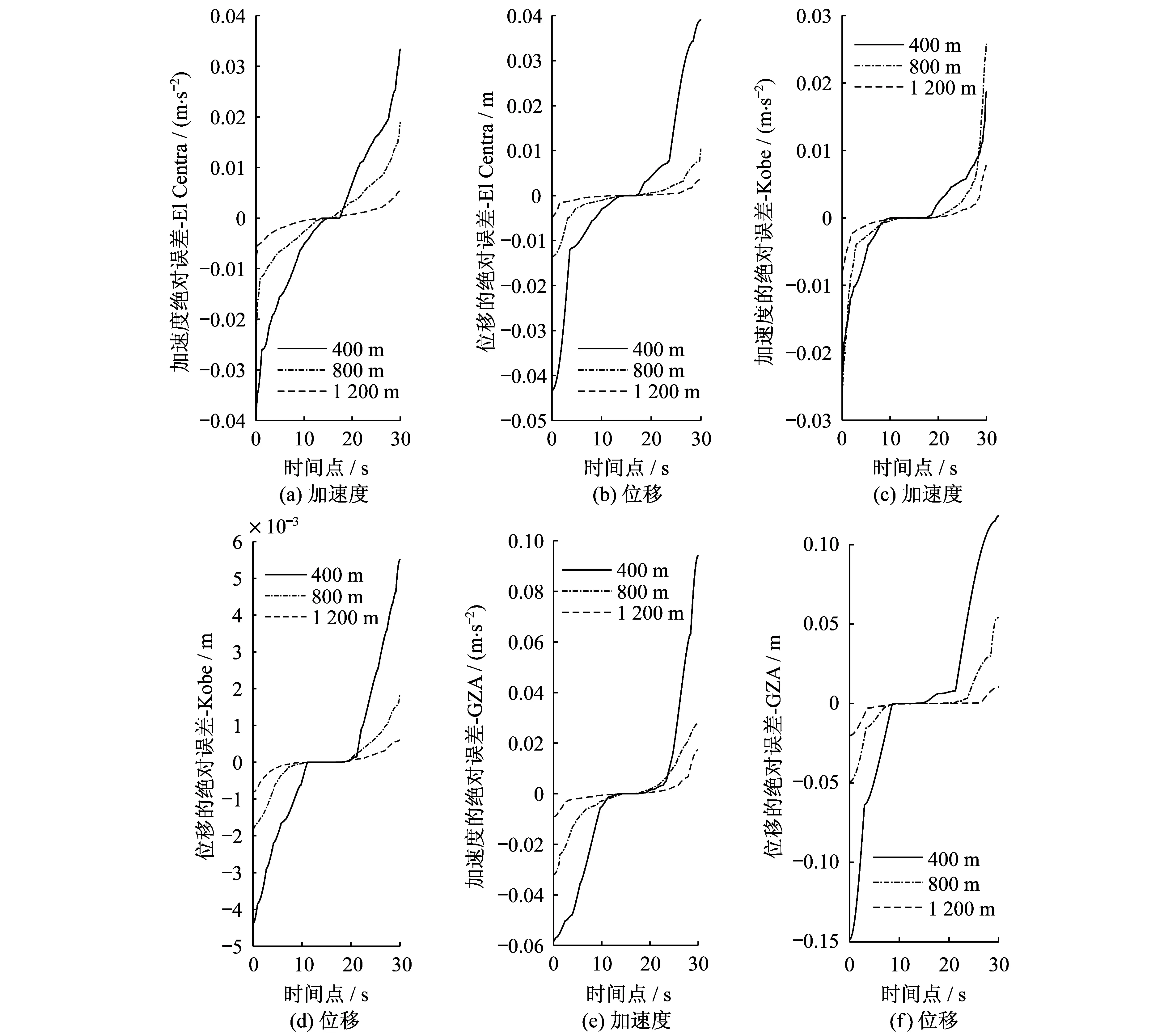
图9 绝对误差的递增序列Fig.9 Difference between far boundary model and soil column

土-结构相互作用体系与等效土柱的相对误差对比见图10,从图10(a)及图10(b)的相对误差直方图可见,随着土-结构相互作用体系土体侧向边界尺寸的增加,加速度和位移的相对误差是减小的规律。以三条波的均值相对误差为基础进行线性回归的结果见图10(c),得到回归方程后,可以得到满足相对误差为5%时所需的结构侧向边界尺寸。当相对误差等于工程误差5%时,本例模型基于位移的相对误差回归曲线得到的土体边界尺寸为1 012.53 m (约27倍隧道横截面横向尺寸),基于加速度的相对误差回归曲线得到的土体边界尺寸为945.91 m (约25倍隧道横截面横向尺寸)。如果想控制相对误差为2%以内,基于加速度校准的边界尺寸至少应为1 173.48 m (约30倍隧道横截面横向尺寸),基于位移校准的边界尺寸至少应为1 125.74 m (约31倍隧道横截面横向尺寸)。如果想消除这种相对误差,土体侧向边界尺寸至少应为1 325 m (32倍隧道横截面横向尺寸)。 最终采用等效土柱模型方法近似确定的地基-隧道相互作用体系的土体侧向自由边界尺寸选择为1 200 m时,可以控制相对误差在2%以内。

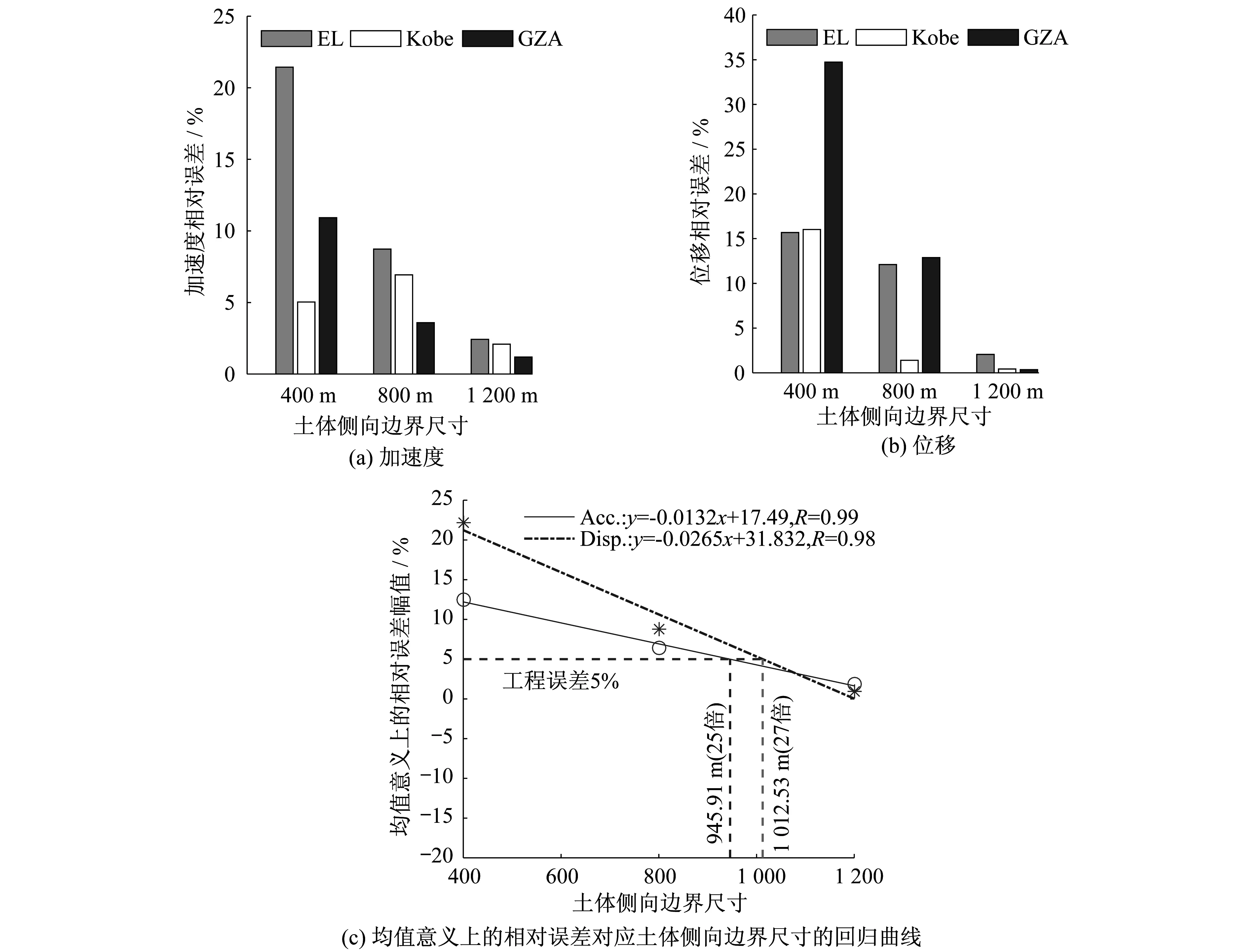
图10 相对误差对比/%Fig.10 Relative Error between far boundary model and soil column/%

表3相对误差对比表

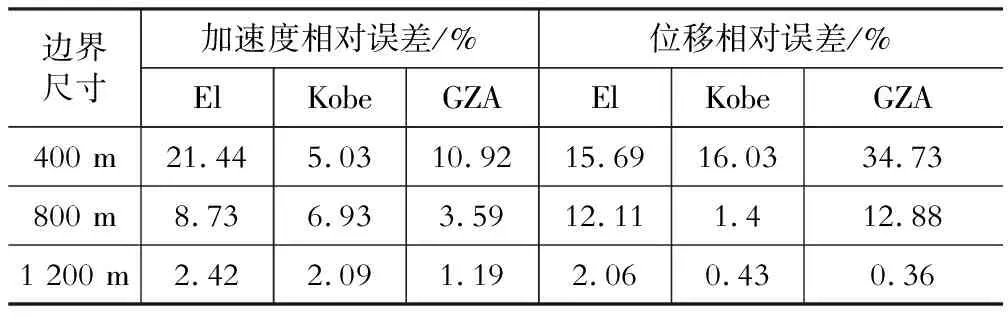
Table 3 Relative error

3 等效土柱模型确定的侧向自由边界与耗能边界的对比

这里选用黏弹性人工边界近似法及动力无限元边界进行对比印证由等效土柱模型确定的侧向自由边界模型。据文献[13]的研究成果,在土-结构相互作用问题中,对于黏弹性边界模型,当土体长深比L/H>5时,相对误差可以控制在5%以内,本文所依托之隧道工程实际勘测土体最深处达102.3 m,故土体长度方向尺寸应大于511.5 m,这里取520 m。以520 m侧向自由边界模型为基础分别建立黏弹性人工边界模型及有限元-无限元边界模型,与前述确定的1 200 m (相对误差小于2%)侧向自由边界模型的结构地震反应进行了对比。

3.1 侧向自由边界与黏弹性人工边界近似法对比

据式(5)、式(6)可以确定二维黏弹性人工边界的输入参数即边界上弹簧单元的刚度系数和阻尼元件的阻尼系数,具体数值列于表4中。这里取i=1～4,分别代表自上而下的淤泥、粉质黏土、粉细砂及粗砂和风化岩四大类地基土层。式中αT的取值范围为[0.35～1.00],αN取值范围[0.8～2.0],这里参考文献[20,23],取αT=0.67,αN=1.33。

表4地基黏弹性人工边界参数

Table 4 Parameter table of viscoelastic boundary

对比采用等效土柱方法确定的1 200 m侧向自由边界模型与设置了粘弹性人工边界的模型的计算结果,以验证其合理性。选取隧道结构外侧顶部角点作为参考点进行结构反应的对比。有效应力反应时程对比如图11(a)所示,经计算知二者最大差异在0.06 MPa以内。

位移反应时程对比见图11(b),可知在20 s之前符合较好,22～28 s二者差异相对前部分稍大一些,最大差值为0.01 m。加速度反应时程对比见图11(c),总体来说,二者在整个过程中符合均较好,最大差值为0.006 m/s2。说明1 200 m侧向自由边界模型与设置了黏弹性人工边界模型的计算结果较为接近,侧向边界尺寸的选取是合理的。

3.2 侧向自由边界与动力无限元边界对比

基于520 m侧向自由边界尺寸的模型建立有限元-无限元模型,在有限元模型的底边和两个侧边施加一层无限元单元,如图12(a)所示,图12(b)为隧道周围网格划分局部放大图,隧道周边一般回填碎石范围内的局部土体网格做了细化。

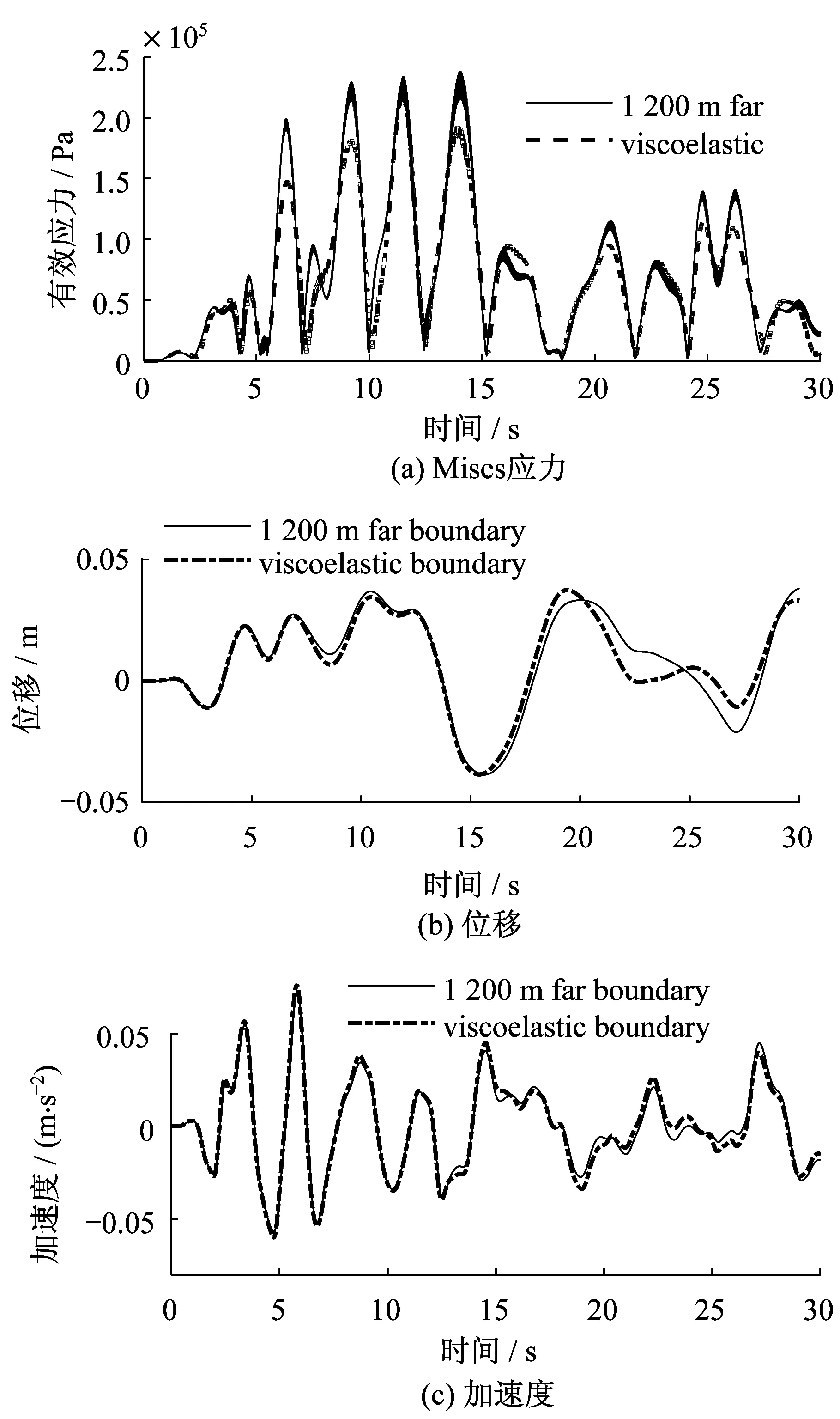
图11 侧向边界与黏弹性人工边界方法结构时程对比Fig.11 Compare of structural response between viscoelastic method and far boundary

施加了动力无限元边界单元之后,在某一典型时刻体系位移反应分布如图13所示,可见无限元部分有效地实现了对外行波的衰减,直至最外围几乎达到零值。

1 200 m侧向自由边界与无限元边界模型的Mises应力时程对比如图14(a)所示,二者符合较好。无限元模型与黏弹性边界模型在所选取的特征点的加速度及位移反应较为接近,基本一致,故1 200 m侧向边界模型与无限元模型的差异同前述其与黏弹性边界模型反应的差异。

侧向边界与耗能边界结构反应的绝对误差见图15,从图中可知各个分量的绝对误差均在合理范围内。

图12 隧道-地基有限元-无限元模型Fig.12 Finite-infinite element model of tunnel-foundation system

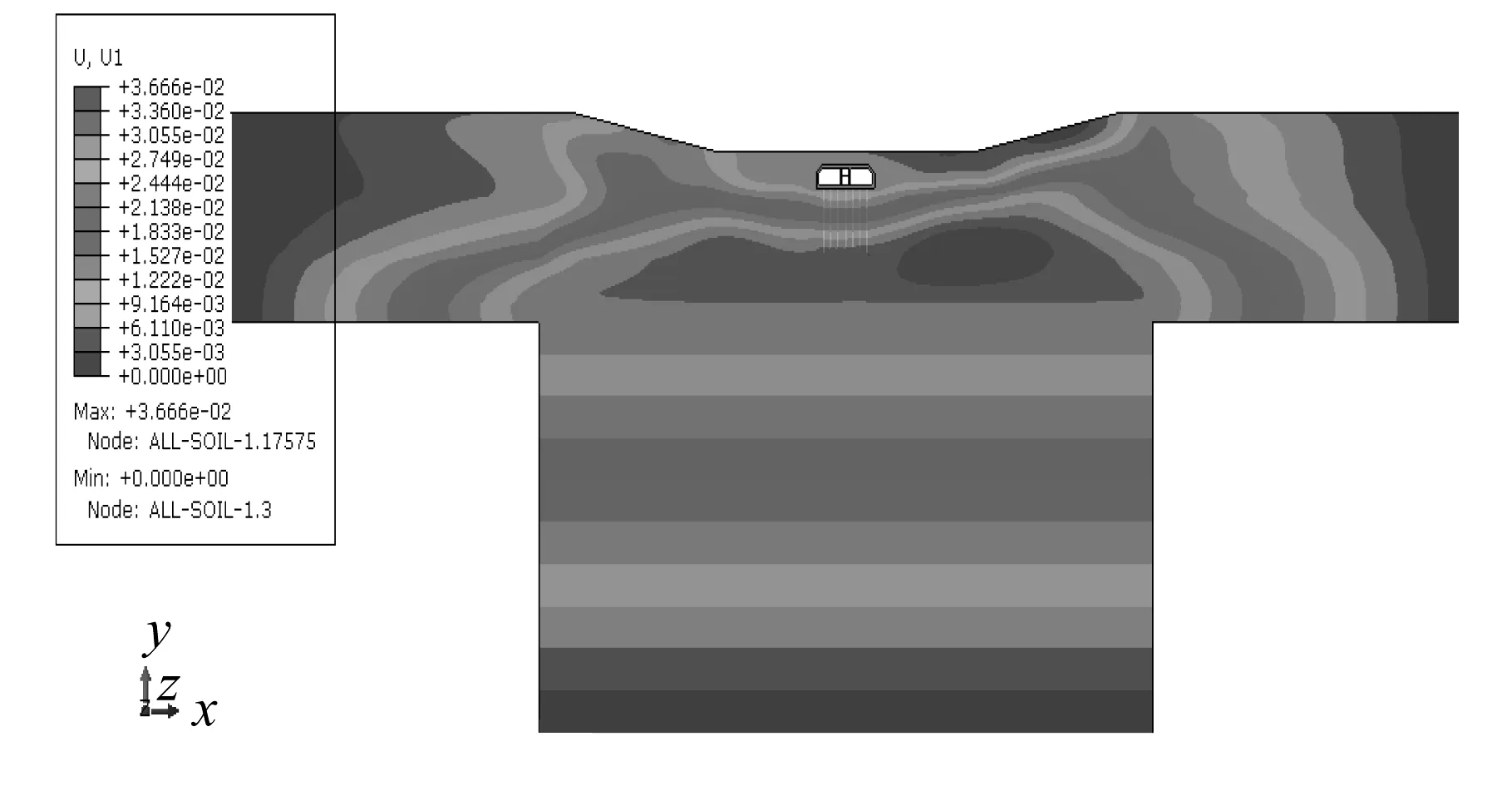
图13 有限元-无限元地基-隧道模型位移反应分布图/mFig.13 Response displacement distribution of finite-infinite foundation-tunnel model/m

结果表明三种边界处理方式的结构反应均较为接近,说明等效土柱方法确定的侧向自由边界模型基本能满足将边界反射波的影响降低到一定程度的要求,同时说明在土-结构动力相互作用问题中,无论是大尺寸侧向自由边界模型还是小尺寸加耗能边界的模型均能达到预期的对边界反射影响抑制的目的,但小尺寸侧向自由边界模型存在明显的边界反射的影响。需指出,以上均未考虑基础结构产生的散射波的影响。

4 结 论

图14 侧向边界与无限元边界方法结构时程对比Fig.14 Compare of structure response between infinite boundary and far boundary

基于弹性波在水平成层土层中传播的基本原理,提出了采用等效土柱模型校准确定土-结构相互作用问题中土体侧向自由边界尺寸的方法。以一个地下隧道工程为例,采用等效土柱模型确定了其侧向自由边界尺寸。后与黏弹性人工边界近似法及动力无限元边界方法进行了对比印证,同时考察了边界条件的设置对地下结构地震反应的影响。结果表明:

(1) 采用本文提出的方法,侧向边界改变三次就基本能确定合理的土体侧向边界的尺寸,且可得到相对误差与土体侧向边界尺寸的回归曲线。并基于该曲线计算出能满足工程误差5%的要求的土-结构相互作用体系的最小侧向边界尺寸,据相对误差曲线得到的土-结构相互作用体系的最小侧向边界尺寸为1 012.53 m,约等于27倍隧道横截面的横向尺寸。

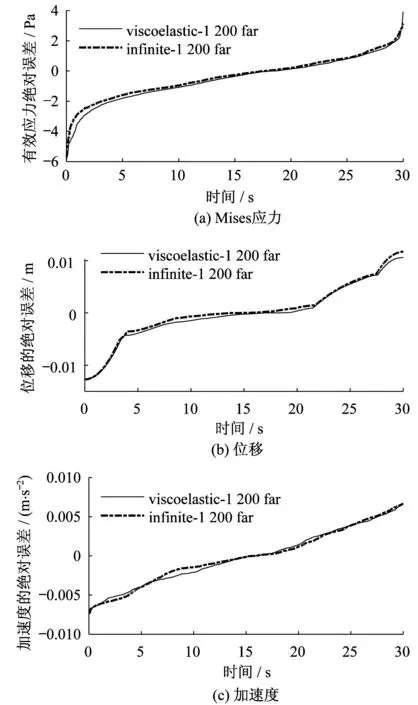
图15 侧向边界与耗能边界结构反应绝对误差的递增序列Fig.15 Error comparation of structure response between infinite boundary and far boundary

(2) 采用相对误差小于2%的1 200 m远置自由边界模型与黏弹性边界近似法及动力无限元边界模型的结构反应符合较好。

(3) 黏弹性边界近似法及动力无限元边界模型可以相对小的侧向自由边界尺寸达到与大尺寸侧向自由边界模型相近的计算精度的效果。

通过等效土柱模型确定土体侧向自由边界的方法为土-结构动力相互作用问题中土体侧向自由边界尺寸的确定提供了一种有效思路,同时文中所用其他边界处理方法也为土-地下结构相互作用问题中土体边界条件的设置提供了参考。对于复杂三维土-结构模型可采用黏弹性人工边界及动力无限元边界等耗能边界,以减小计算量,对简单二维平面问题可以选取以上三种任一种方法处理土体边界。