缩短飞行汽车起飞距离的一种滑跑新策略
2018-11-22林海英吴帅李泽宇
林海英 吴帅 李泽宇
(北京航空航天大学,北京 100191)
主题词:飞行汽车 车辆分析 起飞滑跑 动力学分析
1 前言
飞行汽车作为一种新概念交通工具已被提出多年,其特点为既可在地面上行驶又可在空中飞行。现有多数固定翼飞行汽车的起飞滑跑均需依靠螺旋桨提供动力:地面滑行时,发动机将动力输出至螺旋桨推动飞行汽车加速;车轮为随动部件提供地面支撑。
然而,低空速情况下螺旋桨存在推进效率低的特点。在相同发动机状态下,低空速时使用车轮提供驱动力往往比螺旋桨推动获得更大的加速度,提高发动机有效功率,提升燃油经济性。此外,与以气动力作为推力的飞行器相比,飞行汽车优势在于本身具有地面行驶的整套系统,可在不增加额外装置的情况下实现地面车轮加速滑跑。因此,研究飞行汽车车轮驱动的起飞滑跑方式具有一定的意义。
近年来,国外对于飞行汽车的研究多集中于概念设计[1-6];在飞行器滑跑距离优化方面,Kobayashi等[7]介绍了一种电动助力的飞机起飞滑跑方式,它采用螺旋桨和电动车轮联合驱动;美国国家航空航天局兰利研究中心(NASA Langley Research Center)对波音公司某型飞机进行相关研究试验,论证了助力滑跑的可行性。在国内,吴大卫等[8]通过改变升降舵等的控制操纵策略优化了某种小型飞机的起飞距离;王健等[9]进行了某型短距起飞垂直着陆飞机的滑跑建模与仿真计算,并与试验数据进行了分析对比;宋花玉等[10]提出了飞机起飞滑跑距离数值积分改进算法,算法精度更高;石坚等[11]进行了汽车加速工况的仿真试验;聂宏[12]进行了舰载飞机弹射起飞的动力学研究进展研究。然而针对具有车轮驱动能力的飞行汽车,起飞滑跑距离优化方面的研究仍然较少。
本文介绍了一种使用车轮加速的飞行汽车起飞滑跑方案,运用MATLAB建立动力学模型对起飞过程进行仿真研究,得到车轮-螺旋桨混合驱动、只使用螺旋桨驱动两种不同驱动策略下的起飞滑跑距离并进行对比。结果表明,混合驱动策略有效降低了起飞滑跑距离。
2 车轮-螺旋桨混合驱动滑跑状态分析
2.1 整车状态构型
飞行汽车在起飞滑跑时的整车状态如图1所示,机翼、尾翼、螺旋桨已处在完全展开位置。机翼为全动机翼,能够以翼展方向为轴进行旋转改变机翼迎角。

图1 整车状态
2.2 车轮-螺旋桨混合驱动的滑跑过程
该起飞滑跑过程包括5个阶段:
a.起步阶段。飞行汽车从静止加速至最低挡稳定车速,其间动力系统依靠离合器摩擦输出动力。此阶段及后续车轮驱动滑跑阶段机翼攻角为负,提供负升力。
b.车轮驱动滑跑阶段。此阶段为飞行汽车的主要加速阶段。加速时使用较低挡位以获取较大驱动力,车速达到所在挡位能够提供的最高车速时即升入更高挡。
c.动力切换阶段。在滑跑过程后段,发动机输出的动力由车轮转换至螺旋桨,该过程为动态过程。通过传动系统调节,车轮驱动力逐渐减小,螺旋桨驱动力逐渐增大,直至螺旋桨达到最大转速,此时飞行汽车驱动力全部来自螺旋桨。该阶段中全动机翼的攻角也由负调节为正,机翼从为整车提供下压力变为提供升力。
d.螺旋桨驱动滑跑阶段。该阶段中螺旋桨驱动飞行汽车达到起飞离地临界速度。
e.抬前轮的两轮滑跑阶段。其与常规飞机抬前轮滑跑过程相似,根据工程经验,其持续时间常以3 s估算。
表1列出了起飞滑跑过程中各阶段的特点。
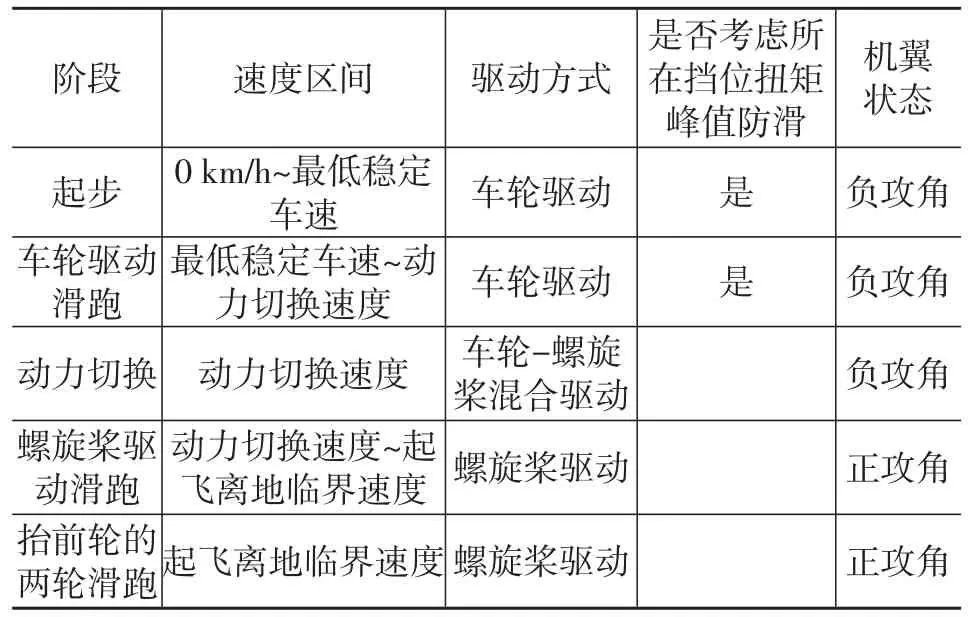
表1 起飞滑跑各阶段特点
2.3 驱动轮防滑策略
导致驱动轮打滑的因素主要分为3个方面:首先,为获得较大航程,飞行汽车的整备质量普遍较轻,易出现高速条件下驱动轮附着力不足的情况;其次,为保证飞行汽车良好的飞行性能并随时应对突发情况,其航空发动机后备功率往往较大,过高的发动机功率输出容易以大扭矩形式作用于驱动轮,导致各挡位扭矩峰值附近驱动轮打滑;最后,随滑跑速度上升,机翼升力提高,整车下压力降低,尤其在车速逼近起飞离地临界速度时,整车下压力几乎为零,驱动轮完全打滑无法输出动力。
为避免打滑,降低发动机节气门开度是最有效的方法,但发动机输出功率的降低会增加飞行汽车的起飞滑跑距离。因此,在低车速和高车速时采用不同的防滑策略:在低车速阶段,负攻角的全动机翼能够提供的下压力较小,因此需通过降低发动机节气门开度来削减驱动力以避免打滑;在车速较高的阶段,可绕机翼翼展方向旋转的全动机翼能够减小机翼攻角至负值以提供足够的负升力,避免了降低发动机节气门开度造成的发动机功率下降。
3 动力学特性分析
3.1 动力学模型假设
为简化计算模型,进行如下假设:因机场跑道路况普遍良好,假设飞行汽车起飞滑跑过程中道路水平无坡度,忽略坡度阻力;考虑到换挡时间较短,假设变速器换挡瞬时完成,忽略因离合器接合引起的驱动力波动。
3.2 动力学模型建立
3.2.1 滑跑中各力计算
参考汽车理论[13]及飞机设计手册[14]建立飞行汽车起飞滑跑数学模型。发动机转矩和车轮驱动力分别为:
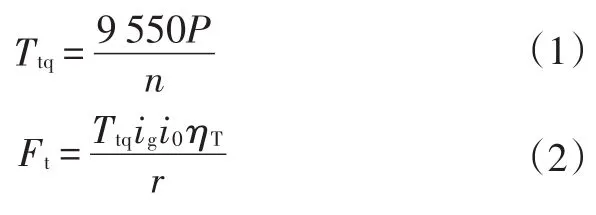
式中,P为发动机功率;n为转速;ig、i0分别为变速器和主减速器传动比;r为轮胎半径,ηT为传动系机械效率。
根据流体动压方程,升力为:

式中,S为机翼面积;v为车速;ρ为空气密度;C为升力系数。
升力系数C与机翼攻角α的关系为:
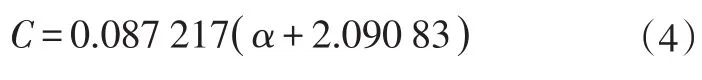
剩余重力Gm和滚动阻力Ff分别为:


式中,G为整车重力;f为滚动摩擦因数。
整车风阻Fw主要包括车身空气阻力Fw1、机翼空气阻力Fw2以及螺旋桨空气阻力Fw3:
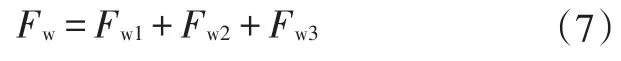
前后轮静态轴荷的法向反作用力分别为:
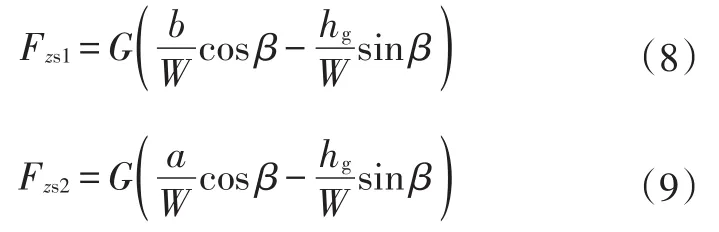
式中,hg为重心高度;W为轴距;β为爬坡角度;a、b分别为重心距前后轴距离。
前、后轴法向作用力分别为:

式中,Fzw1、Fzw2分别为车身引起的前、后轴的气动升力;m为整车整备质量;u为车速。
车轮能够提供的附着力为:

式中,Fz为法向反作用力;φ为地面附着系数。
3.2.2 起飞离地临界速度计算
受擦地角、飞行员视野限制,飞行汽车离地速度为:
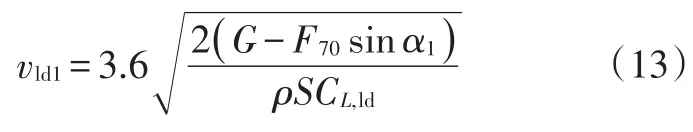
式中,α1为起飞迎角;CL,ld为飞行汽车在起飞离地速度时的升力系数;F70为70%离地速度时动力装置推力。
受失速速度限制的离地速度为:
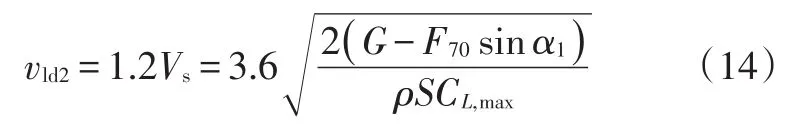
式中,CL,max为最大升力系数;Vs为最小失速速度。
起飞离地临界速度Vld取Vld1与Vld2中的较大值。
3.2.3 车轮驱动下的滑跑距离
起步阶段与动力切换阶段时间较短,滑跑距离可根据现有乘用车的数据及工程经验进行估算。
车轮驱动的加速度为:
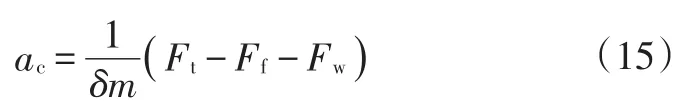
式中,δ为质量换算系数。
车轮驱动下的滑跑距离l1计算为:


在螺旋桨驱动阶段,滑跑距离的计算同样采用上述积分的方式进行,只需将车轮驱动力Ft修改为螺旋桨动力Fp,将各阻力值作相应变化。
抬前轮滑跑阶段加速距离l2由经验公式得到:
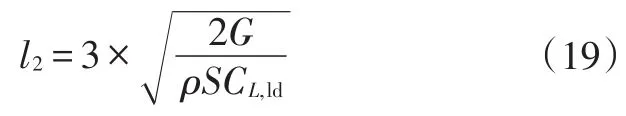
使用车轮驱动加速的总滑跑距离l为:
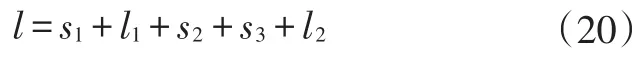
式中,s1、s2、s3分别为起步阶段、动力切换阶段、螺旋桨驱动阶段滑跑距离。
3.2.4 螺旋桨驱动的滑跑距离
螺旋桨驱动的飞行汽车在起飞滑跑时包括四轮滑跑阶段和抬前轮的两轮滑跑阶段。后一阶段滑跑距离的计算与车轮驱动下的l2相同。前一阶段的滑跑距离计算:
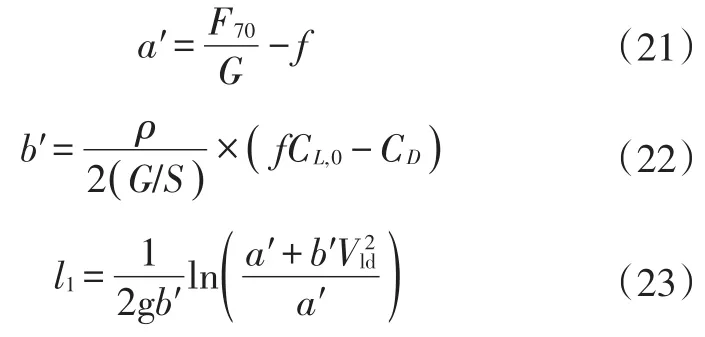
式中,CL,0为四轮滑跑升力系数。
4 起飞滑跑实例计算
4.1 计算针对的速度区间
在抬前轮的两轮滑跑阶段,两种驱动方式均采用螺旋桨驱动,驱动距离没有差异,因此只需在起步加速至起飞离地临界速度的速度区间计算滑跑距离便可进行两种不同滑跑形式的对比分析。
4.2 整车参数
飞行汽车发动机采用Rotax914航空活塞发动机,整车驱动方式为前轮驱动,具体参数如表2所示。
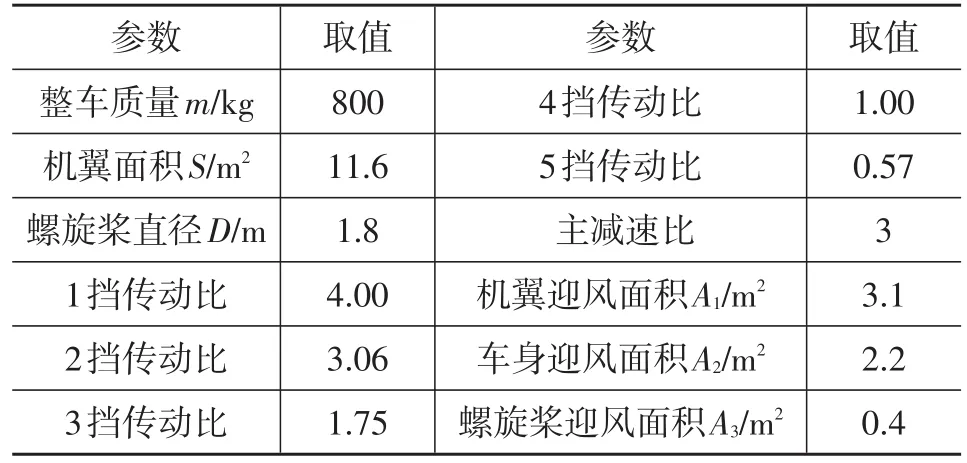
表2 飞行汽车参数
4.3 发动机转矩特性
图2所示为Rotax914发动机的60%、80%、100%及115%节气门开度下转矩外特性曲线。数据采集自发动机台架试验并通过最小二乘法进行多项式四阶曲线拟合,拟合精度平均值98.4%。

图2 Rotax914发动机扭矩特性曲线
4.4 计算简化
a. 根据毛务本的研究[15],一般车辆起步阶段从静止加速到最低稳定车速可按1~3 s估算。航空发动机功率大,在此估算其起步阶段历时2 s,且加速度恒定。
b.螺旋桨在起步及四轮滑跑两个阶段中无动力输出,其空气阻力Fw3的计算需考虑是否出现风车转动。马菲团队[16]对塞斯纳172型飞机进行试验后指出:空速93 km/h以下时,该型飞机采用的1.9 m螺旋桨无风车转动。飞行汽车采用更小桨径的1.8 m螺旋桨,在相同空速下按无风车转动简化螺旋桨空气阻力的计算。
c. 假设将动力从车轮切换至螺旋桨用时1 s,此过程飞行汽车保持匀速。
4.5 计算结果及分析
代入飞行汽车数据,应用MATLAB进行编程仿真。
4.5.1 最低稳定车速
本文飞行汽车使用的发动机慢车时最低稳定转速约为2 000 r/min,计算得到最低稳定车速为16.3 km/h。
4.5.2 起飞离地临界速度
经计算得出飞行汽车的起飞离地临界速度为102.4 km/h,将切换速度定义为102.4 km/h。
4.5.3 车轮驱动模式下的附着力与驱动力
车轮驱动滑跑阶段(16.3~70 km/h)的驱动力-最大附着力曲线如图3所示。驱动轮最大附着力曲线采用最高的115%节气门发动机转矩计算得出,以此节气门开度计算得出的最大附着力为最易发生打滑工况。令驱动力数值低于该工况下的最大附着力能够最大限度地防止打滑发生。该阶段全动机翼处于负迎角状态,因此,随着车速的增加最大附着力曲线成上升趋势。飞行汽车使用前3个挡位便可加速到起飞离地临界速度102.4 km/h。由于计算中忽略了离合器接合时间,驱动力在换挡时为瞬时突变。发动机在低转速高节气门开度的工况下工作不稳定,因此在最低稳定车速16.3 km/h至26.3 km/h的速度区间内采用60%的节气门保证发动机稳定工作。在26.3~49.3 km/h的车速阶段,115%节气门下的驱动力大于最大附着力,表明在115%节气门下该阶段会出现打滑现象,该速度阶段应使用100%节气门。以此类推,各速度区间的不打滑最大节气门开度如表3所示。其中,0~16.3 km/h速度区间采用了估算的计算方法,因此无具体节气门开度信息。

图3 驱动力-最大附着力曲线
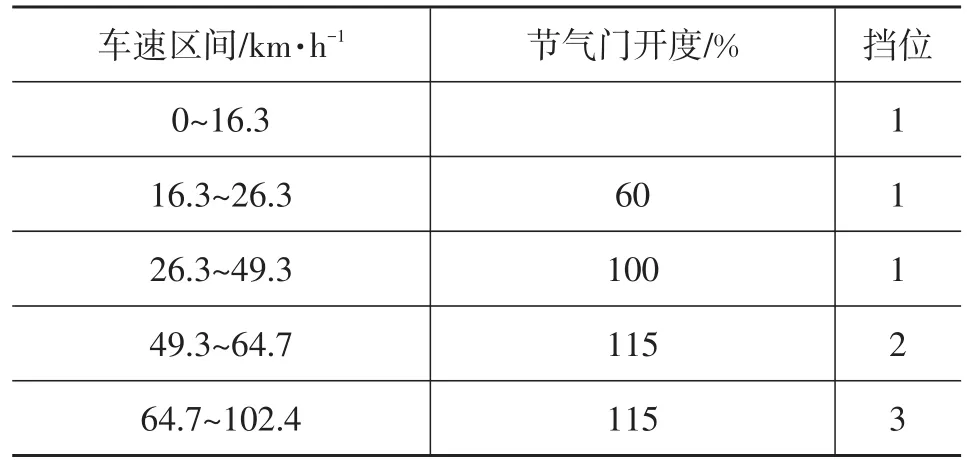
表3 车轮驱动下的节气门开度及挡位
图4所示为采用及未采用全动机翼两种工况下的最大附着力曲线。若不使用全动机翼,整个滑跑过程中机翼将始终保持正迎角状态,车速增加时驱动轮最大附着力不断下降,当最大附着力降至驱动力以下时车轮将发生打滑。由图4可知,在103 km/h时最大附着力已降至零,车轮为即将离地的完全打滑状态。使用全动机翼并将攻角设定为-11.2°以提供负升力,在车速为100 km/h时飞行汽车仍保持有7.2 kN驱动轮最大附着力,且随着车速的增加,最大附着力呈上升趋势。
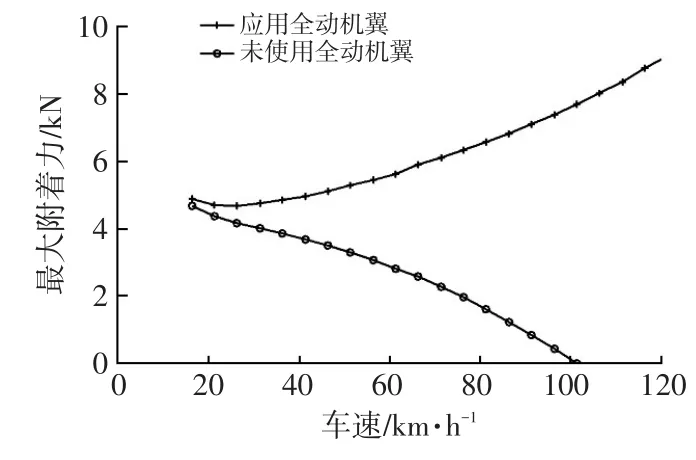
图4 最大附着力曲线
飞行汽车滑跑时需尽量使用最大节气门以缩短滑跑距离,按照该策略,对比图3提供的不打滑节气门开度情况,绘制车轮驱动力与螺旋桨推力如图5所示。由图5可知,车轮驱动力在滑跑期间始终高于螺旋桨推力,且在车速50 km/h附近车轮瞬时驱动力达到螺旋桨驱动力的2倍,说明车轮驱动可以提供更大的整车加速度,有利于降低滑跑距离。切换速度越接近起飞离地临界速度,采用车轮驱动的时间越长,滑跑距离缩短越明显。
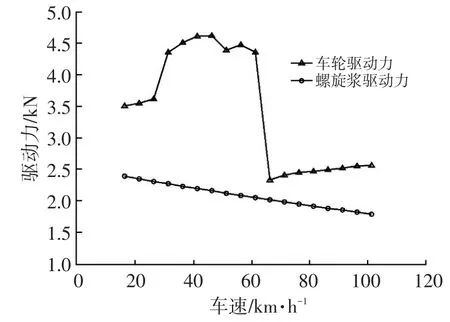
图5 车轮-螺旋桨推力曲线
4.5.4 滑跑距离对比
车轮-螺旋桨混合驱动、只采用螺旋桨驱动两种起飞滑跑方式的滑跑距离计算结果如表4所示。使用螺旋桨推进的起飞滑跑距离为230.9 m,而使用车轮驱动时该加速距离为174.5 m,距离缩短了24.4%。
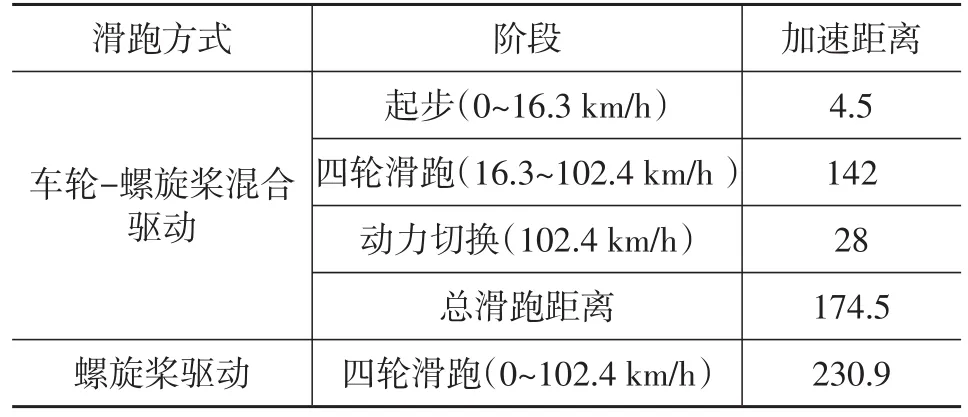
表4 两种滑跑方式的滑跑距离 m
5 结论
a.使用车轮-螺旋桨混合驱动的起飞滑跑方式可以获得更大的整车加速度,降低起飞滑跑距离。标志着动力切换阶段开始的切换速度越逼近起飞离地临界速度,滑跑距离缩短越明显。
b.由于需兼顾地面行驶与空中飞行两种工作状态,飞行汽车普遍选用功率较大的发动机。过剩的后备功率易造成地面行驶状态下的驱动轮打滑。在低速阶段,降低发动机节气门开度可避免打滑发生;在高速阶段,使用负攻角机翼可以提供足够的驱动轮附着力。
c.动力切换阶段的加速距离与切换时间密切相关,较短的切换时间有益于降低总滑跑距离。
