基于USB体制的卫星载波捕获防错锁方法
2018-11-21李俊瑶高海南
李俊瑶,高海南,冯 程,臧 进
(1.宇航动力学国家重点实验室,陕西 西安 710043;2.中国西安卫星测控中心,陕西 西安 710043)
0 引言
USB与扩频调制是现行航天测控领域的通用体制[1-2],地面测控设备与飞行器之间的信息交互主要包括遥控、遥测、测量和话音数据等,对其状态的正常提取与分析是控制飞行器稳定在轨运行的重要前提,也是掌握航天员生理状态的主要途径。当“搭载”在载波上的遥控副载波、遥测副载波等信号的调制度较大时,载波错锁(即接收机锁定在副载波上)的概率高达80%~90%[3]。一旦发生错锁,将导致跟踪信号丢失或遥测信号解调异常,需要进行人工判断并采取处理措施[4]。目前测控领域采用基于快速傅里叶变换的最大幅值判别法与对称判别法对防止载波错锁与假锁起到一定作用,但该方法对大调制度下副载波频谱幅度大的情况并不适用。文献[5]基于模拟调相信号相干解调输出信号的频谱特征实现了载波错锁频率引导的闭环控制,但是该方法需引入频率偏差的人工经验值。文献[6]采用快速傅里叶变换分段计算频段内信号频率,并与前次快速傅里叶变换(Fast Fourier Transform Algorithm,FFT)所得中心频率进行比对,根据误差信号是否满足阈值作为载波锁定判决条件,但当信号抖动较大或2次FFT分析均判定在错锁点时将造成误判。
本文在工程实践的基础上,建立了噪声干扰下的USB测控设备中频接收载波环模型,仿真分析大调制度下载波及副载波的时频特性,通过SVD降噪法对无线射频信号传输过程中引入的噪声误差进行降噪提取,克服了传统滤波器降噪、小波阈值降噪造成的信号失真、消噪效果不理想等问题;提出副载波解调法实现了副载波信号的抑制,有效提取载波信号,克服了大调制度下载波错误的问题,相较于目前使用的最大幅值判别法与对称判别法而言载波锁定效率及正确率更高。
1 载波捕获与载波错锁
1.1 中频接收模块工作原理
对于S频段的地面微波统一测控设备,USB测控体制通常采用载波调相。在载波捕获阶段,地面测控设备接收飞行器转发的下行射频载波信号后即刻进入载波捕获状态,信道下变频得到的中频输入信号进入基带接收机,经模数(A/D)转换后与本地产生的正交载波信号进行混频、滤波,输出的采样信号在DSP中进行FFT频谱分析与能量检测,得到载波频率即完成载波捕获。中频接收机载波捕获原理[7-8]如图1所示。

图1 接收机载波捕获原理
进入基带的中频载波信号包括由应答机转发的测距主侧音信号、一个次侧音信号、遥测信号及多普勒信息等,接收的基带信号经接收机再次变频至10.7 MHz二中频信号,与10.7 MHz本振信号混频,得中频调制载波信号表达式:
S中(t)=A·sin[2π(fc+fd)t+m主sinΩ主t+
m次sinΩ次t+mTMsinΩTMt],
(1)
式中,A为正弦调相波载波幅度;fc为载波频率;fd为载波携带的多普勒频率;m主,m次,mTM分别为主侧音、次侧音和遥测副载波调制度,一般为0.2 rad~1.5 rad。
1.2 载波错锁原因
目前载波防错锁措施主要利用载波频谱特性进行判断,但是简单地依靠频谱幅度或频谱对称性来进行判断对防止载波错锁与假锁的效果甚微[9]。根据工程实践经验得出载波错锁的主要原因如下:
① 空间环境、信道和设备元器件等引入的噪声干扰直接影响频谱质量,对载波频谱特性提取与判断造成影响;
② 当副载波调制指数较大,或调制的多种副载波在频带内产生交叉组合,可能造成载波频率模糊或载波幅度低于副载波的情况,从而引发误判;
③ 鉴相器的非线性特性使其输出的鉴相误差除零点外还存在其他极小值点[10],当鉴相器输出的相位误差恰好在这几个极小值点时,锁相环就会锁定在该错误频率点上;
④ 由快速傅里叶变换得到的频谱特性因采样点的影响会产生频率分辨率不高的问题,易受栅栏效应、频谱泄露的影响。
1.3 载波仿真模型建立
根据三角函数变换关系,式(1)可变为:
S中(t)=A·sin2π(fc+fd)t·cos(∑misinΩit)+
A·cos2π(fc+fd)t·sin(∑misinΩit),
(2)
式中,∑misinΩit=m主sinΩ主t+m次sinΩ次t+mTMsinΩTMt。
根据式(2)在Matlab/Simulink中建立接收中频信号的仿真模型,如图2所示。模型参数:A=2,Ω主=100 Hz,Ω次=2 Hz,ΩTM=65.536 Hz,fc+fd=400 Hz。

图2 载波仿真模型
对不同调制度下的载波模型进行仿真,得到图3所示时频结果。由图可知:① 副载波加调导致载波能量减小;② 各副载波信号在频带内存在交互影响,产生新的边频分量,并且该边频分量幅值随调制度的增大而不断变大;③ 当调制度为1.5 rad时,载波能量明显低于边频分量。可见传统的判对称法与能量最大法并不适用于大调制度下的载波信号捕获。
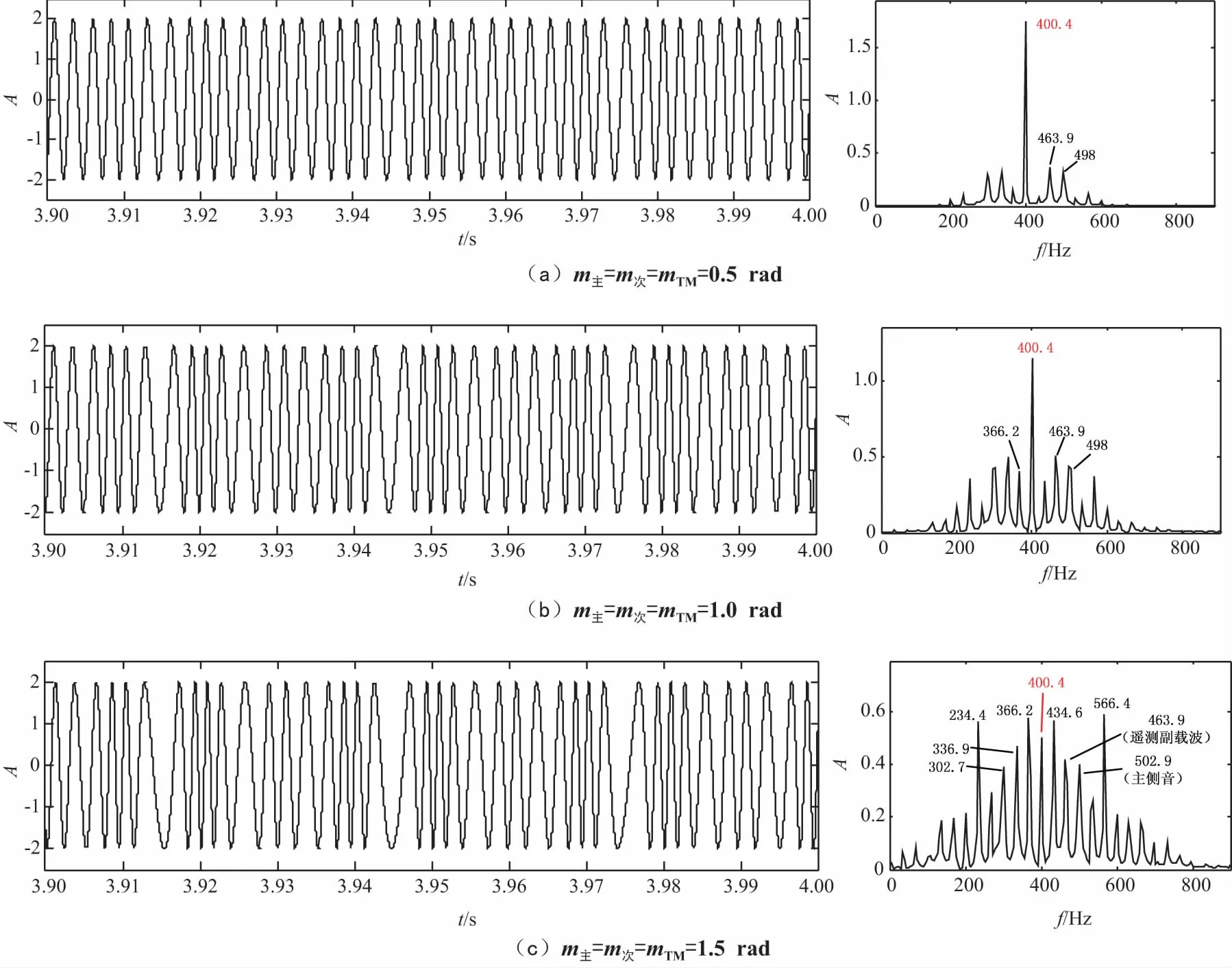
图3 不同调制度下载波时频特性
2 SVD降噪与特征提取
射频信号经大气空间在地面测控设备与飞行器之间远距离传输,会因自然界电磁波源(如闪电、宇宙噪声等)、信道器件和传输线等诸多因素引入噪声干扰。信号在进入地面接收机时需通过降噪处理提取出有用信号,避免在遥测、测量数据解算时产生影响。目前,测控设备采用传统滤波手段对信号进行低通或带通滤波,很容易将有用信号滤除或滤除噪声效率较低。本文结合Hankel矩阵与奇异值分解法能有效去除噪声干扰。
2.1 SVD分解去噪原理
奇异值分解(SVD)[11-12]是线性代数中一种重要的分解算法,在信号处理、统计学和数值分析等领域有重要的应用地位。奇异值分解去噪[13]的基本原理如图4所示。

图4 奇异值分解去噪基本原理
设含噪的原始信号x(t)=s(n)+v(n),其中s(n)为有用信号,v(n)为噪声信号,n=1,2……N(N为采样点数)。在线性代数中矩阵构造的方式很多,不同矩阵在SVD信号处理时效果不同[14-15]。经研究Hankel矩阵在SVD分解中能体现信号细节特征并反映信号主体骨架的近似组合,具有明显的优越性[16]。本文采用Hankel矩阵构造m×n阶矩阵X,其表达式如(3)所示,其中采样点数N满足约束条件N=m+n-1。
(3)
对矩阵X进行奇异值分解得X=USVT,其中U为m×m阶酉矩阵,V为n×n阶酉矩阵。

∑=diag(σ1,σ2…σk,…σr),σ1≥σ2≥…σk≥…≥σr>0即为矩阵的奇异值,它们反映了信号和噪声的能量集中情况。前k个较大的奇异值主要反应信号能量,构成有用信号矩阵Xs;后面较小的奇异值则反映噪声能量,构成噪声信号矩阵Xv。可见,只需将反映噪声的(r-k)个较小奇异值置零,然后进行矩阵重构即可得到降噪后的有用信号矩阵。
2.2 SVD降噪仿真分析
对某含噪的正弦信号进行SVD噪声抑制处理,选择1 000×501阶Hankel矩阵,输入信号信噪比SNRin=0 dB,得到图5所示仿真结果,可以看出,经SVD降噪后信号时域波形中的噪声得到了较好的抑制。

图5 SVD降噪时域仿真
对信噪比SNRin为-10 dB,-5 dB,0 dB,5 dB,10 dB时的输入信号分别进行100次仿真实验,得到如表1所示的SVD降噪性能指标结果。
表1 不同信噪比信号的SVD降噪性能指标

SNRin/dBSNRo/dBMSE-1014.147 50.019 2-516.569 20.011 0023.385 80.002 3527.183 99.562 7×10-41033.372 62.299 9×10-4
其中,SNRo为消噪信号的信噪比,该值越大表示信号去噪效果越好;MSE为消噪信号的均方误差,该值越小表示噪声抑制效果越好。可以看出,输入信号的信噪比越大则噪声滤除效果越好,信号的失真度越低。除此之外,将小波变换与SVD法结合用于信号降噪处理可以克服大矩阵运算导致时间过长的问题,有效提高了降噪效率[17]。
3 基于副载波解调的载波捕获
在USB模式下飞行器直接相干转发地面发射的上行射频信号,因此地面测控设备可利用副载波信号对基带中频接收机接收的中频调制载波进行解调,即式(1)经副载波解调得到式(4)所示结果。
S解调=S中(t)·sin(∑misinΩit)=
2m次sinΩ次t+2mTMsinΩTMt)-
cos(2π(fc+fd)t)]。
(4)
该解调信号主要包括两部分信息:一部分为改变调制度的调制载波信号,第二部分为单载波信号。根据信号处理知识可知,单载波信号的能量远高于调制载波信号能量,因此式(4)所示解调信号具有突出载频、抑制副载频的频域特性。对副载波调制度m主=m次=mTM=1.5 rad时的载波信号进行解调,得到如图6所示的频域仿真结果。由此可见,通过副载波解调实现了信号载波提取与捕获,降低了大调制度下的载波错锁概率。
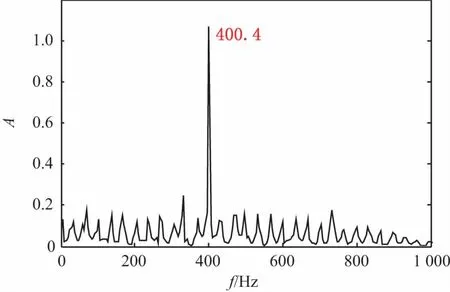
图6 解调信号频域特性
通过对USB体制下卫星载波中频环模型建立、时频域仿真分析,可得出以下结论:
① 随着副载波信号调制度的增大,调制载波信号的频域特性发生明显变化,副载频能量幅度逐渐增大,载频能量相应减小。当副载波调制度较大时,其频域特性不再具有显著的对称性与载频突出的特性,因此判对称法与能量最大法对载波捕获的判断效果不佳。
② SVD分解法相较于小波降噪、传统傅里叶变换降噪等方法具有原理简单、算法简便的特性,且对噪声抑制效果好,在信号处理中具有明显优势。
③ 经副载波解调后,中频接收信号实现了突出载频、抑制副载频的效果,从而增加了大调制度下的载波捕获概率,仿真结果验证了方法的有效性。
4 结束语
副载波解调法有效地克服了大调制度下因副载波能量高于载波能量而造成的载波错锁问题,SVD分解法能有效降低射频信号在传输过程中引入的噪声干扰,但是处理信号的长度受矩阵大小限制,矩阵阶数越小,所能处理的信号长度越短,而矩阵阶数越高,信号降噪处理时计算量增大,所需时间越长,该问题后续需进一步完善。
