论反例在中学数学教学中的作用——以贵州大学附属中学为例

黄新旭

（贵州大学明德学院 贵州贵阳 550000）

1 引言

在现实的学习及实践中，我们有如此的经历：当对某问题苦思而无果时，从反面切入，常能茅塞顿开，获得惊喜性的成功。又或，要否定一个命题，只要举出一个满足命题条件，而不满足命题结论的例子就行了。这在数学中称为举反例。G·波利亚说：“类比和反例是获得发明的伟大源泉。”在学习日常中，我们会总结出一系列的结论，而当结论是错误的，那么举出反例就可以推翻。

同样，在中学数学教学中，某些数学知识学生仅从正面去思考会很模糊，然构建适当的反例常能收到出乎意料的甜果，学生既深刻地理解了知识，又培养优良的数学品质。故，仅靠正面示范，没有反例的参照，无法凸显知识的本真，对知识的理解就会失真。

2 反例的概念

数学中的反例，是指符合命题的条件，而又不符合该命题结论的例子。简称，反例就是一个指出某命题不成立的例子。从广义上来讲，所有的例子都可称为反例，因为它总可以推出某命题不成立。反例教学是指在概念、定理等教学过程中，教师有针对地构建看起来正确而实质完全错误的解答，进一步巧妙地引领学生发现、顿悟、归纳出错误，最终得出正确结论的教学方法。

精准说来，反例教学法中的反例是指教师在教学实践中，收集的典型例题的典型误解、重要知识点的典型错误认识。然而，如果反例庞杂，则学生反而会被引入歧途，倘若是教师信手拈来的反例，那么其意义就很微小，因此，反例必须具体有典型性、精准性、简炼性。

3 运用反例的调研

贵州大学附属中学始建于1947年，目前是一所全日制封闭精细管理的贵州省属中学，含有初高中数学教师24名。通过对这24名教师进行问卷调查得出以下结论：

表1

表2

表3

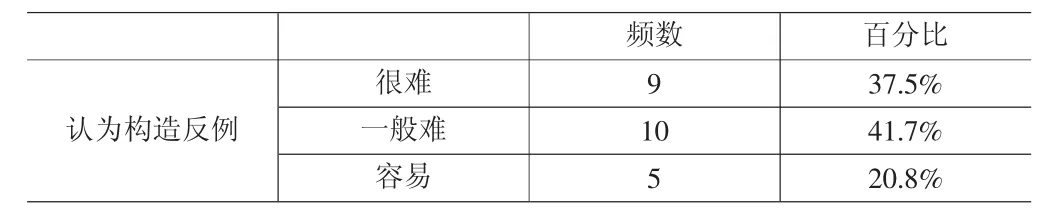
表4

4 目前数学反例使用存在的主要问题

①新课标对反例没有具体要求，关于反例的考题基本没有；②教师认为反例的作用微乎其微缺乏运用反例的意识；③教师对反例的了解甚少，无法有效的把反例运用于教学中；④教师构造反例的能力低，不能系统地教给学生构造反例的方法；⑤关于反例的资料缺乏，获取反例的渠道单一，主要从教材及教材参考书和自己的经验获取；⑥大部分的教师都是在平时教学过程中少量的穿插使用反例。

5 反例在数学教学中的作用

5.1 反例可以加深学生对数学概念及原理的理解

教学中，概念、定理、公式一般采用正面阐述的形式，学生往往对一些关键性词句、条件理解不透彻，看不到本质，只是机械地强记。如果遇到名称相似或结构相类似的知识点，就会混淆得一塌糊涂。

例1：不少学生片面地认为函数就是：一个变量随着另一个变量的变化而变化，它们就是函数关系，可提出这两个例子：

（1）人的体重与年龄成函数关系吗？

（2）若 y=cotx·tanx，则 y是 x的函数吗？

解析：①学生认为体重随年龄的增加而增加，因而构成函数关系。实际上，年龄无法确定体重，即当年龄发生变化时，体重没有确定的值和它对应，故不符合函数的定义。②学生认为y=cotx·tanx=1，故y不是x的函数。实际上对每一个定义域内的x值，y总有唯一确定的值（y=1）和它对应，只不过y的值始终不变罢了，因此是函数。

5.2 反例是一种纠正错误的常用办法

反例之所以被称为反例，是因为纠错是它最凸显的也是最根本的作用。讲授习题上，举反例是反驳与纠正错误的有效方法，是学生加强学习的有力武器。面对学生解题中所出现的共性错解，教师可以示以反例，曲中窥直，用反例说明解法有误，从而引导学生去找到错误的根源，最终让师生共同品尝成功的“蛋糕”。

例2：若a=A，b=B，则a+b=A+B，反之是否成立？

解析：反之不成立。显然直接说明不好入手，借助反例：若a=6，b=4，则 a+b=10，若 A=2，B=8，则 A+B=10，但是 a≠A，b≠B。

5.3 借助反例可以引导学生发现问题

课本中的例题所提供的解题思路清楚明确，学生只需机械记忆与模仿，长此以往会使学生缺乏勇于探索、质疑的能力。为了补缺，在例题讲授中教师设置适当反例，故意制造陷阱，让学生透过现象，看到问题的本质，养成善于发现的品质。例如在讲授分式方程的解法时，书本都是给出解方程的规范步骤，而照本宣科的教学不易发现问题，同时学生也懒得去探索、发现。巧用反例，可以使学生发现漏洞，自主发现，获得正确的结论。

解：方程两边同乘以x-1，得：

-3+4（x-1）=1，

解之得x=2，

经检验知x=2是原方程的解。

面对这样的反例，学生的兴趣就提上来了，一眼就能发现错误的原因是去分母时方程右边漏乘了（x-1）。通过这个反例，加深了学生去分母不要漏乘的印象。

5.4 反例可以培养学生思维的多重维度

数学学习的任务就是要培养学生的逻辑思维能力，从而正确地解答数学问题，并能优化其他问题的解决。新课标明确指出：“发展思维能力是培养能力的核心。”思维的缜密性、灵活性、发散性、深刻性、创新性都是思维重要的品质。根据中学生的心理特点和学科自身的特点，运用反例培养这些思维品质是一个行之有效的方法。设置巧妙的反例，能让学生学会多维度考虑问题，灵活思维。然而，构造反例的方法并不是唯一的，需要学生对所学知识有透彻的理解，充分挖掘数学功底，展开想象，故构造反例的过程也是学生发散思维和创新思维的训练过程。

例4：带根号的数都是无理数。

5.5 反例可以极速解题的速度

反例的学习和运用可以提高我们的数学能力，优化解题过程，并在日积月累中提高解题速度。反例教学实际上是教师为了清晰学生在掌握数学知识过程中的模糊印象，乱套公式等毛病所挖的坑。通过正反对比，构造极端的反差，使学生对错误留下极为深刻印象，从而，降低再犯类似的错误的几率，最终使学生对所学知识得到进一步巩固升华。

例5：在学习反比例时可举出反例：倩倩总共要背18首诗，问已经背的和没背的数是否成反比例？

解析：“对的”，显然这些学生没有充分掌握成反比例的条件：两个量的乘积为定植。这个题是两个量的和一定，学生顿时豁然开朗。

5.6 反例是鉴别假命题简易的方法

反例是否定一个命题的绝佳手段。在学习过程中，学生通过类比或归纳等方法得到一些看似正确实则错误的结论，要否定它，反例是一种行之有效的利器。判断一句话（或一个结论）的真伪，首当其充的方法就是构造反例。这是由反例本身的特性决定的，在澄清是非，揭示黑白，否定命题时它具有直观、简明、说服力强等特点。

例6：负数就是在一个数的前面加一个负号。

解析：许多理解不清的学生认为是对的，只要亮出反例，如果是负数，在它的前面加一个负号就变成了一个正数了。再如果是0，在0的前面加个负号还是0。

5.7 教学相长的助推

教学包含教师的教与学生的学两部分。教学离不开教师和学生这两个相对主体，在教学中，教师不仅是讲授者和组织者，也是参与讨论的一位，学生的思维“动”起来后，他们在研究问题的广度和深度上可能会超越教师，使教师和学生之间能相互学习。反例在教学中虽处于次要地位或辅助教学地位，但它是培养学生主动性和能力的一种途径，它有利于教师更有效地教授知识，也有利于学生更好地掌握数学各类知识，达到双赢的局面。

例7：两个无理数的和是否一定是无理数？

6 结束语

在中学数学教学中，适时地引入一些反例或启发学生构建反例，往往能使学生在认识上产生质的飞跃，有助于他们掌握并能灵活运用。教师根据学习过程中学生容易出错的地方，开展反例教学，讲解精选的反例，往往能引起学生内心的共鸣，增加学生学习的热情，使认识与体验相融合，打破对数学的惯性思维：“枯燥、繁琐、难如登天”，激励其上进的欲望，并形成学好数学的坚定信念，痴于与数学谈一场永不分手的恋爱。