捕食者具有Allee效应的Lotka-Volterra捕食-食饵系统稳定性注记
2018-11-19陈凤德关心宇黄小燕
陈凤德,关心宇,邓 行,黄小燕
(福州大学 数学与计算机科学学院,福州 福建 350016)
1 问题引入
一段时间以来,具有Allee效应的捕食-食饵模型动力学行为研究引起了学者们的高度重视,见文[1-4]以及所引文献。Hüseyin Merdan提出了如下食饵具有Allee效应的Lotka-Volterra捕食-食饵模型[1]:
(1.1)
其中β是正常数,刻画了Allee效应的大小。Merdan的研究表明如果r-aβ>0成立,则系统具有唯一的局部渐近稳定的正平衡点,作者的数值模拟表明Allee效应会使得系统要用更多的时间达到它的稳定态。
受Hüseyin Merdan启发,Xinyu Guan等提出如下捕食者具有Allee效应的Lotka-Volterra捕食-食饵系统[2]:
(1.2)
其中r,a和β均为正常数,β刻画了Allee效应的大小。作者证明了如果r>a,则系统是持久的,由此知两个边界平衡点是不稳定的,借助这一事实和Dulac判别法,作者们最终证得了系统的唯一的正平衡点是全局稳定的。然而,文[2]的分析手法并不能适用于r≤a的情形,而作者也没对r≤a进行任何的分析。现考虑如下例子:
例1:
(1.3)
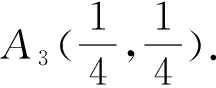
数值模拟(图1)表明此时正平衡点A3是全局渐近稳定的。
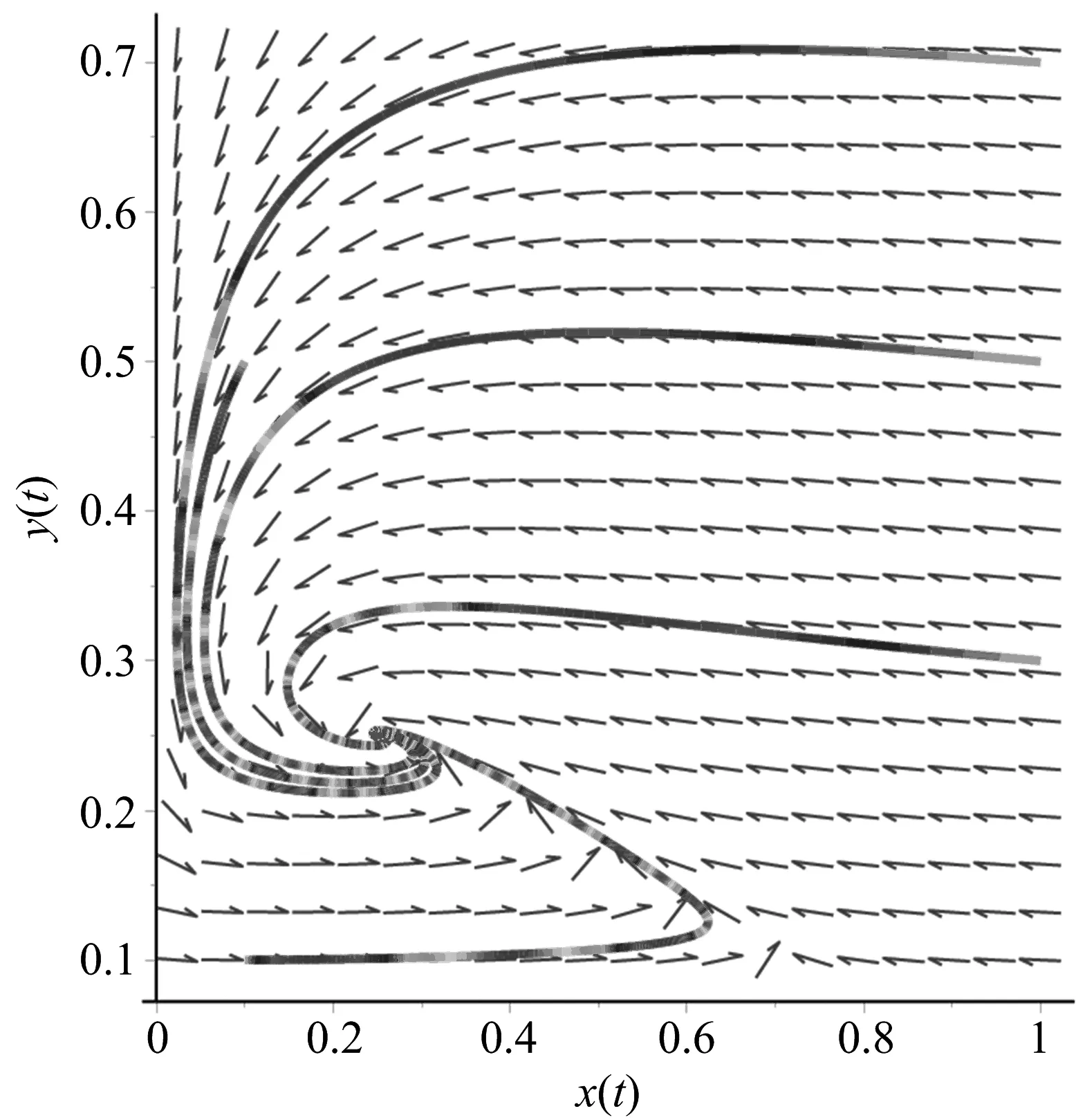
图1 系统(1.3)的具有初值(x(0),y(0))=(0.1,0.5),(0.1,0.1),(1,0.3),(1,0.7)和(1,0.5)的解的动力学行为
数值模拟启发我们提出如下猜想:
猜想:对r≤a的情形,系统(1.2)也有唯一的全局吸引的正平衡点。
本文的目的在于给出上述猜想的严格证明,我们将会在下一节中证明这一猜想。
2 主要结果
系统(1.2)的平衡点由如下方程组所决定
(2.1)
计算易知系统(1.2)有如下三个平衡点:A0(0,0),A1(1,0)和A2(x*,y*),其中
(2.2)
有关上述三个平衡点的局部稳定性态,我们有如下结果:
定理2.1A0(0,0)是鞍点,A1(1,0)是鞍结点,相应的,这2个平衡点都是不稳定的;A2(x*,y*)是渐近稳定的。
有关上述三个平衡点的全局稳定性态,我们有如下结果:
定理2.2系统(1.2)的唯一的正平衡点A2(x*,y*)是全局稳定的。
定理2.1的证明:计算可知系统(1.2)的雅各比矩阵为
(2.3)
其中
由此可知在平衡点A0(0,0)处的雅各比矩阵为
(2.4)
这表明A0是非双曲的,从而A0的稳定性不能由雅各比矩阵直接进行判断。为了探讨A0的稳定性态,首先,做变换t=rτ,则系统(1.2)变为
(2.5)
其次,做变换X=y,Y=x,则系统(2.5)变为
(2.6)
对系统(2.6)在(0,0)点泰勒展开,且为简便计,用x,y,t表示X,Y,τ,则有:
(2.7)
其中
这里P6(x,y)是形如xiyj的项组成的多项式,其中i+j≥6.由y+Q2(x,y)=0可解得隐函数y=0=φ(x),将其代入P2(x,y)可得
(2.10)
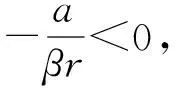
下面考虑平衡点A1(1,0),系统(1.2)在平衡点A1(1,0)的雅各比矩阵为
(2.11)
(2.11)表明A1也是非双曲的。相应的,A1的稳定性也无法从雅各比矩阵来判定。为了探讨A1的稳定性,我们首先做一变换,将A1移至原点(X,Y)=(x-1,y),其后在原点按照泰勒展式展开,则系统(1.2)变为:
(2.12)
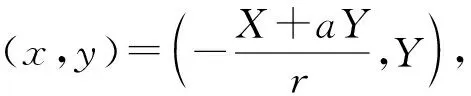
(2.13)
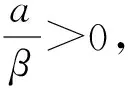
Guan等已经证明了系统(1.2)的正平衡点A2(x*,y*)是局部渐近稳定的[2]。
定理2.1证明完毕。
注:文[2]中作者已经证明了在r>a时,边界平衡点A0(0,0)和A1(1,0)是不稳定的。本文中,我们借助新的分析手法,表明文[2]的限制r>a是多余的。
定理2.2的证明:注意到A0(0,0)和A1(1,0)都是不稳定的,仅有A2(x*,y*)是局部稳定的,完全类似于文[2]中定理3.1的证明,借助Dulac判别法,我们可证得系统(1.2)不存在极限环,由此,可知唯一的正平衡点是全局稳定的,定理2.2证毕。
3 讨论
Hüseyin Merdan提出了食饵具有Allee效应的Lotka-Volterra捕食-食饵模型[1],作者探讨了模型正平衡点局部稳定性。Guan等受文[1]影响[2],提出了捕食者具有Allee效应的Lotka-Volterra捕食-食饵模型,作者们在条件r>a下证明了系统有唯一的全局稳定的正平衡点,但是,对r≤a情形,作者们并未进行探讨。本文中,我们证明了对r≤a情形,系统(1.2)一样有唯一的全局稳定的正平衡点。我们的结果补充和完善了文[2]的结果。由定理2.2可知:在系统(1.2)中,捕食者种群的Allee效应不会影响系统的最终平衡密度。
