时间序列模型在汽车拥有量预测中的应用

彭妍 陈珊

摘要：本文运用了时间序列模型，对原始序列{s}进行取对数、二阶差分处理，根据处理后平稳序列的自相关系数图和偏自相关系数图，经分析最终选择了ARIMA（2，2，3）模型为最合适的预测方法，因此进一步对2018年的汽车拥有量做出预测研究。

关键词：时间序列模型 ARIMA 汽车拥有量

一、引言

2017年我国已经连续九年汽车销量全球第一，我国汽车保有量逐年高升，北京、杭州、成都等一线城市已实行限行限号制度以控制道路的交通流量，从现有数据来看，人们对车辆的需求日益增多，拥堵现象不再是大城市的问题，不断加重的拥堵现象也在向中小城市蔓延。根据汽车化程度与人均居民收入存在递增关系可知，随着人均可支配收入的逐年增加，生活条件的大幅度提升，未来汽车保有量会不断增加，即便是很适合宜居的二三线城市，也会被交通拥堵所困扰，因此为了对城市道路的规划提供有利的参考，预测我国汽车拥有量是十分必要的。本文引入时间序列模型，从中国统计年鉴选取我国1990-2016年的私人汽车拥有量作为原始序列{s}的数据，以年为时间单位，对2017-2018年的汽车拥有量进行了一个预测。

二、平稳化处理

从原始序列{s}的时序图中可以看出我国私人汽车拥有量有明显的上升趋势，显然原始序列{s}是非平稳的，为了能够对序列进行后续的预测分析，要使其平稳化，本文选择两种方法：取对数法和差分法。将取对数后的数据进行一阶差分，并做出差分处理后序列的时序图：

从图中可以看出，这一序列值未在零均值附近随机波动，因此认为一阶差分后的序列仍是非平稳的，再次对序列进行差分处理，得到二阶差分后序列的自相关、偏自相关图和时序图如下：

本文将取对数后的序列进行二阶差分，自相关系数图和偏自相关系数图都具有快速趋向于O的特征，且时序图中的数据均在0数值附近并以一定的范围为界随机波动，因此可认为In{s}（拥有量）序列是二阶单整序列，即In{s}（拥有量）～I（2）。（为进一步验证其平稳性可做DF或AD检验即F单位根检验。）

三、模型的建立

综上分析，本文建立ARIMA（p，2，q）（0，0，0）模型，根据序列的自相关系数和偏自相关系数这两个统计量来识别ARMA（p，q）模型，二阶差分后的序列的自相关系数在滞后四期呈衰减趋于零，表现为拖尾性，在偏自相关系数图中，滞后三期的偏自相关系数显著不为零，但之后逐渐衰减趋于零，具有ARMA的特征。分析得出p，q可以取数字1、2、3，本文以MAPE、MaxAPE、BIC较小，平稳的R方较大为标准选择最好的模型，通过对比最终选择ARIMA（2，2，3）模型。

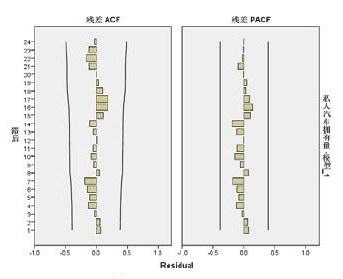
对建立的ARIMA（2，2，3）模型进行检验，即对其残差序列做是否为白噪声序列的分析，从图中可以看出残差序列的自相关系数、偏自相关系数都均匀的分布在置信区间内并趋向于0，表明残差序列通过白噪声检验，也可认为序列{s}适合利用ARIMA（2，2，3）模型进行后续预测。

五、模型的预测

在做最终预测之前先利用ARIMA（2，2，3）模型对2015-2016年的数据做预测分析，以检验拟合效果及考虑误差的范围，由于MAPE=3.066，选取模型预测误差大致控制在3%左右，可认为选取的最优的模型视为短期内有较高的精度，2015-2016年的预测结果和真实结果拟合度很好，因此将样本扩展到2018年，利用ARIMA（2，2，3）模型對汽车拥有量进行预测

六、结语

从分析和预测的结果中可看出，取对数和适当的差分对数据，选择适当较低的模型阶数，可得到较为理想的理论结果：2018年的全国私人汽车拥有量将达到23570万辆。但由于时间序列模型的选择较多且带有一定的主观性，本文进行处理时原数据较少且仅对历史数据进行建模分析，对预测精度是一个不利的影响，汽车拥有量的预测没有考虑到市场中的一些因素：第一，受小排量汽车购置税优惠政策取消、新能源补贴政策调整未确定等政策因素影响；第二，随着经济发展、生活水平的提高、一带一路倡议的持续推进以及国际市场的进一步复苏，促进了汽车拥有量的增加；第三，共享汽车的发展，处于推动及抑制新车销售转换期，在2018年，若共享汽车能够像共享单车一样提高了人们的生活便捷程度，私人汽车的销售将受到巨大的挫折。第四，二手车交易增长对新车销售的双重影响。因此还需要考虑更多的因素且增加样本，有待建立更优的模型，提高预测精度。