25 m射电望远镜俯仰系统的全过程建模*

张洁钰， 保 宏

(西安电子科技大学电子装备结构设计教育部重点实验室, 陕西 西安 710071)

引 言

随着深空探测对射电望远镜的探测范围以及精度要求的提高，大型化成为射电望远镜发展的趋势。然而，结构大型化必使其固有频率降低，柔性增加，从而给保障天线高指向精度带来困难[1]。当前，最优控制成为有效保障大口径天线高指向精度的控制算法，其主要特点是伺服性能好，抑制干扰能力强[2-3]，但其控制器设计需要较为精确的被控对象模型。因此，大口径射电望远镜的精确建模成为实现最优控制算法的先决条件。

对于小口径天线，传统建模方法是将其等效为刚性。文献[4]采用堆聚质量法建立天线系统动力学分析模型后，基于拉格朗日方程建立了其动力学方程。

随着天线口径增大，柔性增加，传统建模方法难以输出柔性运动，因而已不适用。当前已有学者对大口径天线的建模进行了研究。文献[5]讨论了天线驱动系统的模型；文献[6]考虑风荷对结构输入的影响，建立了动力学方程；文献[7]研究分析了上海65 m射电望远镜在太阳辐射作用下的非均匀温度场。但文献[6-7]中的风荷和温度主要影响电性能，对伺服系统中的控制起不到作用。文献[8]利用系统辨识思想构建了伽利略望远镜模型，但该方法是在已有实物的基础上，通过采集实验的输入输出数据进行建模，因此只能用于已有天线实物模型后期的研究，在天线设计阶段无法提供帮助。文献[9]根据有限元模型建立了GBT伺服系统的模型。文献[10-12]介绍了射电望远镜的有限元模型，随后根据有限元模型建立了用于DSS13俯仰指向的状态空间控制系统模型，然后将此方法扩展到方位，建立了全控系统模型。但该方法只考虑了大齿轮的影响因素，未考虑副面在整个射电望远镜指向精度中的影响。

由于大射电望远镜结构复杂，模态众多，不便于系统全过程建模以及后期的最优控制，因此需要对模态进行合理缩聚，得到能真实反映复杂系统动力学特性的简化模型。常见的模态缩聚的方法有3种：1) 模态有效参数判别法[13]，根据前n阶模态的有效质量分数和进行模态截断。由于它能降阶的阶数是有限的，一般只适用于建模的初期。2) 模态能量法[14]，以能量响应信息的收敛程度来进行模态截断。3) 传递函数范数法[15-16]。该方法本质上是能量法，通过各阶模态对系统输出能量的贡献进行模态选取。它可以得到各阶模态对应的范数指标，不仅能应用于模态截断，也能应用于模态选取。经综合考虑，本文采用传递函数范数法对25 m口径射电望远镜进行模态缩聚。

本文基于Gawronski的建模思想，依据25 m射电望远镜的有限元模型，建立了由电机到大齿轮和主反射面直至副面的全过程模型。

1 问题提出

大射电望远镜的俯仰运动过程为：电机通过减速器带动大齿轮和主反射面转动，副面撑杆和副面则跟随其一起转动。该俯仰运动的目的在于从特定指向角度接收所需电磁波，电磁波经主反射面反射到副面，由副面收集信号进入接收机来分析信号，所以高指向精度与伺服控制过程密切相关。图1为25 m射电望远镜的反射体的有限元模型。该模型由14 619个梁单元、12 156个壳单元、449个质量单元和20 627个节点组成，结构复杂，柔性因素较大，严重影响主副面的伺服控制。传统伺服控制方法无法解决该问题，所以采用最优控制，但其控制器设计需要较为精确的被控对象模型。而传统建模方法难以正确反映实际运动，也无法输出各关键部位的工作过程，而且现有模型都不含副面撑杆和副面这个柔性最强的环节。因此，建立一个能够模拟整体俯仰运动和各部分实际运转状况的模型成为亟待解决的关键问题。基于此，本文提出了全过程建模。

图1 反射体有限元模型

2 全过程建模

射电望远镜在俯仰运动过程中，首先由电机产生输入力矩τm，经减速器放大，获得大齿轮和主反射面的输入力矩τ。电机和减速器的动力学方程计算为

(1)

2.1 大齿轮和主反射面建模

使用如下的状态空间方程来建立大齿轮和主反射面的控制模型：

(2)

2.1.1 柔性部分建模

为了使结构可以在俯仰方向自由旋转，施加的约束条件如图2所示。释放俯仰轴两端点16740和17026绕俯仰轴旋转的自由度，约束其他剩余自由度；约束大小齿轮啮合点16244沿大齿轮边缘切向的自由度。

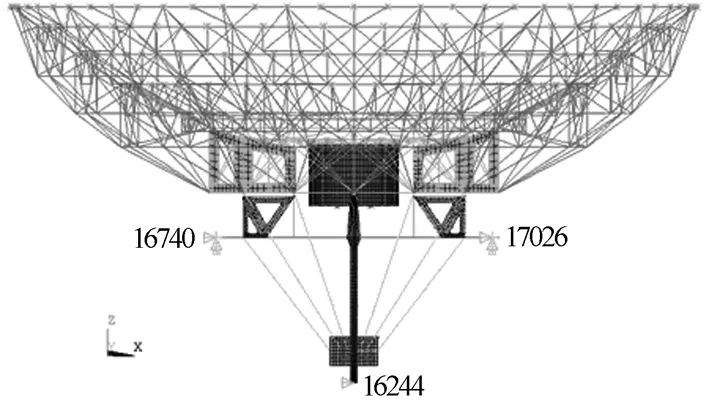
图2 大齿轮和主反射面的约束图

通过ANSYS模态分析，可获得大齿轮和主反射面的各阶固有频率ωi和模态振型Φ。由于第1阶为刚性模态(固有频率和模态位移均为0)，在此处计算柔性模态，所以i= 2, 3,…,n。

模态矩阵的规模与结构有限元的节点数量和选取的模态阶数相关。当节点数量和选取的模态阶数过多时，模态矩阵的规模将呈爆炸性增加，给相关参数的进一步计算带来困难。因此，本文选取少量的节点，配以合适数量的模态振型构建模态矩阵。如图3所示，选取了n1、n2和n33点，其中，n1为俯仰大齿轮和小齿轮的啮合点，n2为大齿轮的中心点，n3为大齿轮z方向上与n2相距为l的一点，α为啮合点切向方向与方位轴的夹角,Fn1为啮合点处切向方向的作用力，Fn1y和Fn1z为Fn1在y轴和z轴上的分量，r为小齿轮半径。

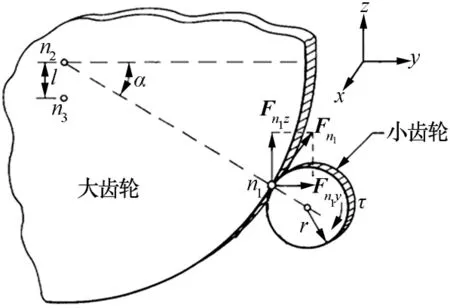
图3 大小齿轮啮合图

因此，模态矩阵Φ=[Φn3Φn1Φn2]T。其中：

Φn2和Φn3的表达式与Φn1类似。

假设结构的模态阻尼系数ζi= 0.005，则Ami[11]为

(3)

大齿轮和主反射面的输入力矩为τ，小齿轮半径为r，则Fn1为

Fn1=τ/r=[Fn1xFn1yFn1z]T=

[0r-1sinαr-1cosα]Tτ=Bn1τ

(4)

式中，Fn1x为Fn1在x轴上的分量。

所以整个射电望远镜结构的输入矩阵B0为

B0=[0Bn10]T

(5)

将输入矩阵B0转化成模态输入矩阵bm得：

(6)

式中，Mm为从ANSYS提取的模态质量矩阵。

因此输入矩阵Bmi为

(i=2,3,…,n)

(7)

俯仰角θe为

(8)

式中：Φn3y=[φ2n3yφ3n3y…φin3y…φnn3y]；Φn2y=[φ2n2yφ3n2y…φin2y…φnn2y]。

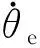
(9)

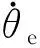
(10)

对应的输出矩阵Cmi为

(11)

2.1.2 刚性部分建模

刚性部分的计算方程为

(12)

(13)

2.1.3 刚柔结合

Am=diag(Ami) (i=1,2,…,n)
Bm=[Bm1Bm2…Bmn]T
Cm=[Cm1Cm2…Cmn]

(14)

式中：Am1、Bm1和Cm1代表大齿轮和主反射面结构的刚性部分；Am2…Amn、Bm2…Bmn和Cm2…Cmn代表结构的柔性部分。

若要单独输出实际转角，则对应的输出矩阵为Cma；若要单独输出实际角速度，则对应的输出矩阵为Cmb。

2.2 副面撑杆和副面建模

EIy(4)=0

(15)

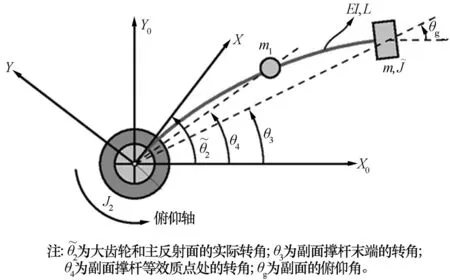
图4 副面撑杆和副面的等效结构示意图

柔性梁被分为2段，分别对其进行4次积分后得：

(16)

式中：y1(x)为第1段梁；y2(x)为第2段梁。

在满足连续性：

y1(0)=0
y1′(0)=0
y1(L/2)=y2(L/2)
y1′(L/2)=y2′(L/2)
y1″(L/2)=y2″(L/2)

(17)

几何条件：

(18)

动力学条件：

(19)

的前提下，可得状态空间方程：

(20)

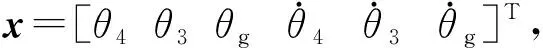
(21)

C3=[I3×303×3]

此时，反馈力矩为

(22)

最终可得电机到大齿轮和主反射面直至副面的全过程模型，即式(1)、(14)和(21)。

3 简化模型

上述模型均为全尺寸状态空间方程，经分析可知，方程参数过多，维数过大，控制困难，因此本部分对上述模型进行简化：首先，对大齿轮和主反射面模型进行模态选取，从而实现结构的模型缩聚；其次，对副面撑杆和副面模型进行简化，通过忽略副面撑杆质量以及副面俯仰转动惯量，实现结构模型简化[18]。

3.1 大齿轮和主反射面的模型缩聚

利用Ami、Bmi和Cmi可计算出各阶模态对应的传递函数的H2范数的平方[15-16]：

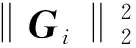
(23)

基于此，得到模态缩聚范数图，如图5所示。

图5 模态缩聚范数图

由图5中的前n阶范数的比重可看出，前50阶所占比重接近于1，所以提取前50阶模态。

已知H2范数可用来检测每个状态变量的能控性和能观性，因此可删除具有极小H2范数的模态，因为它们是弱能控和弱能观的，引起的建模误差可忽略。考虑到刚性模态(第1阶模态)是必须保留的，这里只对柔性模态(第2～50阶模态)进行选取。根据‖Gi‖2的大小对状态变量重新排序：新的第1阶模态对应的范数值最大，最后一阶模态对应的范数值最小。根据缩减相对误差，可删除后面的模态，找出剩余模态排序前的对应位置。

取缩减相对误差≤0.01，由图5中的各阶范数可知，保留的柔性模态为第10阶和第12阶。此时，可将式(14)简化为

Am=diag(Am1,Am10,Am12)
Bm=[Bm1Bm10Bm12]T
Cm=[Cm1Cm10Cm12]

(24)

3.2 副面撑杆和副面的模型简化

(25)

(26)

该模型的主要特点是模拟副面变化的影响非常简单。此时，反馈力矩为

τ3=K2(θ2-θ3)

(27)

最终可得电机到大齿轮和主反射面直至副面的缩减后的全过程模型，即式(1)、(24)和(26)，可以直接用于控制器的设计。

4 仿真分析

利用上面建模得到的状态空间方程，搭建Simulink框图，如图6所示。仿真过程中需要用到的一些参数分别在表1、表2和表3中列出。

图6 俯仰力传递路径框图

参数数值Jm/(kg·m2)0.4Km/(V·s·rad-1)1.36Kt/(N·m·A-1)1.23K1/(N·m·rad-1)4.958e9Rm/Ω0.223Lm/H0.003 65N36 000

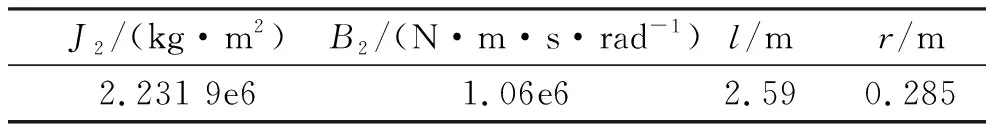
表2 大齿轮和主反射面参数

注：表中B2为粘滞摩擦系数。

表3 副面撑杆和副反射面参数

查阅电机表，当额定电压为440 V时，对应的额定转速为3 090 r/min，即323.58 rad/s。设计时未考虑放大器环节，所以直接输入440 V的电压。电机经过减速比为 36 000的减速箱后，角速度减小为0.009 rad/s。

图7为大齿轮实际角速度。由图7可以看出，大齿轮的实际角速度在0.009rad/s附近波动，波动范围为0.008 9～0.009 1 rad/s，这是考虑了柔性因素的缘故。

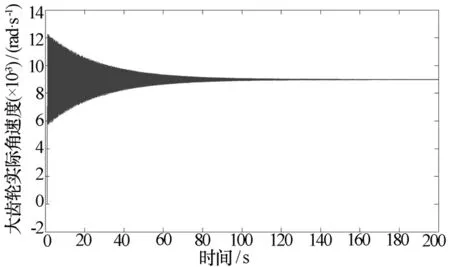
图7 输出角速度

图8为副面顶端角速度。从图8可以看出，副面顶端角速度在0.009 rad/s附近波动，波动范围为0.008 6～ 0.009 4 rad/s。很显然，副面顶端角速度相对大齿轮实际角速度更大，符合副面撑腿相对大齿轮更柔的特点，所以符合实际情况。

图8 副面顶端角速度

图9为副面撑杆和副面对大齿轮和主反射面端的反馈力矩。从图9可以看出，该方法可以直接输出中间环节的值，突出了它的优点。

图9 反馈力矩

5 结束语

本文依据25 m射电望远镜的有限元模型，建立了俯仰系统从电机到副面运动的全过程模型，并对模型进行了简化，使其能直接用于最优控制器设计，提高射电望远镜的指向精度。将射电望远镜整体运动过程分为电机到大齿轮和主反射面、大齿轮和主反射面到副面2部分并分别建模，其优点在于：1)不受限于实物模型，在天线设计阶段就可模拟各部分的实际运转状况；2)能准确模拟射电望远镜的整体俯仰运动，体现结构的各部分特性，不仅可以得到副面顶端的速度，还可以得到中间环节值，如扭矩、电流、大齿轮速度等。仿真验证表明该建模方法是可行的。下一步将通过现场实验进一步验证该方法的可靠性与准确性。