分数阶控制器在光电吊舱控制中的应用
2018-11-16
长春理工大学 电子信息工程学院,吉林长春 130022
一、引言
20世纪80年代,基于各种复杂系统研究基础之上,分数阶微积分在控制领域的应用受到研究者关注[1]。目前工业控制系统中大多采用传统的PID控制器,分数阶PIλDμ是传统PID的一般性,因其多了两个参数λ、μ,其过程更细腻、更具有灵活性,分数阶PIλDμ控制器比整数阶PID控制器有更好的控制品质、动态特性和更强的鲁棒性[2]。
在实际控制系统中,常常会伴有强干扰和噪声的影响,1960年卡尔曼(Kalman)提出了卡尔曼滤波理论,把状态空间概念引入估计理论中,采用时域上的递推算法在数字计算机上进行数据滤波处理,卡尔曼滤波在控制领域得到广泛应用[3]。
本文首先运用MatLab软件中可视化系统辨识工具箱模块对光电吊舱俯仰环进行数学模型参数辨识,在不考虑扰动条件下对系统模型设计分数阶控制器进行仿真分析,通过改变系统增益大小分析对比得出,采用分数阶控制器控制,系统具有较强的增益鲁棒性。实际控制系统中常伴有扰动和噪声,单纯的分数阶控制器无法抑制扰动的影响,在分数阶控制器基础上加入卡尔曼滤波器对噪声进行滤除,仿真结果显示,卡尔曼滤波器与分数阶控制器结合对吊舱系统控制,可以有效滤除噪声,增强系统鲁棒性和抗干扰能力。因此,对分数阶控制器和卡尔曼滤波器的理论与应用研究有重要意义。
二、分数阶微积分及分数阶控制器
1、分数阶微积分理论
分数阶微积分主要研究任意阶次的微分、积分算子的特性及其应用。其一般分数阶表达式为:

t1—微积分的上限;
t0—微积分的下限;
α—实数或复数;
Re(α)—复数α的实部。
对于分数阶微积分的定义,不同的数学家给出不同定义,在实际控制系统应用中,Caputo分数阶微积分定义更适合分数阶微积分初始值问题的求解[4]。
2、分数阶控制器
分数阶控制系统采用分数阶微分方程描述,对于单输入单输出的分数阶系统模型,可描述为:

其中,αi(i=1, 2,…,n)、βj(j=1, 2,…,m) —任意实数;
满足αn>αn-1>…>α0>0,βm>βm-1>…>β0>0,对上式进行拉普拉斯变换,可得到分数阶控制系统的传递函数为:
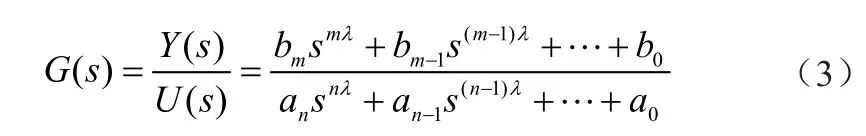
不同的控制系统和不同的控制器,可以将其分为以下几类:
(1)整数阶控制器控制的整数阶控制系统;
(2)整数阶控制器控制的分数阶系统;
(3)分数阶控制器控制的整数阶系统;
(4)分数阶控制器控制的分数阶系统[5]。
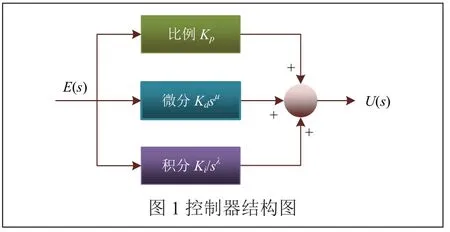
对于分数阶控制器,微分方程式为:
其中,Kp—比例系数;
Kd—微分系数;
Ki—积分系数;
μ—微分阶数;
λ—积分阶数。
经拉式变换得到对应时域传递函数表达式:
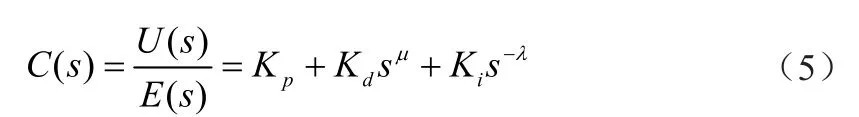
控制器对应的结构框图如图1所示。
三、卡尔曼滤波器和分数阶控制器实现
1、分数阶控制器实现
分数阶PIλDμ控制器设计是根据系统性能指标,得到满足系统要求的分数阶PIλDμ控制器优化Kp、Ki、Kd、λ、μ参数的过程。控制器参数的选择对控制系统起关键性作用,采用幅值裕量和相位裕度法对分数阶PIλDμ控制器进行参数整定。对于给定的相位裕度φm和截止频率ωc,根据参数整定规则,利用MatLab优化工具箱中fmincon非线性优化函数方法,可以求得分数阶 PIλDμ控制器Kp、Ki、Kd、λ、μ参数值[6]。控制器表达式为:
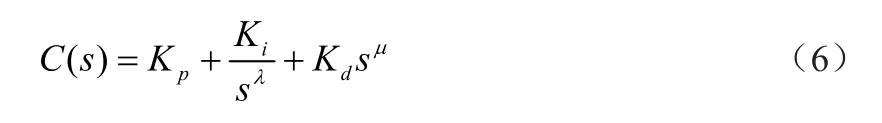
利用AL-Alaoui+CFE脉冲响应不变法对分数阶控制器进行离散化数字实现[7]。
2、卡尔曼滤波器实现
卡尔曼滤波理论以最小均方误差为估计的最佳准则,对于状态空间模型为:

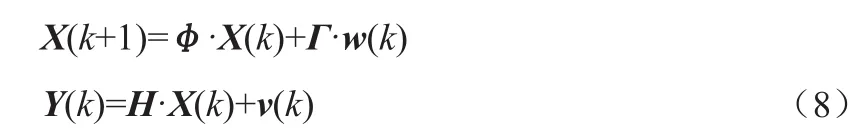
其中,A—状态矩阵;
B—输入矩阵;C—输出矩阵;
D—前馈矩阵,一般为零。离散化后状态空间模型为:
Γ—噪声驱动;
H—观测噪声;
k—离散时间;
X(k) —表示系统在k时刻的状态;
Y(k) —对应状态的观测信号;
w(k) —白噪声;
v(k) —观测噪声。
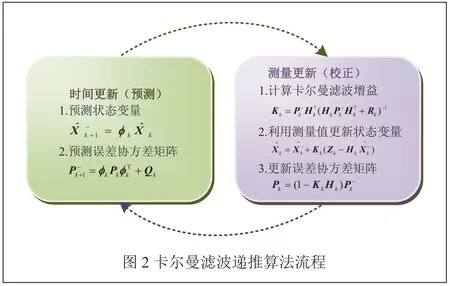

卡尔曼滤波的递推算法流程图如图2所示[8]。在一个滤波周期内,由预测状态变量可知,根据k时刻的状态估计预测k+1时刻状态,预测误差协方差是对预测的质量优劣做定量描述,该预测描述了卡尔曼滤波时间更新过程,测量更新中各式是用来计算对时间更新值的修正量,该值由等信息所确定,最终结果可以合理利用观测信号Y(k)。只要给定初值和P0,根据k时刻的量测Zk,就可以计算得到k时刻的状态估计
四、算法仿真分析
1、光电吊舱俯仰环模型建立
光电吊舱是包含线性和非线性因素的负载系统,难以通过物理建模法得到准确的系统模型,因此采用系统辨识的方法建立数学模型,通过实测输入输出数据对模型进行参数辨识。将某光电吊舱航向扫频信号作为系统输入,求得吊舱俯仰环在不同频率段的响应特性,最后通过系统辨识法求取系统的频率特性[9]。
通过可视化系统辨识工具箱对系统进行参数辨识[10],最后取部分实验数据对辨识模型进行验证,拟合得到俯仰环频率特性曲线如图3所示,不考虑延迟环节,近似得俯仰环的传递函数如下:
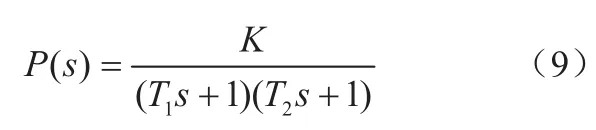
其中,K=1.449、T1=0.11、T2=0.0091。
2、仿真分析
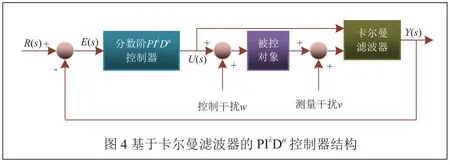
基于卡尔曼滤波器的分数阶PIλDμ控制器结构框图如图4所示。其中,被控对象采用零阶保持器进行离散化,分数阶控制器根据前文研究方法进行离散化实现,在系统运行和测量过程中产生的扰动经过滤波器滤除后的值Y(s)反馈到输入端与预定值进行比较后得E(s),作为控制器的输入值,U(s)为控制器的输出,w为控制干扰(过程噪声),v为测量噪声。
采用分数阶控制器与卡尔曼滤波器结合控制,假设系统开环截止频率ωc=90rad/s,相位裕度φm=60°,采样时间ts=0.001s,系统过程噪声和测量噪声均为协方差1,幅值0.02的白噪声,即Q=1,R=1,初始值P0=B*Q*B′。
由已知条件,根据参数整定规则,得分数阶控制器各参数为Kp=7.7212、Ki=35.6517、Kd=1.5847、λ=0.7404、μ=0.2558,传递函数表达式为:
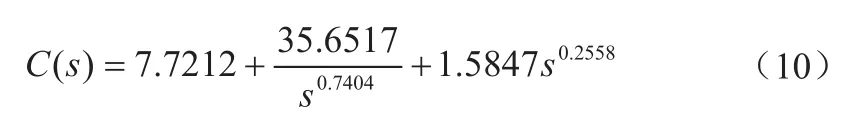
加入噪声前改变系统增益大小,Kp分别取原值的0.8倍、1.0倍、1.2倍,输入阶跃信号,仿真结果如图5所示。根据仿真结果可以得出系统动态响应特性,如表1所示。
根据结果分析可以得出,改变系统增益大小,系统动态响应特性变化较小,证明系统具有较强的增益鲁棒性,参数摄动不敏感,系统对控制输入信号具有良好的跟踪能力[11]。
加入滤波后,系统状态描述如下
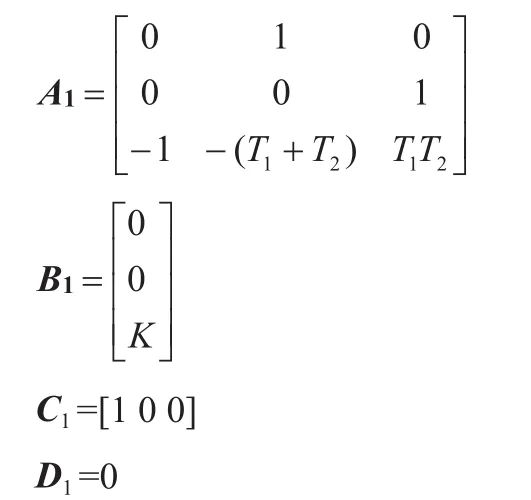
将连续时不变系统转换线性离散时不变系统:初始误差协方差P0为:

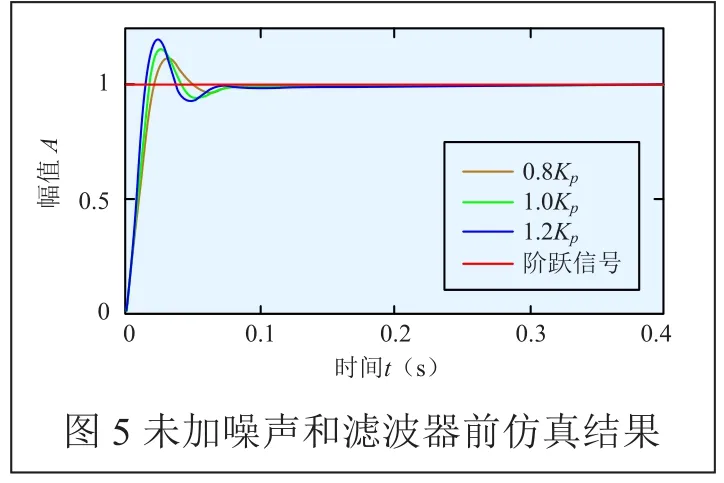
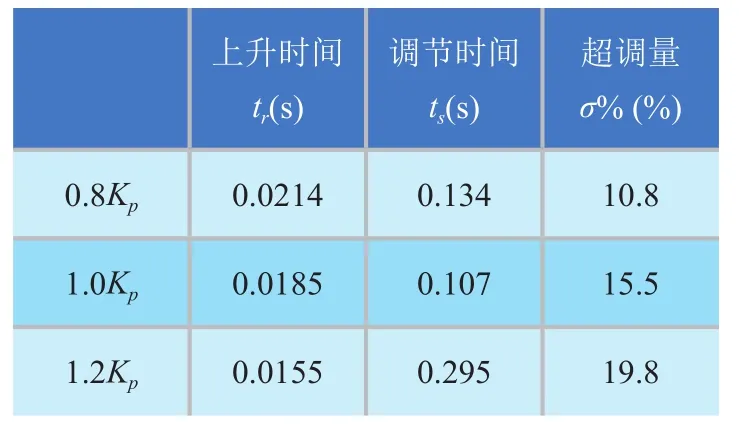
表1 系统动态响应特性

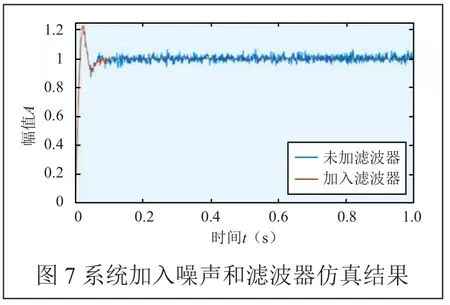
实验噪声大小情况如图6所示。加入滤波器后仿真结果如图7所示。由图7可以得出,系统在加入噪声和扰动后,未加入滤波器的动态响应特性,上升时间tr=0.0175s,系统加入干扰后,产生随机抖动,无法达到稳定状态,系统超调量σ%=22.5%;加入滤波器后的动态响应特性,上升时间tr=0.0175s调节时间ts=0.177s,系统超调量σ%=22.2%,系统在经过0.177s后达到稳定状态,响应速度较快。
实际系统中,噪声影响比实验中要复杂的多,卡尔曼滤波器在实际应用效果中有一定偏差,但整体满足到控制性能的要求。
五、结束语
本文主要以光电吊舱俯仰环为被控对象进行系统建模,通过改变系统增益大小,加入噪声干扰等条件,采用基于卡尔曼滤波器的分数阶PIλDμ控制方法与纯分数阶PIλDμ控制方法进行仿真对比研究,结果显示系统未加入噪声和滤波器前,纯分数阶PIλDμ控制器具有较强的增益鲁棒性,加入噪声和滤波器后,单纯的分数阶 PIλDμ控制器无法满足系统要求。基于卡尔曼滤波器的分数阶 PIλDμ控制器控制效果有明显改善,满足系统需求。