永磁直线同步电机矢量控制模型的优化与准确性分析

北京信息科技大学，北京 100192

一、引言

直线电机是一种把电能直接转化为直线运动机械能的电磁装置。其中，永磁直线同步电机（Permanent Magnet Linear Synchronous Motor, PMLSM）在位置精度、动态性能等方面都优于其它直线电机，目前开始应用于高精度数控机床的直驱进给系统，是一种性能优良的直线伺服电机[1]。由于PMLSM与负载之间实现了无机械零传动，没有了缓冲环节，当电机运行时，负载的变化，系统内部和外部环境产生的非线性扰动都直接传递至电机本身完全反馈作用于电机系统，使得系统对这些非线性扰动变得十分敏感，进而使系统的控制性能受到严重的影响。

针对电机在运行过程中出现的非线性扰动问题，除了电机本身结构的优化之外，目前主要在控制性能上进行优化，因此需要搭建出一个PMLSM的仿真模型，方便进行控制方法的分析与优化，一般在MatLab/Simulink仿真软件中进行直线电机的模型仿真搭建，但此软件并没有提供现有的直线电机模型[2-4]。

参考旋转电机的数学模型并结合直线电机的相关特性，首先建立了PMLSM的数学模型，构建出PMLSM伺服控制系统中三闭环控制结构，并基于电压空间矢量（Space Vector Pulse Width Modulation, SVPWM）的控制策略，详细给出了在Simulink环境下PMLSM仿真模型的搭建，最后通过对电机矢量控制的仿真实验，验证此模型的准确性。该模型为后续研究高精度的控制算法奠定了基础。

二、基于矢量控制的PMLSM数学模型

1、PMLSM矢量控制原理

矢量控制的实质是将励磁磁场与转矩解耦，就是通过空间坐标变换，使得交流电机的电枢磁场的方向与励磁磁场的方向在空间上保持正交，同时又能实现对电枢电流的幅值的控制，图1给出了电流的空间坐标系转换关系。

由图1可知各个坐标系可以互相变换，a-b-c坐标系通过Clarke变换矩阵变换到α-β坐标系公式为：

α-β坐标系通过Park变换矩阵变换到d-q坐标系公式为：

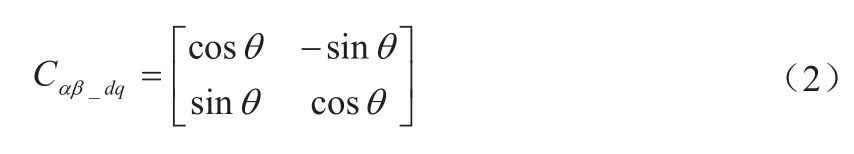
最终可以得出a-b-c坐标系到d-q坐标系的变换，同时得出ia、ib、ic与id、iq的变换关系：

在d-q坐标系下，电流可分为推力电流iq和励磁电流id，由上变换矩阵可知，只有实现对id、iq分别控制，就可以实现对ia、ib、ic的瞬时控制，则可完成电流的解耦控制，若分别对iq和id进行控制，只要能实现对三相电流ia、ib、ic的有效控制，就可以按照控制指令完成对交流电机的调速[5]。

2、PMLSM在d-q坐标系下的数学建模

一般为了简化分析可做如下假设[6]：

（1）磁路是线性的，忽略磁滞、涡流、剩磁和饱和等效应；

（2）绕组磁势及气隙磁密是按正弦分布的，并忽略空间谐波等。

在d-q坐标系下 PMLSM 的电压方程为：

磁链平衡方程：

其中，ud和uq—分别为d轴和q轴电压；

id和iq—分别为d轴和q轴的电流；

Ld和Lq—分别为d轴和q轴同步电感系数；

Ψd和Ψq—分别为d轴和q轴的电枢绕组磁链；

ΨPM—永磁体的有效磁通（在绕组中产生的磁链）；

Rs—直线电机的绕组电阻；

ω—动子电角速度，ω=NPωr；

NP—极对数；

ωr—机械角速度，ωr=πv/τ；

v—动子线速度；

τ—极距。

PMLSM的输入总功率为[7]：

由于研究对象的气隙均匀，则直轴的同步电感系数和交轴的同步电感系数相同，即：Ld=Lq。通过式（6）、 （7）、（8）可得出电磁推力表达式为： 根据牛顿第二定律得出运动方程为：

式中，m—动子质量；

FL—电机的负载阻力；

Fd—扰动力；

f—摩擦力。

三、PMLSM伺服控制系统仿真模型

1、PMLSM矢量控制伺服系统结构

PMLSM矢量控制伺服系统结构框图如图2所示[8]。 PMLSM伺服控制系统由电流闭环、速度闭环和位置闭环三环组成，采用空间矢量分析法，将定子电流进行和变换，获得在坐标系下的励磁反馈电流id*和推力反馈电流iq*，与给定励磁电流id和推力电流iq进行比较，通过q轴和d轴电流调节器产生给定励磁电压和转矩电压，再经过逆变换输出至α-β坐标系下的电压，最终决定SVPWM波形的输出[9]。图中解耦控制模块可消除永磁同步电机d-q轴电压ud和uq之间存在的旋转电动势对电流控制产生的影响，进而更准确的实现对id、iq的控制[11]。

2、PMLSM 仿真模型

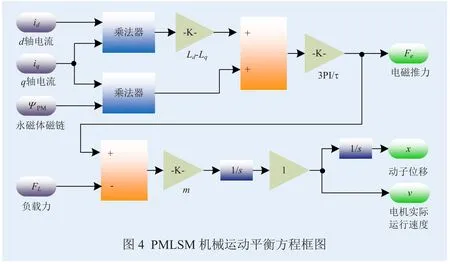
根据d-q坐标系下PMLSM数学模型，在Simulink仿真环境下搭建出PMLSM的仿真模型。由式（5）和式（6）可以建立电流仿真模块如图3所示，由式（9）和式（10）可以建立机械运动模块如图4所示。由此，将以上各个模块进行封装连接，得到PMLSM的Simulink整体仿真模型如图5所示[10]。

四、矢量控制的仿真实验

构建完毕后，再次对模型进行封装，可以将封装完毕的PMLSM仿真模型添加到Simulink工具箱中作为统一的模块使用。封装后的直线电机模型作为一个独立的模块，可以有效地连接其它电气模块来搭建PMLSM伺服系统[10]。根据图2 PMLSM矢量控制伺服系统结构框图，采用SVPWM控制方法搭建PMLSM整体伺服控制系统控制部分仿真模块如图6所示。

本文采用id=0的磁场定向空间矢量控制策略实现id、iq的解耦控制[13]。图6中，电流环采用的动子磁场定向控制方式，q轴和d轴反馈电流通过PID电流调节输出两轴控制电压。速度环根据速度误差大小，使用双闭环速PID速度调节，减小速度跟随偏差，最终通过SVPWM输出三相脉冲输送至逆变器部分。

本文中电机的参数为：三相电源电压为110V，动子质量m=8.4kg，动子电枢电阻Rs=1.9Ω，q轴电感Ld=11.6mH，摩擦系数Bv=0，永磁体有效磁链ΨPM=0.046Wb，极距τ= 0.021m，极对数Np=2。电机给定速度v*=0.1m/s，电机开始运行时加3N负载，0.5s开始变载为5N，运行此模型得出仿真实验结果。图7是直线电机三相电流、电磁推力和速度的仿真曲线[12]。

从图7速度仿真曲线结果中可以看出，电机在启动和负载突变这两个阶段，系统能很快达到给定的速度值，并且超调量很小，体现出很好的动态性能，从图中电磁推力、速度仿真曲线也可以看出，电磁推力和速度在达到给定值以后曲线很平滑，充分说明系统具有很好的稳态性能。

五、结论

本文阐述了矢量控制的基本思想，并基于d-q两相坐标系下的PMLSM数学模型，在MatLab/Simulink环境下搭建出PMLSM仿真模型，同时采用SVPWM矢量控制方式，构建出PMLSM整体矢量控制伺服仿真系统模型，通过对电机矢量控制的仿真实验结果的分析，充分说明了采用SVPWM矢量控制方式确实得到了很好的控制效果，并验证了该仿真模型的正确性, 为后续高精度控制器算法的研究奠定了基础。