基于灰色预测和SVM的茶叶烘焙温湿度预测

赵合胜

(湖南环境生物职业技术学院 医学院，湖南 衡阳 421005)

工业和农业的生产进程中，温度值和湿度量是关系着产品的生产质量的两个重要环境变量，人们经常必须要同时对温度和湿度进行控制.绿茶精细制作的关键的最后一道工序那就是恒温环境中的干燥，这一步的目的就是为了不让绿茶原有的色泽和香气流失，以利于保持清香型乌龙茶翠绿的色泽和高锐的清香[1-2].绿茶精制过程中有一道关键的工艺就是茶叶烘焙，这道工艺的效果对茶叶的保存时间、茶香及口感有很大的影响.目前，国内的绿茶烘焙手段主要使用的是炭焙和机焙两种方式，机焙是由人工使用木炭焙笼来烘制，操作过程由人工控制，操作工人的经验对烘焙效果影响比较大，茶叶质量难以得到稳定的控制；机焙采用电烘箱进行烘焙，使用较为广泛，国内外学者主要在温度和湿度控制方面进展飞速.文献[3]设计提出了一个用于控制温度量的模拟正交神经网络控制器，其主要应用于电热干燥方向；文献[4]针对于研究恒温箱内的温度环境变量控制的这一优化问题，设计的电加热器输出功率温度值的误差往往大于5 ℃的，湿度误差大于8%；文献[5]对夏季时节温室的温度和湿度控制用的是模糊神经网络，这一方式将遗传算法和模糊逻辑以及神经网络这3个算法进行了有机地结合后，将其应用于夏天温室的温度及湿度同步控制.针对绿茶烘焙过程,伴随着复杂的物质交换和热交换,温度及湿度不断变化并会伴随严重的耦合现象发生.文献[6]则就这个缺陷设计出了一种以逆模型解耦的变论域作为基础的模糊控制方式.该文方法能够有效提升绿茶烘焙过程的控制效果,提供了一种控制绿茶烘焙过程的新途径.

在烘焙过程中，温、湿度的控制非常重要，由于整个过程中的物理、化学环境的变化，会导致温、湿度相互影响，形成非线性耦合情况，所以建立绿茶烘焙加工阶段误差率极小的数学模型是有很大困难的，如果只是仅选用文献上面所述的控制方法以及各种策略是无法轻易地保证绿茶烘焙过程温湿度的精确控制，因此有必要进行绿茶烘焙过程工艺分析，建立烘焙过程温湿度预测模型，对于保证后续绿茶烘焙过程的稳定控制起到了关键性的作用.

灰色预测能对系统的将来行为进行超前控制，所以得出来的控制策略对该系统比较适应.它的结构简单，并且自适应性和实时性在它身上有较强的体现.对于复杂系统动态变化的过程它也是同样适用的[7].烘焙工艺物理、化学过程的复杂性，单一的预测模型难以较好地进行有效预测，而基于统计学习理论(Statistical Learning Theory,SLT)的支持向量机算法(Support Vector Machine,SVM)——一种新型机器学习方法却比较可行.绿茶烘焙是随机进行的，支持向量机(简称SVM)算法针对这样的一类具有非线性和小样本控制对象特性的过程也有着极优的学习能力，甚至于泛化能力[8].因此本文针对绿茶烘焙过程的复杂特性，提出一种基于灰色预测和SVM的绿茶烘焙过程温湿度预测模型，该模型首先利用灰色预测模型和SVM，分别对绿茶烘焙过程温湿度做预估，为了将两者进行有机融和，笔者选用熵值法确定各预测子模型的加权系数，进而得到了更为精准的绿茶烘焙过程温湿度预测模型结果，保证温湿度的稳定控制.

1 绿茶烘焙集成预测模型

茶叶烘焙过程由于电热丝和风机性能会呈现一点曲线变化，炉内热交换等物理、化学变化等因素影响，使得整个系统呈高度非线性状态，难以构造精确模型.一些学者利用基于专家规则的前馈补偿方法对绿茶烘焙过程进行解耦控制，其控制算法环境适应性较差.本文采用集成思想将灰色预测模型和SVM模型进行集成，建立绿茶烘焙的集成预测模型.

1.1 绿茶烘焙灰色预测模型

通过对绿茶烘焙温湿度的数据进行分析，可知绿茶烘焙温湿度的预估是带有灰色特性的，所以温度量和湿度量的预估问题是允许使用灰色预测来做预估的.本文以温度为例建立绿茶烘焙温度灰色预测模型.

假设系统中，温度的原始时间序列为：X(0)={X(0)(1),X(0)(2),…，X(0)(m)}，考虑到整个过程中的温、湿度会有瞬时性的峰值变动，所以直接用初始序列会产生比较大的误差值.笔者综合考虑新近时刻得到的数据与未来时刻的温度变量数值关联性比较大，为了能让本预测数据和实际的绿茶烘焙过程温度变化曲线相一致，故采用了加权平滑的方法来处理原始数列，使得其变化趋势更为均衡，让温度预测更加精准.我们采取加权生成算子来平滑处理茶叶烘焙温度的初始数据，如式(1)所示.

x′(k)=v1·x′(k)+v2·x′(k-1)+v3·x′(k-2)

(1)

(2)

最后，累减还原求解公式，得出温度量的预测模型.

1.2 绿茶烘焙SVM预测模型

由Vapnik等研究者提出来的SVM算法不但能够有效地进行非线性数据的处理，而且能限制过学习，另一方面又具有严格的理论及其数学的基础，剔除了局部极值，针对于网络的入侵检测这样的小样本学习上的应用具有很优的泛化能力，不过分依赖于样本的数量.标准SVM是一个凸二次优化的问题，它总是能够找到全局的最优解.然而当训练样本的数量增加的时候，因为有过于多的约束，从而大幅度增加了训练的时间以及内存需求，这个问题是SVM应用于实际的一大障碍.为了达到提高SVM的训练效率的目的，Suyken教授尝试改变一下标准SVM的约束条件以及风险函数，并由此提出了LS-SVM，即最小二乘支持向量机.LS-SVM的训练仅仅需要求解一个线性方程组，使得SVM易于实现，并极大程度上提高了SVM训练的效率.所以，笔者采用LS-SVM方法作为绿茶烘焙温湿度的预测方法.本文以温度为例建立绿茶烘焙温度SVM预测模型.

设绿茶烘焙温度预测训练样本集表示为(x1,x2,x3,x4,y)，其中，x1表示输入样本种类，x2为电热丝温度，x3为风机转速，x4为当前采样时刻绿茶烘焙温度，y表示输入样本对应的下一采样时刻的温度.进行线性回归，得到：

f(x)=[ω×φ(x)]+bφ:Rn→F,ω∈F

(3)

式(3)中，b是阈值.这一逼近问题等价于

(4)

式(4)中，‖ω‖2是平坦复杂性，C是惩罚因子，Rreg(f)是目标函数，s为样本数量，Remp(f)是风险函数,λ是调整常量.

(5)

对式(5)进行极小化处理，可以得到SVM回归函数，并采用拉格朗日乘子法以及核函数的方法来解决LM-SVM问题，从而进一步简化这个问题的线性方程组，然后求解，从而构建出绿茶烘焙温度集成预测模型.

1.3 绿茶烘焙集成预测模型

我们必须集成从时间角度出发建立的灰色预测模型和从空间角度建立的SVM温度预测模型，来达到使预测结果无限靠近茶叶烘焙温度量和湿度量的实际数值.笔者融合集成思想，采用熵值法确定最优加权系数，然后加权集成了灰色预测模型和SVM模型使其目标函数以预测偏差平方和最小，建立兼有两者预测输出的绿茶烘焙集成预测模型，来预测产生最终结果.图1是绿茶烘焙集成预测模型.

图1 绿茶烘焙预测模型的集成

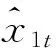
2 试验分析

试验样本选用产自江苏的碧螺春半成品，样本分为两份各10 kg，用于对比试验.采用目前绿茶烘焙过程中常用的PID算法以及上面试验推导出来的控制方法，对系统性能进行对比试验.其中，温度设定值为75℃，相对湿度设定值为30%.针对碧螺春生产工艺所采集的历史数据，建立灰色预测模型(GST)和SVM并分别预测绿茶烘焙温湿度数据，采用熵值法计算出绿茶烘焙集成预测模型中GST和SVM的加权系数.文中选择样本点为50个.选用绝对值平均相对偏差MAPE和均方根相对偏差MSE用以评价三种不同模型的预测效果和各自的性能(见表1).与灰色预测模型相比较来说集成预测模型的预测性能得到了许多改善：它的MSE由最初的0.010减少到了0.006，而MAPE则由0.015减少到了0.012.这两个评价指标值的降低，足以证明集成预测模型比灰色预测模型预测精度高并且性能好.而与SVM神经网络模型相比较的话，集成预测模型的MSE则由0.013降低到0.006，MAPE由0.020降低到0.012，这些数据也能够证明集成预测模型比SVM模型预测精度高且性能好.即集成预测模型明显优于两种预测模型.

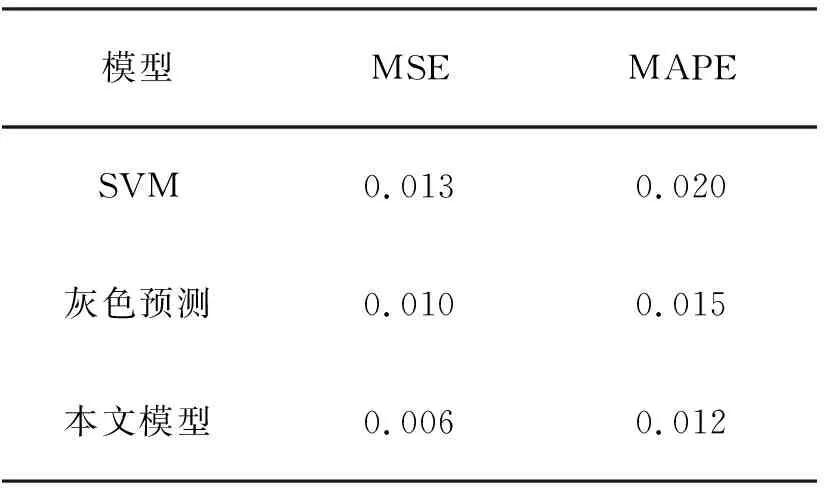
表1 三种模型性能与误差对照表

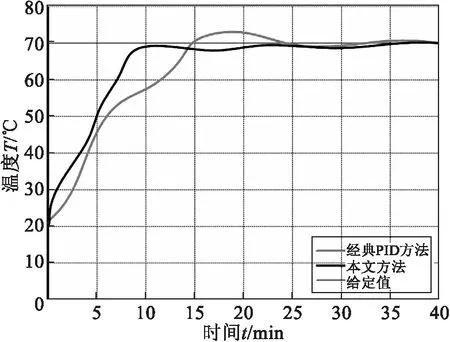
图2 温度对比试验曲线

采用本文提出的预测方法+PID控制后，图2分别为在烘焙过程中温度变化试验对比曲线.由于采用了预测模型，控制精度相对于传统的PID方法有了较大的提高，较好的保证了温湿度的精确控制，提升了绿茶香气和品质.

3 结论

本文在对绿茶烘焙过程深入分析的基础上，针对绿茶烘焙过程中，物理化学复杂，温、湿度之间具有很强的耦合度，提出了一种基于模糊系统解耦茶叶烘焙温湿度控制方法.首先采用单独PID控制器分布对温湿度进行控制，然后采用模糊解耦控制方法，实现温、湿度补偿解耦，应用效果表明了该方法的有效性.