题海无边 “回头”是岸—2018年高考全国II卷理科数学导数压轴题分析与备考建议

广东省广州市第四中学(510170) 左巍波 刘运科

目前,高考经常以函数导数题作为压轴题.导数压轴题在考查基础知识的基础上,注重对能力的考查,注重对数学思想方法的考查,具有综合性强,思维量大,方法繁多,技巧性强等特点.本文对2018年高考全国II卷理科数学第21题进行了分析,并给出了导数压轴题的备考建议,希望能高考的教学备考起到抛砖引玉的作用.

一.试题分析

高考真题(2018年高考全国II卷理科第21题)已知函数f(x)=ex-ax2.

(1)若a=1,证明：当x≥0时,f(x)≥1;

(2)若f(x)在(0,+∞)只有一个零点,求a.

第(1)问证法1当a=1时,f(x)≥1等价于(x2+1)e-x-1≤0.设函数g(x)=(x2+1)e-x-1,则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x.当x/=1时,g′(x)＜0,所以g(x)在(0,+∞)单调递减(如图1).而g(0)=0,故当x≥0时,g(x)≤0,即f(x)≥1.

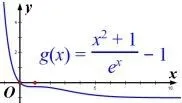
图1

图2

第(1)问证法2当a=1时,f(x)≥1等价于ex-x2-1 ≥ 0.设函数g(x)=ex-x2-1,则g′(x)=ex-2x,g′′(x)=ex-2.

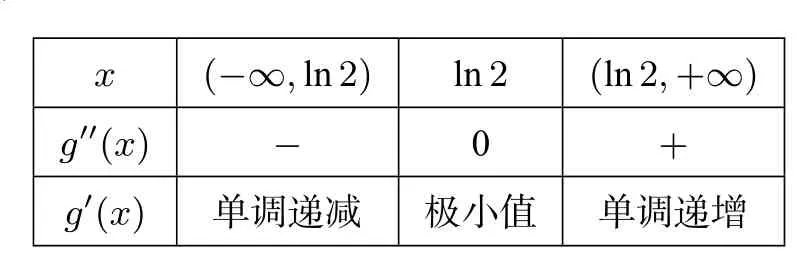
x (-∞,ln2)ln2(ln2,+∞)g′′(x)-0+g′(x)单调递减极小值单调递增

所以,g′(x) ≥g′(ln2)=eln2-2ln2=2-2ln2＞0,g(x)在上单调递增(如图2),故当x≥0时,g(x)≥g(0)=e0-02-1=0,即f(x)≥ 1.

点评利用导数证明不等式的常见方法是：构造函数g(x).一般有两个步骤.第一步是构造,把待证明的不等式等价变形为g(x)≥0(或g(x)≤0);第二步是证明,利用导数求g(x)的单调性,证明g(x)min≥0(或g(x)max≤ 0).待证明的不等式有多种等价变形形式,导致证明方法有多种.

证法2是构造直接作差函数g(x),证法1是作差之后再同除以ex构造函数g(x),两种方法各有优劣.从构造的过程来看,证法1的构造过程比较复杂,证法2直接作差,构造方法更加自然;从构造之后的证明过程来看,证法1涉及到除法求导公式、判断导数值恒非正,而证法2需要求二阶导、判断导数值恒为正,证法2的难度比证法1稍大.

第(2)问解法1设函数h(x)=1-ax2e-x.f(x)在(0,+∞)只有一个零点当且仅当h(x)在(0,+∞)只有一个零点.

(i)当a≤0时,h(x)＞0,h(x)没有零点;

(ii)当a＞0时,h′(x)=ax(x-2)e-x.当x∈(0,2)时,h′(x)＜0;当x∈(2,+∞)时,h′(x)＞0.所以h(x)在(0,2)单调递减,在(2,+∞)单调递增.故是h(x)在(0,+∞)的最小值.

①若h(2)＞0,即,h(x)在(0,+∞)没有零点;

②若h(2)=0,即,h(x)在(0,+∞)只有一个零点;

③若h(2)＜0,即,由于h(0)=1,所以h(x)在(0,2)有一个零点,由(1)知,当x＞0时,ex＞x2,所以.故h(x)在(2,4a)有一个零点,因此h(x)在(0,+∞)有两个零点.综上,f(x)在(0,+∞)只有一个零点时,(如图3).

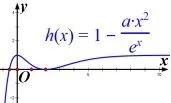
图3

图4

图5

第(2)问解法1(别解)

①②同解法1.③若h(2)＜0,即,由于h(0)=1,所以h(x)在(0,2)有一个零点,由洛必达法则可知[1],当x→+∞时,h(x)=1-ax2e-x→1,所以h(x)＞0.故h(x)在(2,+∞)有一个零点,因此h(x)在(0,+∞)有两个零点,不合题意.(余下同解法1)

第(2)问解法2f(x)在(0,+∞)只有一个零点当且仅当f(x)=0在(0,+∞)只有一个解,即只有一个解,即直线y=a与曲线在(0,+∞)只有一个交点.,

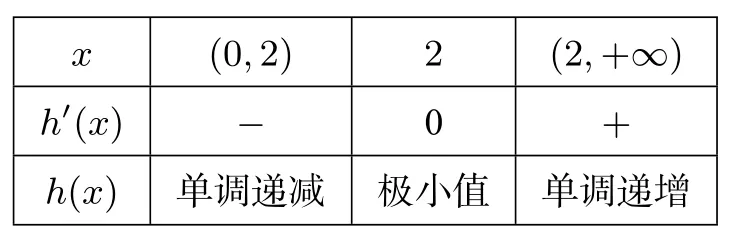
x (0,2)2(2,+∞)h′(x)-0+h(x)单调递减极小值单调递增

第(2)问解法3f(x)在(0,+∞)只有一个零点当且仅当f(x)=0在(0,+∞)只有一个解,即只有一个解,即直线y=ax与曲线在(0,+∞)只有一个交点.,

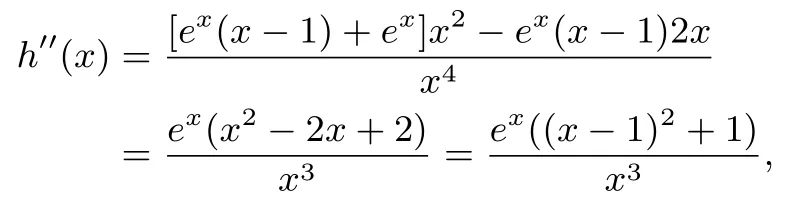
x＞0时,h′′(x)＞0恒成立,在 (0,+∞)上是凸函数.考虑过原点O(0,0)的直线y=ax与曲线相切于点.切线斜率k=,另一方面,切线斜率由得.从而,在(0,+∞)只有一个零点时,(如图5).

点评函数的零点问题,一般有两种转化思路：一种是从代数角度,转化为解方程问题;一种是数形结合,转化为函数与x轴的交点(或两个函数的交点)问题.本题采用数形结合的转化思路.本题的条件有多种等价转化形式,导致解题方法有多种.

解法2将其转化为直线y=a与曲线在(0,+∞)只有一个交点,用“分离变量”的方法求解.分离变量法是处理含参函数问题的一种常见的方法.用分离变量法的难点在于：要说明在x→0+、x→+∞时的极限;h(x)在x→0+时的极限容易说明,在x→+∞时的极限需要用到洛必达法则.

解法3将其转化为直线y=ax与曲线在(0,+∞)只有一个交点,用“切线法”求解.切线法也是处理含参函数问题的一种常见的方法[2].切线法的解题原理是凸函数的几何性质：凸函数的图像在任一点的切线的上方.用切线法的难点在于：需要额外学习凸函数的相关知识.

二.备考建议

《2018年高考理科数学考试大纲》指出,数学的命题“在考查基础知识的基础上,注重对数学思想方法的考查,注重对数学能力的考查”,“同时兼顾试题的基础性、综合性”[3].本题很好地体现了考试大纲的要求,主要考查的知识点有：函数的单调性、函数的极值与最值、不等式恒成立问题、函数的零点问题等.本题考查了推理论证能力、抽象概括能力、运算求解能力,涉及到的数学思想方法有：转化与化归思想、函数与方程思想、分类讨论思想、数形结合思想.

每年的高考评卷结果显示,导数压轴题的平均分极低,大多数考生基础得分得不到保障,很多考生得0分;能拿到6分以上的考生少之又少,得满分的考生更是凤毛麟角.而在实际的备考中,大多数考生花费了大量时间来进行训练,为什么连基础的得分都得不到保障呢?导数压轴题的平均分低,一方面是因为考试时间紧张,考生缺乏足够的时间来做压轴题;另一方面也反映出导数的复习备考有待进一步优化.如何优化函数导数的备考呢?关键是要跳出题海,科学备考,题海无边,“回头”是岸.下面提出4点备考建议,供大家参考.

1.研究高考试题,结合考生实情,明确备考方向

要重视对高考真题的研究,结合考生的实际能力水平,确定备考的目标和方向.要研究近几年高考真题,分析试题的异同,寻找一般规律,明确考试的内容.要分析考生的实际能力水平,确定目标,明确方向,既不能好高骛远、眼高手低,也不要固步自封、裹足不前.

2.重视基础知识,落实基本方法,确保基础得分

要重视函数导数的基础知识、基本方法,通过基础训练,来落实基础知识、基本方法.不要急于求成,一开始暂时不训练较难的方法,而是专注于训练基础知识、基本方法.可以把模拟题、历年高考真题第一问挑选出来,按基础知识点或基本方法进行分类,再编排成基础训练小专题,专门训练函数导数的第一问.根据对历年高考题的研究,要重视下列几个基础知识、基本方法的训练：

(1)求导：两个函数相乘、相除的求导,复合函数求导.

(2)求切线：设切点坐标求切线,已知切线求参数的值.

(3)简单函数的图像与性质：f′(x)=0有解的函数的单调性、极值最值、零点.

3.重视通用方法,适当补充拓展,提升学生能力

当基础知识、基本方法训练落实到一定程度之后,可以进行通用方法的专练.同样地,一开始不训练压轴题,而是要训练常规题、中档题,专注于通用方法的训练.高考压轴题难度太大,可将其改编成简单题、基础题,进行训练;部分较难的导数压轴选择题、填空题,也可以改编成解答题,进行训练.根据对历年高考题的研究,要重视下列几个热门考点、通用方法的训练：

(1)证明不等式：直接作差构造函数,证明不等式.

(2)简单的分离变量法：分离变量,数形结合,求参数的值或取值范围.

(3)简单的分类讨论：进行简单的分类讨论,求含参函数的单调性.

图6

图7

图8

当通用方法训练落实到一定程度之后,可以结合考生情况,适当补充拓展,进行拓展方法的专练.此阶段可以直接进行历年高考真题、高考模拟题的训练.根据历年高考情况,建议以专题的形式,补充下列几个热门考点、拓展方法的训练：

(1)证明不等式：变形构造函数,证明不等式.

(2)分类讨论：复杂的分类讨论的策略.

(3)恒成立问题：处理恒成立问题的策略.

(4)零点问题：零点问题的转化求解策略.

(5)极限与洛必达法则：结合单调性、极限、洛必达法则,得到不熟悉函数的图像.

(6)凸函数与切线法：凸函数的定义与性质,用切线法解决不等式问题.

(7)隐零点问题：虚设零点,设而不求的策略.

(9)极值点偏移问题：极值点偏移问题构造函数的策略.

(10)双变量问题：双变量问题的构造整体策略、主元法策略等.

4.重视反思总结,渗透数学思想,提升数学素养

2018年1月16日,教育部颁布了《普通高中数学课程标准(2017年版)》,提出了六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[4].《课标(2017年版)》将于2018年秋季开始执行,2018年至2020年这三年的高考,是处于过渡阶段的高考.2018年仍然按旧的标准和考纲进行命题,命题人也在积极探索以素养为导向的命题工作,重视考生数学素养的形成和发展,正在实现从能力立意到素养导向的历史性转变[5].

本题主要考查了学生的3个方面的核心素养：数学抽象、逻辑推理、直观想象.要解决此题,学生需要理解相关概念(导数、极值、最值、零点),理解待证明的命题的条件与结论,理解方法规则(分离变量法)—这就是数学抽象.学生需要能够理解和构建知识之间的联系(转化与化归);能够用数学语言表达规则、推理和论证—这就是逻辑推理.学生需要能够借助图形性质探索解决问题的思路(数形结合),体会几何直观的作用和意义—这就是直观想象.

核心素养的培养和提升不是一句空话,要在教学中落实.对于解题的教学,要重视解题反思,要重视方法的总结,渗透数学思想方法,提升数学核心素养.反思总结应该有三个层次：回顾解题、方法提炼、思想渗透.例如,对于本题,反思总结可以按如下的思路进行：

(1)回顾解题.包括重新分析题目条件、目标,回顾解题过程,指出注意事项;

(2)方法提炼.指出问题的本质,提炼一般方法;对比多种方法,分析各种方法的优劣;思考结论的逆命题、否命题是否成立,思考结论或方法能否推广.

(3)思想渗透.指出问题涉及到的数学思想.导数问题特别要重视三个数学思想：转化与化归思想、函数与方程思想、数形结合思想.例如,近几年全国卷理科数学导数压轴题,很多都要用到数形结合思想：

数形结合思想在导数压轴题中的应用

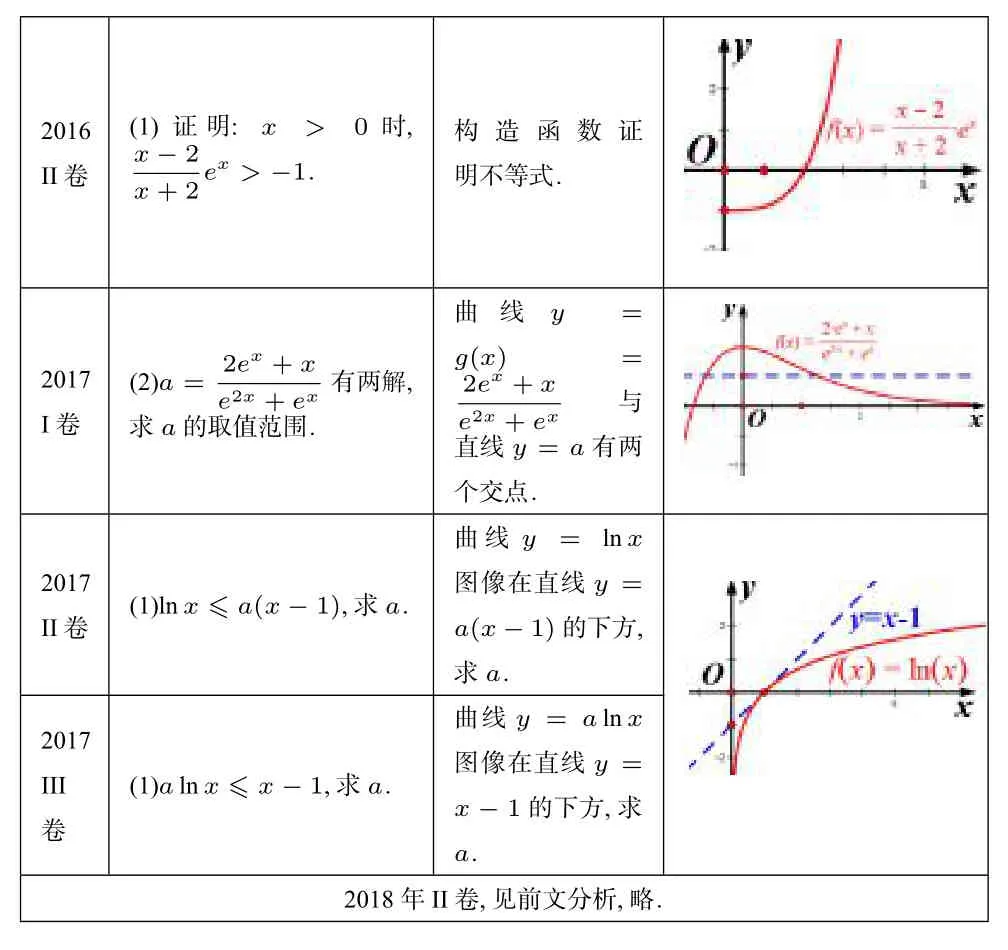
2016 II卷(1)证明：x＞0时,x-2x+2ex＞-1．构造函数证明不等式．2017 I卷(2)a=2ex+xe2x+ex有两解,求a的取值范围．曲线y=g(x) =2ex+xe2x+ex与直线y=a有两个交点．2017 II卷(1)lnx ≤a(x-1),求a．曲线y=lnx图像在直线y=a(x-1)的下方,求a．2017 III卷(1)alnx ≤x-1,求a．曲线y=alnx图像在直线y=x-1的下方,求a．2018年II卷,见前文分析,略．

波利亚把解题分为四个阶段：“弄清问题、拟定计划、实现计划、回顾.”[6]题海无边,“回头”是岸.回头、回顾,就是解题之后的反思总结.重视解题反思,渗透数学思想,可以更好地培养学生思维品质,提高学生的分析问题、解决问题的能力,提升学生的数学素养.