大学生综合成绩的模糊综合评价方法

2018-11-15郭竹梅

重庆科技学院学报（自然科学版） 2018年5期

郭竹梅

(安徽科技学院信息与网络工程学院，安徽凤阳 233100)

学习成绩评定对大学生而言至关重要，关系到他们的学习态度和切身利益，因此要力求评定结果的合理与公正。学生的综合成绩由多门课程成绩合成，只有将他们的各门课程成绩进行综合评价，合理地定量化，才能得出客观、科学的结论。

模糊综合评价法是根据模糊数学的隶属度理论把定性评价转化为定量评价，用模糊数学对受到多种因素影响的对象进行综合评价。在学生学习成绩评价方面，已经有许多人尝试运用模糊综合评价法。比如：用模糊综合评价法评定学生的课程平时成绩[1]，用模糊综合评价法评定学生的毕业实习成绩[2]等。学生的综合成绩涉及多门课程的成绩，也是一种受到多种因素制约的评价对象。运用模糊综合评价法来评价学生的综合成绩，其结果应该是更合理、更客观的。为此，我们尝试运用模糊综合评价法来评价学生的综合成绩。

1 评价模型的建立

对学生的综合成绩进行模糊综合评价，首先需要建立模糊综合评价模型。

第一，确定因素集。

学生的综合成绩涉及多门课程的学习成绩。要评价某个学生在某个学期的综合成绩，则评价因素就包括该学生在这个学期所学全部课程的成绩。

尝试对信息与计算科学专业某班学生在2017 — 2018学年第1学期的综合成绩进行模糊综合评价。该班在这个学期开设的主要课程有10门，则以这10门课程的成绩作为因素集。

U={u1,u2,u3,u4,u5,u6,u7,u8,u9,u10}

其中，u1～u10分别为课程数学分析I、高等代数I、解析几何、专业导论、形式与政策I、大学计算机基础、中国近现代史纲要、大学英语I、大学体育I、安全教育的成绩。

第二，确定评语集。

将学生的综合成绩分为5个等级：(Ⅰ)优秀、(Ⅱ)良好、(Ⅲ)中等、(Ⅳ)合格、(Ⅴ)不合格。各等级的成绩分数范围：优秀90～100分，良好80～89分，中等70～79分，合格60～69分，不合格0～59分。

V={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}

第三，确定各因素的权重。

根据学校对该专业各门课程赋予的学分，确定各因素对应的权重(见表1)。

表1 各因素对应的权重

第四，建立模糊矩阵。

利用下列隶属函数，得到模糊矩阵(R)，最后进行模糊综合评价。

B=A°R

2 实例分析

信息与计算科学专业某班2017 — 2018学年第1学期学生的课程成绩如表2所示。

选取1号学生的成绩为例。把他的10门课程的成绩代入隶属函数中，可得如下模糊矩阵。

由此计算评定1号学生的综合成绩。

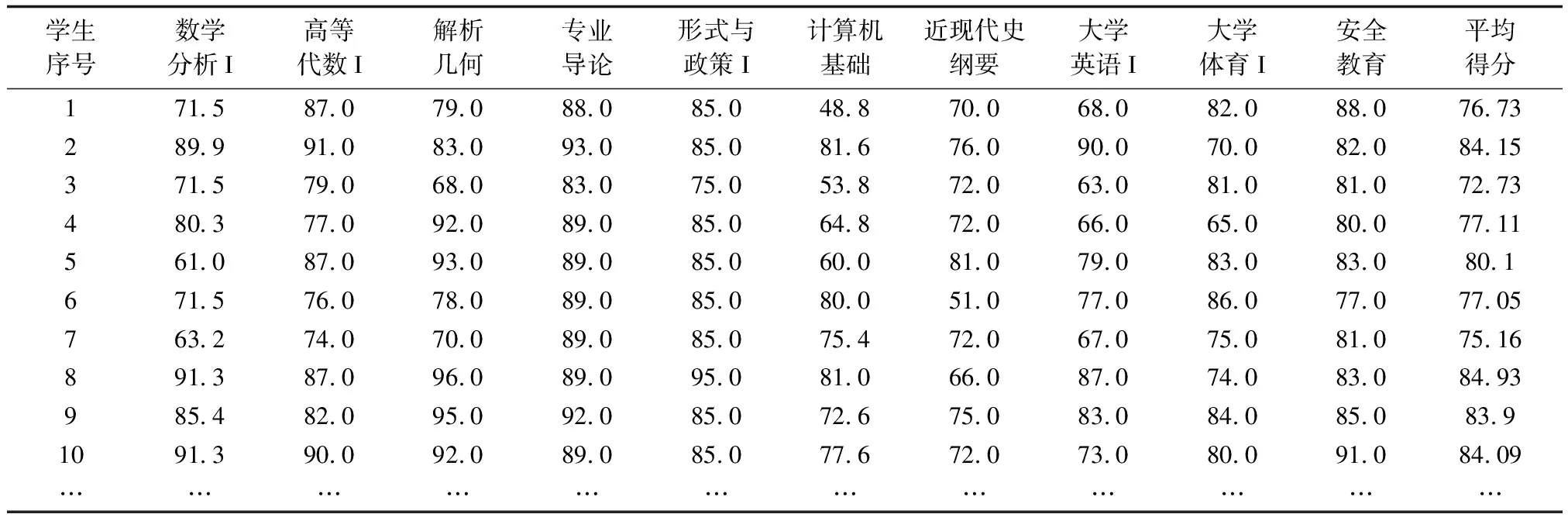
表2 学生的课程成绩统计

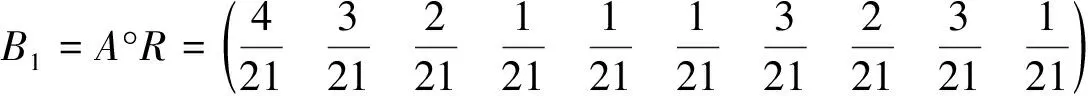
根据最大隶属度原则，1号学生的综合成绩可评定为“良好”。

再以7号学生为例。把7号学生的10门课程成绩代入隶属函数中，得到如下模糊矩阵。

由此计算评定7号学生的综合成绩。

根据最大隶属度原则，7号学生的综合成绩可评定为“中等”。

从表2可以看出，1号学生和7号学生的课程平均得分的差距很小，分别为76.73分、75.16分。如果仅以课程平均得分来评定学生的综合成绩，则1号和7号学生在这学期的综合成绩均为“中等”。用模糊综合评价法来计算评定，这两个学生的综合成绩则出现了等级上的差异，一个为“中等”，而另一个为“良好”。模糊综合评价法全面兼顾了各因素的权重，得出的结果是比较客观的。