动车组故障数据的统计分析及其应用
2018-11-15王灵芝
王灵芝
(中国铁道科学研究院集团有限公司 机车车辆研究所,北京 100081)
目前,中国高速动车组的信息采集技术不断增强,最新的复兴号动车组已经能够采集多达1500项动车组的状态信息。其覆盖了动车组很多设备,也包括了动车组设备所处的环境温度、设备的磨损情况等。设备出现异常时系统可自动报警,并将设备出现的异常情况采集记录下来。这些信息通过远程传输使得地面及时获知设备的当前状态。
信息采集技术能够将动车组整个生命周期内的运行状态、故障信息以及维修情况及时完整地记录下来。这些信息为动车组故障的诊断提供依据,通过对故障信息的统计分析,为动车组修程修制的优化、售后备件种类和数量的优化、动车组设备的正常运行提供帮助。
通过对故障信息的宏观统计分析,工作人员不仅可以获取故障多发的时间、多发的线路、多发的设备,还可以获取主要的故障模式、故障原因、故障影响因素等。对故障信息的深度统计分析,可以优化设备的维修间隔期、调整各级别修程的维修内容、合理调配维修资源[1]。
1 动车组设备分级树的建立
动车组属于大型设备,其结构复杂、部件种类繁多,因此设备发生故障的概率很大。为了更加科学地对动车组设备进行故障信息的统计分析,对动车组的层次化、模块化特点建立设备分级树。对故障信息进行分析时,按照设备分级树的层级对故障信息进行筛选,使故障信息的统计分析更加条理清晰[2]。
动车组设备分级树的部分结构如图1所示。整个动车组划分为车内系统、牵引传动系统、制动系统、转向架、高压系统、网络控制系统、辅助供电系统。第二层级是制动系统,分为风源分系统、防滑分系统、制动控制分系统、基础制动分系统等。第三层级是制动控制分系统,分为风缸、制动控制装置等。第四层级是制动控制装置,分为停放控制模块、供风模块、制动控制模块、电子制动控制单元等。第五层级是制动控制模块,分为电磁阀、空重阀和压力变换阀等。采用类似方法对动车组所有系统、分系统进行设备分级树的构建,最后形成完整的动车组设备分级树。
根据不同的需求,对不同层级的不同产品进行故障统计分析。例如,动车关注的是系统、分系统层级的故障,动车段关注的是装置、部件层面的故障,主机厂和配件厂关注的是装置、部件、零部件的故障。它们可以按照自己的需求,对信息系统的故障按设备分级树的方法进行筛选分析,得到准确的结果。
2 故障信息的宏观统计分析
信息系统中每条故障信息至少包含了故障时间、故障部件、故障名称、故障系统、故障现象、故障原因、故障影响以及故障解决方案等。依据上述设备包含的信息选择分析层级,无论选定哪一层级作为分析对象,统一将分析对象称为设备。某动车组各系统故障数据统计分析,如图2所示。
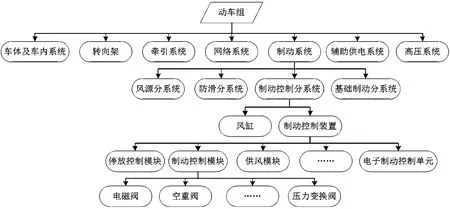
图1 动车组设备分级树的部分结构
从各系统故障发生的频次来看,车体及车内系统、牵引系统和高压系统故障频次较高。车体及车内系统与乘客和乘务人员频繁接触、使用率高,其故障主要集中在车门和卫生供水系统。因此,多准备相关的配件,及时对故障件进行更换或修复。高压系统中的受电弓部分暴露在动车组车顶,受外部环境影响很大。受电弓一旦发生故障,排查维修作业用时较长,耽误行车时间较多。针对这种情况,工作人员必须保证受电弓动态监测系统的有效、可靠,及时发现受电弓状态的异常避免故障的发生。牵引系统结构复杂,任何零部件的不良都有可能影响牵引功能的运作。传感器故障、板卡故障是导致牵引功能出现异常的主要原因,其无法通过实时监测提前预知,因此这些零部件在设计生产阶段需保证较高的质量。
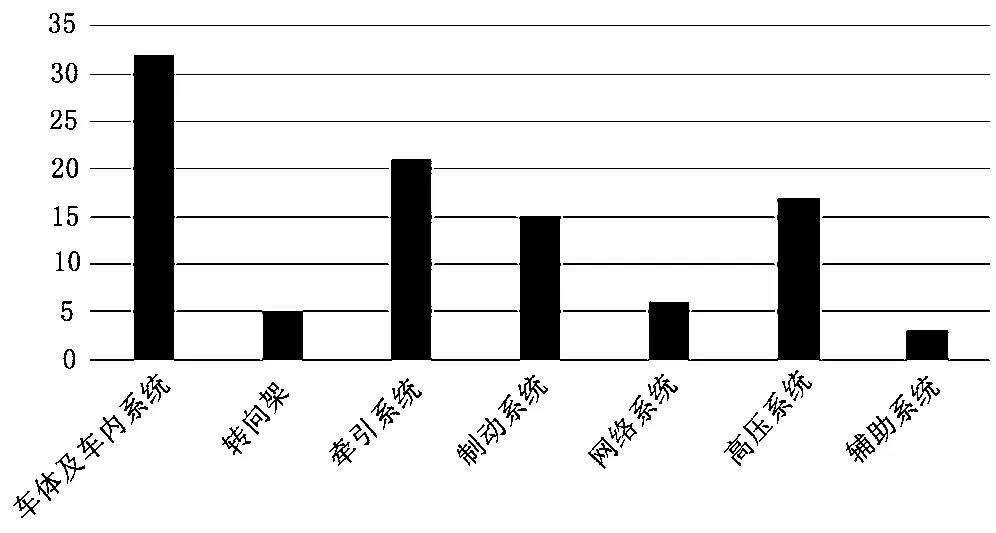
图2 动车组各系统故障数据统计分析
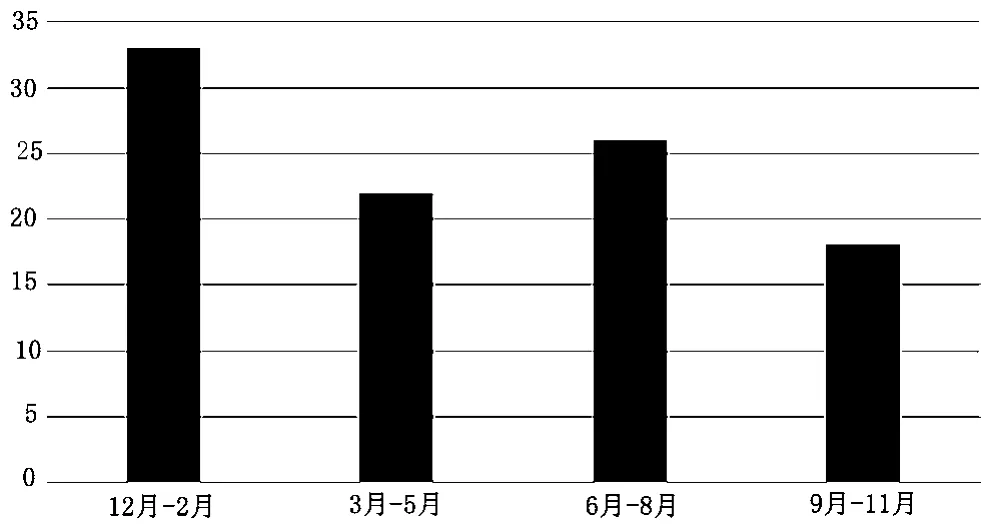
图3 动车组全年各季度故障数据统计
不同季度统计的故障数据如图3所示。12~2月故障最多,冬季天气恶劣,极端暴风雪天气对制动系统和车体及车内系统都是严峻的考验。车门处积冰等情况对车门控制系统影响很大,气温过低对橡胶件的密封性能也会产生一定影响。因此,在冬季特别是运行线路在北方的动车组需准备充分的备品备件。
3 故障信息的深入统计分析
3.1 故障率函数的确定方法
故障率是指设备工作到t时刻后,在单位时间内的故障发生概率,它反映了研究对象在任一瞬时出现故障概率的变化趋势[3]。
故障率如式(1)所示。
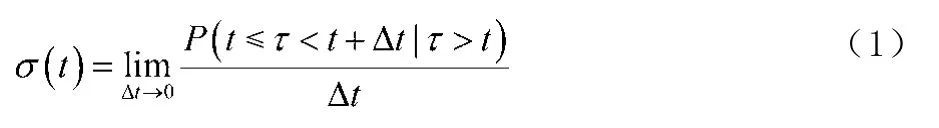
将设备的故障率σ(t)随时间变化的函数用曲线在坐标σ(t)-t上绘出,它反映了设备工作全过程的故障变化情况。
对于动车组某层级的一种设备,假设在运行时刻t=0时K个设备开始运行,到时刻t时有Kf(t)个设备发生了故障,这时还有K-Kf(t)个设备继续运行,继续运行Δt时间后,又有ΔKf(t)个设备发生故障,则工作到t时刻的设备在单位时间内的故障率表达式如(2)所示。

根据故障信息便可以得到所分析设备离散时间点的故障率,将这些离散时间点故障率用曲线坐标σ(t)-t绘出,进而通过对离散时间点的故障率进行曲线拟合,得到设备的故障率分布函数。
动车组设备修程修制的设备预防性维修间隔期自始至终都是相同的,这是基于所有预防性维修活动能够在设备在维修后,保持如新品一样高的可靠度。实际情况是,预防性维修很难使设备达到修复如新的程度,设备已经运行的时间、预防性维修话费的费用等都会对预防性维修后的效果产生影响。如果设备的故障率随着工作时间的增长而逐渐增加,那么随着维修次数以及设备运行时间的增加,设备的可靠性会逐渐降低。根据上述故障率分布函数的获取方法同样可以得到设备第一次维修、第二次维修、第三次维修等,每次维修后的故障率分布函数σ1(t)、σ2(t)、σ3(t)等。
3.2 故障率函数在维修决策中的应用
动车组设备众多,功能千差万别,每个设备的要求也不尽相同。因此,在制定维修计划时,每种设备的侧重点也不同,但总的来说不外乎以下几个方面。设备维修费用率最小,设备达到最大的可用度,设备在满足可靠度要求的前提下要求维修费用率最小[4]。
3.2.1 维修费用率最小计算模型
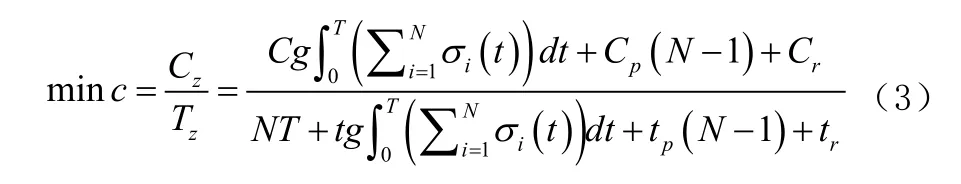
式中,Cg表示设备发生故障进行一次修复所需费用;Cp表示设备运行到维修时间点进行一次预防性维修所需费用;Cr表示更换设备所需费用;T表示设备两次预防性维修之间的运行时间;N表示设备被更换前经历的预防性维修次数;tg表示设备发生故障进行一次修复所需时间;tp表示设备进行一次预防性维修所需时间;tr表示设备进行一次更换所需时间。此模型中的决策变量为T和N,其他参数都可以通过信息系统记录的相关信息得到。
3.2.2 可用度最大计算模型

式中,NT表示设备正常运行的时间,分母部分表示设备正常运行时间以及各种维修所需时间之和。此模型中的决策变量为T和N,其他参数都可以通过信息系统记录的相关信息得到。
3.2.3 在满足可靠度要求的前提下维修费用率最小计算模型
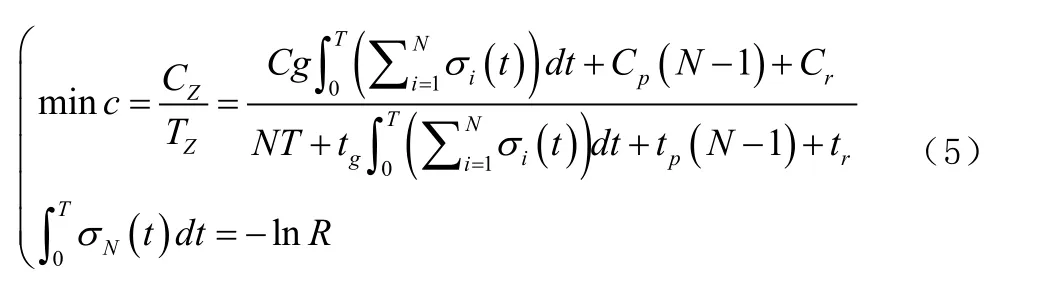
式中,N表示设备必须满足的可靠度,一旦低于此可靠度则必须对设备进行维修。此模型中的决策变量为T和N,其他参数都可以通过信息系统记录的相关信息得到。
3.2.4 成组维修模型
分析了单个设备的预防性维修间隔期优化模型,对于动车组这样一个庞大的系统来说,仅按单件所确定的最优维修决策并非最优。因此,不可能依照这些维修间隔期来执行,否则系统就需要不断地停机来进行维修,而应将任务集中起来形成成组维修策略[5]。
假设某一系统,包含M种子件,n为在设定时间短(0,tend)时间内对系统进行维修的次数。Cpk表示部件p在系统完成k-1次维修后到第k次维修所产生的维修费用。SK表示系统因维修停止运行所产生的损失费用。Tparkk系统第k次预防性维修所产生的停运时间表达式如式(6)所示。
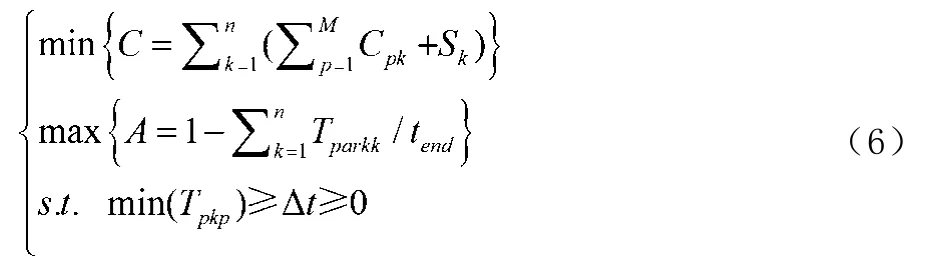
4 结语
本文描述了动车组设备分级树的建立方法,依据分级树的层级对故障信息进行筛选分析,并介绍了故障信息的宏观分析方和深层分析方法,给出了设备故障率函数的获取方法。在此基础上,本文研究了单设备的维修间隔期优化模型,并给出了多设备综合维修的优化模型。
