箱型钢管混凝土构件在纯扭作用下的数值分析

吴成龙, 刘继明, 赵凯常, 胡贻斌, 张保涛

(青岛理工大学 土木工程学院, 山东 青岛 266000)

自20世纪80年代以来,我国的基础设施建设发展迅速,钢管混凝土这一新兴组合结构得到广泛应用,主要原因在于混凝土中配置的钢管克服了钢筋混凝土结构的诸多弱点,其结构性能得到改善,使其具有钢管和混凝土两者的性能优势.因此,钢管混凝土结构在强度、刚度及稳定性能等方面比钢结构和钢筋混凝土结构表现出了更优异的性能[1-6].目前,国内外对型钢混凝土结构的主要研究焦点集中在地震作用下,构件的受弯性能及梁柱节点的抗震响应问题.对于钢管混凝土结构承受扭矩作用下受力性能的研究尚不深入,因此,研究扭矩作用下箱型钢管混凝土构件的受力性能具有重要的现实意义.

笔者拟对设计的13个模型试件进行有限元分析,由此来探讨纯扭作用下,试件中各组成部分的应力情况,分析钢筋混凝土构件、外包填充式箱型钢管混凝土构件以及填充式、外包式箱型钢管混凝土构件受力机理的异同点.基于此,对传统承载力叠加法的计算原理进行改进,通过数值模拟分析,验证改进后强度叠加原理的合理性和准确性.数值试验结果将用于评价在扭矩作用下钢管混凝土结构受力性能,同时可为进一步抗震性能研究打下良好的基础.

1 模型的建立及其有效性验证

本研究中混凝土的本构模型采用GB 50010—2010《混凝土结构设计规范》中提供的损伤塑性本构模型[7].混凝土的单轴受压应力-应变关系曲线如图1所示.

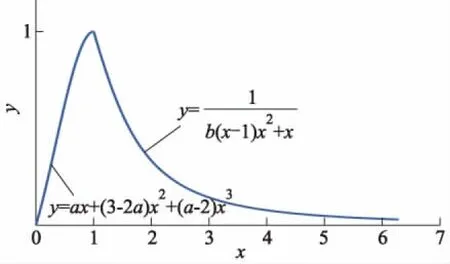
图1 混凝土单轴受压时的应力-应变曲线

关系式(1)为

(1)

混凝土的单轴受拉应力-应变关系曲线如图2所示.

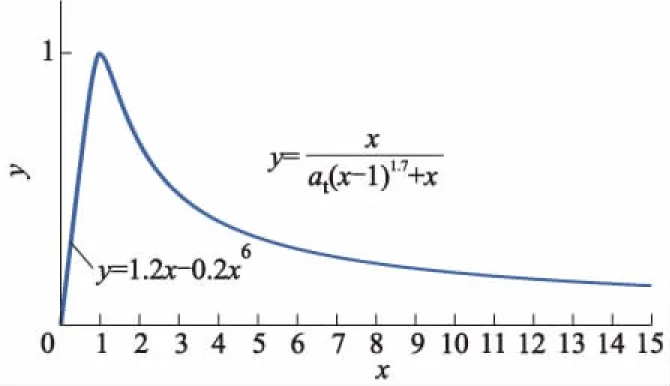
图2 混凝土受拉时的应力-应变曲线

关系式(2)为

(2)

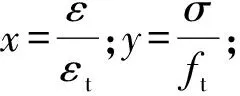
基于文献[7],本研究中钢筋的本构关系如图3所示.型钢的本构关系如图4所示.

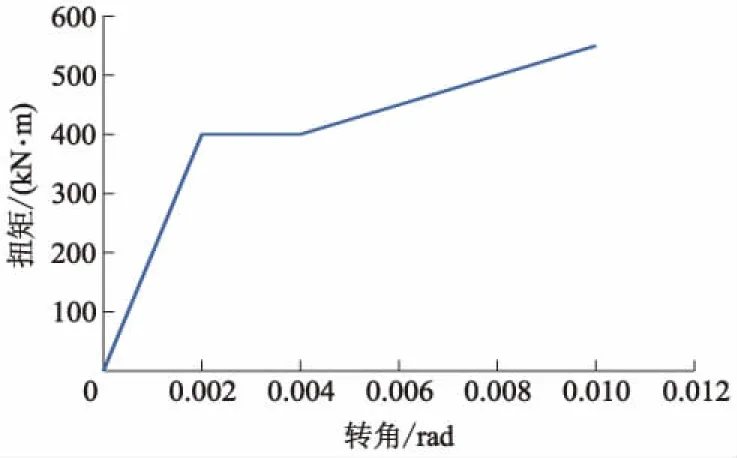
图3 钢筋的本构关系

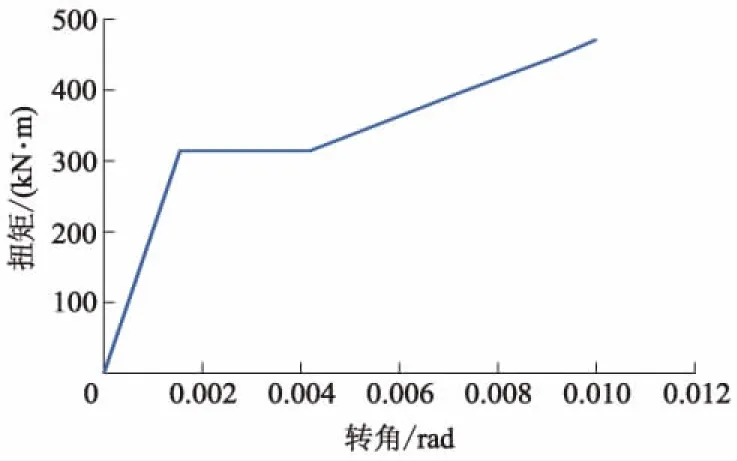
图4 型钢的本构关系

运用ABAQUS软件,在初始界面下分别建立混凝土、纵筋、箍筋及型钢部件,并对其材料属性进行定义.其中,混凝土与钢骨采用C3D8R单元;因钢筋只考虑沿长度方向的受力变形,故选用T3D2单元.通过Assembly模块将各部件组装成为一个整体构件,钢筋、钢骨与混凝土之间接触关系采用嵌入方式[8].

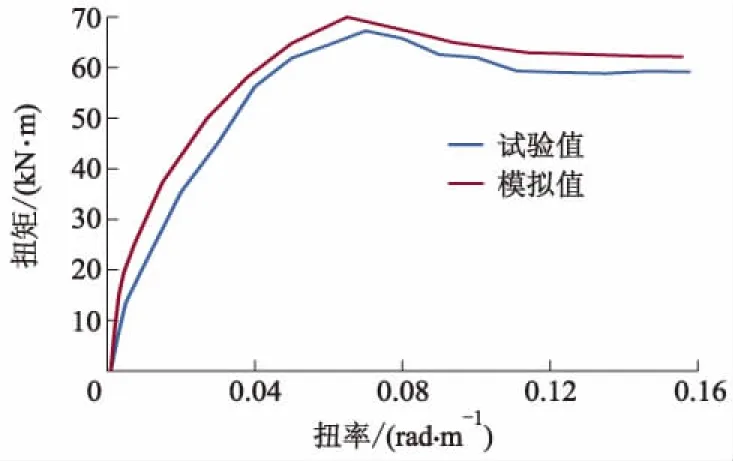
图5 扭矩-扭率关系曲线

2 试件设计及分组

为研究纯扭作用下箱型钢管混凝土构件各阶段

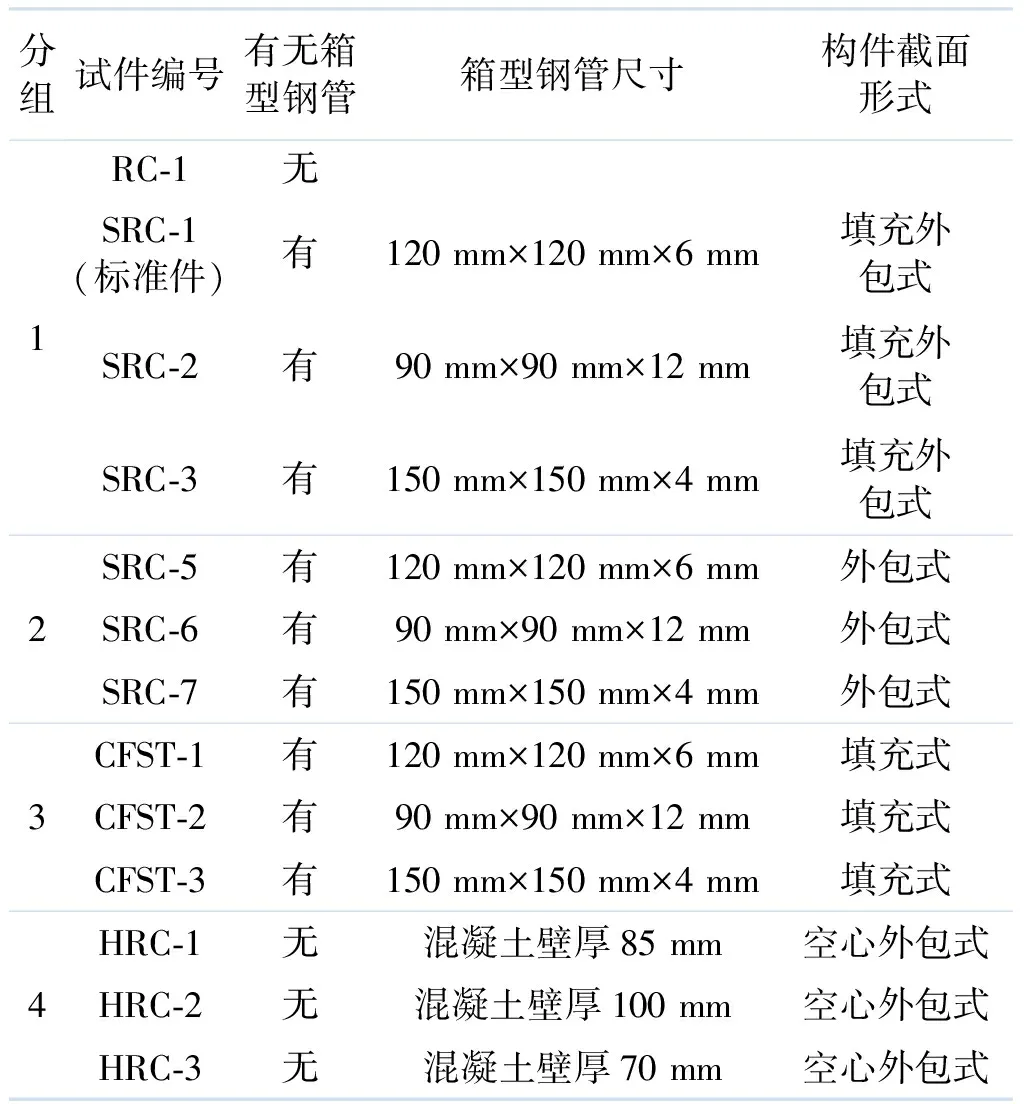
表1 模型试件参数

表2 构件材料参数

3 数值试验分析

3.1 纯扭作用下的应力分析

在ABAQUS的Visualization模块中,能够显现各个部件的应力云图,同时可以查看部件每个分析子步的应力云图.以试件RC-1,SRC-1和SRC-5为例,分析其受力过程.图6为3种构件开裂前混凝土应力云图,均为选取第1个分析子步的应力云图.由图6可知:3个构件开裂前的混凝土应力σ分布相似;纵观构件从未开裂到产生裂缝的过程中,Mises等效应力的峰值分布于截面边界的中间位置,最小值则在构件截面中心区域,表明构件在开裂前主要是由外包混凝土提供抗扭承载力,混凝土应力由边缘中间区域至截面核心区域的连线方向逐渐降低,核心区域所发挥的抗扭作用较小.

图7为RC-1,SRC-1和SRC-5试件破坏后混凝土的Mises应力云图.基于ABAQUS,可通过Mises等效应力或Max Principal了解裂缝的走向和分布情况.由图7可知:到达极限状态时,最大Mises等效应力分布是沿着试件长边与纵轴大致呈45°方向;从应力分布可知,SRC比RC具有更好的抗扭性能.

图6 开裂前混凝土的应力云图

图7 破坏后的混凝土应力云图

3.2 纯扭作用下极限状态时的应力云图

图8为极限状态时的钢筋应力云图.由图8a可知:RC试件开裂后,裂缝处混凝土部分退出工作状态,纵筋和箍筋组成的钢筋骨架开始参与到工作中;随荷载增大,裂缝开展情况逐渐加剧,钢筋对承受抗扭作用的贡献度在逐渐增大,裂缝位置处的钢筋首先达到屈服;随荷载继续增大,试件因受压一侧混凝土压碎而退出工作.

由图5也可发现,无论箱型钢管中间有无混凝土填充,箱型钢管的扭矩是基本相同.

图8 极限状态时钢筋应力云图

图9为试件SRC-1和SRC-5极限状态时型钢在xz方向的剪应力云图.通过对比图8a与图8b,8c,9可知:极限状态时两种试件型钢的部分剪应力分布相近,xz向最大剪应力为182 MPa,且将达到型钢的剪切屈服强度;试件在yz向和z向的剪应力云图变化相近,进而导致SRC试件纵筋尚未屈服,但部分箍筋达到屈服状态.由此表明:构件达到极限状态后,极限承载力主要由型钢及部分箍筋承受,因为箱型钢管抗扭刚度较大,导致其承担更多扭矩荷载;箍筋逐渐进入屈服状态,且其应变增长较快,纵筋因混凝土开裂,导致混凝土与纵筋黏结作用降低,因而纵筋所承受的扭矩作用较小.

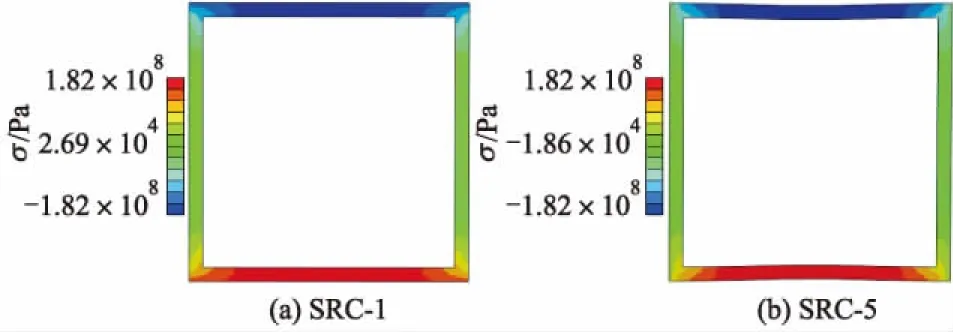
图9 极限状态时型钢在xz向剪应力云图

4 传统承载力叠加原理的改进

目前,国内外对于型钢混凝土受扭承载力的计算理论尚处于发展阶段,其中文献[10]提到的填充外包式混凝土柱构件叠加计算方法较为经典,计算公式为

TA=sTA+rTA,

(3)

式中:TA为容许扭矩,kN·m;sTA为钢筋混凝土部分容许扭矩,kN·m;rTA为钢骨容许扭矩,kN·m.计算原理示意图如图10所示.

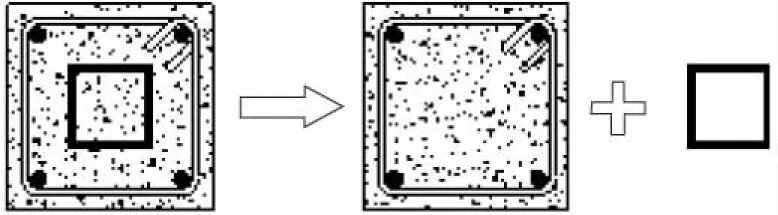
图10 计算原理示意图

对于纯扭作用下的箱型钢管混凝土构件的承载力计算,日本相关规范中提及的叠加方法存在不足之处,即在长期和短期荷载时,没有考虑到钢骨和钢筋混凝土之间的黏结应力传递相互间的剪力对抗扭承载力所带来的影响,而是由两者独立分担.

本研究基于传统的变角度空间桁架模型叠加法,以第2节中数值模拟结果为依据,将型钢混凝土等效为箱型钢筋混凝土和钢管混凝土的叠加,研究这种考虑钢骨部分和钢筋混凝土之间的黏结应力传递相互间剪力叠加方式的准确性.改进后计算原理示意图如图11所示.修正后承载力叠加原理计算公式详见文献[11].

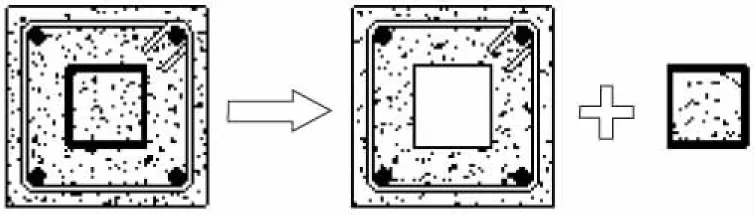
图11 修正后计算原理示意图

基于改进后的叠加法计算原理,对HRC试件、CFST试件、型钢及中空箱型钢管混凝土试件进行了数值模拟.图12为箱型混凝土试件HRC-1,HRC-2,HRC-3与RC-1的扭矩-扭率对比曲线.由图12可知:HRC试件与RC试件的曲线变化规律相近;随HRC试件内部空心尺寸增大,试件抗扭承载力逐渐降低,但抗扭承载力峰值相差较小,仅为4.2 kN·m;加载初期的HRC与RC均处于弹性状态,扭矩-扭率曲线呈线性变化;随外部荷载增大,试件开裂,并进入弹塑性阶段,试件内部空心尺寸越大,曲线切线斜率越小,但曲线最终都趋于平缓.综上,实心的钢筋混凝土试件与相同条件下空心箱型钢筋混凝土试件的抗扭性能近似等效.

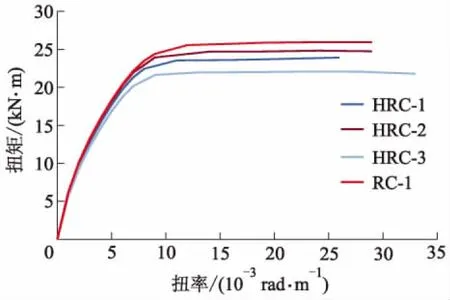
图12 HRC和RC的扭矩-扭率曲线对比

图13为试件CFST-1,CFST-2,CFST-3及型钢的扭矩-扭率曲线.由图13可知:CFST比型钢的抗扭性能高,其中CFST-3试件的最大扭矩提高5 kN·m;随着试件中型钢尺寸的减小,抗扭性能越接近.由此表明:箱型混凝土试件壁厚越大,核心区有无混凝土对其抗扭性能的影响越小;箱型混凝土试件壁厚越小,核心区有无混凝土对其抗扭性能的影响越大.

图13 CFST和型钢试件扭矩-扭率曲线对比

图14分别为SRC-1与SRC-5、SRC-2与SRC-6、SRC-3与SRC-7等3组外包填充式与外包式箱型钢管混凝土试件的扭矩-扭率曲线对比.

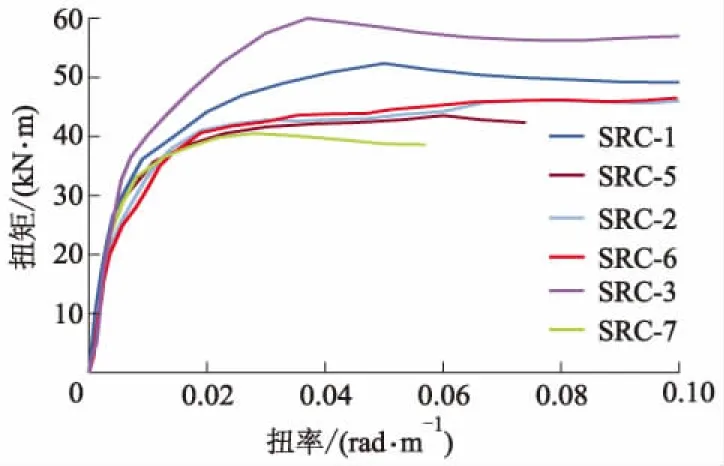
图14 外包式与外包填充式箱型钢管混凝土

由图14可知: SRC-1与SRC-5的抗扭承载力最为接近,SRC-2与SRC-6次之,而试件SRC-3与SRC-7相差最大.

分析原因可知:当试件SRC-7处于极限状态时,型钢混凝土部分受到外部混凝土约束作用,致使型钢向内严重屈曲不能正常地发挥其抗扭性能;SRC-3具有良好的抗扭承载力,型钢内部的混凝土能有效防止型钢向内屈曲,并保证型钢能够正常发挥其抗扭性能;由于试件SRC-7与SRC-3的差别之处是SRC-7无核心混凝土,因此型钢和混凝土之间的相互作用应予以考虑.

通过对比分析可以发现:随型钢尺寸减小,试件组SRC-3与SRC-7、SRC-1与SRC-5及SRC-2与SRC-6的曲线依次呈现出逐渐拟合到一起的现象,这表明随试件内部型钢尺寸减小(箱型混凝土试件壁厚增大),型钢本身抗屈曲能力逐渐增强,虽然没有混凝土的约束作用,也能有效抵抗屈曲,正常发挥抗扭性能.

基于钢筋、型钢和钢管等混凝土构件的抗扭理论,结合数值模拟,对改进后承载力叠加计算方法进行理论推导,并提出修正系数.改进后计算公式及修正系数详见文献[11].

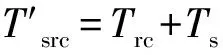
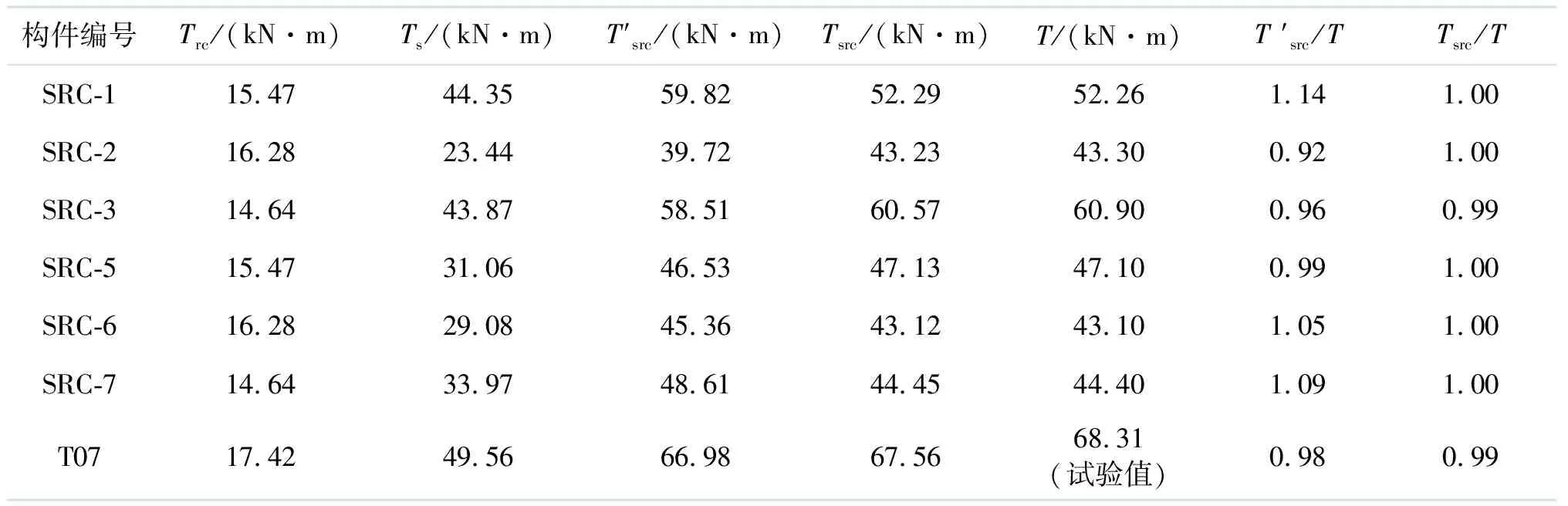
表3 极限扭矩模拟值与修正值对比

由表3可知:修正前的叠加值与模拟值最大误差为1.14,加入修正系数后,修正值精度有了很大提高,说明对修正系数的取值相对合理;本研究中选取文献[9]的一个T07构件进行验算,叠加值与试验值误差为0.98；加入修正系数后,修正值和试验值的误差比值提高到0.99,进一步验证了修正系数的准确性以及修正公式的合理性.

5 结 论

1) 基于ABAQUS对设计的13个模型试件进行数值模拟,将模拟结果与试验数据对比,验证了模型的有效性.

2) 试件开裂前,不同试件混凝土的应力变化相近,裂缝呈45°方向发展;试件达到极限状态时,型钢与部分箍筋基本达到屈服,纵向受力钢筋尚未屈服.

3) 根据对传统承载力叠加原理的探究,提出新型承载力叠加法.通过对比不同形式的箱型钢管混凝土试件的扭矩-扭率曲线,发现外包填充式箱型钢管混凝土构件具有良好的塑形性能,通过修正系数计算证明了改进后承载力叠加法的合理性和准确性.