基于MPI的近邻距离加权偏标记学习算法之并行实现

王 进, 高延雨, 邓 欣, 陈乔松

(重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065)

传统的监督学习方法[1]都是根据已有完整监督信息的训练集(即训练集中的样本都有精确的标记信息)建立分类模型,然后通过得到的分类模型对待测样本进行分类.但是现实中受外部环境、物理特性和物理资源等各方面状况的制约,有些场景很难得到完整的监督信息,例如对画作风格进行评定,不同的评定者因为知识和经验不同,对同一幅画可能有不同的评定结果,最终只能确定其属于哪几种风格,无法精确到具体的一种风格.仅知道训练样本标记候选集的场景可以使用偏标记的方法来进行处理.

偏标记学习[2-3]是一种重要的弱监督学习框架,具体定义如下:训练集中的训练样本对应多个标记,其中只有1个标记是真实标记,然后根据这样的训练集进行学习和对测试集的类别进行预测.目前,偏标记学习已经应用于多媒体内容分析[4]、网页挖掘[5]和人脸识别[6]等多个领域.

为了解决偏标记问题,一种常用的方法是对候选标记集合中的元素平等对待,将模型在各个候选标记上的平均输出作为模型输出,如基于K近邻的偏标记学习算法PL-KNN[7](partial labelKnearest neighbor)、基于凸优化的偏标记学习算法CLPL[8](convex loss for partial labels)等,但该方法构造之模型的性能受候选标记集合中伪标记的影响较大.IPAL[9](instance-based partial label learning)算法通过辨识消歧的方式克服了该缺陷,其分类性能优于多数的偏标记学习方法,该算法首先构建样本近邻的相似度图,然后通过迭代标记传播和CMN[10]方法对训练样本消歧,即实现每个训练样本只对应1个标签,最后对测试样本进行预测.

随着大数据时代的到来,大数据已经应用于网络安全[11]、人工智能和机器学习等多个领域.但IPAL[9]算法需要求取每个样本的K近邻,耗时特别多,而且该方法在构建近邻样本的相似度图时将求取每个样本近邻权值的问题转化为了有约束的最小二乘法问题,计算量较大,不适合处理大规模数据.

为了解决上述问题,笔者首先对IPAL算法求取近邻样本的方法进行改进,使用近邻样本间的距离替代有约束的最小二乘问题来求取近邻样本权值,提出基于近邻距离加权的偏标记算法WIPAL(weighted instance-based partial label learning).然后为了进一步提升WIPAL算法的运行速率,设计基于MPI的WIPAL算法的并行方法PWIPAL(parallel weighted instance-based partial label learning).通过试验对所提出的偏标记算法进行验证.

1 相关工作

MPI[12-14]是1个信息传递应用程序接口,适用于MIMD(multiple instruction multiple data)程序,也适合于更严格形式的SPMD(single program multiple data)程序,主要包括进程间通信、集合操作、进程组、通信上下文、进程拓扑结构、环境管理与查询等内容,进程间通信可以细分为点到点通信、组归约、广播、散射、收集、全交换等类型.MPI[14]具有高性能、大规模、可移植性、可扩展性等诸多优点,能够被C语言、C++和Fortran等编程语言直接调用,但MPI没有调试设施[15],因而开发难度较大.

偏标记学习[9]就是根据含有弱监督信息的训练集得到1个多类分类器.IPAL算法是一种基于样例的偏标记学习算法,主要由训练部分和测试部分组成,训练部分主要包括训练集相似度图的构建、迭代标记传播,测试部分包括测试集相似度图的构建和测试样本的预测.

相似度图的构建:本部分构建相似度图G=(V,E),其中V为样本,E用样本之间的相似度表示.首先根据样本之间的欧式距离求出训练集D中每个样本的K近邻,然后使用近邻样本重构其对应训练样本的方式获得近邻样本的权值,即

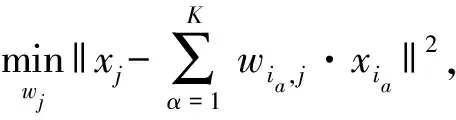
(1)

式中:xiα为xj的K近邻样本；wiα,j为样本xiα与xj之间的相似度;N(xj)为样本xj的K近邻样本索引集.

(2)

式中:yc为1个标记;Si为样本xi的候选标记集.

(3)

每一次标记传播结束后,根据实例的候选标记集合和计算式

(4)

最后每个样本根据标记置信度矩阵进行消歧,即将偏标记数据集转化为单标记数据集.在文献[9]中IPAL算法采用了CMN(class mass normalization)策略,使消歧考虑了各类别的先验分布,如下:

(5)

测试阶段:首先求得每个测试样本的近邻,然后根据最小重构准则求得每个测试样本与其近邻间的权重向量,算法根据测试样本近邻中的各类别对测试样本进行重构,重构误差最小的类别作为测试样本的预测标记,计算式为

(6)

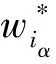
2 IPAL算法的改进

文献[9]的算法IPAL在求取近邻样本的权值、构建相似度图的过程中,采用近邻样本重构其对应样本的方法构建目标函数,将其问题转化为了有约束的最小二乘问题,但因训练集和测试集的每个样本需要处理有约束的最小二乘问题,耗时太多.为了解决该问题,文中提出了一种基于近邻距离加权的偏标记学习方法WIPAL.

鉴于IPAL算法中求取样本K近邻时已经求得了样本与其对应近邻样本之间的距离,根据样本之间距离越近、其类别相同概率就越大的思想,文中充分利用其已获得的近邻样本距离,将其近邻样本距离的倒数除以所有近邻样本的倒数之和所得的值作为近邻样本的权值,计算式为

(7)

式中Li,j为样本xi和xj之间的距离.处理有约束的最小二乘问题常采用迭代的方法,其时间复杂度为O(tpK(m+n)),式中p为样本特征数,K为近邻样本数,m和n分别为训练集和测试集样本数,t为迭代次数;基于近邻距离求取近邻权值的方法只需要对近邻样本的距离进行遍历就可获得其近邻权值,其时间复杂度为O(pK(m+n)).显然该方法的运算速度比文献[9]中处理有约束最小二乘问题获得近邻权值的方法快了很多.

3 并行算法PWIPAL

并行算法PWIPAL主要由读入训练集和测试集、构建训练集相似度图、迭代标记传播、读取测试集数据、构建测试集相似度图和测试样本预测等组成.

3.1 读入训练集和测试集

3.2 构建训练集相似度图

首先,开设c个进程,训练集特征D=[D0,D1,…,Dc-1],其中Di为第i个进程存储的训练集特征.每个进程采用轮询的通信方式将保存的训练集特征传播给相邻的进程,具体通信方式见图1,以4个进程为例,图1中方块中的数字表示进程号,箭头上的数字表示传播的训练集特征对应的进程号.

然后求取其进程自身保存的训练集样本特征与通信收到的训练集样本的欧式距离,保存K个最近的距离和其对应距离的索引,重复c-1次,每个进程就获得了训练集样本相对于整个训练集的K近邻,K近邻的索引存入各自的N中,其中N=[N0,N1,…,Nc-1].接着每个进程根据各自的样本及该样本对应近邻的距离,使用式(7)求得近邻样本的权值,将其存入W中.接着每个进程分别对对应的权值置信度矩阵进行量纲一化处理,结果保存到H中,量纲一化的方式是每个样本所对应的近邻的权值除以该样本对应的所有近邻的权值之和,即

(8)

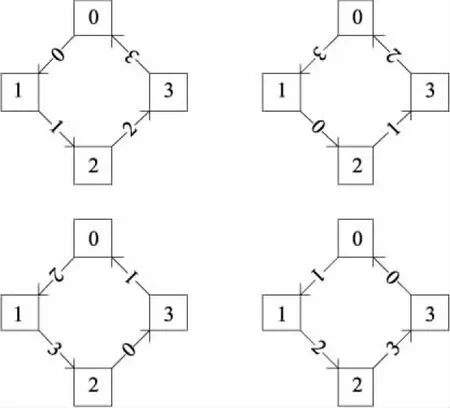
图1 轮询通信方式

3.3 迭代标记传播

3.3.1 迭代标记传播中计算改写

文献[9]在标记迭代传播的部分中,为了更新样本的标记置信度,需要计算权值矩阵乘以标记置信度矩阵,即式(3)中的HTF(t-1),原文中H是m×m的二维数组,其中H中每行最多有K个数,其余全部是0,K为近邻数,因此HTF(t-1)中有多处0与数相乘,造成了极大的计算资源浪费.一般的实现代码常使用稀疏矩阵来存储和计算,文中采用与稀疏计算类似的方法,用H来存储样本近邻的权值,这样H中每一行都有数值,不再稀疏;然后HTF(t-1)即样本的近邻权值与近邻对应的标记相乘然后求和,所以式(3)可改为

(9)

式中:hi,k为H中第i行第k列的元素;Ni,k为第i个样本的第k个近邻的索引.

3.3.2 并行迭代标记传播

首先,对于每个进程(以第i个进程为例)令训练集标签矩阵Pi=Yi,其中Yi为第i个进程的训练集标签.对Pi进行量纲一化处理,其方法与式(8)类似.令Fi=Pi,其中Fi为第i个进程的迭代标签置信度矩阵.

替代是翻译汉语文化负载词的一种有效方法。许多汉语谚语和典故在英语读者的认知系统中不存在，但它们可能有相似的表达方式。因此，译者可以找到一种相似的表达方式代替原有表达方式，从而达到更好的认知效果。

然后,每个进程根据式(9)和(4)进行标签置信度矩阵F的更新,如第i进程对Fi进行更新,在更新过程中采用轮询的通信方式,每个进程将自身的标签矩阵发送给相邻的进程,重复c-1次,对于整个更新过程重复迭代T次.

3.4 构建测试集相似度图

此部分采用与3.2节相同的方式构建相似度图,在其过程中每个进程保存了其样本对应的近邻样本的特征信息.

3.5 测试集样本的预测

每个进程采用轮询的通信方式将各自的训练集标签信息发送给相邻的进程,进而每个进程获得自身训练样本对应近邻样本的标签信息.接着每个进程分别使用各自测试样本的K近邻中各类别的特征根据式(6)对测试样本进行重构,重构误差最小的类别作为测试样本的真实类别.

通过对算法的分析得知并行算法PWIPAL算法的通信时间复杂度为O((2np+Tq)(c-1)/c),计算时间复杂度为O((n2p+nK(p+Tq)+mpK(n+1+q))/c),其中n和m为训练样本数和测试样本数,p为特征数,q为标签数,K为近邻数,T为迭代数,c为进程数;串行WIPAl算法的计算时间复杂度为O(n2p+nK(p+Tq)+mpK(n+1+q)).显然当n越来越大时,计算量比通信量增长速率高;当n无限大时通信量忽略不计,即开设c个进程,并行算法PWIPAL的运行速率比串行算法WIPAL快c倍,而且并行算法每个进程耗费的内存为串行算法的1/c,由此可见,PWIPAl算法可以处理大规模数据.

PWIPAL算法伪代码见下面,其中,Dr和Yr分别为第r个进程分到的训练集样本特征和标签.

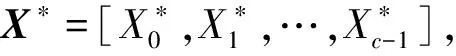
过程:

每个MPI进程r∈0,1,…,c-1启动

读取Dr,Yr

根据欧式距离和自身训练集特征获得Dr中每个样本的K近邻

Forj=1 toc-1 do

采用轮询通信方式,将Dr传播给其他进程,接收其他进程传递的训练集特征

根据现有的K近邻信息和收到的其他进程训练集特征更新Dr中每个样本的K近邻

End for

根据式(9)计算Dr的近邻权值矩阵Wr

根据式(8)对近邻权值矩阵Wr进行量纲一化处理

根据式(2)初始化标签置信度矩阵Pr

对Pr进行量纲一化处理,令Fr(0)=Pr

Fort=1 toTdo

Fori=0 toc-1 do

轮询通信方式将Fr传播给其他进程,获得其他进程的迭代标签置信度矩阵

根据式(9)和式(4)迭代更新Fr

End for

End for

根据式(5)和Fr对训练集样本进行消歧

Forj=1 toc-1 do

采用轮询通信的方式,将Dr传播给其他进程,获得其他进程的训练集特征

End for

Fori=0 toc-1 do

通过轮询通信的方式,将Yr传播给其他进程,同时获得其他进程的训练集标签

根据测试集样本的近邻索引,获得每个测试样本的近邻标签

End for

关闭所有的MPI进程

4 试验与结果

4.1 数据集

使用8个不同规模的UCI数据集和5个真实数据集进行对比试验,其中UCI数据集经过人工处理转换为偏标记数据集.将UCI数据集构造成偏标记数据集的处理方法如下:根据文献[5-6,8,16],使用参数p,r,ε控制生成的数据集,其中参数p控制数据集中偏标记训练样本的比例,参数r控制每个偏标记样本的伪标记个数,ε控制1个额外的偏标记与真实标记共同发生的概率.具体数据集信息见表1.

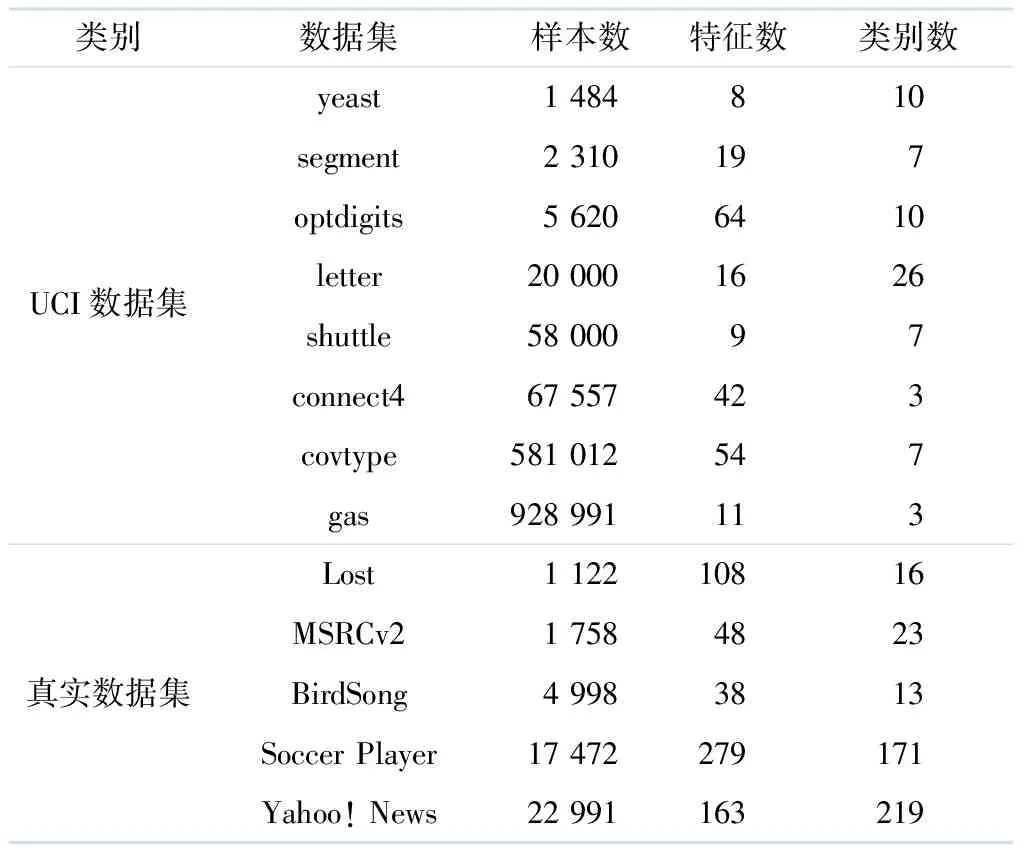
表1 数据集信息

4.2 试验环境

文中的并行试验在由8台服务器搭建的MPI集群上进行,串行试验在集群中的1台服务器上进行,集群中每台服务器的环境配置都如下:Cathe为15 MB,RAM为64 GB,Clock speed为2.0 Hz,CPU核心数为6,每个core支持双线程.操作系统为Centos 6.5,MPI版本号为3.1.4,GCC版本为4.4.7.

4.3 评价指标

文中将分类准确率、程序运行时间、加速比作为评价标准.其中分类准确率=预测正确的样本数/测试样本数,加速比=串行运行时间/并行运行时间.

4.4 试验结果与分析

本部分首先使用4个小规模的UCI数据集和5个真实数据集来验证算法WIPAL的分类准确率.将算法WIPAL与IPAL进行对比,试验中WIPAL和IPAL的平衡系数α=0.95,近邻数K=10,迭代次数T=100,求取K近邻时均采用线性扫描的方式.IPAL中使用开源库ipopt来解决有约束的最小二乘问题,HSL选择版本MA27.表2为UCI数据集中WIPAL与算法IPAL关于分类准确率的对比,其中ε=0表示不考虑偏标记与真实标记共同发生的概率.

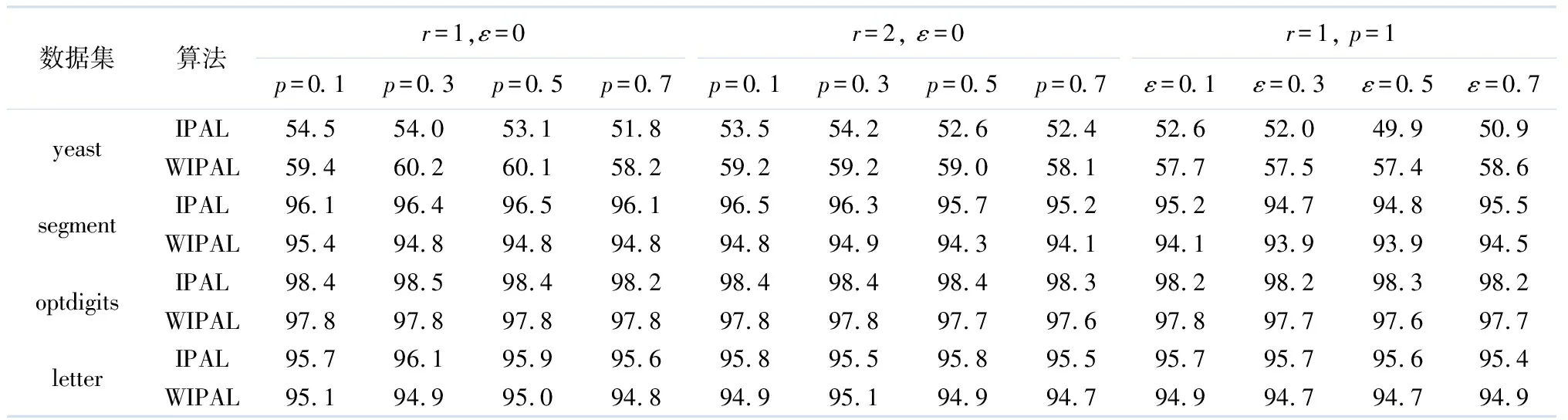
表2 UCI数据集分类准确率对比 %

由表2可见WIPAL算法的分类性能与算法IPAL相比有好有坏.表3为真实数据集中WIPAL与IPAL算法分类准确率的对比,由表3可见WIPAL算法在数据集Lost和Soccer Player上分类准确率性能优于IPAL,在其他数据集中,其分类准确率与算法IPAL相差很少.总体而言,WIPAL算法分类准确率与IPAL相当.

表4为在UCI数据集和真实数据集上算法WIPAl和IPAL关于运行时间的对比,UCI数据集的参数为r=1,p=1,其运行时间为十折交叉验证中一折的运行时间.

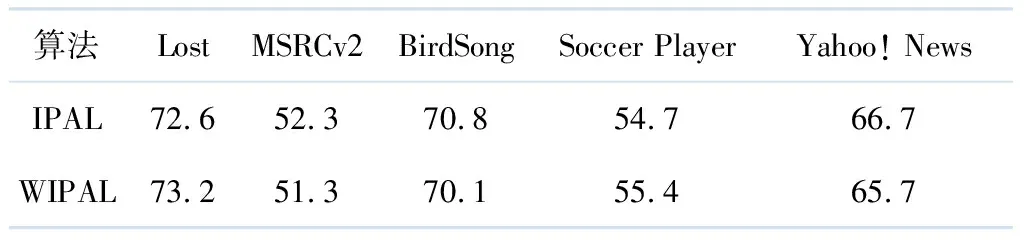
表3 真实数据集分类准确率对比 %

表4 运行时间 s

由表4可见在相同数据集的情况下，WIPAL算法运行时间较短,真实数据集的最后2个数据集中IPAL与WIPAL运行时间相差比例较小是因为这两个数据集比较大,IPAL和WIPAL计算每个样本近邻耗费的时间占据了总运行时间很大部分.为了测试并行算法PWIPAL的运行效率,文中选取了4个样本数规模从2万到90多万的UCI数据集,控制参数是r=1,p=1,通过设置不同的进程数进行对比试验,其运行时间为十折交叉验证中一折的运行时间,见表5,其中c为进程数.

表5 算法PWIPAL不同进程时的运行时间和加速比

由表5可见,对于数据集gas,当进程数由1增长为64的过程中,算法PWIPAL的运行时间逐渐缩短,由原来的18 677.41 s变为了389.82 s,加速比由1.00变为了47.91,根据数据集不变,进程数增加时，算法PWIPAL的运行时间和加速比可以看出对于相同的数据集,随着开设进程数的增多,PWIPAL的运行时间逐渐减少,加速比逐渐增多.根据数据集的不同规模可以看出,随着数据集规模的变大,在相同进程数时加速比在增多,例如当进程数为8时,数据集的加速比按照数据集规模递增的顺序逐渐增大.表中数据集shuttle在64个进程时运行时间变多是由于此时单个进程计算时间的减少量低于通信时间的增加量引起的.

5 结 论

首先对偏标记算法IPAL进行改进,提出了基于近邻距离加权的WIPAL算法;然后为了处理大规模数据,进一步提出了WIPAL的并行方法PWIPAL.在不同数据集下将WIPAL与IPAL的运行时间和分类准确率进行对比,得知WIPAL的分类准确率与IPAL相当,但运行效率要高于IPAL;然后在不同规模数据和不同进程数的情况下对PWIPAL的运行时间和加速比进行对比,验证了该并行算法的高效性,其可用来处理大规模数据.