HXD1组合列车牵引与电制动模型的验证
2018-11-15张帅,魏伟
张 帅, 魏 伟
(大连交通大学 交通运输工程学院, 辽宁大连 116028)
提速重载是我国铁路提高货物运输能力,降低运输成本的基本方向,在列车提速重载发展的同时,必然伴随着列车纵向冲动的增大。在列车运行时纵向冲动产生机理及操纵优化的研究中,目前常用的手段是对目标线路的列车运行过程进行实地测试,但实测取得数据的做法不仅耗费大量的人力物力,而且所得结果的通用性较差。因此通过建立列车模型采用仿真分析的方法对优化机车操纵方式,减小纵向冲动有着积极的意义。
张波[1]通过将HXD1机车牵引仿真计算与山区铁路襄渝线线路试验相结合,确定了合理的HXD1电力机车在长大坡道地段的牵引定数及针对下坡道电制动控速能力提出了合理建议;曹震[2]在分析列车编组、列车过分相以及列车制动等因素对重载列车牵引计算影响的基础上建立了牵引计算模型,对大秦线部分路段进行列车牵引运行仿真,用仿真结果与列车实际操纵对比分析验证了牵引模型的精度;耿志修[3]通过建立重载列车运行仿真计算模型,研究了大秦线不同编组重载列车的牵引、制动等技术参数,为大秦线组织重载列车试验,制订合理操纵方法等提供了技术依据;李曙辉等人[4]在充分考虑电力机车操作、运行特点及供电系统网压波动因素基础上,完成了SS3型电力机车的牵引运行仿真,结合实际线路,分析了网压对SS3机车运行特性的影响。
虽然众多学者对重载列车机车牵引仿真计算做了较多研究,但针对神朔铁路特有的线路环境,现有的牵引模型在描述神朔铁路HXD1万吨重载列车运行的准确性方面仍有待提高。文中根据神朔铁路实际运行情况提出新的机车牵引与电制动力学模型,完善了仿真程序TABLDSS[5-6],通过对神朔铁路部分路段进行列车运行仿真,将仿真结果与文献[7]中试验采集的相关数据对比分析来验证车辆运行基本阻力、牵引与电制动模型的准确性。
1 车辆运行基本阻力、机车牵引与电制动模型
HXD1型电力机车是株洲厂生产的用于牵引重载长大列车的干线货运机车,机车采用8轴双节重联,轴式为2(B0-B0),能满足长距离区间长大坡道上牵引重载长大编组货运列车运行的运输需要。
(1)车辆运行基本阻力模型
在原有车辆运行单位基本阻力模型[8]的基础上,文献[9]根据神朔铁路实际线路运行情况,利用蚁群算法,得到适用于神朔铁路的新车辆运行单位基本阻力模型如式(1)
(1)
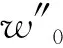
在25 t轴重下,HXD1机车牵引力及电制动力与机车速度的理论关系如式(2)
(2)
25 t轴重牵引特性
(3)
25 t轴重下,HXD1机车牵引力及电制动力与列车速度的理论关系特性曲线如图1和图2所示。
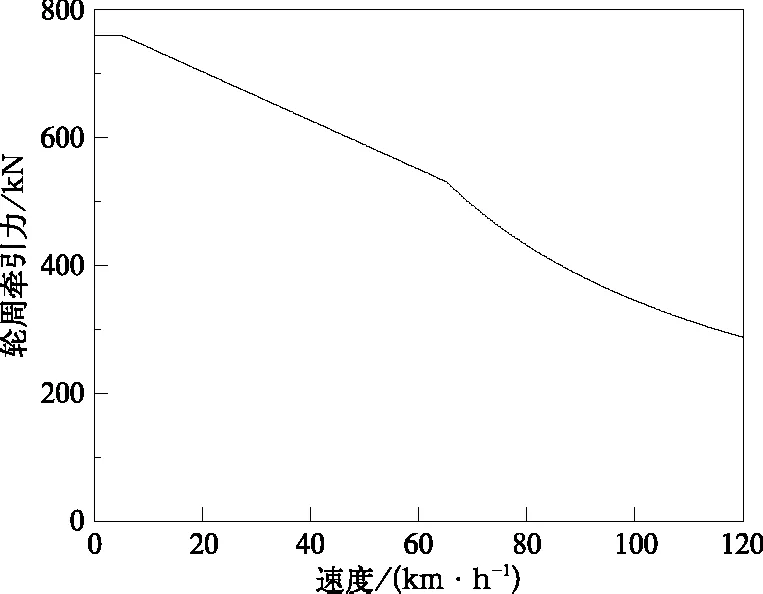
图1 HXD1牵引特性曲线
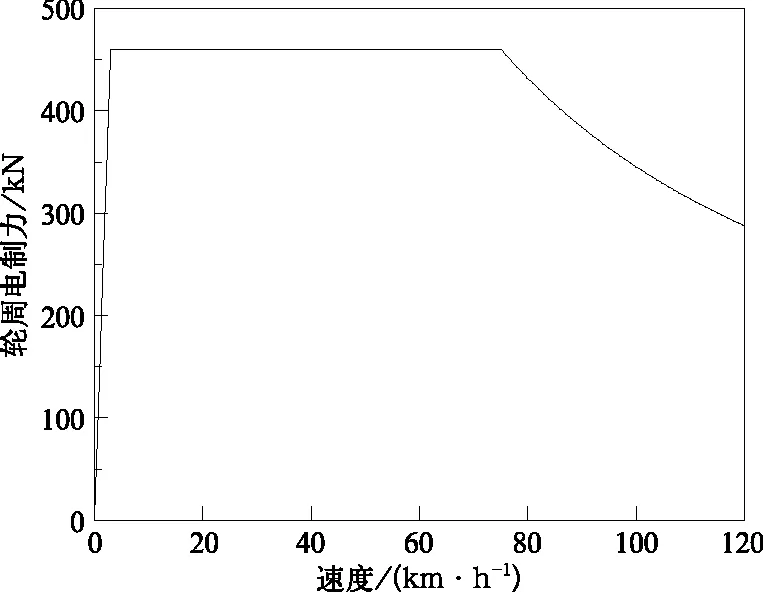
图2 HXD1再生制动特性曲线
在牵引力与电制动力理论关系公式基础上,考虑到网压变化的随机性[10]以及电机系统性能的不一致性,实际牵引力和电制动力的发挥与理论计算公式有一定的差异,故设置修正系数来建立更加符合实际情况的HXD1列车牵引与电制动模型如式(4)、式(5)
(4)
(5)
式(2)~式(5)中:Fmax、Bmax分别为机车最大牵引力和最大电制动力,kN;F、B分别为机车实际牵引力和实际电制动力,kN;IFmax、IBmax分别为机车最大牵引电流和最大制动电流,A;IF、IB分别为机车实际牵引电流和实际制动电流,A;k1、k2分别为牵引力和电制动力修正系数,该修正系数根据试验结果获得,均为常系数。
2 牵引与电制动仿真及试验验证
下面分别介绍了列车在惰行、上坡道牵引、下坡道电制动3种工况下的仿真、试验结果和比较分析,列车编组形式均为两辆HXD1+58辆C80+1辆HXD1+58辆C80(以下简称2+1编组)。
2.1 惰行工况
惰行行驶即在机车电动机不工作状态下,列车仅依靠惯性力运行,此时列车受力有运行基本阻力、坡道和曲线附加阻力。通过在该工况下模拟列车实际运行状态,比较分析仿真与试验的列车运行速度吻合程度,来验证车辆运行基本阻力模型的准确性。
而真实的情况是——有得必有失。Tina夫妇都是看重事业的人,追求更高职位的同时,也牺牲了夫妻甜蜜相处的时光。上司的一个电话就可能破坏了两个人的清闲周末,一次刻不容缓的业务谈判就推迟了早早制定好的出游计划。
神朔线18~21 km线路坡道变化如图3所示,列车惰行区间开始于18.195 km,在20.366 km处终止,全长2.171 km。该段线路下坡道最大坡度为-4‰,坡度为-1‰的最长坡道长度为1 km,平道长度200 m。
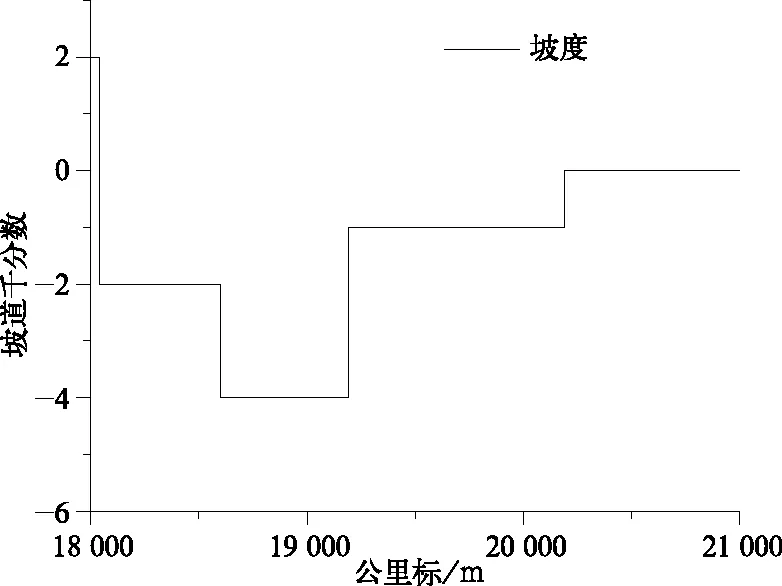
图3 神朔线路18~21 km坡道变化
列车在该线路区间运行时的速度曲线仿真与试验结果对比如图4所示:
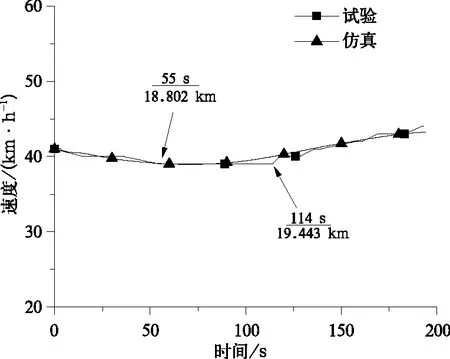
图4 列车速度曲线仿真与试验对比
在起始坡度为-2‰下坡阶段,此时坡道下滑力为列车提供前进方向力,但列车所受阻力之和大于坡道下滑力,因此列车减速运行,在55 s(18.802 km)处速度下降到最小值39 km/h;之后随着坡道坡度变为-4‰,速度开始逐渐增加。仿真的速度曲线在114 s(19.443 km)之前开始上升,上升开始时间比试验结果更早,分析原因可能是试验中此位置速度记录间隔过大,试验记录的速度不连续才产生较明显的阶梯变化。速度误差在114 s时最大为0.9 km/h。通过仿真速度曲线与试验对比分析,可以看出仿真与试验速度变化趋势基本一致,因此车辆运行基本阻力模型是比较准确的。
2.2 上坡道牵引工况
上坡道牵引工况下,列车受到机车牵引力、运行基本阻力及坡道和曲线附加阻力共同作用,在新车辆运行阻力模型已经被验证准确的基础上,通过模拟列车在上坡道牵引工况下的运行过程,比较分析仿真与试验速度、车钩力等特性参数的吻合程度,来验证列车牵引力模型的准确性。
神朔铁路44~51 km行驶区间坡道变化如图5所示,上坡道牵引工况下,列车从44.041 km开始运行,结束于50.148 km,全长6.107 km。在该线路区间内,1.5‰坡道持续1.5 km,之后在0.4 km内坡度从1.5‰快速增加至10.9‰,最后的4.1 km列车完全在坡度>10‰的长大上坡道运行。该段线路坡度变化明显,机车主要以牵引方式运行,因此截取该段线路进行上坡道牵引仿真与试验比较研究。试验所获得的机车在该线路对应位置牵引电流变化情况如图5所示,牵引电流在44.107 km开始施加,44.303 km处增至320 A,持续到45.860 km开始连续下调至290 A,之后继续增加,在47.366 km达到最大值480 A,保持恒定直至运行过程结束。
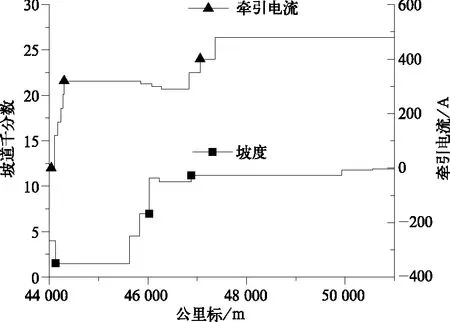
图5 神朔铁路44~51 km坡道 状况/牵引电流指令变化
列车在该线路区间运行时的速度曲线仿真与试验结果对比如图6所示,牵引电流在机车运行前14 s(前200 m内)很小,机车牵引力小于列车所受阻力之和,因此列车速度下降;37 s时(44.549 km处)牵引电流由120 A增至320 A,坡道坡度仍为1.5‰,此时牵引力大于列车所受阻力之和,因此列车速度增加;在37~96 s间,仿真速度增加速率较试验略大,调查试验数据发现这是由于从控机车牵引电流较主控机车略小的缘故,仿真与试验速度最大差值出现在58 s(44.854 km)位置,速度误差为1.0 km/h;在158~350 s间,坡道坡度从10.5‰增加至11.8‰,牵引电流从290 A增至480 A,速度基本恒定在69 km/h,可以看出仿真模拟出的速度变化趋势、峰值与试验吻合很好。
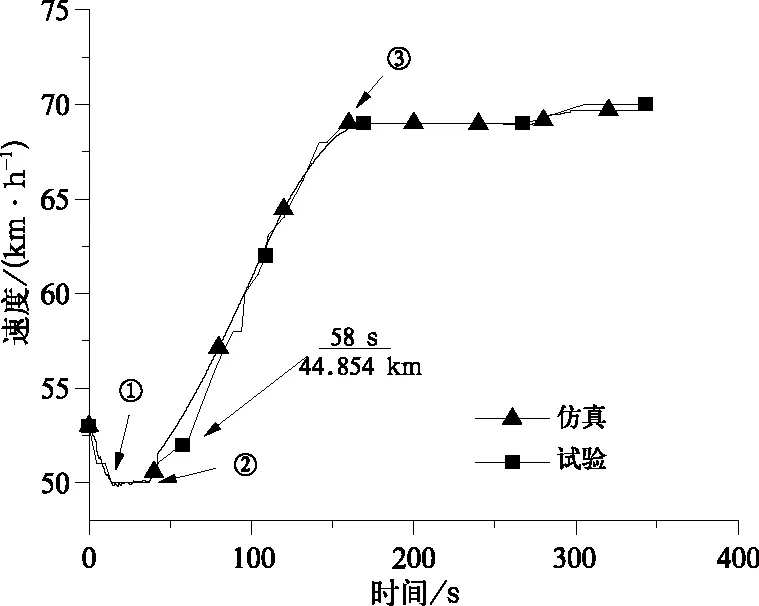
图6 列车速度曲线仿真与试验对比
选取图6中14,37和158 s关键时间点的列车位置、速度参数与仿真结果对比如表1所示,可以发现仿真与试验在同一时间点,位移误差最大为12 m,速度最大相差0.7 km/h,误差均很小。
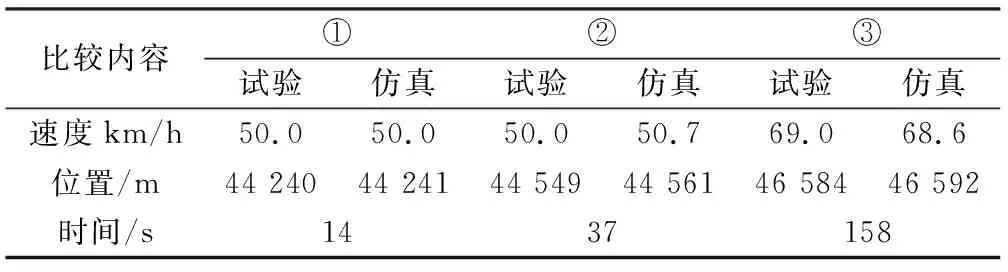
表1 试验与仿真结果关键点参数比较
第4车车钩力时域曲线如图7所示,车钩力整体表现为拉钩力(用“+”表示),仿真结果变化趋势与试验结果基本一致。车钩力均在30 s(44.464 km)左右上升到第一个尖峰达到662.6 kN;此时牵引电流320 A,坡道坡度最小为1.5‰,之后随着牵引电流减小到290 A,车钩力开始下降,在169 s(46.788 km)处降至446 kN;在变坡点46.880 km处,坡度由10.5‰增至11.2‰,此时牵引电流由290 A增至350 A,车钩力开始增加,在238 s(48.099 km)达到最大值881 kN;此后牵引电流维持在最大值480 A,坡道坡度为11.2‰,车钩力稳定于最高峰值。在210~230 s内,仿真较试验缺少一个匀速再上升的变化过程,车钩力最大差值28 kN,误差比为3.2%,分析原因可能是由试验记录的该段牵引电流指令缺失引起。
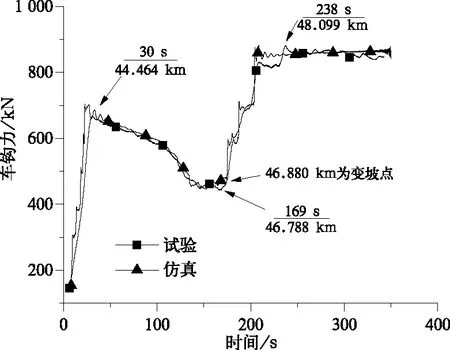
图7 第4车车钩力曲线仿真与试验对比
为了研究上坡道牵引状态下拉钩力随列车车长的变化规律,绘制了最大车钩力沿车长分布曲线如图8所示,并将数值结果及误差列于表2中。
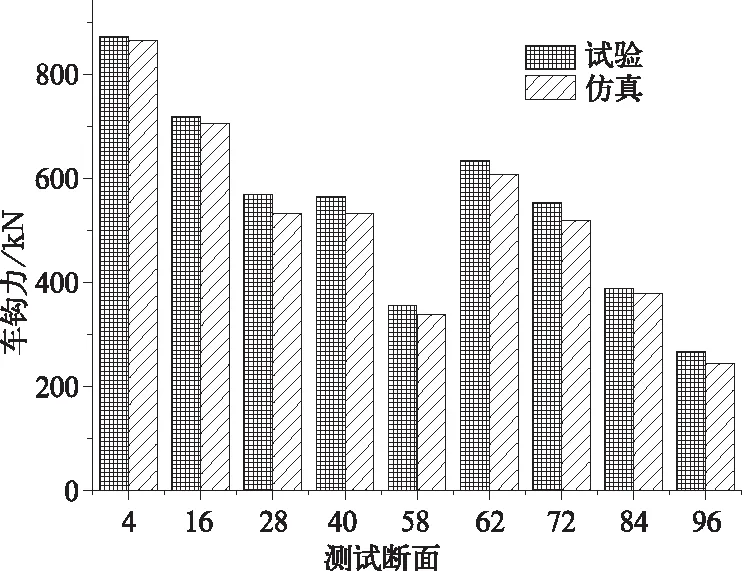
图8 各断面测试车辆最大车钩力变化

车位41628405862728496试验车钩力/kN881.0719.7569.9565.0356.0634.0553.0388.2267.0仿真车钩力/kN865.8706.5531.8533.0337.0607.0519.0379.5243.0差值比值%+1.7+1.8+6.7+5.7+5.3+4.2+6.1+2.1+8.9
可以看出车钩力从第4车到第58车呈递减趋势,这是因为牵引力与牵引质量相关,车钩越靠后,牵引质量越小,导致车钩力越小;第62车车钩力相比第58车出现骤增,原因是从控机车位于第62车前,从控机车提供牵引力,所以车钩力在62车位出现增加,之后再逐渐递减,直至最后一辆车,车钩力传递规律与文献[11]所得结果基本一致。仿真车钩力数值在9个车位上均略低于试验车钩力,最大差值出现在第96车位,误差为8.9%。由此可以看出本仿真程序所模拟的HXD1(2+1编组)列车在上坡道牵引工况下的车钩力与试验吻合很好。通过以上比较分析,可以认为文中建立的列车牵引力模型是比较准确的。
2.3 下坡道制动工况
下坡道选取神朔铁路27~32 km线路,此段线路坡道变化如图9所示,列车运行起止区间为27.487~31.397 km,全长3.91 km。区间线路起始坡度为-2‰,列车行驶155 m后进入坡度为-3‰的坡道,运行600 m后在线路28.242 km处进入500 m长的坡度为-1‰坡道,之后在28.786 km开始在长达2.35 km的最大坡度值为-4‰的下坡道运行。此段线路坡度整体变化平缓,机车主要使用电制动控制车速,因此截取该段线路进行电制动工况下仿真与试验对比分析。试验机车在该线路对应位置制动电流变化情况如图9所示,制动电流在28.640 km处开始施加,在30.444 km增加至最大值350 A,之后在30.821 km处开始逐渐下降,直至运行区间结束。
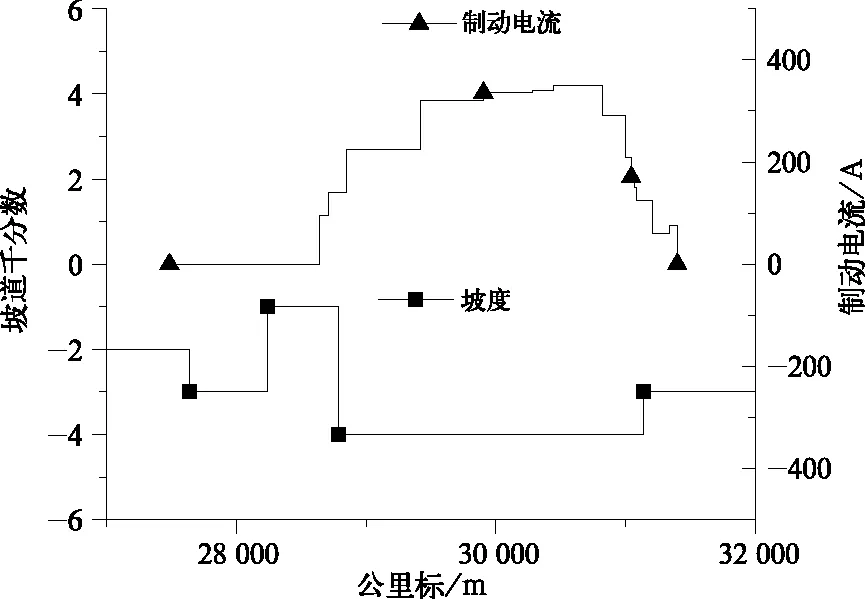
图9 神朔线路27~32 km坡道变化/制动电流变化
机车在该线路区间运行时的速度曲线仿真与试验结果对比如图10所示,对比分析发现,在运行前78 s (28.817 km前),坡道坡度主要为-3‰,机车无电制动指令,列车速度缓慢增加至最大速度62 km/h;之后出现了短暂的匀速运行过程,这是因为机车电制动力、列车所受阻力与坡道下滑力的合力随着坡度从-3‰减缓至-1‰而出现受力平衡,因此列车由加速变成匀速运行;在78~300 s(28.817~31.043 km)间,坡道坡度由-1‰变为-4‰,制动电流由140 A连续增加至350 A,列车速度由62 km/h减至12 km/h.此过程中主要通过调节机车制动电流值,使列车的电制动力和列车所受阻力之和大于坡道下滑力,实现列车下坡道减速运行;行驶到300 s (31.043 km)处,坡度由-4‰变为-3‰,制动电流由210 A减到170 A,速度开始保持不变。仿真与试验速度在运行过程中最大差值出现在336 s(31.155 km)位置,大小为0.8 km/h,误差较小。
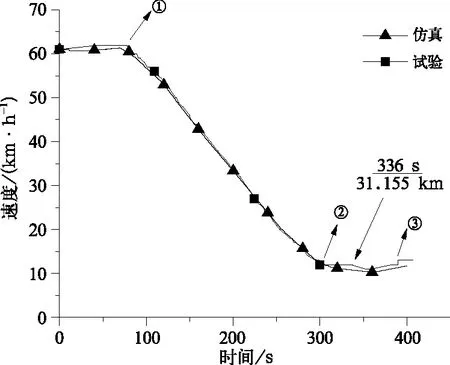
图10 列车速度曲线仿真与试验对比
选取图10中78,300和390 s关键时间点的列车位置、速度参数仿真与试验对比如表3所示,位移最大误差17 m,速度最大误差0.7 km/h,可以看出关键时间点的各项参数吻合很好。
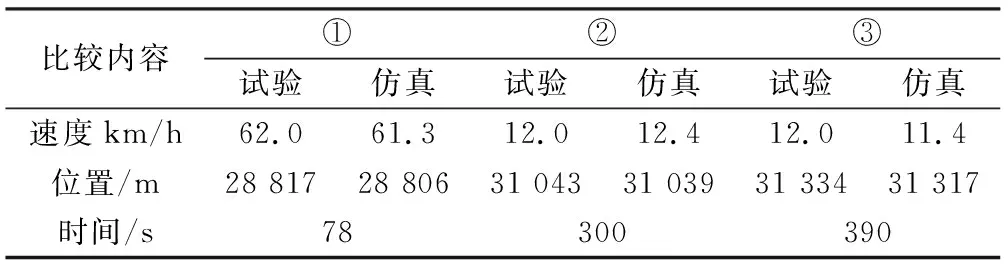
表3 试验与仿真结果关键点参数比较
第4车车钩力时域曲线如图11所示,电制动工况下车钩力整体表现为压钩力(用“-”表示)。在机车运行前50 s内车钩力基本为0 kN。在50~250 s(28.413~30.821 km)坡度由-1‰变到-4‰,制动电流由0 A逐渐增至350 A,车钩力开始增加;在90 s时间点试验车钩力出现10 s的稳定,仿真车钩力此时虽有微小震荡,但回稳后趋势与试验基本一致;在210~250 s间,仿真车钩力与试验相比缺少下降再上升变化过程,分析原因可能是由该位置试验记录的制动电流指令缺失导致。在250~350 s之间,车钩力随着制动电流的减小出现阶段性下降,其中289~325 s仿真车钩力曲线与试验相比提前上升,已知此段坡道坡度、制动电流指令不变,分析原因是仿真过程中存在的速度误差使列车于原定试验时间前到达牵引电流指令变化位置,制动电流作用从而导致车钩力提前增加。仿真与试验车钩力最大差值出现在229 s(30.687 km),误差大小为3.7%,可见第4车仿真车钩力变化趋势、峰值点与试验吻合很好。
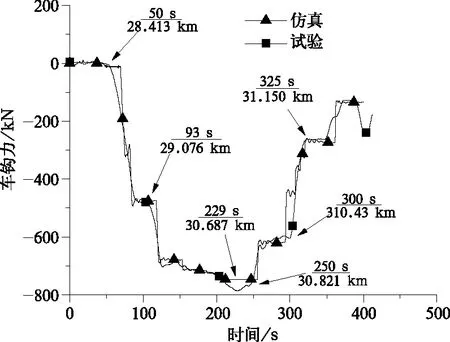
图11 第4车车钩力曲线仿真与试验对比
为了分析下坡道电制动状态下压钩力沿列车车长的变化规律,绘制了最大车钩力沿车长分布曲线如图12所示,并且将数值结果及误差列于表4中。从图12和表4可以看出,较大压钩力出现在主控和从控机车的后一个车辆位置,第4车车钩力在数值上与机车电制动力最为接近,之后再逐级递减,在第58车达到最小值;第62车相比第58车压钩力明显增大,是因为中间机车同时施加电制动作用的缘故,然后车钩力再从第62车依次递减至最后一辆车。车钩力最大差值出现在第84车位,最大误差-10.5%。通过以上对比分析,可以看出本文建立的列车电制动力模型是比较准确的。

表4 各测试断面最大车钩力试验与仿真结果对比
3 结 论
结合列车牵引计算理论,通过建立机车牵引与电制动力学模型,分别验证了惰行工况、牵引工况、电制动工况下仿真系统中车辆运行基本阻力、牵引与电制动模型的有效性。
(1)在惰行工况下,仿真的列车运行速度变化与试验对应的测试值吻合较好,本仿真系统能够很好地模拟HXD1电力机车(2+1编组)惰行工况下的运行情况,证明了车辆运行基本阻力模型是准确的;
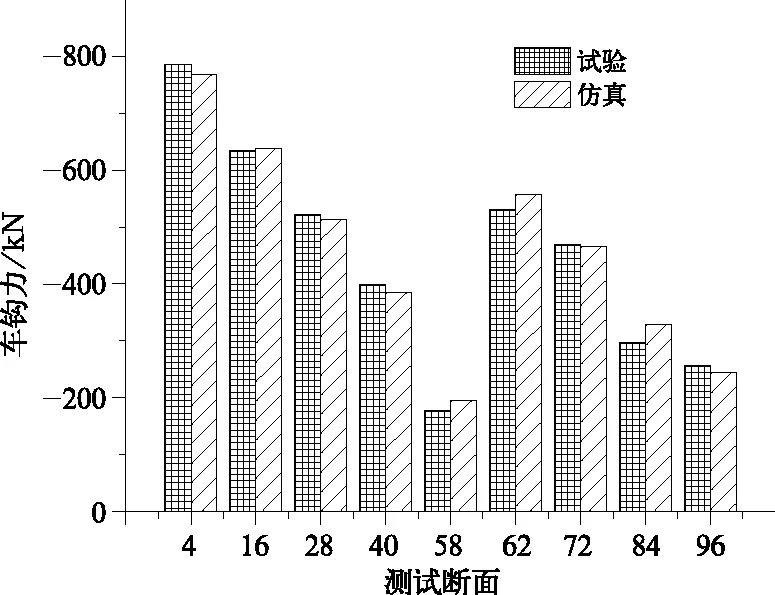
图12 各断面测试车辆最大车钩力变化
(2)在上坡道牵引工况下,列车运行的速度、车钩力变化等特性参数均与实际试验对应的测试值吻合较好,本仿真系统能够很好地模拟HXD1电力机车(2+1编组)在上坡道牵引工况下的运行情况,证明了所建立的列车牵引力模型是准确的;
(3)在下坡道电制动工况下,仿真运行的速度、车钩力变化等特性参数均与实际试验对应的测试值吻合较好,本仿真系统能够很好地模拟HXD1电力机车(2+1编组)在下坡道电制动工况下的运行情况,证明了列车电制动力模型是准确的。
