基于等值渗流阻力的非均质油藏水驱前缘计算
——以非洲R油田为例
2018-11-14周春香黄强强
周春香,夏 林,黄强强
(1.中国石油大港油田勘探开发研究院,天津 300280;2.渤海钻探油气合作开发公司,天津 300280)
确定注水井水驱前缘的推进状况对油田的开发和调整具有重要的意义。目前确定水驱前缘位置的方法有贝克莱-列维尔特法、试井分析、微地震、数值模拟方法等[1-5]。这些方法或不考虑储层非均质性对水驱规律的影响或因求解过程复杂,难以准确定量描述水驱前缘推进距离,本文基于油水两相等值渗流阻力理论,在考虑储层纵向非均质性基础上,对水驱前缘推进距离进行定量刻画,并预计井组的见水时间。
1 R区块基本地质特征及开发存在的问题
R区块位于非洲某油田,该区储层物性好,电测解释孔隙度为19%,渗透度为330 mD,为中低孔高渗储层,地下原油黏度为1.9 mPa.s,地面原油密度为0.85 g/cm3,属常规轻质油,储层非均质性强,渗透率极差为4.9,变异系数为0.7。投产初期采用反九点井网天然能量开发,投产4年后转注水开发,受高速开发及政治因素影响,油藏初期采油速度高(3%),油水井纵向上均多层合采合注,吸水剖面测试资料分析纵向上层间吸水差异大,单层突进现象严重,有必要开展注水井水驱前缘推进状况研究,预测油井见水时间,采取合理的控水稳油调整措施。
2 水驱前缘计算模型
2.1 基于油水两相等值渗透阻力的水驱前缘计算
实际油藏由于岩石微观非均质性、油水性质差异及毛管力现象,在油水接触前缘后,一直到含油边界原始位置的地方,存在油水混合的两相渗流区。根据物质平衡原理,生产井见水时刻的总采出油量应该等于从供给端到采出段地层中含油的减少量[6]。已知累计产出量大小,即可由注水时对应的时间,求出任意时刻t对应的水驱前缘推进距离rφ:
(1)
(2)
式中rφ——油水两相过渡区半径,m;
h——油层有效厚度,m;
Φ——孔隙度,小数;
δ——孔隙利用系数,小数;
Q——生产井总采出油量,m3;
q——含义,任意时刻t时采出油量,m3;
t——油井采出油量对应时间,d;
Swi——束缚水饱和度,小数;
Sor——残余油饱和度,小数;
zφ——油水接触前缘可动油饱和度,小数。
根据油水两相等值渗流阻力设计理论,对于面积注水井网,认为每口注水井周围形成的油水两相过渡区为圆形,过渡区半径为rφ。以反九点面积注水系统为例,一口注水井或三口生产井的产量及压降计算如下[7-8]:
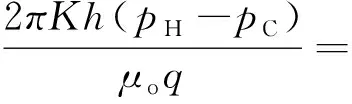
(3)
式中K——有效渗透率,mD;
pH——地层压力,MPa;
pC——井底流压,MPa;
μo——油黏度,mPa·s;
roi——油井半径,m;
row——供给边界半径,m;
a——注水井到最近生产井的距离,m;
μr——油水黏度比,小数。
利用公式中的油水接触前缘可动油饱和度zφ和油水两相过渡区半径rφ,通过试凑法可计算任意时刻的油水两相过渡区半径,即得出任意时刻t的水驱前缘推进距离。
而与rφ值对应的时间t由下式确定:
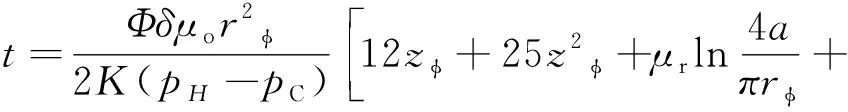
(4)
2.2 计算结果
以R区块中心1注8采反九点井网为例,井网内2口边井为单向受益井,2口井均合采3个小层,利用上述计算方法得出不同阶段油井水驱前缘推荐距离,从R4-12井和R4-14井可看出,生产第44个月水驱前缘半径分别为439 m、356 m,此时R4-12井生产见水,R4-14井尚未见水(表1)。
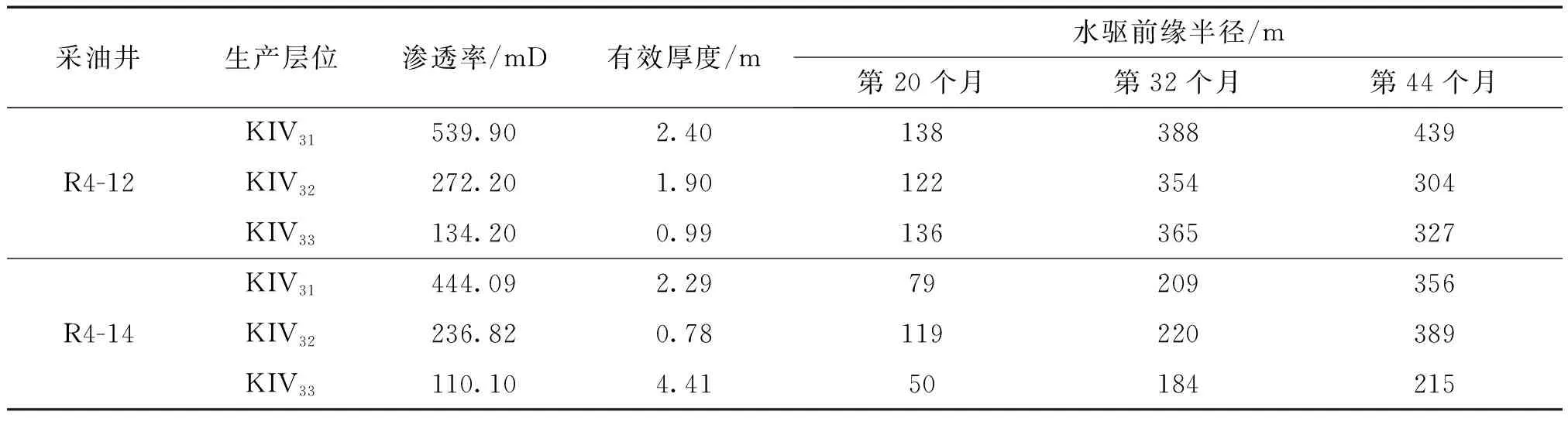
表1 油井分阶段水驱前缘半径计算Table 1 Leading edge radius at different stages
3 计算结果验证与适应性分析
3.1 数值模拟计算及预测
根据油藏精细描述结果,利用Eclipse数值模拟软件建立R区块油藏数值模型[9-10],对储量和生态动态进行历史拟合,预测不同时间步的水驱前缘推进距离和采油井见水时间。
提取注水开发第20个月的KIV31单砂层剩余饱和度平面图和R4-12井-R4-13井-R4-14井连井剖面图(图1),从剩余油分布图上看,第20个月油井R4-12井及R4-14井均未见水,水驱前缘推进距离分别为150 m、100 m左右;剖面上看,纵向上各小层吸水不均衡,KIV31小层水驱推进速度快,其他层推进速度慢。由提取注水开发第32个月的KIV31单砂层剩余饱和度平面图和连井剖面图(图2)可见,油井R4-12井已见水,R4-14井未见水,水驱前缘推进距离分别为400 m、250 m。由提取注水开发第44个月的KIV31单砂层剩余饱和度平面图和连井剖面图(图3)可见,油井R4-12井、R4-14井均见水,水驱前缘推进距离分别为450 m、300 m,其中R4-14井水驱前缘并未推进至生产井底,含水主要受边水影响。数值模拟论证结果与水驱前缘计算模型、生产动态吻合度高。通过模型可进一步预测R4-9、R4-11井见水时间为第86个月、60个月左右。
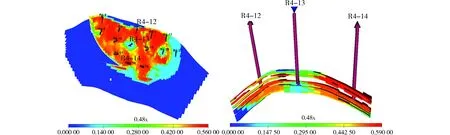
图1 第20个月剩余油饱和度Fig.1 Residual oil saturation plane and profile diagram at the 20th months
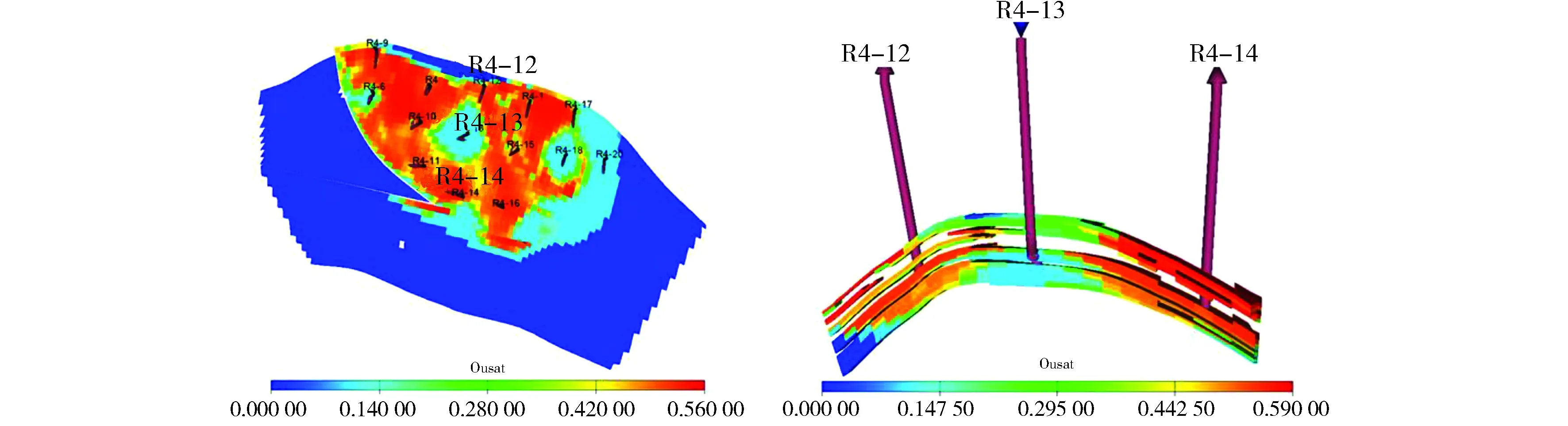
图2 第32个月剩余油饱和度Fig.2 Residual oil saturation plane and profile diagram at the 32th months
图3 第44个月剩余油饱和度Fig.3 Residual oil saturation plane and profile diagram at the 44th months
3.2 适应性分析
本文所列公式(3)生产井的产量与水驱前缘计算公式仅针对反九点面积注水系统。另外从数值模拟结果及油水井生态动态上看,R区块东部油井受注入水和边水双重影响,含水上升快,判断R区块东部存在弱天然水体,利用该方法计算边部油井水驱前缘推进距离,可能导致计算结果偏小。为了避免计算偏差,物质平衡方程式中应考虑天然水驱水倾量的影响。因此本文计算方法适用于天然能量较弱、反九点井网开发、储层物性相对较好、注水为单向驱替的水驱油藏。
4 结论
(1)基于油水两相等值渗流阻力设计理论,推导出反九点面积注水系统水驱前缘计算模型。
(2)在多层可采的情况下,储层层间非均质性差异影响水驱前缘推进距离,物性较好的储层水驱前缘推进速度快。
(3)文章所述方法可定量计算单向注水受益油井任意时刻的水驱前缘推进距离,经油藏数值模拟和生产动态证实,计算结果可信度高,该结果对于预测油井见水时、及时开展井网及注采剖面调整具有重要意义。
