基于小波变换的图像融合算法比较研究

王华兵 邱春荣 宫蓉蓉

（长沙民政职业技术学院，湖南长沙410004）

1.引言

来自于不同信息源的同一研究对象的图像具有信息冗余性和互补性，图像融合技术能够有效地将这些多源图像进行各个角度的合成，从而提高图像的清晰度、可读性和信息量。研究者们运用不同的数学理论和工具开展了许多理论和实践探索，并提出了许多图像融合的实现技术。常用的图像融合技术有：加权平均法、拉普拉斯变换法、小波变换法（Wavelet Transform，WT）等[1]。小波变换是一种基于短时傅里叶变换发展起来的变换方法。该方法克服了傅里叶变换局部信息和非平稳信号分析能力弱的局限性，通过变换突出图像的局部特征，并通过伸缩平移方法实现信息的多尺度分解。因此，小波变换在图像处理、语音识别、计算机视觉等领域得到了广泛的应用。小波基函数是实现小波变换的基础性条件，而小波基函数具有不唯一性，常见的小波基函数有Haar函数、Symlets函数、Biorthogonal函数、Meyer函数、Daubechies函数等。

本文基于小波变换的不同基函数和分解尺度调整，在MATLAB平台上得到多源图像信息融合的不同合成图像，并应用灰度均值、标准差、信息熵、平均梯度等四个评价指标进行图像融合的质量对比，从而得出不同小波变换图像融合算法的多维度性能结果。

2.相关工作

应用小波变换的信息融合主要有两种思路。第一种是改进小波变换的信息融合算法。文[2]对小波变换分解出来的高频和低频系数进行不同的组合，根据结构相似度和图像边缘算子构建出新的融合算子，并实施信息融合得到了性能较好的融合图像。李俊峰等[3]对小波变换分解的低频和高频信息进行加权融合，并根据噪声含量的不同设计了区域梯度能量融合方案。叶明等[4]根据小波变换后分解出来的低频子图和高频子图，利用不同的融合系数进行图像融合。李伟等[5]应用第二代小波变换的Lifting方案，提出了基于区域特征选择的融合算法，得到了较为简单高效的图像融合效果。徐小军等[6]针对小波变换图像融合算法中的伪吉普斯效应，应用离散分数阶小波变换（DFRWT）提出了分数阶小波变换（FRWT）算法。第二种思路是改变小波变换的基函数和分解尺度，探索出融合效果更好的图像融合算法。何宏[7]、李敏[8]应用Haar函数对不同频率分量的图像融合效果进行了仿真实验对比分析，提出了有效的小波变换融合方法。张彬等[9]则应用Biorthogonal函数对红外和可见光图像开展了信息互补融合实验，并利用Biorthogonal函数的对称性和良好的滤波特性，提出了效果良好的GMP图像融合算法。

上述研究成果从不用的角度探索了小波变换的信息融合方法及其效果，但鲜有研究对不同基函数和分解系数的小波变换图像融合进行比较实验分析和效果对比。

3.小波变换图像融合及其评价指标

3.1 小波变换图像融合算法

小波变换始于1974年，是工程师在信息处理过程中通过经验总结出来的反演公式。小波变换通过时频变换来实现特征信息提取的目的，并利用伸缩运算和平移运算实现对工程信息的多尺度分析。其定义公式为：

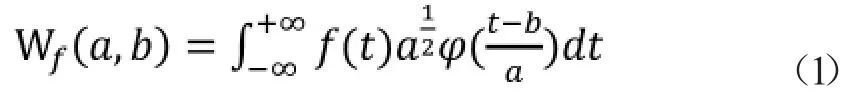
式中f(t)是一维信号，φ(x)是小波基函数，而a、b分别表示伸缩系数和平移系数。

由式（1）可知小波基函数直接影响到小波变换的结果，常见的小波基函数有：

（1）Haar函数

Haar函数是一个矩形波，支撑域的范围为，其定义如式（2）所示。

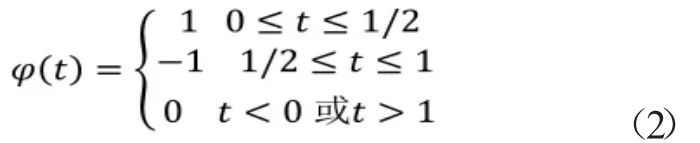
（2）Daubechies函数

Daubechies函数又可以表示为dbN，其中N表示小波函数的阶数。该基函数的支撑区为[0,2N-1]，没有具体的表达式，但转换函数h满足如下计算式：

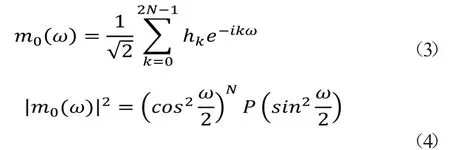
（3）Symlets函数

Symlets函数是对Daubechies函数基础上进行改进的一种近似对称小波函数，它保持了Daubechies函数的简单性，同时增加了对称的特征。其表示形式为

（4）Biorthogonal函数

Biorthogonal函数即双正交小波函数，具有线性相位特性，主要应用于信号重构领域，通常做法是使用一个函数进行分解，而另一个函数进行重构操作，表示方法为biorNr.Nd，其中Nr为重构函数，Nd为分解函数。

（5）Meyer函数

Meyer小波函数是在频域中定义的正交小波，其定义式如式（5）所示：

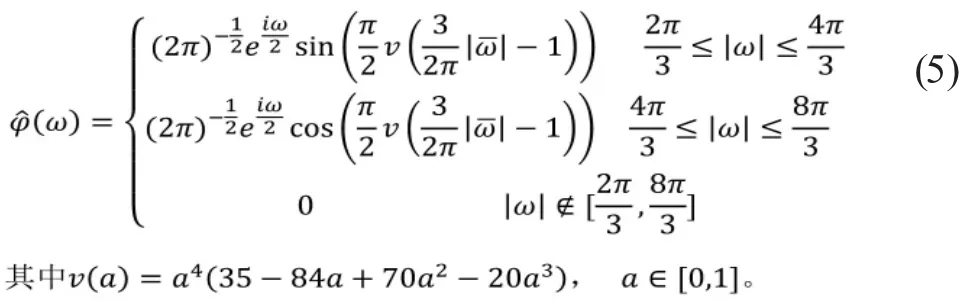
3.2 图像融合评价指标

从单张图像的信息量、清晰度、统计特性等角度来分析，图像融合的常见评价指标有：均值（ME）、标准差（STD）、信息熵（E）、平均梯度（AG）等。下面分别阐述这四个评价指标[10-11]。

均值是指图像所有像元的灰度算术平均值，其定义公式如（6）所示。

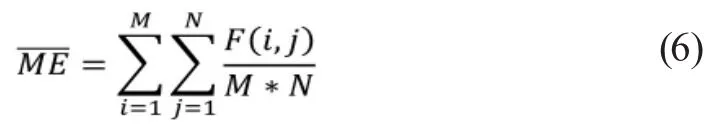
其中M、N分别表示图像F（M、N）的水平和垂直大小尺寸，和分别像元F（i,j）的位置。

（2）标准差（STD）

图像标准差是指图像灰度相对于灰度平均值的离散程度。标准差越大，表示图像的灰度级越分散，图像对比度越大，图像特征越明显。反之标准差越小，则意味着图像色度越均匀，对比度小，图像特征信息不明显。其定义如式（7）。

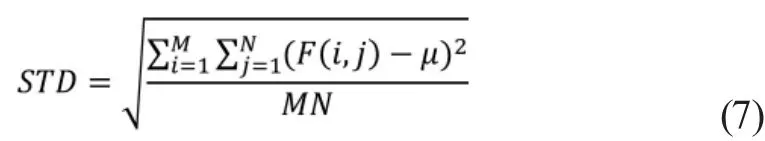
其中μ表示图像均值，F(i,j)表示图像在位置(i,j)的灰度值，图像尺寸为M*N。

（3）信息熵（E）

信息熵表征了图像所包含的信息量的大小，其表达式如式（8）所示：

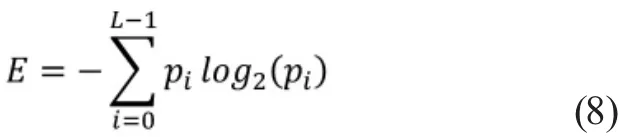
其中L表示图像的总灰度级数，i表示灰度值，Pi表示像素数量Ni与图像总像素N的比值。对比图像融合前后的信息熵，就可以衡量图像融合前后信息的增加量，从而判断图像融合的质量。

（4）平均梯度（AG）

该指标是指图像对像元细节特征的表达能力。平均梯度可以反映图像的清晰度和纹理变换特征，其表达式如（9）式所示。

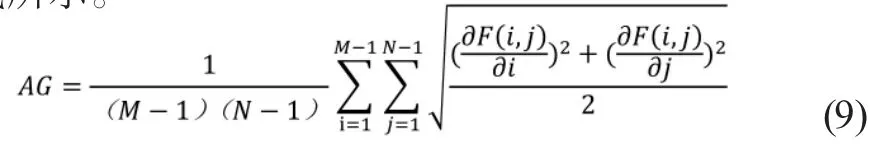
其中M、N分别表示图像F（M、N）的水平和垂直分辨率，i和j分别像素F（i,j）的位置。平均梯度越大，表示图像越清晰。

4.实验结果分析

实验选用两种同一角度但清晰程度不同的图像，分别用 Haar、db4、sym4、bior、meyer五个函数进行图像融合，并调整分解层级系数为4和8，共得到图像融合结果图像10张。对10张融合图像计算得到灰度均值（ME）、标准差（STE）、信息熵（E）、平均梯度（AG）等四个指标评价，并进行结果分析，实验平台为MATLABR2010a。如图1所示。

从图1可以主观地判断图像融合的效果。从图像局部来看，各种小波变换函数融合后的图像视觉质量均得到了明显提高，源图像1左下角区域和源图像2的右边区域清晰度有了较大程度的改善。各种小波变换函数之间的融合效果从直观上区分效果不太明显，经放大后可以初步判断10张融合图像中相对较好的有Db融合图像（分解层级为4）、Haar融合图像（分解层级为4）、Db融合图像（分解层级为8）等。其它融合图像难以从直观上加以判别。

图1 源图像及融合图像

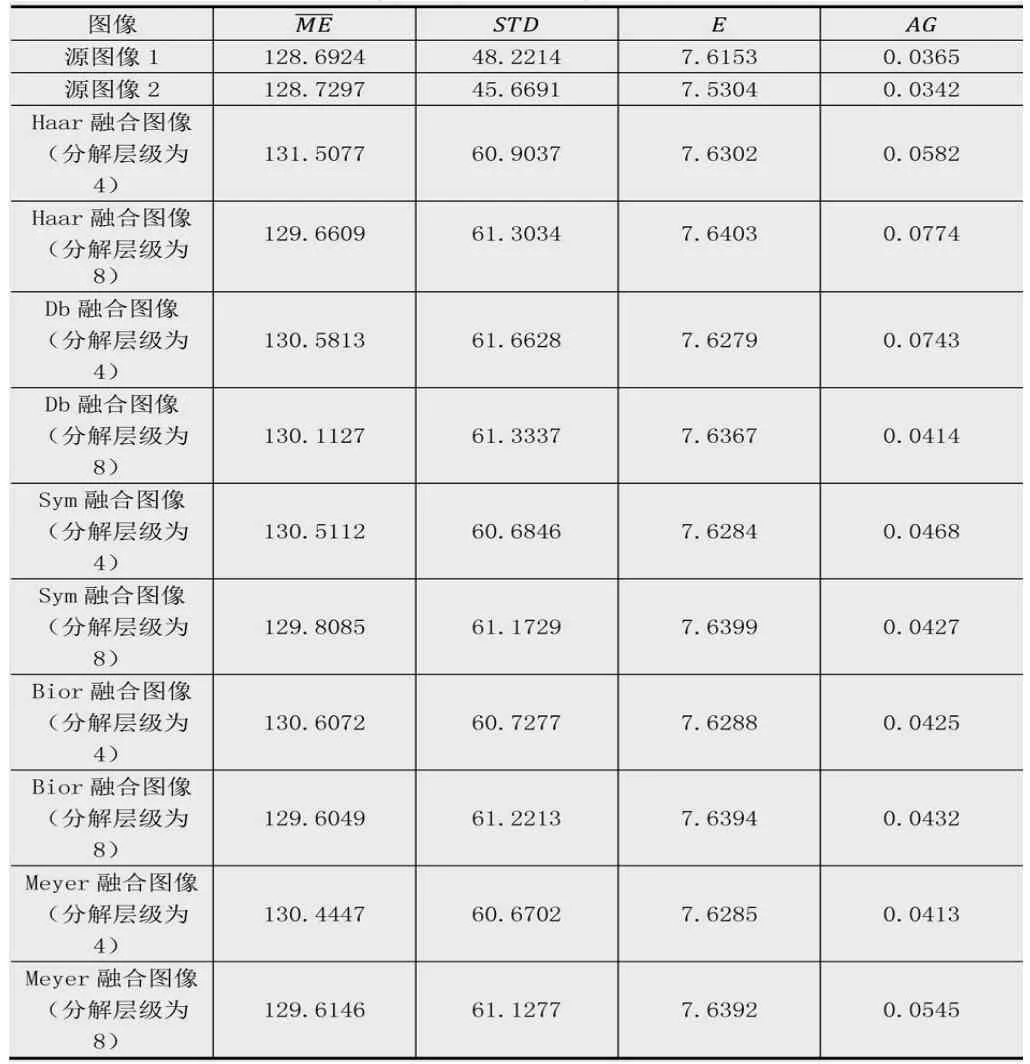
表1 源图像及融合图像的质量评价

5.总结

小波变换是图像信息融合的常用方法。本研究从调整小波基函数和分解层级入手，分析了五种小波基函数及其不同分解层级的融合效果。实验结果表明：（1）Db融合图像（分解层级4）、Haar融合图像（分解层级4）、Db融合图像（分解层级8）等三种小波变换图像融合方案具有较好的效果；（2）分解层级的提高与图像融合效果的改善没有必然的联系。后续的研究包括其他小波基函数的图像融合实验，分解层级逐级对比分析，小波变换与其他工具结合应用的图像融合效果分析等。