真实入口条件下隔离段内激波串迟滞回路现象研究

骆红朱，金志光，张堃元

(南京航空航天大学 能源与动力学院， 南京 210016)

作为高超声速进气道的重要组成部件，隔离段在进气道与燃烧室之间起着气动热力缓冲作用，不但能隔离燃烧室对进气道的干扰，为进气道提供较宽的工作范围，并且可以实现超燃冲压发动机在不同工作模态之间转换[1]。隔离段内流动十分复杂[2]，在下游燃烧室反压作用下，隔离段内部是一系列以激波/边界层相干扰为主要特征的减速增压过程。其中激波串结构长度、总压恢复特性、抗反压能力很大程度上决定隔离段的尺度与工作性能。

P.J.Waltrup等[3-4]针对一维轴对称等直圆管进行了激波串特性试验，给出了管内增压比与激波边界层相干长度的关系式。B.F.Carroll等[5-6]对矩形管内的激波串结构进行了数值模拟与试验研究，证实该公式也适用于矩形管道，其试验结果被广泛用作数值模拟的验证算例。

在国内，袁化成等[7]研究了反压作用下的等直隔离段性能，给出了均匀来流条件下等直隔离段最大承受反压时隔离段长高比选取的拟合式。张航等[8]对进口斜激波、膨胀波干扰下等直隔离段内的激波串特性进行了研究，得到了出口反压和激波入射位置对激波串的影响，虽然考虑了进口激波的影响，但是进口条件给定的方法与真实条件下隔离段进口偏差较大。王渊[9]完善并研究了非对称来流下的矩形转圆隔离段设计方法。陈植[10]，易仕和[11]结合精细流动测试技术的发展对隔离段内流动特征进行了细致研究。曹学斌等[12]在国内进行了考虑进气道喉道非均匀流场影响的隔离段直连试验，完成了壁面沿程静压、纹影和非接触式NPLS激光测量，获得了一些试验数据，但试验过程中未能保证隔离段入口参数相同，因此具有一定的局限性。目前为止，考虑真实入口条件下隔离段内流动特性的研究较少。

本文利用真实入口条件隔离段简化模型，研究了考虑进口激波/膨胀波以及非对称边界层干扰下隔离段隔离段内激波串特性，并与均匀来流情况进行了对比。

1 研究模型及计算方法

1.1 研究模型

图1为典型马赫数(Ma)在4～6范围工作的进气道-隔离段模型。外压段总压缩角为15.5°。此模型由于内压段唇口斜激波与肩部膨胀波的交替反射会在隔离段入口形成复杂的非均匀流场结构，势必会对下游隔离段内的激波串特性产生影响。

为了方便地模拟隔离段不同入口条件下的非均匀流场结构，截取上述进气道模型内压段下游结构，同时增加前体边界层发展长度，形成如图2所示的真实入口条件下的隔离段简化研究模型。

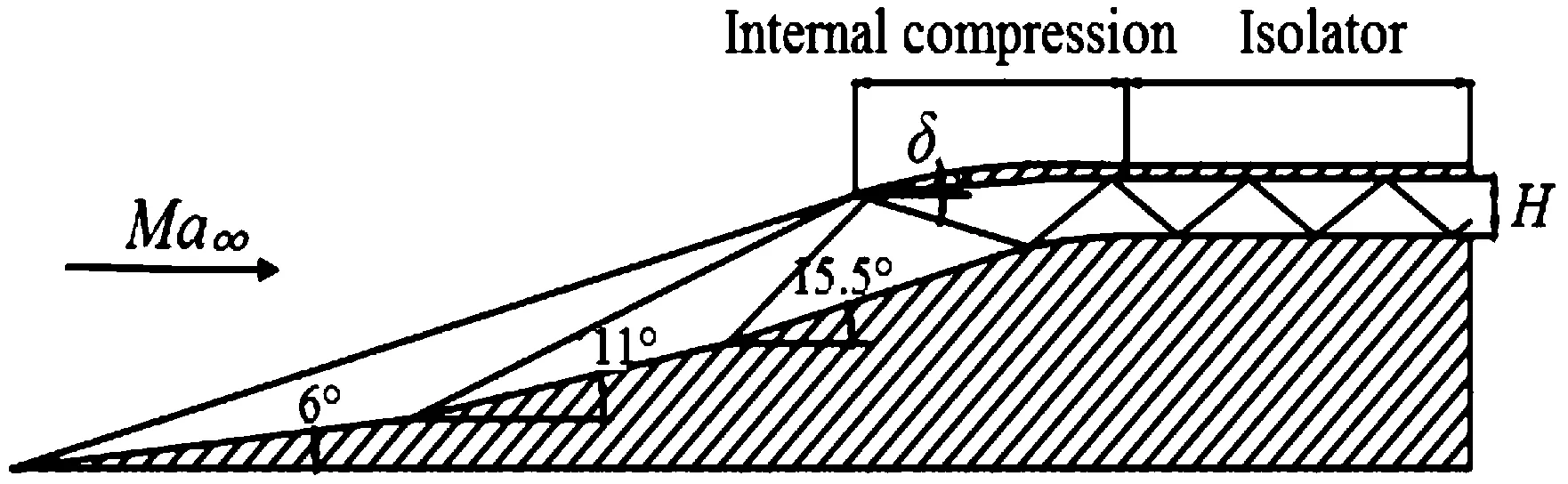
图1 进气道-隔离段模型简化

该模型来流方向与前体平行，隔离段入口流场不受进气道外压段波系配置影响，在保证进气道喉部(隔离段入口)平均参数不变的前提下，通过改变内压段设计，同时配合来流马赫数的变化能获得与各种进气道设计方案相对应的隔离段真实入口流场结构。

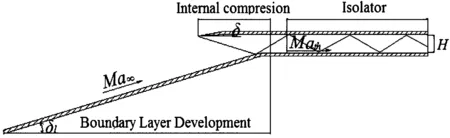
图2 真实入口条件下隔离段简化模型

基于这种模型，喉道高度H为48.2 mm，隔离段长度L为7倍喉道高度，隔离段入口选在距等直段1倍喉道高度处，选取内收缩比CRin为2.26，唇口角度δ为3°，内压段长度L1/H为5.81。在对应于进气道Ma4工况下研究了真实入口条件下隔离段内激波串特性，并与均匀入口条件下的隔离段性能进行了比较。均匀入口条件：隔离段为带边界层发展段的等直隔离段。表1给出了来流参数，其中隔离段入口马赫数Math为2.11。

表1 隔离段模型远场来流条件

1.2 计算方法与算例验证

划分网格时对边界层近壁面及激波根部进行局部加密处理，第1层网格高度0.001 mm，增长因子1.15，保证壁面y+小于1，总网格量约14万。边界条件采用无滑移绝热壁面、压力远场和压力出口。

采用Fluent软件进行数值计算，黏性方程为k-ωSST模型，采用Sutherland公式计算分子黏性系数，使用二阶迎风格式离散方程对流通量采用Roe-FDS格式计算，收敛依据：各残差下降到0.001且进出口流量差在0.001 kg/s以下并保持稳定。

为了验证上述数值计算方法可靠性，对文献[13-14]中的进气道/隔离段模型和Carroll在文献[5]中给出的试验结果进行数值仿真并与试验结果进行对比验证，模型的几何参数和来流条件均依据文献中的试验条件设定。图3给出了隔离段长度为79.3 mm，自由来流马赫数为2.5，隔离段出口为自由无反压状态时计算、试验结果对比。可以看出：所用数值计算方法能够清晰地模拟出唇口激波的形态和位置，并且均与试验吻合得较好。此外，将隔离段上下壁面压力分布与试验数据对比，发现与试验比较吻合。

图4给出了来流马赫数为1.61、边界层厚度与管口半高之比为0.32时的计算、试验结果对比。可以看到数值模拟能够较准确地捕捉到激波串形态，且数值模拟获得的壁面静压分布与试验数据吻合良好。因此，说明本文所使用的网格划分策略和数值计算方法能准确模拟出隔离段内流动状态。

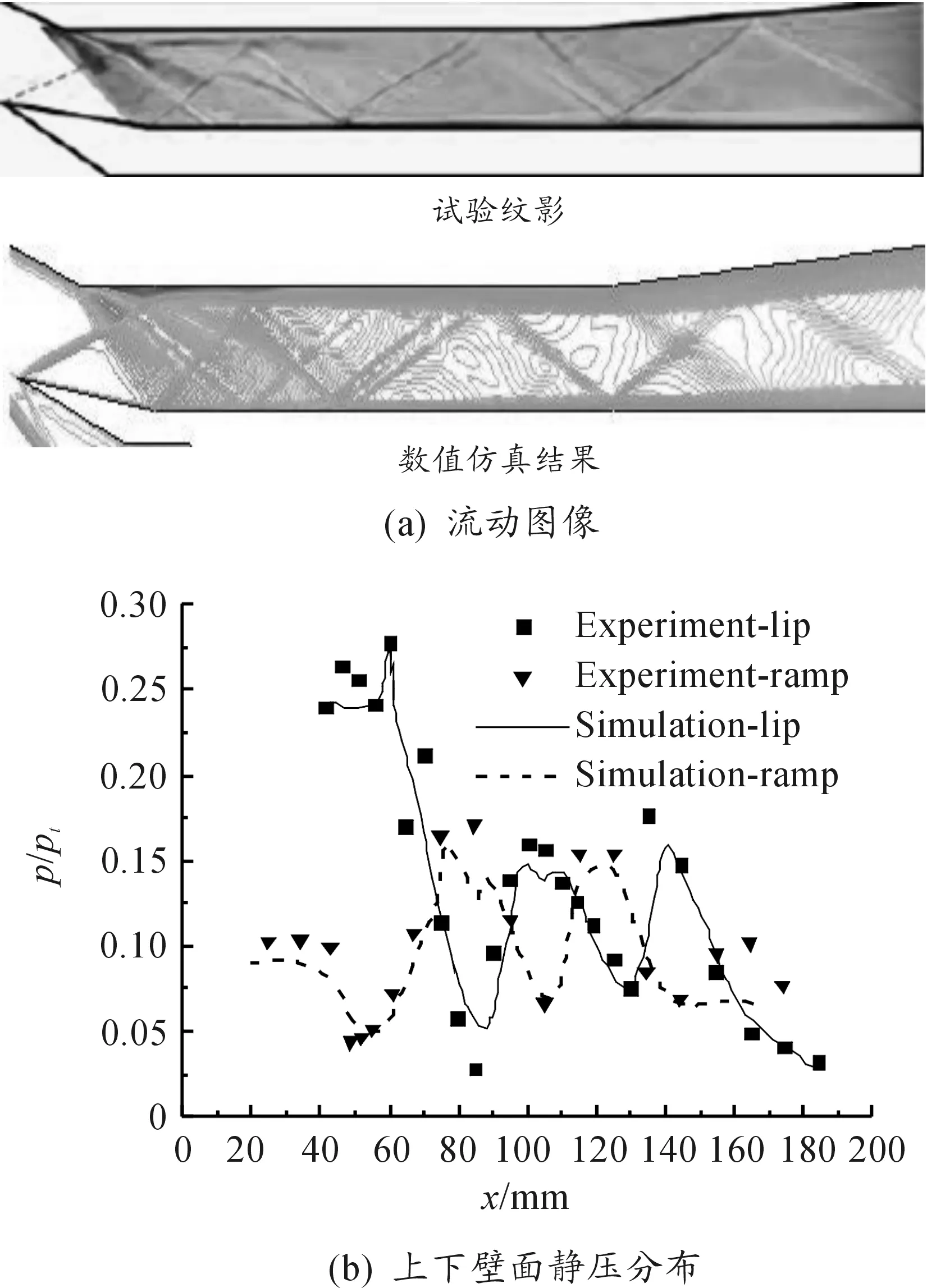
图3 数值仿真结果与试验结果对比

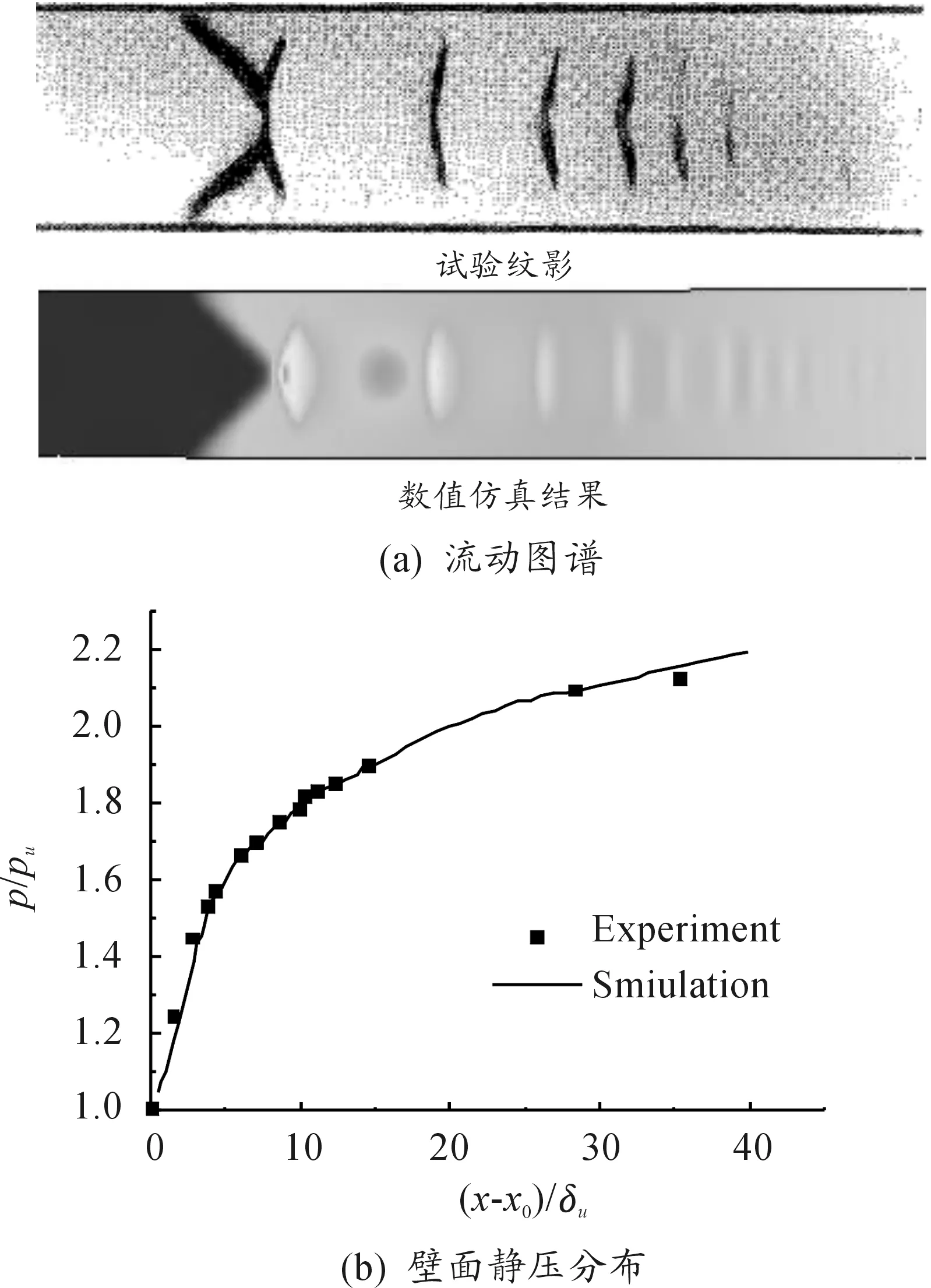
图4 数值仿真结果与试验结果对比

2 计算结果与讨论

2.1 隔离段内激波串迟滞回路现象

图5为均匀入口条件隔离段内激波串起始位置随反压的变化关系。可以看出：升压过程，激波串起点随反压升高逐渐向上游移动，反压较低时激波串起点位置与反压几乎成线性变化关系，反压较高时，相同压升引起激波串起始位置向前移动的距离增大，符合经典Waltrup预测公式。降压过程中，激波串起点随反压的降低逐渐向下游移动，趋势与升压过程正好相反：反压较高时，反压降低引起的激波串起点向下游变化较大，反压较低时，降低同样大小的反压引起激波串起点向下游移动的距离较短。可以看到：不管是升压还是降压过程，只要出口反压相同，激波串均稳定在同一位置。

图5 均匀入口条件隔离段内激波串起始位置随反压的变化

图6为真实入口条件隔离段内激波串起始位置随反压的变化关系。可以看到，与均匀入口条件隔离段不同，在来流条件相同的情况下，反压上升和下降的过程中达到同一反压值时，真实入口条件隔离段内激波串起点却不在同一位置，甚至相差很远，即出现激波串迟滞回路现象。在不同的压力变化过程中，同一反压下隔离段内的激波串可以稳定在两个不同位置，因此说明升压与降压过程对真实入口条件隔离段内的流动特性产生了重要影响。

2.2 激波串迟滞回路对隔离段性能的影响

从图6中可以看出：反压上升时，激波串起始位置逐渐向隔离段入口靠近的过程中出现了激波串起始位置突变现象，即在某个反压值下，若反压继续增加1%就会引起激波串起点突然向上游移动很长距离Δx′，本文把此时的反压称为上临界压力，用pc′表示，对应的激波串起点位置称为上临界位置，用xc′表示；同理，反压降低时，激波串起始位置逐渐向隔离段出口靠近的过程中，若反压再继续减小1%就会引起激波串突然向下游移动很长距离Δx，将此时的反压称为下临界压力，用pc表示，同时下临界压力对应的激波串起点位置称为下临界位置，用xc表示。

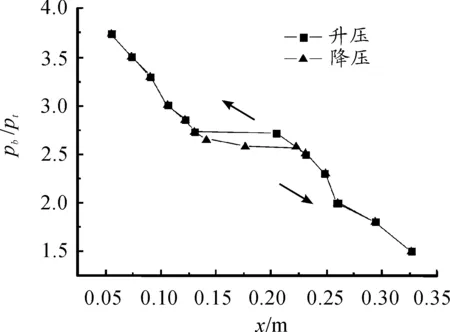
图6 真实入口条件隔离段内激波串起始位置随反压的变化

表2、表3分别为真实入口条件隔离段上下临界参数，可以看到：上下临界压力值之间相差7.3%；同一反压下，升压与降压过程中激波串位置相差约为隔离段高度的1.3倍。此外，上临界压力高于下临界压力(pc′ >pc)，下临界位置比上临界位置更靠近隔离段入口，说明升压过程中，要使激波串前缘从斜激波入射点的下游跨过斜激波到斜激波入射点的上游，比降压时从斜激波上游跨过斜激波到下游时需要更高的反压。

表2 上下临界压力

表3 上下临界位置

图7是真实入口条件隔离段激波串迟滞回路前后的总压恢复系数随反压的变化关系。从图中可明显看出：当施加的反压大于上临界压力或者小于下临界压力时，升压与降压过程中隔离段的总压恢复系数变化是相同的。反压相同则总压恢复系数相同。因此，可以说明在上述反压范围内隔离段内总压恢复系数不受反压变化过程的影响。当施加的反压在上下临界压力区间内时，总压恢复系数随反压变化呈现较大幅度的波动。

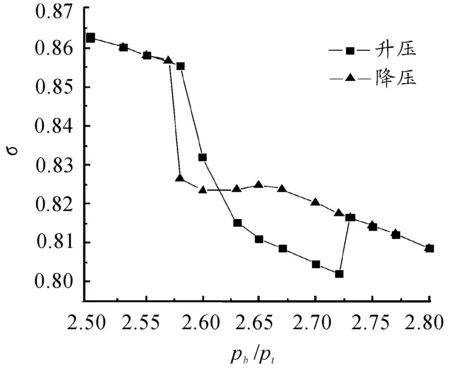
图7 总压恢复系数随反压的变化

图8为升压与降压过程中真实入口条件隔离段出口反压为上临界压力时的流场结构及壁面压力。可以看到：相同反压下，反压升高与降低过程得到的流场结构完全不同，激波串初始激波形态与强度均相差较大；升压过程的激波串长度明显小于降压过程，且激波串对称性比降压过程好；升压过程中隔离段内形成了两道强度较大的波节，中心线压力出现了两次峰值；降压过程中，隔离段内的波节数目增多，中心线压力波峰波谷数量也随之增加，波节之间的间距减小，初始激波强度明显较弱，每道波节强度小于升压过程。

2.3 激波串迟滞回路现象产生的原因分析

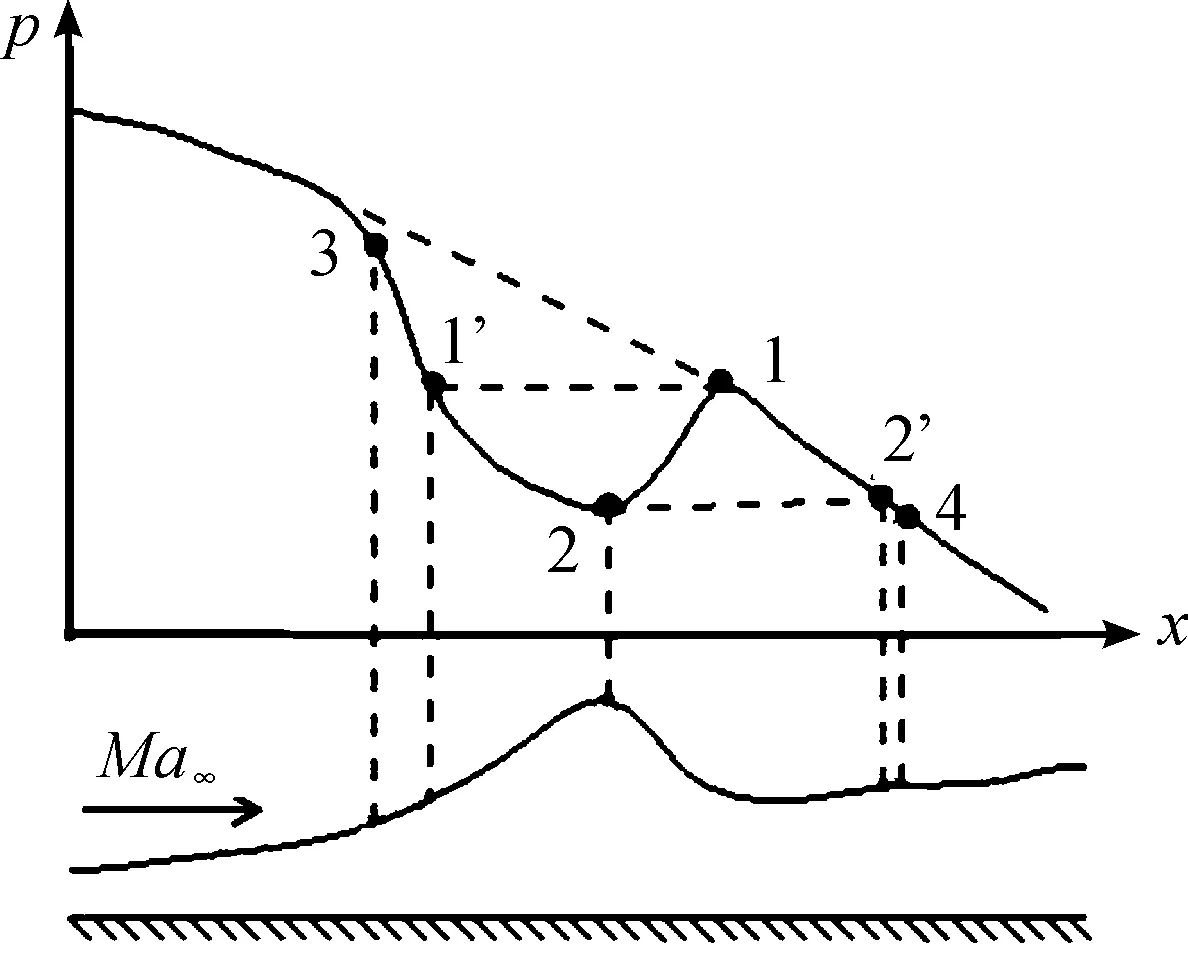
实际工作中，隔离段受到前方进气道产生的斜激波及膨胀波干扰，其内部流动是一系列以激波边界层干扰为主要特征的复杂流动。为了便于研究，现建立真实入口条件隔离段内分离区简化模型及抗反压能力简化曲线，如图9所示。气流流向从左向右，图中横坐标x表示位置(若x1

图8 反压pb/pt=2.89时流场及壁面压力

图9 分离区简化模型及抗反压能力简化曲线

对隔离段施加反压后(反压用pb表示)会产生激波串，反压升高促使激波串向上游发展，正常情况下，如果施加的反压与激波串前缘点(x点)的抗反压能力相当，即pb=px，其中px表示位置x处的抗反压能力，那么激波串就会稳定在x点。如果pb>px，激波串就会被高反压继续推向x点的上游，如果pb

在升压过程中，随着反压的不断增加，激波串逐渐向上游移动，若pb=px2，则激波串稳定在x1位置，且此时的pb值也等于上文中提到的上临界压力值pc′。若继续施加一个小的压力扰动Δp，Δp为正且为趋于0的无穷小量，则pb+Δp>px2，即点1处能承受的反压值小于施加的反压值，因此高的反压将继续推动激波串向上游发展。但是从抗反压曲线可以看出，在x1′和x1之间抗反压能力值均小于pb+Δp，直到到达x1′上游的某个位置时才出现抗反压能力为pb+Δp的点，此时激波串得以稳定，之后随反压的继续增加激波串沿着图中的抗反压能力曲线正常向上游移动，不再出现“跳跃”的现象，除非再次遇到分离区，重复上述过程。

在降压过程中，随着反压不断减小，激波串逐渐向下游移动，在图中的2点位置x2之前，分离区内都存在一个与降低后的反压值相等的抗反压能力点，因此反压在未降到下临界反压pc前，不会出现激波串“跳跃”现象。当激波串到达x2位置时，即反压值pb与下临界反压值pc相等，此时若pb=px2，激波串则可以在x2位置处稳定，但若有一个小的压力扰动-Δp，-Δp小于0且无限趋近于0，则pb-Δp

3 结论

1) 均匀入口条件下升压与降压过程对隔离段内的流动特性基本不产生影响，而真实入口条件下升压和降压过程中隔离段内则出现了激波串迟滞回路现象。

2) 真实入口条件下反压上升过程中存在上临界压力pc′，使得出口反压稍大于上临界压力时，隔离段内激波串会向上游突增Δx′；反压下降过程中存在下临界压力pc，使得反压稍小于下临界压力时，激波串会向下游突减Δx，且上临界压力大于下临界压力。

3) 在上下临界压力区间内，升压与降压过程中同一反压下隔离段内激波串位置相差约为隔离段高度的1.3倍，且激波串形态、壁面压升规律、总压恢复系数均差异明显。

4) 利用隔离段内分离区前后的流动简化模型以及抗反压能力简化曲线，分析得出激波串迟滞现象主要是由激波边界层干扰诱导的分离造成的。真实情况下，分离区内的流动现象要比简化模型更加复杂。