贝塞尔曲线在浮式风力机模型试验中的应用

陈鸣芳，陈哲，何炎平，孟龙

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心（船海协创中心），上海 200240；3.上海交通大学船舶海洋与建筑工程学院，上海 200240）

近年来，风电行业得到进一步发展。如2016年，国家发展改革委发布的《可再生能源发展“十三五”规划》明确指出，要全面协调推进风电开发，到2020年底，风电并网装机确保达到2.1亿千瓦以上。海上风电由于来流稳定、速度大，已逐渐成为重点发展方向。为更好的利用海上风电资源，国内科研院所积极开展不同形式的浮式风力机模型试验。如上海交通大学海洋工程水池开展的TLP型浮式风力机模型试验，哈尔滨工程大学海洋可再生能源实验室开展的Spar型浮式风力机模型试验等。在浮式风力机模型试验中，由于满足弗汝德相似定律，试验产生较为严重的尺度效应，导致几何相似叶片产生的推力远小于目标推力。为保证试验的准确性，美国缅因大学Martin等在试验中尝试对比多种消除尺度效应的方法，提出重新设计模型叶片的方法可以较好的满足试验要求。

本文以某6MW海上浮式风力机模型试验为例，在弗汝德相似条件下，确定模型缩尺比为1：65.3。文章采用三次贝塞尔曲线定义模型叶片弦长和扭角沿展向分布，通过模式搜索法优化曲线控制点坐标得到满足推力相似的模型叶片，并对多种试验工况进行分析。

1 设计理论

1.1 叶素-动量理论

本文采用叶素-动量理论计算模型叶片推力。其基本思路是将叶片分为若干个有限微段，分别对每个微段进行受力分析，最终确定整个叶片受力情况。对于单个微段，当忽略相邻叶素干扰时，可将其看作二维翼型，其受力情况如图1所示。

根据动量方程和叶素方程，通过迭代法确定每段叶素轴向和周向诱导因子，进而求得叶素所处雷诺数大小。根据雷诺数和攻角数值，得到翼型升、阻力系数，确定叶素推力数值。最后，将所有叶素受到的风轮推力叠加得到模型叶片推力。由于在模型叶片优化设计中，叶素所处雷诺数和攻角数值随着优化过程不断变化，为简便计算，叶素升阻力系数建议采用低雷诺数升阻力系数图谱确定。

图1 叶素受力分析图

1.2 贝塞尔曲线

贝塞尔曲线是法国工程师贝塞尔在1962年提出的，其形状由曲线控制点确定，通过改变控制点位置可以实现曲线形状的变化。其中，控制点起、终点与曲线的起、终点重合。

为保证模型叶片弦长和扭角沿展向连续分布，本文采用三次贝塞尔曲线定义弦长和扭角沿展向变化。三次贝塞尔曲线的参数公式为：

2 设计方法

2.1 叶片参数化表示

在模型叶片优化设计中，首先需要确定优化变量。试验任务书提供的原型叶片为离散数据，不利于叶片优化设计，需要对叶片进行参数化表达，以确定优化变量。上海交通大学杜炜康等通过四次曲线和二次曲线分别表示叶片弦长和扭角沿展向变化。本文采用三次贝塞尔曲线定义模型叶片弦长和扭角沿展向分布，即在叶片展向位置分别定义4个控制点。其中，初始点为叶根处，终点为叶尖处，中间控制点分别布置在叶片距叶根37%和72%处，如图2所示。

图2 三次贝塞尔曲线定义几何相似叶片弦长和扭角

2.2 叶片优化设计

在叶片优化设计中，保持曲线控制点沿展向位置不变，只改变控制点纵向坐标实现曲线形状的变化。其中，弦长和扭角曲线的起点和终点固定不动，则优化变量共有4个，即四点纵向坐标值。以额定试验工况下目标推力值为优化设计目标，通过模矢搜索法对4个变量进行优化，最终得到满足目标推力值的模型叶片，如图3所示。

由图3可知，优化后，模型叶片弦长曲线控制点纵向坐标增加，为弦长增大，且增大区域主要集中在叶片中部；扭角曲线控制点纵向坐标减小，为扭角减小，减小区域主要集中在叶尖处。

3 对比分析

为更好的研究浮式风力机性能，在模型试验中，需要对风力机转子在多种不同工况下进行试验分析。本文根据模型试验任务书选取7种工况，对第2部分设计的模型叶片进行计算分析，并与上海交通大学杜炜康等设计的模型叶片进行对比，如图4所示。

由图可知，在额定工况下，贝塞尔曲线拟合法和多项式曲线拟合法均可得到满足试验目标推力值的模型叶片。在其他工况下，贝塞尔曲线拟合法得到的模型叶片明显优于多项式曲线拟合法得到的叶片。

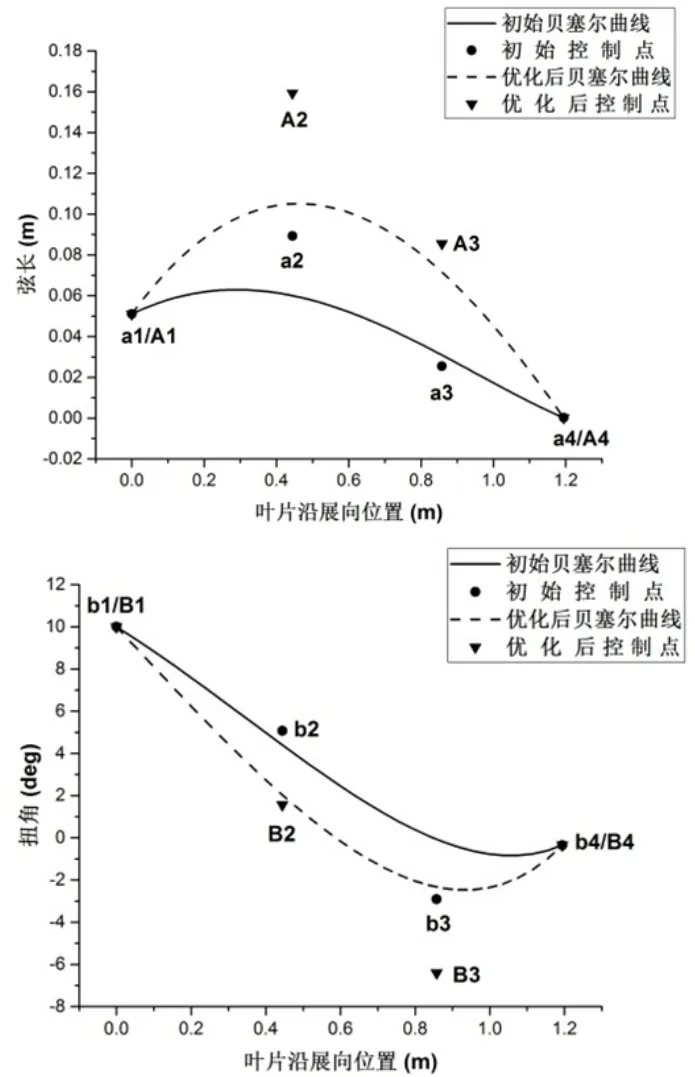
图3 叶片弦长和扭角优化前后对比

图4 不同叶片推力数值对比

4 结语

（1）利用三次贝塞尔曲线定义模型叶片弦长和扭角沿展向分布情况，以额定工况下目标推力值为优化设计目标，采用模式搜索法对模型叶片进行优化设计，得到满足试验要求的模型叶片。

（2）与多项式曲线拟合得到的叶片对比分析，贝塞尔曲线拟合得到的叶片在其他试验工况下表现良好，具有较好的适应性。