基于流体动力学的膏体料浆动水压力研究

张爱卿，吴爱祥，王贻明，王洪江，尹升华，王正英

基于流体动力学的膏体料浆动水压力研究

张爱卿1，吴爱祥1，王贻明1，王洪江1，尹升华1，王正英2

(1. 北京科技大学 土木与资源工程学院，北京，100083； 2.临沂会宝岭铁矿有限公司，山东 临沂，277712)

基于流体动力学，借鉴泥石流冲击力的研究成果，建立膏体料浆动水压力力学模型，以某膏体充填矿房为工程实例，开展膏体料浆对充填挡墙作用力的现场监测试验，分析膏体料浆动水压力的变化规律。研究结果表明：假定膏体料浆可稳定流动，当膏体料浆的密度和浓度一定时，塑性黏度不变，膏体料浆的平均流速与阻力坡降和膏体料浆高度的幂呈正相关，膏体料浆动水压力与阻力坡降的幂和膏体料浆高度的4次幂呈正相关；固结作用对膏体料浆动水压力有较大的影响，现场试验三期充填过程中，二期充填时膏体料浆动水压力对充填挡墙作用十分显著，距充填挡墙底部2/3处最大动水压力超过最大静水压力。

动水压力；膏体料浆；力学模型；动力学；充填挡墙

膏体充填技术经过多年探索与实践，其因具有环保、节能、减排、安全、高效等优点已在全世界被广泛认可并应用[1−4]，大量工程实践表明膏体料浆在充填入矿房时会对充填挡墙产生一定的冲击作用，为了保证矿山充填安全，膏体料浆作用于充填挡墙上冲击力已引起国内外专家学者的重视，但与此相关的研究尚未见报道，因此，亟需对膏体料浆作用于充填挡墙的冲击力开展研究。近年来，国内外研究者对作用于充填挡墙作用力进行了研究，将充填过程中充填挡墙承受充填料浆的作用分为静水压力、动水压力和固化膨胀力。大部分研究主要是将胶结充填体当成理想液体，考虑到料浆的低流速，忽略胶结充填体动水压力对充填挡墙的影响，只考虑静止状态的理想填料作用于挡墙的荷载，并基于土力学中土压力理论建立作用充填挡墙的力学公式[5−17]。吴已成等[18]通过分析新型固化剂胶结尾砂充填过程，得出充填挡墙主要受到充填料浆对充填挡墙的静压力及充填体自身固化凝结产生的膨胀力的作用，充填料浆自身的膨胀力对充填挡墙的稳定性影响较小，可以忽略。杜雪鹏[19]针对块石充填料运动机理展开了研究，假设块石充填颗粒为刚性球体，从碰撞力学角度建立了采场内块石运动机理模型。张葆春等[20]对通过现场充填挡墙压力监测试验，得出前期充填料浆对压力盒反复的冲击是监测值发生波动的主要原因，且充填挡墙上部压力盒受充填料浆动水压力作用影响显著，表明充填料浆对充填挡墙的动水压力是不能忽视的，但并未给出动水压力计算公式。本文作者基于流体动力学对膏体料浆动水压力展开研究，借鉴泥石流冲击力的研究成果，建立膏体料浆动水压力力学模型表达式，分析膏体料浆动水压力的变化规律，以某矿膏体充填矿房为工程实例，开展现场监测试验，分析充填过程中不同充填阶段膏体料浆动水压力的变化规律，并验证膏体料浆动水压力公式的正确性，研究成果可用于指导充填挡墙设计，保证矿山充填的安全，具有一定的工程实用意义。

1 基于流体动力学的膏体料浆动力压力理论分析

总结多年膏体充填工程经验可知，膏体料浆对充填挡墙产生的动水压力与泥石流分类中泥流的冲击力较为相近：1) 都是以细颗粒组成为主；2) 以悬移形式输移运动，其中细颗粒与水体一起构成了相对稳定的浆体，与水流同步运动；3) 流动过程中颗粒之间都会产生相互作用，且产生的冲击力都随时间而变化。因此，膏体料浆在矿房中的运动可以简化为图1所示模型。图1中：为流速；为料浆高度；为高度；B为非流核区高度；为坡度；B为宾汉极限剪应力；0为最大剪应力。

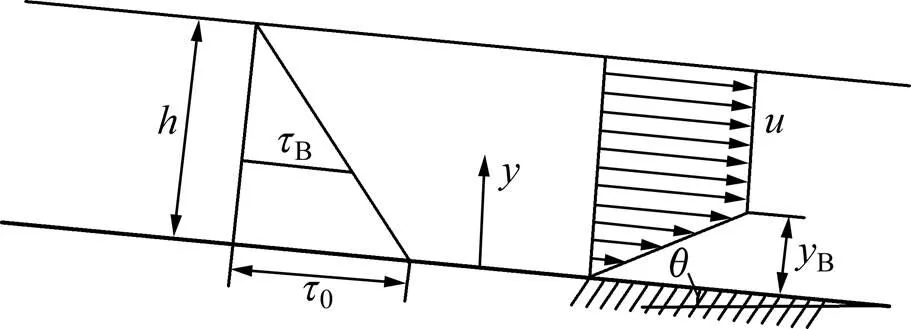
图1 膏体料浆在矿房中的运动模型

对于完全由细颗粒组成的浆体，即使处在静止状态，其垂向的浓度分布也十分均匀[21]。流变试验结果表明：膏体料浆在一定浓度下属于宾汉体，膏体料浆在二维流动中离床面任一高程处的剪应力为

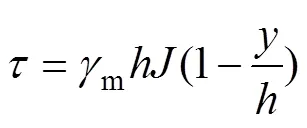
式中：为剪应力，kPa；为阻力坡降；m为膏体料浆的容重，N/m3。

在层流流态时，流速分布存在流核区。当≤B时，由于水流剪应力小于泥流的宾汉剪应力，因而流层间无相对运动，在≥B处各层流速相等，即所谓流核区。在=B处，=B，由式(1)有

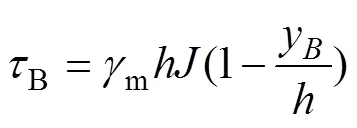
由式(2)得非流核区的厚度B为

在非流核区，由于＞B和＜B，存在流速梯度，由宾汉模型及式(1)，可得

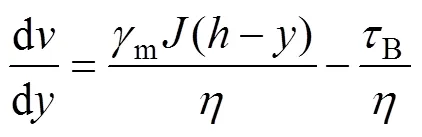
式中：为塑性黏度，Pa∙s。

对式(4)积分，便得非流核区的流速分布公式：

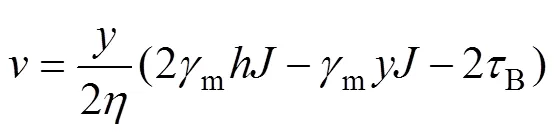
将式(3)代入式(5)，得≥B，流核区的流速p为

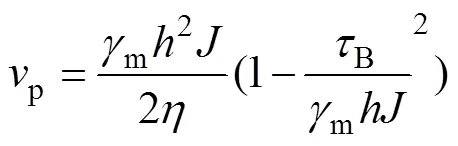
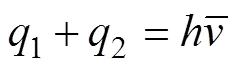
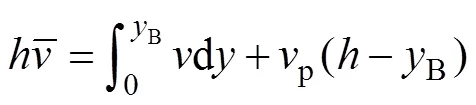
将式(8)积分整理后便得层流状态下膏体料浆的平均流速公式：

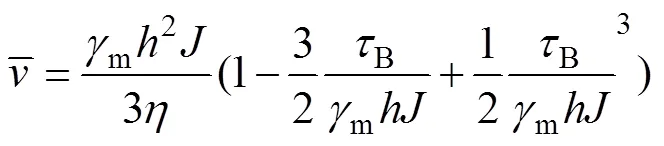
采用宾汉体模型计算流速的局限性在于只适用于层流流态。式(9)所示流速公式是按层流流态导出的，大量试验及实测结果均表明，在紊流流态下，宾汉剪应力B往往明显减少，甚至完全消失[21]。

因此，考虑膏体料浆在矿房内部流动的复杂情况，在紊流状态下平均流速式(9)可简化为

邓检良等[22]通过自主研发的旋转水槽制作稳定循环流动的泥石流，发现泥石流的阻力坡降等于槽底坡降tan。假设膏体料浆在矿房中的流动也满足稳定流动要求，则式(10)可转化为

式中：为充填矿房槽底坡度，(°)。

从式(11)可以看出：当膏体料浆的容重一定时，若膏体料浆的浓度不变，则塑性黏度不变，膏体料浆的平均流速与槽底坡降tan和膏体料浆高度的幂呈正相关。

基于流体动力学理论[23]，借鉴国内外有关泥流最大冲击力的研究成果[21, 24]，建立膏体料浆动水压力力学模型，其表达式为

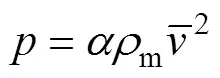
将式(11)代入式(12)，可得膏体料浆动水压力公式为

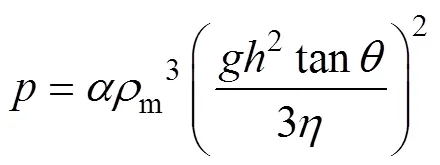
从式(13)可知：膏体料浆的动水压力与膏体料浆的密度、浓度、塑性黏度、槽底坡降和膏体料浆高度相关。当膏体料浆的密度和浓度一定时，塑性黏度不变，膏体料浆动水压力与槽底坡降tan和膏体料浆高度有关，则式(13)可简化为

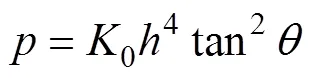
2 工程实例

本文以某金属矿膏体充填矿房为例，分析膏体料浆高度和槽底坡降对膏体料浆动水压力的影响规律；考虑充填过程中不同充填阶段对膏体料浆动水压力的影响，开展现场监测试验分析膏体料浆动水压力的变化规律，并与理论公式计算结果比对，为定量分析膏体料浆动水压力提供参考。

2.1 膏体料浆动水压力变化规律分析

膏体料浆的灰砂比为1:8，其中全尾砂的密度为1.825 g/cm3，膏体料浆的密度为1.413 g/cm3。根据膏体料浆流变理论的研究可知，膏体料浆的塑性黏度与浓度之间有着密切的关系[1−4]，因此，通过室内流变试验测定膏体料浆在质量分数为78%时塑性黏度为0.118 Pa∙s。根据工程经验选择膏体料浆充填高度为1.5 m，假定槽底坡度分别为1.0°，1.5°，2.0°，2.5°，3.0°，3.5°和4.0° 7个水平划分，先求出槽底坡降，再进行膏体料浆动水压力求解，计算结果如图2所示。

图2 膏体料浆动水压力随槽底坡降的变化图

从图2可知：膏体料浆动水压力随着槽底坡降的增加而不断增大，且呈幂次关系。这表明槽底坡降越大，膏体料浆动水压力对充填挡墙的作用就越大，因此，在工程中应严格控制槽底坡降。

其他参数不变，当槽底坡度为1.0°时，槽底坡降为0.02，膏体料浆高度分别为1.0，1.5，2.0，2.5，3.0，3.5和4.0 m 7个水平划分，进行膏体料浆动水压力求解，计算结果如图3所示。

图3 膏体料浆动水压力随膏体料浆高度的变化图

从图3可知：膏体料浆动水压力随着膏体料浆高度的增加而不断增大，且呈4次幂关系。表明膏体料浆充填高度越大，膏体料浆动水压力对充填挡墙的作用就越大。

从理论公式的角度分析，膏体料浆动水压力与槽底坡降和膏体料浆高度有关，在实际工程中，膏体料浆不能1次连续充填至充填挡墙顶部，因此，除了这2个影响因素外，在充填过程中，不同充填阶段的膏体料浆动水压力对充填挡墙产生影响也不尽相同。下面将通过现场监测试验，针对充填过程中不同充填阶段膏体料浆动水压力的变化规律展开研究。

2.2 不同充填阶段膏体料浆动水压力分析

为了分析充填过程中不同充填阶段膏体料浆动水压力的变化规律，选取膏体充填矿房开展现场监测试验，在充填挡墙上安装VWE−2.5型振弦式土压力计，用于监测膏体料浆充填过程中对充填挡墙产生的作用力。充填挡墙长度为4 m，高度为3.7 m，厚度为0.5 m，充填挡墙为钢筋混凝土挡墙，强度为C30，钢筋为直径20 mm的螺纹钢，钢筋间距为300 mm。在充填挡墙的受力分析[12−14]和参考已有工程案例[15−17]的基础上，对试验矿房的充填挡墙布设监测点，第1排监测仪器距离挡墙底部平均为0.50 m；第2排监测仪器距离挡墙底部1/3处，平均为1.23 m；第3排监测仪器距离挡墙底部2/3处，平均为2.40 m。将监测仪器进行编号，例如D1-1为第1排第1个监测点，其他监测点依次编号，如图4所示。试验矿房分三期充填，具体充填工况如表1所示。膏体充填矿房三期充填结束后，随着水泥不断水化，膏体料浆不断硬化，对充填挡墙产生的作用逐渐降低，因此，本文仅分析膏体料浆硬化之前的监测应力，监测结果如图5~7所示。

图4 现场监测仪器布置图

表1 充填工况

1—D1-1；2—D1-2；3—D1-3。

从图5可以看出：一期充填阶段开始后第1排监测曲线有一定程度的波动，表明膏体料浆对充填挡墙产生了动水压力作用；随着充填高度的增加，应力监测值基本呈线性增长，表明膏体料浆对充填挡墙产生的动水压力作用是短暂的，后期充填挡墙主要承受膏体料浆静水压力的作用；在二期充填阶段，监测曲线中出现了显著波动，表明此膏体料浆对充填挡墙产生了较大的动水压力作用；在三期充填阶段，监测数据的变化不大，表明此时膏体料浆动水压力对充填挡墙底部的作用小，膏体料浆静水压力起主要作用。

从图6和图7可知：随着膏体料浆充填高度不断增大，第2排和第3排的监测曲线逐渐呈现相似的变化规律，即在二期充填阶段时两排监测曲线均出现了显著波动，表明膏体料浆对充填挡墙产生的动水压力十分显著。如图5所示，二期充填阶段时膏体料浆产生的最大动水压力超过了最大静水压力。在三期充填阶段，第2排和第3排监测曲线出现了一定程度的波动，表明膏体料浆对充填挡墙中部及上部有一定的动水压力作用，但对充填挡墙作用不大，充填挡墙主要以承受膏体料浆的静水压力作用为主。

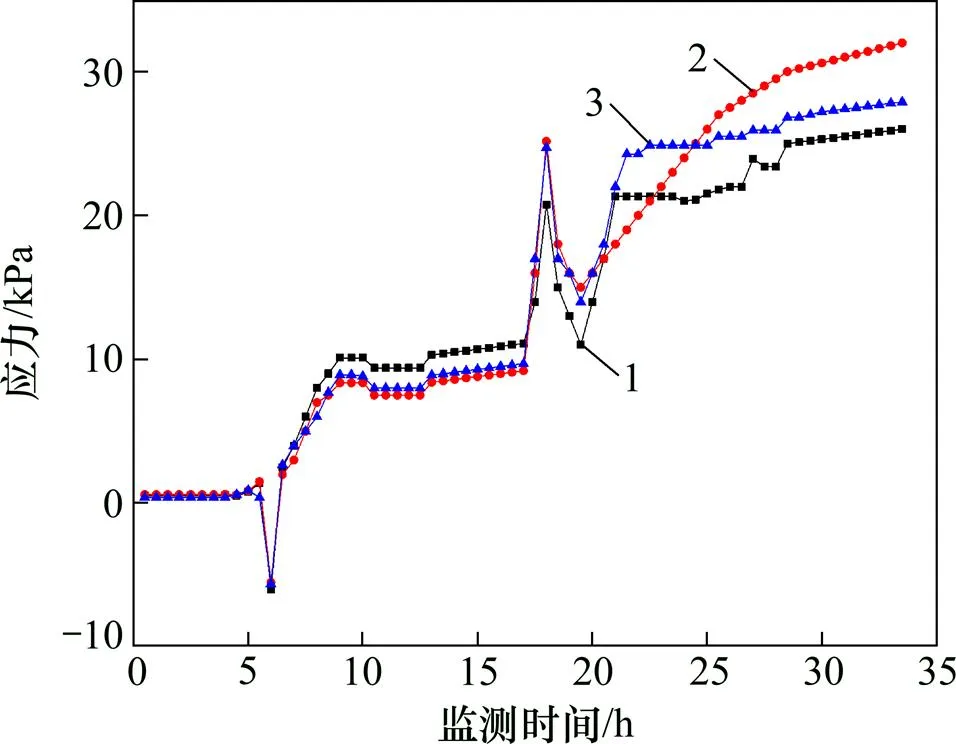
1—D2-1；2—D2-2；3—D2-3。

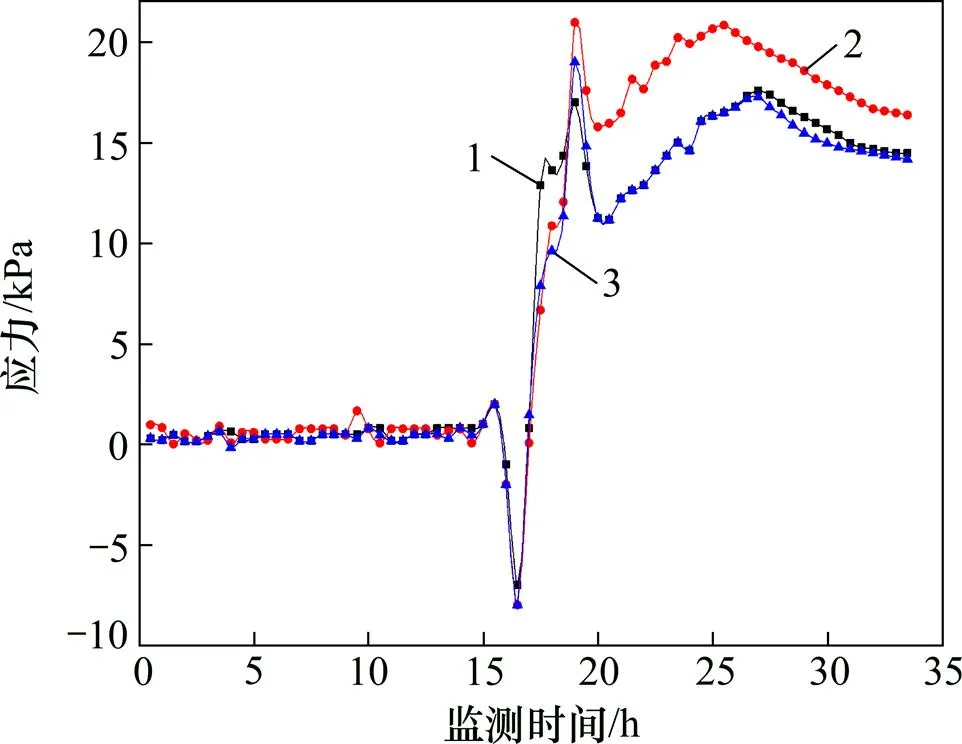
1—D3-1；2—D3-2；3—D3-3。

综上可知，膏体料浆动水压力在充填过程中的变化规律为：在一期充填阶段，膏体料浆动水压力相比静水压力对充填挡墙的作用很小，甚至可以忽略；比二期充填阶段，膏体料浆动水压力对充填挡墙的作用较大，距离充填挡墙底部2/3处出现了最大动水压力超过了最大静水压力的现象；在三期充填阶段，膏体料浆动水压力对充填挡墙的作用较小。因此，在分析充填挡墙承受作用力时，应重视二期充填阶段膏体料浆对充填挡墙产生的动水压力。

2.3 现场试验结果与理论公式计算结果比对

根据工程经验选择膏体料浆充填高度分别为0.5，1.0，1.5，2.0和2.5 m共5个水平划分，将对应膏体料浆充填高度的监测点结果求平均值得到现场试验监测结果。现场实测充填矿房槽底坡度约为1.0°，则阻力坡降为0.02，其他参数不变，代入式(14)求解膏体料浆动水压力，与现场监测试验结果进行比对，如图8所示。

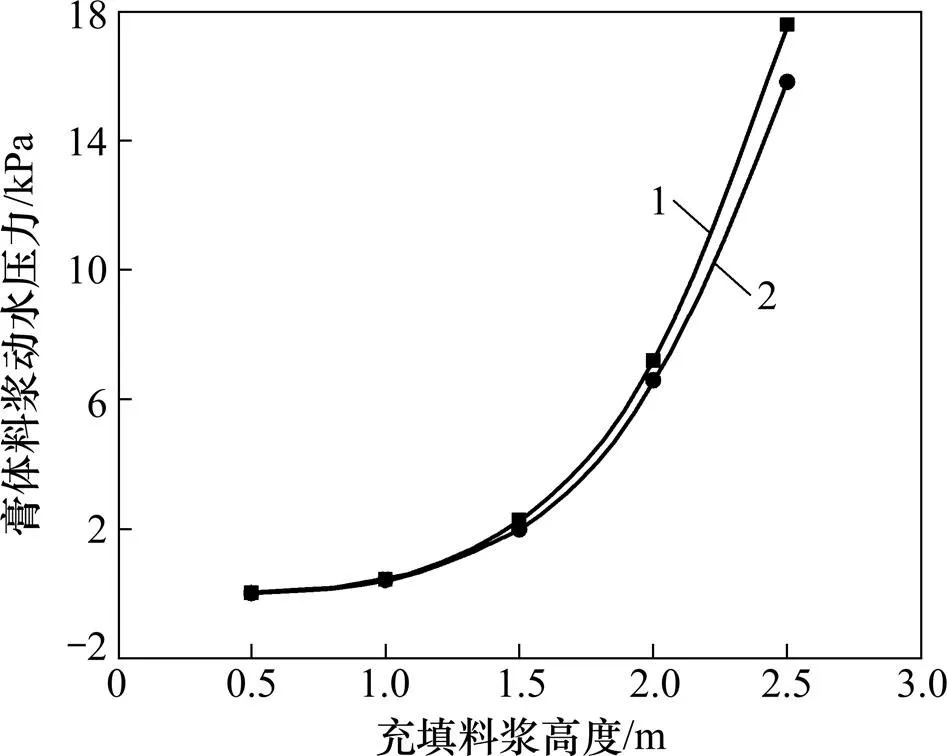
1—理论公式计算结果；2—现场试验监测结果。

从图8可知：不论是理论公式计算结果还是现场试验监测结果，膏体料浆动水压力随着膏体料浆高度的增大而增大。理论公式计算结果曲线与现场试验监测结果曲线相近，在膏体料浆充填高度小于1.5 m时，两者曲线基本吻合，由于现场试验过程中膏体料浆有一定的固结时间，当膏体料浆充填高度大于1.5 m时，现场试验监测结果均小于理论公式计算值。

本文推导得出的理论公式是建立在膏体料浆为稳定流动的前提下，而在实际工程中，膏体料浆在充填矿房中的运动受到多方面因素的影响不会呈稳定流动，且未考虑充填阶段固结作用对膏体料浆动水压力的影响，因此，导致理论公式计算结果偏大，但以理论计算结果作为充填挡墙的设计依据，可以保证充填挡墙的安全。在实际工程中，室内试验测定膏体料浆的密度、浓度和塑性粘度，现场实测槽底坡度计算阻力坡降，就可以利用本文推导得出的理论公式计算不同充填阶段时的膏体料浆动水压力，具有一定工程实用意义。

3 结论

1) 基于流体动力学，在借鉴泥石流冲击力研究成果的基础上，建立了膏体料浆动水压力力学模型，假设膏体料浆可稳定流动，当膏体料浆的密度和浓度一定时，塑性黏度不变，膏体料浆动水压力与槽底坡降的幂和膏体料浆高度的4次幂均呈正相关。

2) 据现场监测试验分析得出充填过程中膏体料浆动水压力的变化规律：在一期充填阶段，膏体料浆动水压力相比静水压力对充填挡墙的作用很小，甚至可以忽略；在二期充填阶段，膏体料浆动水压力对充填挡墙的作用较大，距离充填挡墙底部2/3处出现了最大动水压力超过了最大静水压力的现象；在三期充填阶段，膏体料浆动水压力对充填挡墙的作用较小。在分析充填挡墙承受作用力时，应重视二期充填阶段膏体料浆对充填挡墙产生的动水压力。

3) 膏体料浆动水压力理论公式计算曲线与现场监测曲线相近，且理论公式计算结果均大于现场实测值，验证了理论公式的正确性和合理性。在实际工程中，室内试验测定膏体料浆的密度、浓度和塑性黏度，现场实测槽底坡度计算阻力坡降，就可以利用本文推导得出的理论公式计算出膏体料浆动水压力，具有一定工程实用意义。

[1] WU Aixiang, WANG Yiming, WANG Hongjiang, et al. Coupled effects of cement type and water quality on the properties of cemented paste backfill[J]. International Journal of Mineral Processing, 2015, 143: 65−71.

[2] WU Aixiang, WANG Yiming, WANG Hongjiang. Estimation model for yield stress of fresh unceented thickened tailings: coupled effects of true solid density, bulk density, and solid concentration[J]. International Journal of Mineral Processing, 2015, 143: 117−124.

[3] 吴爱祥, 王洪江. 金属矿膏体充填理论与技术[M]. 北京: 科学出版社, 2015: 1−5. WU Aixiang, WANG Hongjiang. Paste backfill theory and technology of metal mine[M]. Beijing: Science Press, 2015: 1−5.

[4] 王新民, 古德生, 张钦礼. 深井矿山充填理论与管道输送技术[M]. 长沙: 中南大学出版社, 2010: 1−12.WANG Xinmin, GU Desheng, ZHANG Qinli. Theory of backfilling activity and pipeline transportation technology of backfill in deep mines[M]. Changsha: Central South University Press, 2010: 1−12.

[5] 黄建君. 充填法挡墙强度模型研究及应用[D]. 昆明: 昆明理工大学国土资源工程学院, 2014: 21−28. HUANG Jianjun. Research and application of filling method of retaining wall strength mode[D]. Kunming: Kunming University of Science and Technology. College of L and and Resources, 2014: 21−28.

[6] 张海波, 刘芳芳. 充填采矿法充填挡墙合理结构参数研究及应用[J]. 化工矿物与加工, 2014, 43(5): 33−35. ZHANG Haibo, LIU Fangfang. Research and application of reasonable structural parameters for filling retaining wall in cut-and-fill mining method[J]. Mineral and Chemical Processing, 2014, 43(5): 33−35.

[7] 费东, 邓代强, 姚中亮. 哈图金矿采空区充填挡墙封堵实践[J]. 矿业研究与开发, 2013, 33(2): 28−29, 92. FEI Dong, DENG Daiqiang, YAO Zhongliang. Practice of bulkhead construction for the filling of mined-out area in Hatu gold mine[J]. Mining R&D, 2013, 33(2): 28−29, 92.

[8] ZHOU Baojing, XU Jinhai, ZHAO Maosen, et al. Stability study on naturally filling body in gob-side entry retaining[J]. International Journal of Mining Science and Technology, 2012, 22(3): 423−427.

[9] TAN Yunliang, YU Fenghai, NING Jianguo, et al. Design and construction of entry retaining wall along a gob side under hard roof stratum[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 77: 115−121.

[10] YU Guangyun, BAI Yongsheng, SHENG Ping, et al. Mechanical performance of a double-face reinforced retaining wall in an area disturbed by mining[J]. Mining Science and Technology, 2009(19): 36−39.

[11] HELINSKI M, FAHEY M, FOURIE A. Behavior of cemented paste backfill in two mine stopes: measurements and modeling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(2): 171−182.

[12] STREUDERS S B. Rock engineering related experiences with the use of backfill on the deepest platinum mine[C]//Minefill 2011, 10th International Symposium on Mining with Backfill. Cape Town, Southern African: Euler De Souza Publications, 2011: 49−64.

[13] NORTJÉ A S, MEINTJIES H A C, JOUGHIN W C. Design of hydraulic backfill bulkheads at south deep gold mine[R]. Montreal: Minefill, 2007: 1−11.

[14] KANOWNA B, OPERATION R. Assessment of 12 hour fibrecrete curing on raleigh paste bulkheads[R]. Victoria:Revell Resources Pty Ltd, 2010: 1−13.

[15] 王丽红, 李夕兵, 赵国彦, 等. 永平铜矿充填挡墙安全设计及工程应用[J]. 矿冶工程, 2013, 12(6): 6−12. WANG Lihong, LI Xibing, ZHAO Guoyan, et al. Safety design of backfilled retaining wall and its application in Yongping copper mine[J]. Mining and Metallurgical Engineering, 2013, 12(6): 6−12.

[16] 汪海萍, 宋卫东, 张兴才, 等. 大冶铁矿浅孔留矿嗣后胶结充填挡墙设计[J]. 有色金属, 2014, 9(5): 14−26. WANG Haiping, SONG Weidong, ZHANG Xingcai, et al. Design for retaining wall of short-hole shrinkage subsequent cemented filling method in Daye Iron Mine[J]. Nonferrous Metals, 2014, 9(5): 14−26.

[17] 袁世伦. 盘区大孔采矿采场全尾砂充填挡墙力学特性研究[J]. 中国矿山工程, 2011, 8(4): 9−12. YUAN Shilun. Study on mechanical property of whole tailing filling retaining wall in panel large hole mining stope[J]. China Mine Engineering, 2011, 8(4): 9−12.

[18] 吴已成, 谢涛, 罗涛. 新型固化剂胶结尾砂充填挡墙的工程应用[J]. 现代矿业, 2015, 31(12): 206−207. WU Yicheng, XIE Tao, LUO Tao. New type curing agent of cemented backfilling filling retaining wall engineering application[J]. Modern Mining, 2015, 31(12): 206−207.

[19] 杜雪鹏. 采场内块石充填料运动机理研究[D]. 长沙: 中南大学资源与安全工程学院, 2012: 29−31. DU Xuepeng. Research on the movement mechanism of rock filling in stops[D]. Changsha: Central South University. School of Resources and Safely Engineering, 2012: 29−31.

[20] 张葆春, 曹宗权, 赵永和, 等. 尾砂胶结充填挡墙受力分析及工程应用[J]. 有色金属科学与工程, 2011, 2(5): 57−60. ZHANG Baochun, CAO Zongquan, ZHAO Yonghe, et al. Bulkhead stress analysis in filling cemented tailings and its practical application[J]. Nonferrous Metals Science and Engineering, 2011, 2(5): 57−60.

[21] 费祥俊. 泥石流运动机理及灾害防治[M]. 北京: 清华大学出版社, 2004: 114−129. FEI Xiangjun. The mechanism of the flow and the prevention and control of the landslide[M]. Beijing: Tsinghua University Press, 2004: 114−129.

[22] 邓检良, 余斌, 沈水龙. 基于旋转水槽试验的泥石流阻力坡降速率效应研究[J]. 工程地质学报, 2016, 24(5): 976−980. DENG Jianliang, YU Bin, SHEN Shuilong. Effects of flow rate on friction slope of debris flow with rotating flume tests[J]. Journal of Engineering Geology, 2016, 24(5): 976−980.

[23] 刘鹤年. 流体力学[M]. 北京: 中国建筑工业出版社, 2001: 36−44. LIU Henian. Fluid mechanics[M]. Beijing: China Architecture & Building Press, 2001: 36−44.

[24] 费祥俊, 朱程清. 高含沙水流运动中的宾汉切应力[J]. 泥沙研究, 1991(4): 13−23. FEI Xiangjun, ZHU Chengqing. The Bingham stress in the sandwater movement[J]. Sediment Research, 1991(4): 13−23.

[25] 唐金波, 胡凯衡, 周公旦, 等. 基于小波分析的泥石流冲击力信号处理[J]. 四川大学学报(工程科学版), 2013, 45(1): 8−13. TANG Jinbo, HU Kaiheng, ZHOU Gongdan, et al. Debris flow impact pressure signal processing by the wavelet analysis[J]. Journal of Sichuan University(Engineering Science Edition), 2013, 45(1): 8−13.

(编辑 杨幼平)

Study on hydrodynamic pressure of paste slurry based on fluid dynamics

ZHANG Aiqing1, WU Aixiang1, WANG Yiming1, WANG Hongjiang1, YIN Shenghua1, WANG Zhengying2

(1. School of civil and resource engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. Linyi Huibaoling Iron Ore Co., Ltd., Linyi 277712, China)

Based on fluid dynamics and the research achievements of debris flow impact, paste slurry formula of hydrodynamic pressure was established. Using a room of paste filling mining as an engineering example, the monitoring test of the paste of filling slurry retaining wall force field was conducted, and the hydrodynamic pressure change rule was analyzed and the correctness of the theoretical formula was verified. The results show that with the assumption that paste slurry can steadily flow, when the density and the concentration of the paste slurry are certain, plastic viscosity is constant, and the average flow velocity and resistance of paste slurry grade and paste slurry high power are positively correlated, paste slurry hydrodynamic pressure and resistance grade power and four times the height of power of paste slurry are positively correlated. Consolidation effect has a great influence on the hydrodynamic pressure of the paste slurry, field test three times in the filling process, the secondary when filling paste slurry hydrodynamic pressure on retaining wall filling effect is very significant, is apart from the pack at the bottom of the retaining wall, the maximum dynamic water pressure value more than 2/3 of the maximum hydrostatic pressure, verify the correctness and rationality of theoretical formula.

hydrodynamic pressure; paste slurry;mechanical model; dynamics; filling retaining wall

10.11817/j.issn.1672−7207.2018.10.024

TD853

A

1672−7207(2018)10−2561−07

2017−10−10；

2017−12−18

国家重点研发计划项目(2017YFC0602903，2016YFC0600704，2016YFC0600709)；国家自然科学基金资助项目(51674012) (Projects(2017YFC0602903, 2016YFC0600704, 2016YFC0600709) supported by the Key Research and Development Program of China; Project(51674012) supported by the National Natural Science Foundation of China)

吴爱祥，博士，教授，从事矿山岩石力学及膏体充填研究；E-mail：wuaixiang@126.com