基于拍卖的订单接受与加工调度分散决策问题
2018-11-12朱倩倩王秀利耿苏杰
朱倩倩,王秀利,耿苏杰
(南京理工大学 经济管理学院,江苏 南京 210094)
0 引言
随着工业4.0时代的到来,个性化需求、批量定制正逐渐成为潮流,云制造作为一种面向服务的网络化制造新模式正越来越多地被制造企业采用,它是将现有网络化制造和服务技术同云计算、物联网等技术相融合,实现各类制造资源(机器设备、计算系统、数据等)的集中化和智能化管理,为制造全生命周期提供可随时获取、按需使用、安全可靠、优质低廉的各类制造活动服务,其核心思想是实现分散资源的集中使用和集中资源的分散服务[1]。
在云制造模式的分散决策场景下,制造商的订单接受与加工调度(Order Acceptance and Scheduling, OAS)问题也受到越来越多的关注。在分散系统中,制造商的OAS问题不仅受资源的约束,还受其他客户选择的约束,制造商和客户作为“理性人”,往往力图以最小经济代价获得自身的最大经济利益,但对于制造系统而言,由于个体的自利性,在机制缺失的情况下,个体竞争的均衡结果常常会降低系统资源配置的效率,从而导致系统全局目标恶化,即分散决策代价[2-5](Price of Anarchy, POA)。POA是用来描述分散决策下的系统结果与系统全局最优结果的关系,只有通过机制设计引导分散系统中的个体竞争行为才能减小POA,优化系统全局性能。Wang等[6]通过合同设计机制解决了一个制造商可内部加工或转包给代工企业加工订单的OAS分散决策问题,在假设所有订单与加工能力信息透明的情况下,设计固定报价加转移支付合同和数量折扣合同,实现分散决策下全局性能的最优化。然而,在实际的分散决策场景中,制造商和客户所掌握的订单与加工能力信息都是不完全的,因此对不完全信息下OAS分散决策问题的研究具有更重要的现实意义。
拍卖是一种基于参与者竞价的资源分配方式,能够有效解决OAS分散决策中的信息不完全问题。通过拍卖解决调度问题,就是将资源的使用时间作为商品分配给竞标者。近年来,拍卖在生产调度领域的应用取得了很多研究成果。Kutanoglu等[7]采用组合拍卖机器时间的方式来解决复杂资源调度问题,研究了基于加权拖期惩罚为目标的加工车间作业调度问题,发现了组合拍卖机制和基于拉格朗日分解之间的联系;Dewan等[8]研究了基于拍卖的分布式环境下动态加工车间作业调度问题,以最小化提前和拖期惩罚为目标,设计拍卖机制提高分散系统全局性能;Attanasio等[9]研究了拍卖机制在并行机调度中的应用,以最小化完工时间为目标,采用基于改进拉格朗日启发算法的拍卖机制优化全局性能;Hall等[10]研究了多个单件订单客户通过竞争制造商单机加工能力资源加工其订单的问题。文献[10]从基于加工时间的调度目标出发,设计了基于固定时段和灵活时段的升价拍卖(ascending price auction, 也称英式拍卖)机制,分析了该拍卖机制所生成的最终决策结果能够成为均衡解的条件。经研究发现,上述文献都采用传统调度度量目标(如订单完工时间、总加权滞后时间等),对于多主体企业追求收益目标而言具有一定的局限性。
在不完全信息的分散决策场景下,本文以明确的经济收益为目标,研究设计一种多轮升价拍卖机制来解决加工能力有限,但需要承诺交货期的OAS问题。在制造商和客户分别以最大化自身净收益为目标的前提下,通过设计合适的拍卖机制优化系统全局性能,使该分散系统决策结果尽可能接近完全信息下的系统全局最优解。
1 问题描述与建模
1.1 问题描述
假设制造商面对n个客户单件订单加工需求,已知每个订单i的加工时间为pi,交货期为di,市场加工收益为ri。假设制造商加工能力描述为单机(single machine),机器加工从0时刻开始有效,机器的加工时间被划分为时间槽集合{1,2,…,T},每个时间槽t表示时间段[t-1,t],制造商在任意时间槽只能加工一件订单,且订单加工不允许中断;已知每个机器时间槽t的加工成本为qt,它包括制造商为生产产品而发生的各项费用,如员工工资、机器折旧费、修理费等,制造商只有在生产所得收益能够抵补生产成本时才能确定盈利;制造商和客户所组成的分散制造系统中信息是不完全的;制造商不了解市场加工订单信息,包括订单市场收益、加工时间需求和交货期限承诺,同时客户也不知道制造商的加工成本信息。

1.2 完全信息下的系统优化决策问题
将一个制造商和若干客户组成的分散制造系统作为一个整体,考虑在完全信息下该制造系统的全局最优解,以优化系统净收益为目标,构建该问题的整数线性规划模型。假设市场客户订单集合N={1,2,…,n}需要加工,制造商拥有连续机器时间槽集合Α={1,2,…,T};所有订单i的加工时间pi和交货期di为正整数。定义决策变量xit∈{0,1},如果订单i在机器上加工且在时刻t完工,则xit=1,否则xit=0,其中i=1,2,…,n,t=1,2,…,T。该问题的整数线性规划(Integer Linear Programming, ILP)模型如下:
s.t.

(1)
∀t∈A;
(2)
txit≤di,∀i∈N,∀t∈A;
(3)
xit∈{0,1},∀i∈N,∀t∈A。
(4)
其中:约束(1)为订单约束,表示制造商接受订单,并且订单只能被加工一次,或者制造商不接受订单;约束(2)为机器约束,表示任意两个订单在机器上的加工时间不能重叠;约束(3)为订单交货期约束,表示被接受加工的订单必须按期完工交货。
假设每个机器时间槽的加工成本相同,即q1=q2=…=qT,就系统优化决策问题可以得到下列优化性质:
引理1存在一个最优决策方案,订单加工中间没有空闲时间直至所有被加工的订单完工。
引理1的结论是明显的,证明省略。
引理2存在一个最优决策方案,订单按交货期非减(Earliest Due Date First, EDD)规则排序。
证明假设存在最优调度π,其中交货期早的订单后加工。在该调度里,必须至少有两项相邻的订单j和k,订单j在订单k之前加工,使得dj>dk。假设订单j在时间t开始加工,对订单j和订单k执行所谓的邻对交换得到新的调度π′。在调度规则π下,订单j和k的完工时间分别为
t+pj≤dj,t+pj+pk≤dk。
在π′下,订单j和k的完工时间分别为
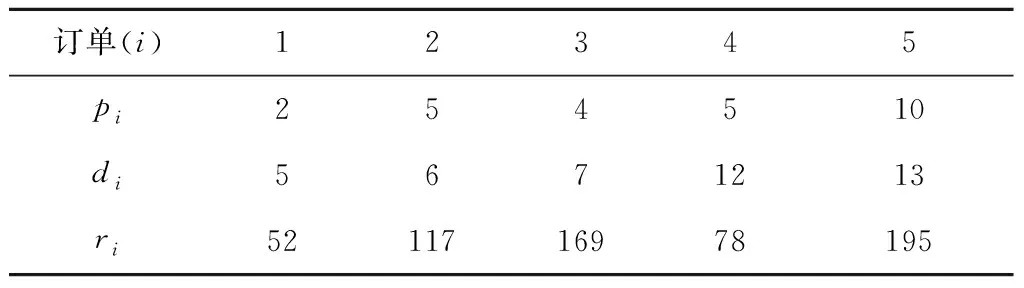
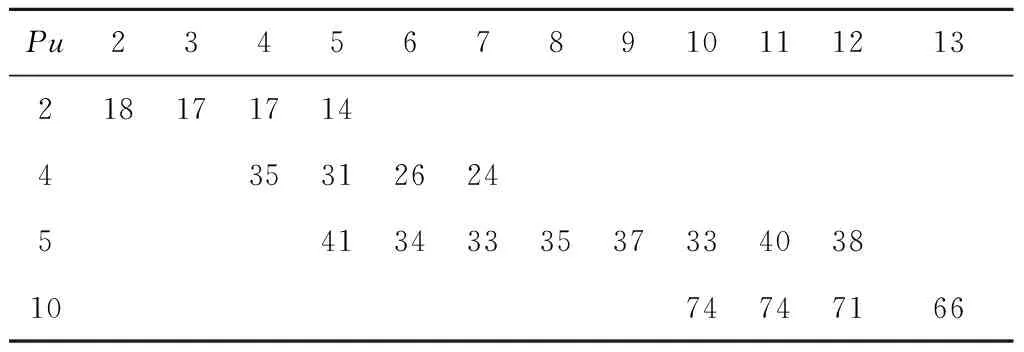
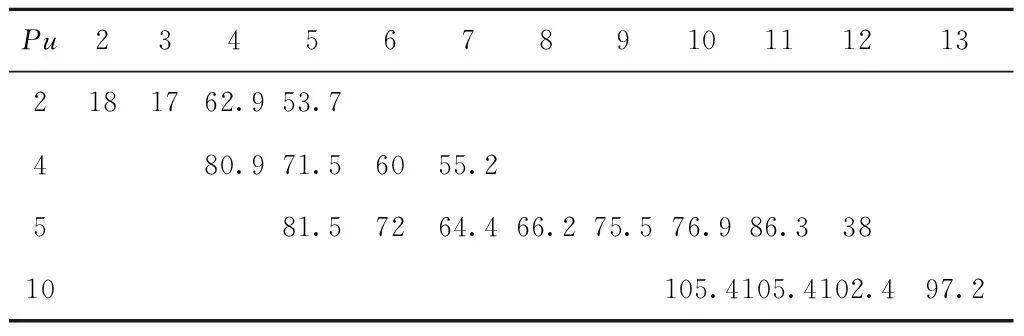
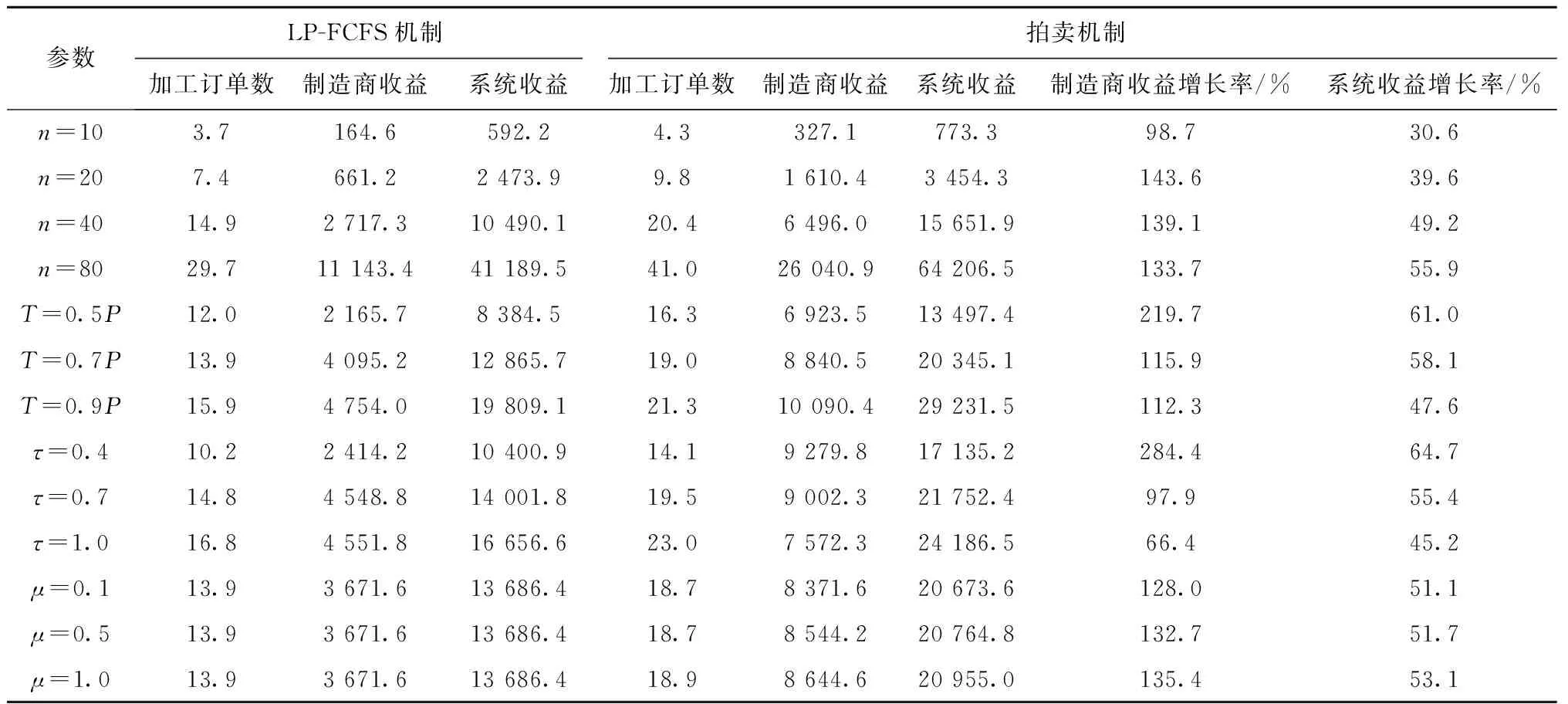
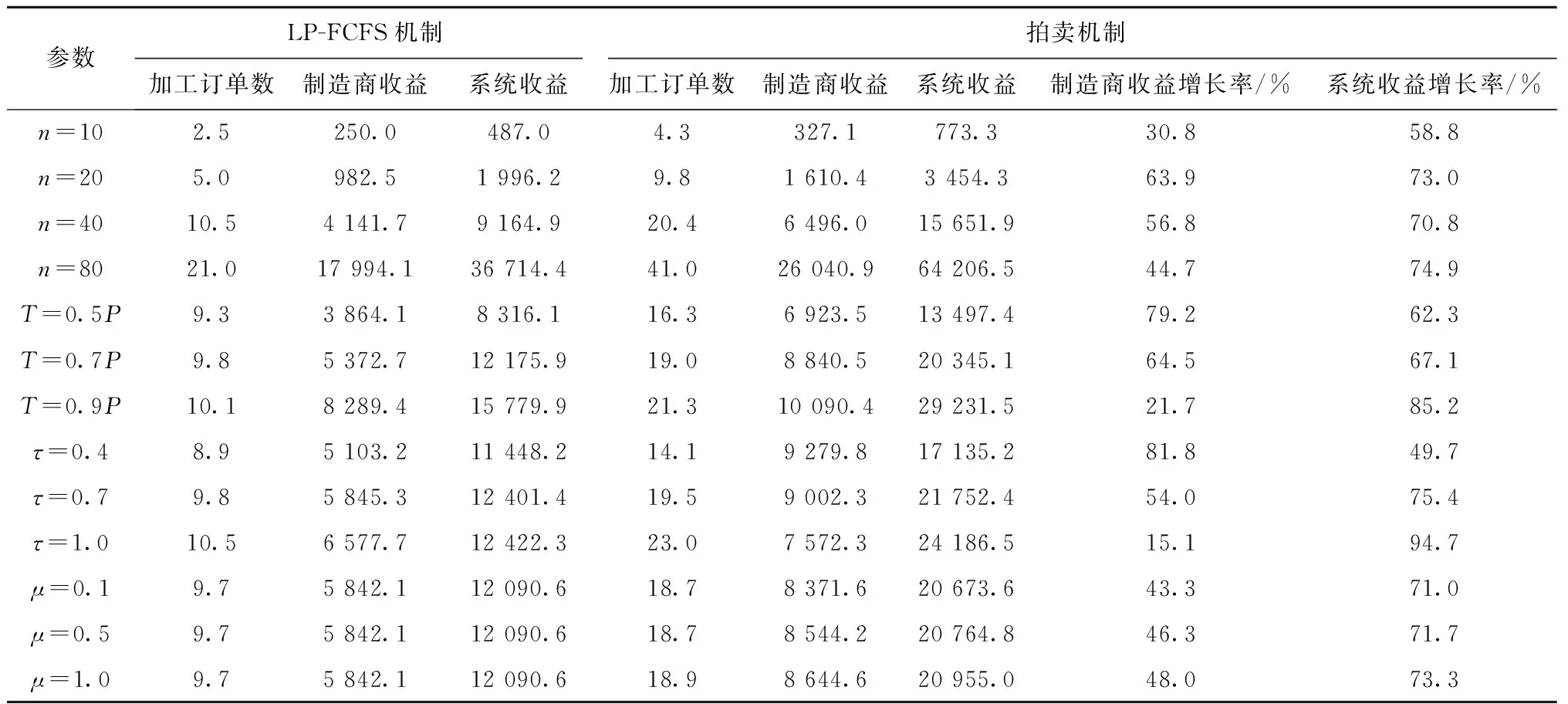
t+pk+pj≤dk 此时,调度π′仍然满足交货期要求,并且在制造商机器时间槽成本相同的情况下,调度π′也是最优调度。由此可见,存在一个最优调度,其中交货期早的订单先加工。证毕。 利用引理1和引理2,可以将qt(t=1,2,…,T)相同时的ILP模型用动态规划(dynamic programming)方法求解。 不失一般性,假设集合N={1,2,…,n}中的订单按交货期从小到大编号。令f(i,t)为制造商仅使用1,…,t时间槽的加工能力来选择性地加工订单1,…,i时的最大系统净收益。 边界条件为f(0,t)=0,t≥0。 递归方程为 s.t. pi≤t≤di 否则 最优解为f(n,T)。 需要说明的是,在订单加工顺序可以确定的情况下(可能不是EDD),该动态规划算法仍然适用。例如,在下述拍卖机制中,由客户投标决定订单加工顺序时,制造商的竞胜标问题仍然可以采用该动态规划算法求解。 制造商和客户组成的两阶段分散决策场景中,客户在已知制造商机器时间定价的情况下,通过投标竞争制造商机器加工时间来优化自身净收益;制造商在考虑客户投标的情况下,充分利用加工能力来优化自身净收益,为了实现制造商和客户的双赢,设计如下多轮升价拍卖机制。 将拍卖应用于调度问题,即通过拍卖来分配制造商的生产能力,制造商即可描述成“拍卖者”,制造商的机器时间是“拍卖物品”,客户是拍卖中的“竞标者”。拍卖机制由制造商定价机制、客户投标机制和制造商竞胜标机制组成。当机器处于空闲时,制造商发出拍卖请求,客户通过投标来竞争机器时间,制造商则根据投标情况确定竞胜标,形成临时调度方案,制造商再根据临时调度方案和投标情况更新机器时间的价格,客户根据更新的价格决定新一轮的投标,如此反复,直至拍卖结束。拍卖的作用在于通过不断更新物品价格来引导客户需求,协调订单在机器上的加工,以减少资源竞争的冲突,提高系统资源配置的效率。拍卖的具体流程如下: (1)给定订单i(i=1,…,n)的加工时间pi、加工收益ri、交货期di;给定制造商的机器时间槽t(t=1,…,T)的加工成本qt。 (2)制造商向客户发出拍卖请求,并根据机器时间的加工成本、客户投标情况和临时调度方案构建拍卖时间段[u-p+1,u]的要价(Asking price)α(p,u)。 (3)客户i(i=1,…,n)根据要价α(p,u)确定投标Bi(pi,ui),bi,其中(pi,ui)表示客户所竞标的时间段[ui-pi+1,ui],bi表示投标价格,且投标价格不得低于时间段[ui-pi+1,ui]的要价α(pi,ui)。 (4)制造商收集所有客户的投标求解竞胜标问题,形成临时调度方案,并将中标客户的投标价格bi直接赋给中标价格β(pi,ui),如果在步骤(2)中没有一个客户竞标,则该临时调度方案即为最终的调度方案,拍卖结束;否则返回步骤(1)。 本文研究的单件订单接受与加工调度分散决策问题中的订单加工是不允许中断的,要求拍卖物品必须是连续机器时段的组合,这不同于常见的单一物品拍卖[11-12],也不同于拍卖物品可以任意搭配的组合拍卖[13-15]。因此,设计基于连续时段的自适应定价策略,不仅可以大大缓解资源供求冲突问题,还可以指导拍卖的动态调整,提高拍卖的效率。具体规则如下: 本文采用占优投标策略,即无论其他竞争对手采用何种策略,该策略对投标者都是最优的。投标分为两部分,客户不仅要决策出竞标的时间段,还要给出投标价格,投标以Bi(pi,ui),bi的形式给出,其中i=1,…,n。在2.1节的拍卖步骤(3)中,如果客户中标,则仍以同样的标参与下一轮竞争;如果客户未中标,则根据已更新的要价和投标规则给出新的投标,具体投标规则如下: 客户i以最大化自身净收益为目标,在尽可能保证中标的前提下,选出有最大竞争优势的竞标时间段(pi,ui),即(pi,ui)=argmax{ri-α(pi,pi),ri-α(pi,pi+1),…,ri-α(pi,di)}。 客户i的投标价格bi是在要价的基础上,根据自身的提价空间给出一定的加价,这个加价又称作竞价阶梯,记作λi。竞价阶梯可以由拍卖者决定,也可以由竞拍者决定,可以是固定的,也可以是不固定的。在现实中,每个物品的效用对不同的消费者来说是不同的,为了能够将客户的真实偏好信息反馈给制造商,以协调客户需求与制造商的生产能力,本文的竞价阶梯由客户(竞拍者)根据自身竞争能力决定,令λi=ρ(ri-α(pi,ui)),ρ∈(0,1)。 该占优投标策略可以确保客户中标的机器加工时间给其带来正的收益,并且是最大的净收益,这样的拍卖机制更易于得到客户的青睐。 制造商竞胜标问题是在客户的投标约束下,以最大化制造商净收益为目标,进行订单接受与加工调度决策。初始化收到的投标Bi(pi,ui),bi(i=1,…,n),不失一般性,假设投标Bi按ui升序编号。令f(i,t)为制造商仅使用1,…,t时间槽的加工能力选择性地加工投标B1,…,Bi所能获得的最大净收益。竞胜标问题的动态规划模型如下: 边界条件为f(0,t)=0,t≥0。 递归方程为 s.t. ui=t 否则 最优解为f(n,T)。 本文通过IBM ILOG CPLEX 12.3和Visual C++编程实现上述模型和算法,通过广泛的问题实例分析讨论理论结果的管理启示。具体的,计算实验主要分析讨论拍卖机制的价值和性能,包括该拍卖机制对分散系统提高收益的价值,分散决策相对于系统全局集中的代价,以及各种参数的变化对拍卖性能的影响。 已知该算例包括5个客户单件订单加工需求,具体的订单信息如表1所示,制造商的加工能力和加工成本信息如表2所示。拍卖由制造商定价、客户投标和制造商竞胜标组成,具体拍卖步骤如下: (1)第1轮 首先,已知制造商机器时间槽成本qt,计算机器时间槽报价α(p,u),如表3所示;然后,根据计算机器时间槽报价α(p,u),客户进行投标,如表4所示;最后,制造商根据上一步的投标计算竞胜标,得出投标B3(4,7,53)中标,制造商收益为29,系统收益为145。令β(4,7)=53,μ=1。 ZHANG Heng, WU Lin-lin, LI Shi-jie, KUANG Ye, MA Xing-hong (2)第2轮 根据2.2节定价策略重新计算α(p,u),如表5所示;紧接着,客户根据α(p,u)再次进行投标,如表6所示;根据第2轮投标计算竞胜标,得出投标B1(2,3,24)和B5(10,13,116.8)中标,制造商收益为57.8,系统收益为164。令β(2,3)=24,β(10,13)=116.8,μ=0.5。 (3)第3轮 投标B1(2,3,24)和B3(4,7,128)中标,制造商收益为111,系统收益为180。计算方法和第2轮相同,此处省略。 (4)第4轮 投标B1(2,3,24)、B3(4,7,128)和B4(5,12,46)中标,制造商收益为119,系统收益为220。计算方法和第2轮相同,此处省略。 (5)第5轮 投标B1(2,3,24)和B5(10,13,181.4)中标,制造商收益为122.4,系统收益为164。计算方法和第2轮相同,此处省略。 此时,没有新的投标出现,拍卖结束,最终调度结果为从时间2开始加工订单1,从时间4开始加工订单5。 表1 订单加工信息 表2 制造商机器时间槽成本 表3 第1轮机器时间槽报价α(p,u) 表4 第1轮客户投标Bi 表5 第2轮机器时间槽报价α(p,u) 表6 第2轮客户投标Bi 本文分别对订单个数n=10,20,40,80的4种情况随机生成问题实例,生成的问题实例规则如下: (2)制造商的要价根据3.2节的自适应定价规则确定,价格增量系数μ∈{0.1,0.5,1.0},竞价阶梯系数取ρ=0.2。 (3)客户投标价格按照3.3节的投标规则确定。根据以上参数设计可以形成108个组合,对于每种组合分别生成10个问题实例。 本文设计的拍卖机制能够有效地解决分散决策场景下的OAS问题,在信息不完全的情况下,通过自适应定价规则引导拍卖的动向,实现系统资源的有效配置,提高系统全局收益。实验将拍卖机制与先来先服务(First Come First Served,FCFS)订单加工策略进行对比,以分析拍卖机制对制造商和客户收益的影响。 假设在信息不完全的分散决策场景下,制造商按照订单到达顺序,依次选择并接受可以按期不亏本加工的订单,并以高于加工成本的价格向客户收取一定的订单加工费用,最常见的制造商定价方式是线性定价(Linear Pricing, LP),制造商获得的加工收益为所接受订单的总收入减去总加工成本。基于制造商线性定价的先来先服务(LP-FCFS)机制既能保证公平性又简单易行,因此被工业界广泛使用。但是,由于制造商和客户之间信息的不完全,制造商和客户都无法做出有利于各人和整体利益的决策。 表7 拍卖机制与LP-FCFS(δ=1.5)机制的制造商收益和系统收益 表8 拍卖机制与LP-FCFS(δ=3)机制的制造商收益和系统收益 为了揭示拍卖的性能,将拍卖机制与2.2节完全信息下的集中系统优化策略进行对比,计算分散决策代价(POA),即拍卖机制下的系统收益与集中优化的系统收益的比值,结果如表9所示。该拍卖机制总体表现良好,平均比值达到92.7%。另外,各个参数的变化对拍卖性能的具体影响如下:代表订单个数、制造商加工能力、订单交货期和拍卖自适应定价幅度的4个参数对拍卖性能均有明显影响,其中,随着订单个数n、订单加工能力T和订单交货期τ的增加,拍卖性能均明显提升;随着拍卖自适应定价参数μ的增加,拍卖性能明显下降;自适应定价系数μ对资源的需求感知越敏感,拍卖性能越好。 从表9还可以看出,该拍卖机制的计算性能良好,平均经过12.7轮,拍卖结束。其中,订单个数和自适应定价系数对拍卖轮数影响较明显,随着订单个数的增加和自适应定价系数的减少,拍卖轮数明显增加;制造商加工能力和订单交货期对拍卖轮数的影响不是很明显。 综上所述,拍卖机制总体性能良好,而且资源越紧缺,拍卖机制的优越性越明显,拍卖机制能通过动态价格引导更明显地分散资源需求,在有限时间内均衡配置稀缺资源。 表9 分散决策代价(POA)和拍卖轮数 本文根据分散决策下OAS问题的特点,设计多轮升价拍卖机制。制造商可以在不了解资源对客户的价值和具体使用细节的情况下将资源有效地分配出去,解决了分散决策场景下的信息不完全问题;该拍卖机制可以匿名操作,分散系统中的客户只需要根据自己的目标和约束进行占优投标决策,保证了客户估价的真实性,也易于被客户接受;该拍卖机制可以根据供求关系动态调整定价以达到竞争均衡;最后通过数据实验表明,该拍卖机制对解决OAS分散决策问题具有良好的效果。 本文设计拍卖机制解决单机环境下的OAS问题,后续研究可以扩展到现实中常见的并行机OAS问题,并针对具有NP难属性的并行机OAS问题设计基于启发式规则的竞胜标确定算法以提高拍卖机制的计算效率和实际应用性。
2 拍卖机制设计
2.1 拍卖流程

2.2 自适应定价策略



2.3 投标规则
2.4 竞胜标确定问题

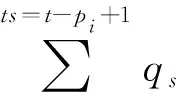
3 计算实验及分析
3.1 算例



3.2 数据生成

3.3 拍卖的价值
3.4 拍卖的性能

4 结束语
