基于PBIL算法的炼钢生产低碳调度问题
2018-11-12张燕华陈伟达孟祥虎
张燕华,陈伟达,孟祥虎
(1.东南大学 经济管理学院,江苏 南京 211189;2.西藏民族大学 信息工程学院,陕西 咸阳 712000;3.东南大学 自动化学院,江苏 南京 211189)
0 引言
2014年11月12日,中美发布的联合声明中提到:中国计划到2030年达到二氧化碳排放峰值,并争取提早实现这一目标。国家发改委宣布,我国将在2017年启动全国碳排放权交易市场。由于全球碳排放限额和交易机制的建立[1-3],排放权势必成为企业生产运作过程中必须考虑的要素,企业在制定生产调度方案时不得不将碳排放因素考虑进去。综观以往经验,大多是通过机器和设备改进的方式来降低能源消耗,减少碳排放。但实际上,制造业中设备空转时所消耗的能源占总能源消耗的比重很大,其中产生的碳排放量不可低估,然而现有研究却往往忽略了这一方面,生产调度优化目标大多集中在总完工时间最小[4]及其他成本指标最小等,而未考虑碳排放这一关键影响因素。钢铁企业作为长期以来的排污大户,合理安排其生产调度方案对企业实现节能减排有重要意义。
针对生产调度层面的碳排放研究才刚刚起步,相关文献较少。Fang等[5]以峰值功率、总完工时间和碳排放为目标,对两个机器的加工系统进行了实例分析,并采用多目标混合整数编程方法求解,但因多目标调度问题的复杂性而仅适合小规模问题的求解;Li等[6]考虑含碳化合物减排问题,对原来的以单一成本最小化为目标的汽车行业调度模型进行改进,通过使用替代能源的调度方案实现综合目标最优;Liu等[7]针对批处理建立了总拖期惩罚和碳排放的双目标优化模型,针对批处理机和并行机建立了总拖期惩罚、碳排放和峰值负载的多目标优化模型,并采用多目标遗传算法对问题求解,进而对影响环境指标的因素进行分析。
炼钢生产调度问题已经受到国内外众多学者的广泛关注。李铁克等[8]针对炼钢连铸生产过程建立了混合整数线性规划模型,将严格连续浇注作为等式约束,并采用遗传算法(Genetic Algorithm, GA)与线性规划(Linear Programming, LP)结合的两阶段遗传算法对问题进行求解;Tang等[9-10]将炼钢连铸生产抽象为三阶段混合流水车间调度问题,建立了整数规划模型,将拉格朗日松弛、启发式算法和动态规划相结合对模型进行求解;Tan等[11,12]考虑不同时段的电力价格变化,建立了以浇次为单位且生产时间可控的能源成本最小化模型,并采用启发式与约束传播的混合算法对模型进行求解。
炼钢生产过程需要高温连续作业,其生产调度过程中对工件在工序间等待时间有上限要求[13]。文献[8-10]将所有工件的等待时间之和最小化,而
未满足工件在工序间等待时间受限的条件。不同于传统的基于种群更新的进化算法,种群增量学习(Population-based Increased Learning, PBIL)算法采用概率模型学习采样,对解的基因位执行概率选择操作,能够有效地根据概率大小避开劣质解空间,使种群搜索更具针对性[14-15]。孟祥虎等[16]针对带时间窗车辆路径问题,提出混合种群增量学习算法,同时优化车辆数和总行驶距离;金炳尧等[17]针对旅行商问题以系统熵为结束进化计算判据,采用双值基因位的十进制编码PBIL算法求解;汪存富等[18]结合城市连接关系,采用十进制编码的PBIL算法求解非对称旅行商问题。
综上所述,炼钢生产调度的研究均以经济指标或工艺约束为优化目标,未考虑碳排放。本文针对等待时间受限的炼钢流程构建低碳调度模型,以最小化Makespan和CO2排放为优化目标,通过加权效用函数和标准化处理将其转换为单目标,并采用PBIL算法对问题进行求解。最后结合生产实际数据进行仿真实验,根据决策者对两个目标的不同权重组合进行若干组实验,并对实验结果进行分析。
1 炼钢生产低碳调度模型
1.1 问题描述
炼钢生产过程如图1所示,n个作业依次经过S道工序,每道工序有相同的Mj台机器。钢铁工业对钢包温度有严格要求,以避免因不满足工艺要求造成的重调度,因此所有作业的等待时间都受上限约束。炼钢生产可以抽象为等待时间受限的混合流水车间调度问题,该问题属于NP-hard问题。机器在作业间空转时会造成能量损失和碳排放,作业在工序间等待时也会因散失热量而产生碳排放。等待时间既是生产调度的约束条件,也是影响碳排放的因素之一。本文研究如何安排作业在各个工序上的机器分配及顺序,在满足约束条件的同时最小化Makespan与CO2排放指标。

1.2 符号定义
j为工序编号,j∈{1,2,…,J};
i为作业编号,i∈{1,2,…I};
mj为工序j的机器编号mj∈{1,2,…,Mj};
tijk为作业i在工序j的第k个机器上的标准加工时间;
sij为作业i在工序j的开工时间;
cij为作业i在工序j的完工时间;
NE(i,j)为工序j的机器在加工完作业i后要加工的下一个作业编号;
Xijk为1,如果作业i被指派到工序j的第k个机器上,否则为0;
Yi1i2j为1,如果作业i1和i2在工序j的同一机器上加工且i1先于i2被加工,否则为0;
Pjk为工序j的第k台机器在生产运行模式下的功率;
PIjk为工序j的第k台机器在空闲状态下的功率;
β为作业的等待时间上限;
c为钢水的比热容;
m为钢水的质量。
1.3 模型的建立
(1)将生产调度中产生的二氧化碳排放量作为目标函数f1
炼钢生产调度过程中产生的碳排放主要有3部分,即机器加工作业产生的碳排放、机器空转产生的碳排放、作业因等待散失热量产生的碳排放。作业在各工序机器上加工的能耗总和乘以碳排放系数得式(1)所示的碳足迹,其中ε表示电的碳排放系数。每个工序的机器在加工两个相邻作业间空转时间乘以其空转功率,再转化为碳排放,如式(2)所示。
(1)
(2)
假设降低的温度与等待时间成正比,系数为α,将所有作业在相邻工序间等待时间转换为散失的热量,进而求出其碳排放,如式(3)所示:
Wco2=εcmαTw/q;
(3)
式中q表示单位电能产生的热量,为3 600 KJ/kWh。式(4)表示所有作业的等待时间,式(5)表示所有炉次驻留过程中散失的热量。
(4)
Q=cmαTw。
(5)
炼钢生产调度中产生的碳排放为
f1=EBco2+EIco2+Wco2。
(6)
(2)将最小化最大完成时间作为目标函数f2
makespan=max{cij}。
由以上两个优化目标得到的炼钢生产低碳调度双目标数学模型如下:
minf1=EBco2+EIco2+Wco2;
minf2=makespan。
(7)
s.t.
si,j+1-cij≥0,
∀i∈{1,2,…,I},∀j∈{1,2,…,J};
(8)
si2j-ci1j+(3-xi1jk-xi2jk-yi1i2j)U≥0;
(9)
∀i∈{1,2,…,I},∀j∈{1,2,…,J};
(10)
yi1i2j+yi2i1j=1,
∀i1≠i2,∀j∈{1,2,…,J};
(11)
si,j+1-cij≤β,
∀i∈{1,2,…,I},∀j∈{1,2,…,J};
(12)
xijk∈{0,1},∀i,
∀j∈{1,2,…,J},∀k∈{1,2,…,Mj};
(13)
yi1i2j∈{0,1},
∀i1≠i2,∀j∈{1,2,…,J}。
(14)
这是一个双目标优化模型。式(7)表示目标函数,优化目标是最小化碳足迹与最大完成时间;式(8)表示同一个作业只有前一工序加工完才能开始下一工序;式(9)表示机器同一时刻最多加工一个作业,其中U表示足够大的正整数;式(10)表示每个作业在每个工序只能被一台机器加工;式(11)表示每个阶段任意两个不同的作业存在加工的先后关系;式(12)表示每个作业的等待时间不能超过时间上限;式(13)和式(14)表示变量的取值范围。
1.4 模型转换
以上数学模型是一个双目标优化模型,本文采用加权效用函数将其转换为单目标进行求解。加权和方法主要是将多目标优化中的各个目标函数乘以权重系数后求和,从而转化成单目标优化问题,其定义为:对于给定的m个优化目标fi(x),i=1,2,…,m,可转化为
(15)
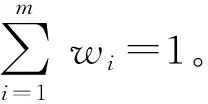
由于文中的目标函数f1与f2单位不同(前者是质量单位,后者是时间单位),要对其做标准化处理以消除量纲,这里采用“中心化”方法。经过标准化处理后得到的目标函数为
min (w1f1′+w2f2′)。
(16)
式中f1′和f2′是分别对f1和f2做标准化处理后得到的目标函数,每个标准化目标fi′都被定义为fi′=(fi-μi)/σi,对每个单目标fi取n(n足够大)个最优解作为样本空间,求出其均值μi和方差σi。
2 算法设计
本文采用PBIL算法对问题进行求解。PBIL算法结合炼钢生产流程建立3维矩阵和新的更新机制,利用概率模型产生每代种群。由于作业在相邻工序间的等待时间受到上限约束,采用PBIL算法能有效根据概率大小避开劣质解空间,使种群搜索更具针对性,从而获得问题的优良解。
2.1 编码方式

2.2 算法步骤

(17)
步骤2令k=1,各作业随机得到排序γk=[γk[1],γk[2],…,γk[l],…,γk[n]]。
步骤3给γk中的每个作业分配其被加工的机器,得到排序ζk=[ζk[1],ζk[2],…,ζk[l],…,ζk[n]],其中ζk为γk对应的加工机器排序。
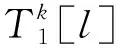


(18)
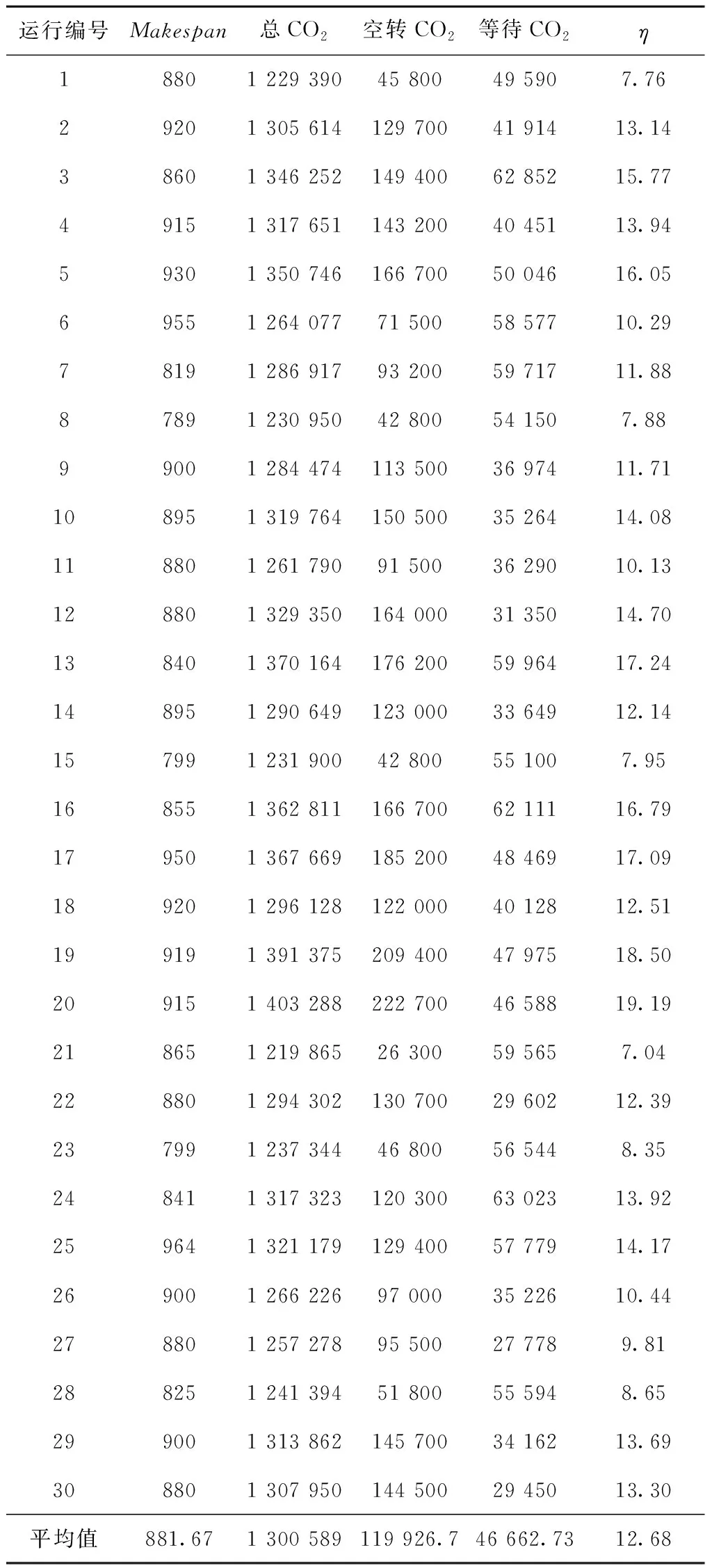
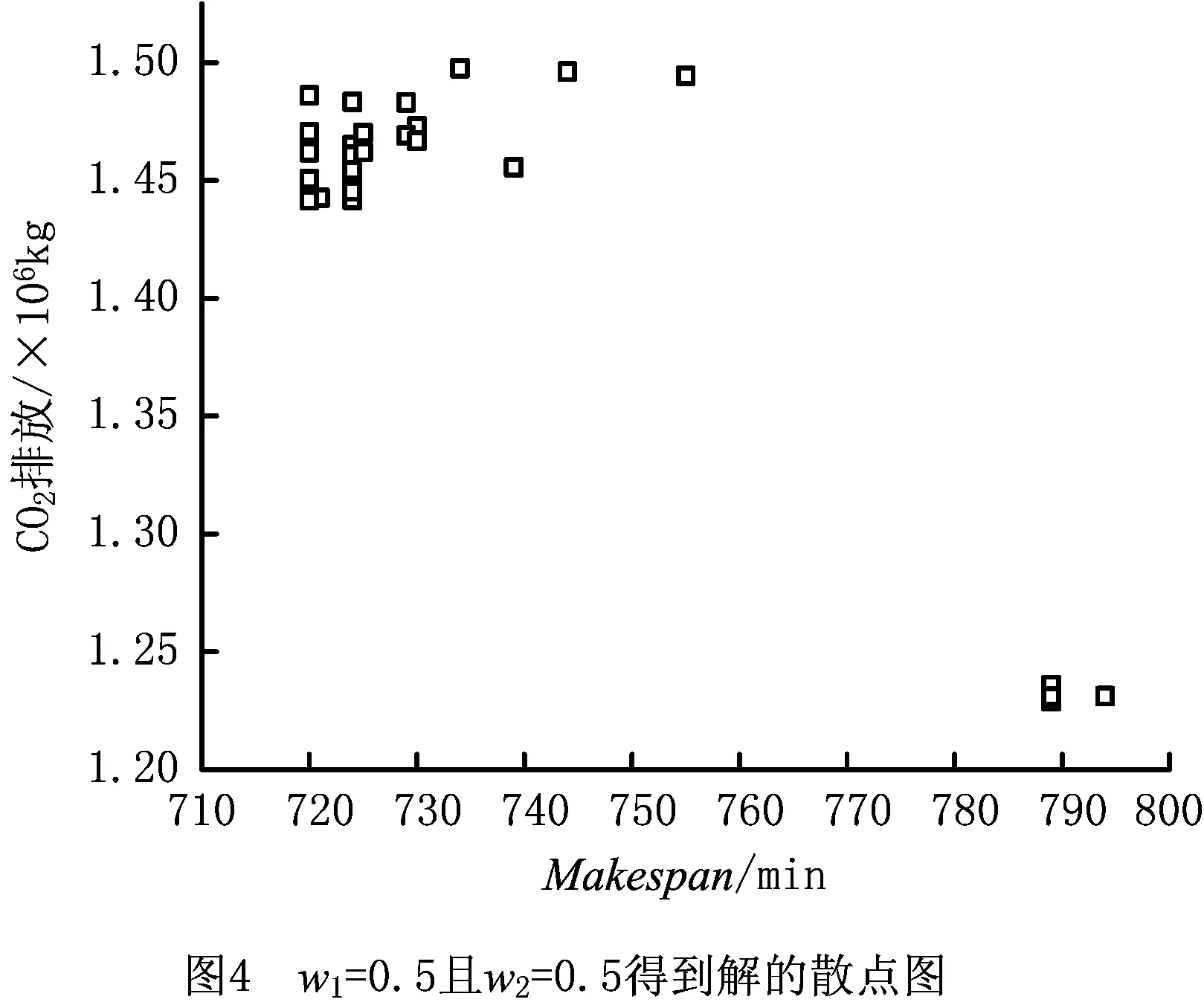
(5)若l i=γk[l],l=1,2,…,n; (19) i=γk[l],l=1,2,…,n。 (20) 步骤6若不满足结束条件,转步骤3;否则结束算法,输出结果。 以某钢厂电弧炉炼钢过程为例,电弧炉能力为80 t,采用超高功率加热;24个作业在3个阶段运行,每个阶段的机器数分别为2,3,2;所有作业在各阶段的运行时间、机器运行功率和空转功率数据如表1所示,作业在相邻阶段间的等待时间上限β=10 min;实验参数设置为种群规模popsize=30,学习速率θ=0.01,最大进化代数为1 000;机器加工作业产生的能耗和碳排放是定值,机器空转与等待产生的碳排放受不同调度方案的影响,用η=(EIco2+Wco2)/f1表示因调度产生的碳排放占总碳排放的比例,其中EIco2表示空转CO2,Wco2表示等待CO2,f1表示总CO2。 表1 作业加工时间与机器功率 注:[]中的数字依次为最小加工时间和最大加工时间。 Makespan与CO2排放两个目标的权重值由决策者确定。若决策者看重能量消耗和碳排放,则取较高的w1;若决策者看重经济指标,则取较高的w2。根据不同的决策方案做如下几组实验: 实验1当决策者只注重经济指标时,权重组合取w1=0且w2=1。 将程序运行30次,得到表2所示结果,图2所示为解的散点图。从图2可见,Makespan的值在717~735之间,对应的碳排放集中在1 450 000~151 000之间,存在Pareto前沿解集,运行编号3,27,29的解存在反相关关系。从表2可见,当Makespan取最小值719时,对应的CO2排放介于1 467 633~1 474 105之间;当CO2排放取最小值1 447 338时,对应的Makespan增加到724,编号29的结果介于这两个解之间。当决策者只优化经济指标Makespan时,造成高的能量损耗,由空转和等待造成的碳排放比例最高达到25.07%,其中空转时间为主要影响因素。 当决策者只关注经济指标Makespan时,调度方案造成约占总能耗1/4的能量损耗和碳排放,决策者必须采取有效措施减少能量损耗和碳排放,最简单的方法是空转时关掉机器。但废钢铁再制造过程需要高温作业,关机造成温降,下次开机需重新预热,再次造成能量损失。 表2 w1=0且w2=1得到Makespan与CO2排放相关数据 运行编号Makespan总CO2空转CO2等待CO2η/%17201 479 786326 90018 88623.327491 513 491353 10026 39125.0737241 447 338298 10015 23821.6547301 490 967336 20020 76723.9457201 494 865341 20019 66524.1467191 470 143319 10017 04322.8677401 488 122324 90029 22223.8087291 492 715338 10020 61524.0397251 503 813348 40021 41324.59107191 471 510320 60016 91022.94117251 486 575331 20021 37523.72127191 469 510318 60016 91022.83137241 478 728327 40017 32823.31147301 509 724354 90020 82424.89157191 471 232319 60017 63222.92167351 505 341345 90025 44124.67177241 484 961331 60019 36123.63187291 493 877339 30020 57724.09197191 474 105323 10017 00523.07207301 503 536345 90023 63624.58217241 483 492331 10018 39223.56227201 473 314322 10017 21423.03237351 474 096315 70024 39623.07247291 472 976316 10022 87623.01257251 470 223316 90019 32322.87267191 471 232319 60017 63222.92277191 467 633316 40017 23322.73287301 487 410332 70020 71023.76297201 453 521299 40020 12121.98307251 483 182328 70020 48223.54平均值725.831 482 247328 093.320 153.9323.49 实验2当决策者只注重能量消耗与碳排放时,权重组合取w1=1且w2=0。 将程序运行30次,得到表3所示结果,图3所示为解的散点图。从图3可见,Makespan主要在790~960之间,对应的碳排放在120 000~40 000之间,运行编号8和21的解是Pareto前沿解集。从表3可见,由机器空转和等待时间造成的碳排放比例最低降到7.04%;与实验1的结果相比,碳排放平均值减少了181 658 kg,η减小了12%,但Makespan平均增加了156。当生产任务不紧张时,选择该方案可最大限度减少能源消耗和碳排放。 表3 w1=1且w2=0得到Makespan与CO2排放相关数据 与实验1相比,等待碳排放平均增加26 509,但空转碳排放平均减少208 167,约减少2/3,是影响总碳排放的主要因素。等待时间既是生产调度的约束条件,又是影响碳排放的因素之一,从实验结果可见,空转时间的减少导致等待时间增加,但等待时间受到的约束不能超过上限值。因此等待时间受限的混合流水车间调度很难满足既无空转时间又无等待时间的条件,而且随着工件数的增加,调度问题更为复杂。 实验3当决策者同时注重Makespan和碳排放指标时,权重组合取w1=0.5且w2=0.5。 程序运行30次,得到表4所示结果,图4所示为解的散点图。从图中可见,所有解主要集中在两个区域,左上角区域的Makspan相对较小,但是碳排放比较大,右下角区域碳排放小,但Makspan较大,Makspan与CO2明显呈反相关关系。该方案得到两个目标值的平均值介于实验1与实验2之间。当决策者需要同时优化两个目标,每个目标都不能达到最优值时,在生产任务和节能减排双重压力下可以选择该方案。 表4 w1=0.5且w2=0.5得到Makespan与CO2排放相关数据 运行编号Makespan总CO2空转CO2等待CO2η/%17241 465 118313 60017 51822.6027241 448 758296 10018 65821.7337551 494 292326 70033 59224.1147241 445 338296 10015 23821.5457241 441 682292 90014 78221.3467201 444 526292 40018 12621.5077891 228 95040 80054 1507.7387241 483 279327 60021 67923.5597301 472 902320 70018 20223.01107201 441 606292 90014 70621.34117241 454 343297 60022 74322.03127201 441 606292 90014 70621.34137441 496 087337 90024 18724.20147201 441 606292 90014 70621.34157891 235 89446 30055 5948.24167291 469 043316 10018 94322.81177341 497 496339 10024 39624.27187241 460 833309 60017 23322.37197201 448 486299 40015 08621.71207201 448 836296 90017 93621.73217201 464 766313 40017 36622.58227891 230 95042 80054 1507.88237291 483 099325 90023 19923.54247251 462 089310 40017 68922.44257201 470 386319 40016 98622.88267241 441 834292 90014 93421.35277201 486 057334 90017 15723.69287201 445 026292 90018 12621.52297201 441 606292 90014 70621.34307251 470 071316 90019 17122.86平均值731.71 438 552282 363.322 188.821.0 实验4将w1,w2以0.1为间隔且w1+w2=1分别取值(0,1)、(0.1,0.9)、(0.2,0.8)、(0.3,0.7)、(0.4,0.6)、(0.5,0.5)、(0.6,0.4)、(0.7,0.3)、(0.8,0.2)、(0.9,0.1)、(1,0)。每种组合情况将程序运行30次并求目标值的平均值,得到11个点的散点图,如图5所示,可见两个目标值之间存在反相关关系。 本文针对等待时间受限的炼钢生产调度问题,设计了碳排放计量方法,建立了最小化Makespan和碳排放的双目标优化模型,用加权效用函数与标准化方法将其转换为单目标,采用PBIL算法对问题求解。结合实际生产数据的仿真实验发现:①当决策者只注重经济指标Makespan时,将导致较大的能量损耗和碳排放;②当决策者只注重碳排放指标时,空转产生的能量损耗减少了2/3,等待时间因受上限约束增加不大,此时Makespan增加;③当决策者同时重视Makespan与碳排放指标时,两个目标值都能得到优化,但都不能达到最优值;④对11组权重值进行实验,可以明显看到两个目标的反相关关系。 在碳权交易市场机制下,碳价的变化影响碳排放成本,钢铁企业在安排生产调度方案时不得不考虑碳排放因素。若生产任务紧张,则应考虑如何减少空转能量损耗,如空转时调低机器功率,既保证设备高温又可减少能量损失;若市场需求低迷,则决策者以Makespan增加为代价而最优化碳排放目标,既不影响生产任务又实现了节能减排;若情况介于前两者之间,则决策者可将Makespan目标与碳排放目标的权重组合设置为(0.5,0.5),从而获得折中的调度方案。今后可进一步考虑机器故障等因素的干扰,研究基于动态的节能调度优化方法。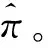
3 仿真实验






4 结束语
