曲梁柔性铰链性能分析及应用机构设计
2018-11-12陈应舒朱淳逸
陈应舒,朱淳逸
1 引言
柔性铰链是柔顺机构中重要的组成部分。随着柔顺机构的在微精密机械、光学、医学等领域的快速普及使得对柔性铰链的研究逐渐引起了国内外众多研究人员的重视。近十几年来人们对柔性铰链的研究逐渐细化,各种形状各异的柔性铰链被提出与研究。目前,对直梁型柔性铰链的研究最为透彻,不论是文献[1]所提到的深切口椭圆柔性铰链,文献[2]中的圆弧形柔性球铰,还是文献[3]中所提及的单边型柔性铰链。从本质来看,这些均为等截面或变截面的直梁。国内外文献对于直梁柔性铰链的分析研究方法也已经相当完备。对直梁柔性铰链的应用也是做了大量研究,如文献[4]设计了一种基于柔性铰链的微位移放大机构;文献[5]设计并分析了一种三自由度的精密定位平台等等。
考虑到设计要求与工作场合等实际情况,单纯使用直梁柔性铰链作为铰链单元所组成的柔顺机构可能并不能满足某些工作需要。而曲梁柔性铰链是柔性铰链作为梁弯曲的中性面在自然状态之下呈现曲面的一类柔性铰链,能够为丰富柔顺机构的设计思路,对柔顺机构的设计提供一些构型上的补充。近年来,也有相当一部分文献对曲梁柔性铰链的相关性质进行了研究,文献[6-8]使用椭圆积分法对大变形状态下的曲簧片进行了力学分析;文献[9]对曲梁三角柔性铰链进行了力学建模与分析;文献[10]对铁摩辛柯梁理论变形下的曲梁柔性单元平面外弯曲与扭转锁定现象进行了分析等等。研究了等截面圆弧曲梁柔性铰链,基于线弹性与小变形理论以及欧拉伯努利梁理论,利用卡氏第二定理给出了圆弧曲梁柔性铰链的柔度矩阵公式,并选取了合适几何点给出了精度公式。并使用有限元分析软件ANSYS14.0对柔度公式进行了简单的验证。
设计建立了一种应用曲梁柔性铰链的多环平行导向机构模型,该平行导向机构区别于其他平行导向机构的地方在于其可以水平和竖直两个方向上进行导向,该机构可以应用于某些精密测量装置中完成对正交物理量的测量。
2 曲梁柔性铰链
直梁柔性铰链,如图1所示。常见的有直梁型、圆弧形、单边型等几种类型。

图1 三种常见的柔性铰链Fig.1 Three Common Kinds of Flexure Hinge
其共同特点为中性面为平面。而曲梁柔性铰链,如图2所示。

图2 曲梁柔性铰链Fig.2 Curve Beam Flexure Hinge
由图可知,曲梁柔性铰链的中性面为曲面。由于一般的曲梁柔性铰链的弯曲变形在理论计算的复杂性,只选择最简单的圆弧曲梁给出其柔度矩阵公式。
2.1 圆弧曲梁柔度矩阵公式推算

图3 圆弧曲梁铰链参数模型Fig.3 Parameter Model of Circular Arc Curve Beam Hinge

圆弧曲梁详细的参数模型,如图3所示。为曲梁在任意径向截面下的惯性矩,A=(b-a)l是曲梁任意径向截面的面积。E为弹性模量。
2.2 曲梁柔性铰链的精度
柔性铰链的精度是除柔度之外重要的参数,柔性铰链的精度在一定程度上决定了整个机构的精度。对于直梁柔性铰链,国内外学者在计算铰链精度时普遍采用柔性铰链几何对称中心的位移来表示柔性铰链的精度。而精度模型随着选取的计算量的不同而不同。采用曲梁圆弧弧线中点处的柔度矩阵表示其精度,如图4所示。

图4 假想力示意图Fig.4 Schematic Diagram of Fictitious Force
在A点位置的施加一对垂直的假想力Fr、Fθ以及一个假想力矩MA,力Fr是指向弧线曲率中心的径向力,Fθ则是与弧线相切的切向力,对此应用卡氏第二定理可得:

3 有限元验证及性能分析
使用比较常用的45Mn钢作为柔性铰链的验证材料,此时E=200GPa。分别取 A:a=2mm,b=3mm,l=8mm;B:a=2mm,b=4mm,l=8mm;C:a=3mm,b=3.5mm,l=8mm;三组作为验证对象,分别将此三组数据带入理论公式计算和ANSYS有限元分析软件进行有限元分析。运用ANSYS进行有限元分析时在WORKBENCH里建立两条路径(Path1,Path2),如图 5所示。

图5 有限元分析图Fig.5 The Finite Element Analysis
利用近似计算公式θ=tanθ计算Path1的转角作为曲梁柔性铰链的转角,并将Path2在x、y轴方向上的位移作为曲梁柔性铰链分别在x、y轴方向上的位移。将理论公式计算结果和有限元分析对比结果列在表1中。由表1以可知:B组理论计算数据与有限元得到的数据相差较远,其根本原因是上述柔度计算公式是在忽略了剪力对变形造成的影响的条件下导出的,因此对于比较薄的梁结构柔性铰链,工程实践证明,大多数情况下都可以不考虑建立对变形的影响,因此针对薄臂长粱应用上述伯努利梁理论模型,能够得到较为精确地结果。而对于厚臂短梁结构柔性铰链,由于剪力对变形的影响比较大,大多数情况下,建立的影响不能被忽略,其分析计算已超出了上述公式的实用范围,因而不建议适用上面推导的理论公式进行分析计算。由以上柔度公式进一步分析可知:柔度公式的各个分量在形式上具有相似性,而柔度分量的大小主要与曲梁中性面的半径R,梁的厚度b-a,梁的跨度l有关系。
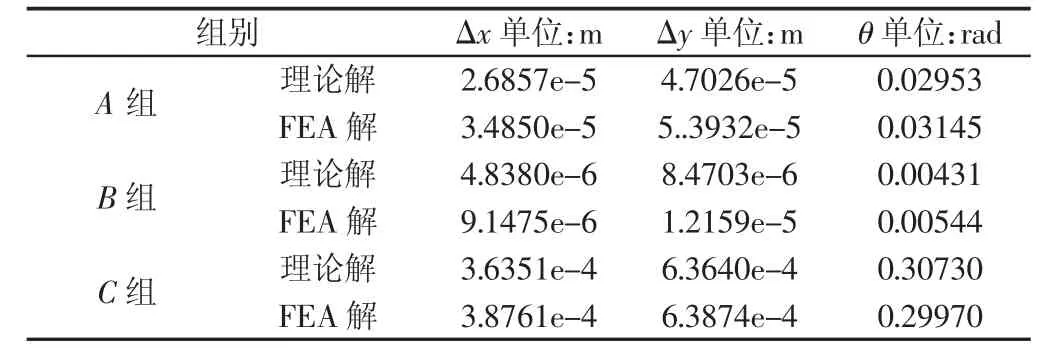
表1 理论解与有限元解结果对比Tab.1 Comparison of Compliances Between Theoretical Results and Finite Element Analysis Results
4 曲梁柔性机构的应用举例
曲梁柔性铰链的设计尺寸与角度相比直梁柔性铰链更加丰富,从而在柔性机构的某些结构的设计应用上更加丰富与方便。应用了曲梁柔性铰链的任意类型的四杆以及五杆机构,如图6所示。

图6 由曲梁柔性铰链所组成的机构Fig.6 Mechanism Made by Curve Beam Flexure Hinge
这些四杆机构能够实现更多单纯使用直梁柔性铰链设计的柔顺机构所不能完成的任务。而图7所设计的多环平行柔顺机构能够体现出曲梁相对于直梁在功能上的优越性。

图7 多环平行导向机构Fig.7 Parallel Guiding Mechanism with Multiple Links
该机构左边下方第一个杆件为固定杆。而在图示位置安装有两个与平行机构,如图7所示。

图8 水平力作用下的机构变形Fig.8 Mechanism Deformation Acted by Horizontal Force Fx
杆件紧密贴合的挡板,在自然状态下挡板与杆件没有相互作用力。两个挡板分别限制了与其:贴合的杆件的水平向左方向和竖直向下方向的运动,该机构在分别受到水平向右的作用力以及竖直向上的作用力时可以依靠曲梁柔性铰链的变形来实现两个垂直方向上的平行导向功能。受水平力作用时变形图,如图8所示。其中红色虚线部分为机构变形后的形状。当其受到竖直方向向上的作用力作用时,机构的变形情况,如图9所示。红色虚线部分为变形后的轮廓。由图8、图9的变形情况来看文章所设计的机构在水平方向的整体柔度与竖直方向上的整体柔度并不相同,但均可实现平行导向的功能。这一功能特点单纯应用直梁柔性铰链无法完成。该机构如果附加转动装置则可可以应用到某些精密检测装置或者精密仪器之中,完成对任意正交方向物理量的检测。
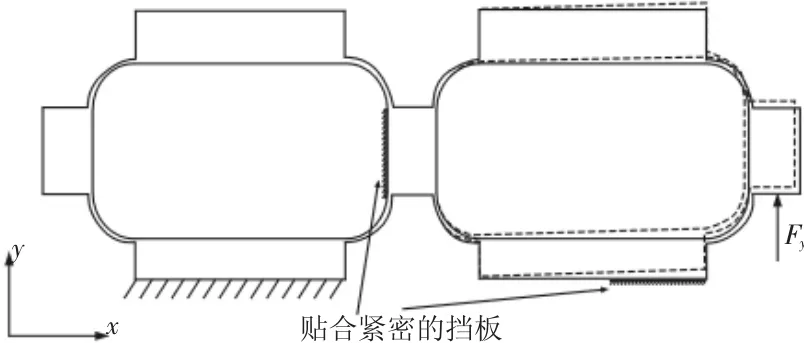
图9 竖直力作用下的机构变形Fig.9 Mechanism Deformation Acted by Vertical Force Fy
在UG中设计建立了上述平行导向机构以及固定底座的模型,如图10所示。
上述平行导向机构长度为10cm,宽度6cm,厚度为2cm。铰链厚度为1mm,内圆弧半径为3mm。将两个部件装配之后进行有限元分析,其分析结果,如图11所示。从缝隙结果可以看出,该机构可以满足双向平行导向的作用。

图11 平行导向机构的有限元分析Fig.11 FEA of Parallel Guide Mechanism
5 结论
基于线弹性和小变形以及欧拉伯努利梁理论,研究了等截面圆弧曲梁柔性铰链,运用卡氏第二定理给出了该柔性铰链的柔度矩阵公式以及精度公式。使用ANSYS进行了验证,有限元分析结果与理论值相比较表明,所推导的柔度公式在长而薄的梁铰链上运用足够精确;而对于短而厚的梁铰链,由于超出了本公式的使用范围,若勉强使用,则必然会出现较大的误差,因此不建议使用所导出的公式对短而厚的梁铰链进行分析计算。
所设计建立的应用曲梁柔性铰链的多环平行导向机构模型有别于其他平行导向机构的地方在于该机构由两个四杆机构使用一个公共杆件并联而成,其力学模型可以等效为长而薄的梁铰链结构。对该机构所进行的有限元分析结果表明:该机构既能够实现在水平方向上的平行导向又能够实现竖直方向上的平行导向。该机构如果附加转动装置则可实现任意正交方向上的平行导向功能。实验证明,利用所导出的公式进行分析计算的结果与实际实验的导向结果,其导能力及导向精度其导向精度基本吻合。
