固体推进剂花板浇注的数值模拟与实验研究

乌 岳，李 卓，鲁 荣

(1.内蒙古工业大学理学院，内蒙古 呼和浩特 010051；2.中国航天科工集团 内蒙古航天红峡化工有限公司，内蒙古 呼和浩特 010051；3.内蒙古工业大学化工学院，内蒙古 呼和浩特 010051)

引 言

固体推进剂药浆兼具黏性体和弹性体的双重特性，是典型的黏弹性非牛顿流体。固体推进剂低黏度药浆的浇注通常采用真空花板浇注工艺[1]，推进剂药浆流动的驱动力为料斗和浇注缸之间的压差以及料斗内推进剂药浆自重[2]。其本构方程和流动边界条件的复杂性，很难采用理论解析方法分析其流动[3]。目前随着计算机辅助技术的迅速发展，数值模拟已成为分析黏弹流体流动的主要手段。

姜爱民等[4]对固体推进剂药浆在混合釜内的流动过程进行了数值模拟，结合网格叠加技术和网格加密技术，对混合过程中药浆流动进行了有限元模拟，详细研究了捏合机混合过程中混合釜内剪切应力、各点的速度、混合指数、黏度的分布和极值关系；Connelly C K等[5]利用粒子示踪法，模拟了行星式混合内玉米糖浆的三维混合流动；Shimada T等[6]利用Polyflow软件将混有铅示踪颗粒的推进剂药浆浇注到一个透明型腔中，并在周围架设了两个方向的X射线透析仪器，通过计算得到药浆内颗粒的三维迹线，从而模拟得出比较直观的药浆内部的流场。

本研究利用黏弹性流体软件Polyflow提供的广义牛顿流体的本构模型，对复合推进剂药浆真空花板浇注流动的全过程进行数值模拟，针对真空花板浇注系统不同孔径的药浆流动速度、挤出胀大效应、药浆黏度和剪切速率及流平性做了一系列研究，同时通过实验对模拟结果进行了验证。

1 数值模拟

计算过程采用标准的CFD模拟分析流程：模型导入-划分网格-设置模型及参数-设置边界条件-利用CFD-POST对结果进行后处理。

1.1 推进剂浇注流动过程的基本假设

由于Polyflow软件本身的局限性，本研究依据实际情况作了以下假设：

(1)流动为低雷诺数的不可压缩流体的层流流动[7]，且流动过程不考虑推进剂药浆与外界环境的热交换(实际的浇注工房有循环水作保温)；

(2)推进剂药浆与壁面之间作无滑移边界条件设置；

(3)由于Polyflow软件本身的设定，体积分数云图中若体积分数在0.5以上，则认为充满。

1.2 计算模型参数及工作原理

真空花板浇注工艺装置如图1所示。

工作原理：将混合好的可浇注药浆定量放入料斗中保温(温度50℃)，开启胶管阀，药浆按指定下料速度通过胶管阀进入真空度符合要求的燃烧室，将已除气的药浆通过真空压差和自重流入发动机燃烧室内壁和芯模之间的空隙内[8]。

计算模型在图1的基础上作了必要的简化设置，如图2所示。

图2 计算模型Fig.2 Calculation model

选取各个装置的参数如下：料斗内径90mm，花板直径90mm，孔简化为36个，孔的直径依次为3、5、7mm(实际中同一型号的花板孔径一致，为分析不同孔径的流速及挤出胀大效应，假设同一花板有不同孔径的分布)，浇注缸内径200mm，燃烧室内径100mm，燃烧室采用后翼、环型槽结构[9]，12个翼片。药柱芯孔最大处直径约40mm，前机口直径约15mm，后机口直径40mm，燃烧室总长200mm，直径100mm。

1.3 网格划分

本研究中计算域形状不规则，为了提高花板网格质量将整个模型分割为38个体，分别对其进行结构化网格划分。总网格数为442798个。网格划分情况如图3所示。

1.4 本构方程

研究表明[9-10]，固含量较高的推进剂药浆往往表现出非线性宾汉流体特征：当剪切应力低于屈服值时体系不流动，而高于屈服值时，剪切应力与剪切速率呈非线性幂律关系，且黏度随剪切速率增大而降低，即屈服假塑性流体[11]，亦称为Herschel-Bulkley塑性流体。

图3 网格划分Fig.3 Mesh division

本研究针对广义牛顿流体等温流动模型Herschel-Bulkley进行计算，形式如下[11]：

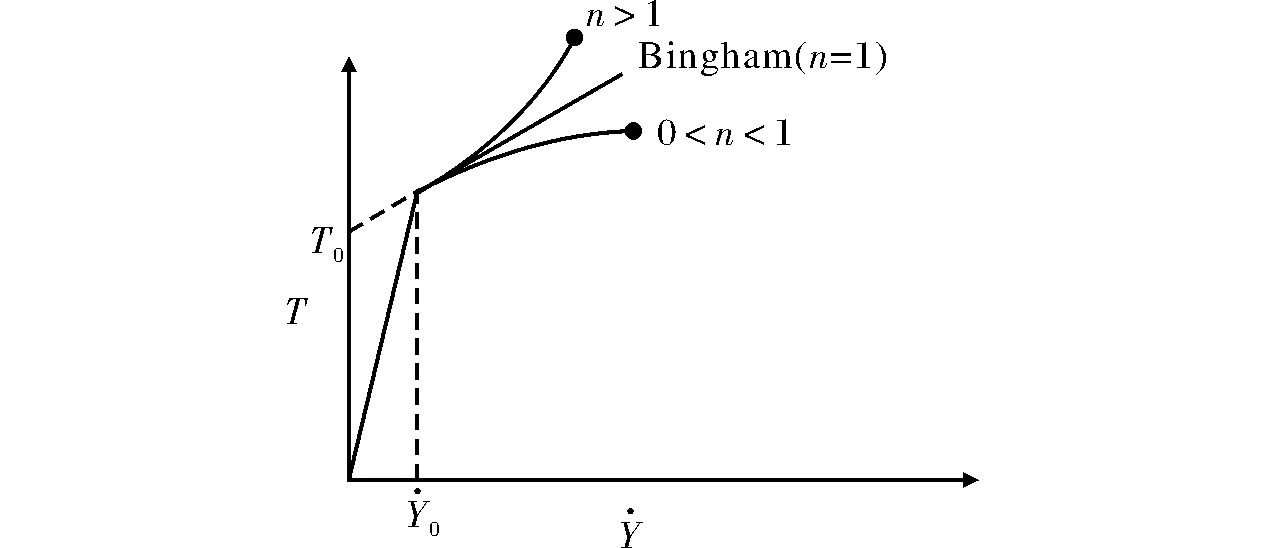
图4 广义宾汉流体的3类塑性流动Fig.4 Three types of plastic flow of generalized Bingham fluids

文献[11]表明，该固体质量分数为88%的四组元HTPB推进剂为典型的屈服假塑性流体，当施加的应力超过屈服应力后，体系发生流动，此时流动符合n<1的幂律定律。

1.5 边界条件

本研究在数值计算中涉及的边界条件有：流动入口边界条件、流动出口边界条件和壁面边界条件。

工程文件任务一的流动入口采用作用法向应力fn和切向应力fs,由于入口边界大气压强为0.1MPa，即fn=1.0×105，fs=0；流动出口边界采用作用法向速率vn和作用切向速率vs，且均为零；其余为壁面边界条件；由于选用有限元瞬态体积分数VOF(volume of fluid)模型，系统自动生成任务二Fluid Fraction Transport task，该任务边界条件入口采用Inflow边界条件，其余为壁面设置。

2 数值模拟结果与分析

2.1 花板孔径对药浆流动速度的影响

当黏弹性流体流经不同直径的花板孔时，其流动速率会有很大不同。圆截面不同孔径速度云图如图5所示。

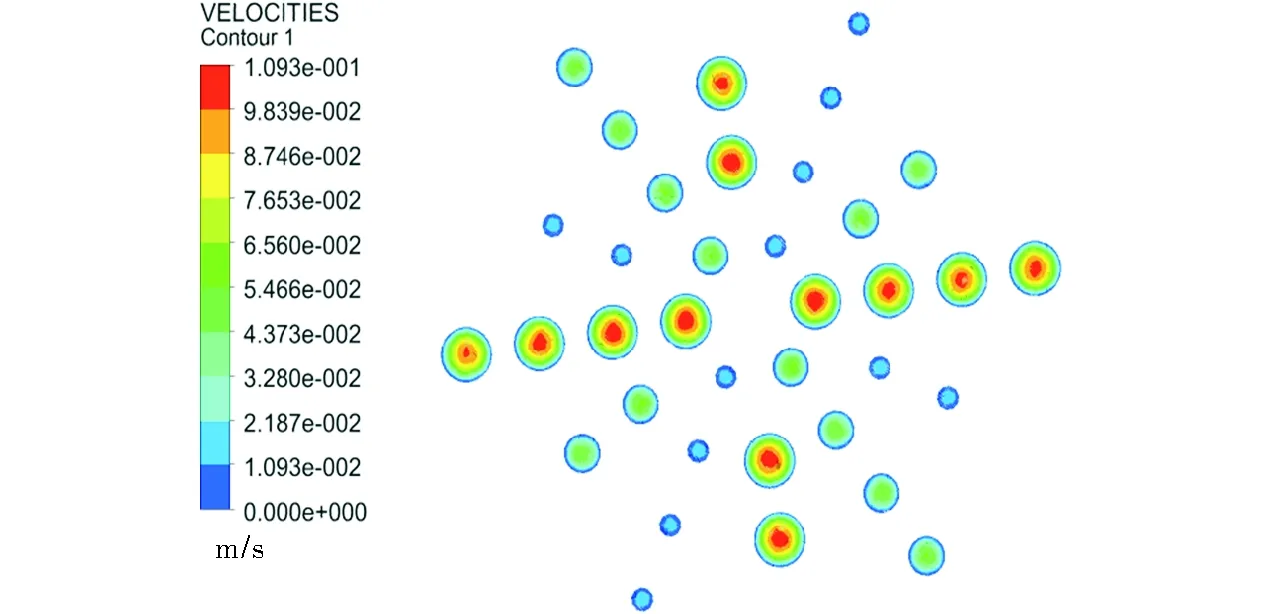
图5 圆截面不同孔径速度云图Fig.5 The cloud map with different orifice speeds in the circle section

由图5可以看出，孔径越大，流体的流速越大，且最大值出现在圆孔的中心轴线上：7mm孔径条件下，流速最大值约0.10m/s；5mm孔径流速的最大值约0.04m/s；3mm孔径流速最大值约为0.02m/s，这是由于孔径越大，流动阻力越小，质量流量越大导致流速越大，其次考虑到3种不同孔径，压强的相互竞争作用也会导致出现速度差异。

一般认为，与圆孔管壁处接触的流体层可视为静止的，因此圆孔管壁处流体流速接近于0[12]。

2.2 花板孔径挤出胀大效应分析

挤出胀大效应(BARUS效应)是非牛顿流体的典型流变特征[13]。图6为流体出口挤出截面，其大小用挤出胀大比(B=Dmax/D)表示。

由图6可以看出，由于花板厚度为5mm，所以3个不同孔径(3、5、7mm)的长径比依次为5∶3、5∶5、5∶7。通过Matlab软件编写程序拟合圆孔挤出截面直径，小圆(3mm)、中圆(5mm)、大圆(7mm)挤出截面直径拟合结果分别为3.1371、6.5546和10.08mm。即挤出胀大比依次为1.05、1.31和1.44。

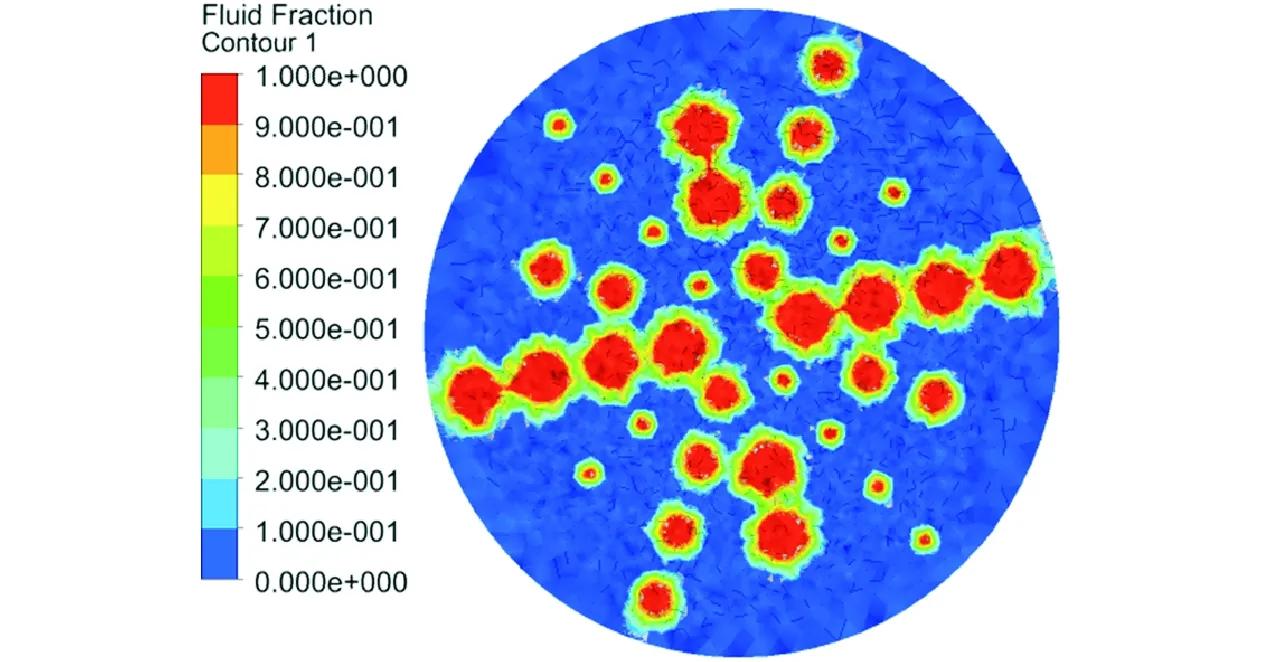
图6 圆孔挤出截面Fig.6 Export extrusion cross section

由此可见，花板孔径的长径比强烈影响挤出胀大比。挤出胀大比随孔径长径比减小而增大，当孔径长度一致时，孔径越大挤出胀大比越大。

2.3 黏度和剪切速率云图

HTPB丁羟四组元推进剂为典型的非线性屈服假塑性流体，其主要特征是在某一剪切速率范围内，黏度随剪切速率的增大而降低，即剪切稀变流体，从黏度和剪切速率云图中可以得到证实。

图7为某一YZ截面的黏度云图和剪切速率云图，图8为某一XY圆截面翼片位置药浆的黏度云图和剪切速率云图。所采用药浆初始黏度为400Pa·s。

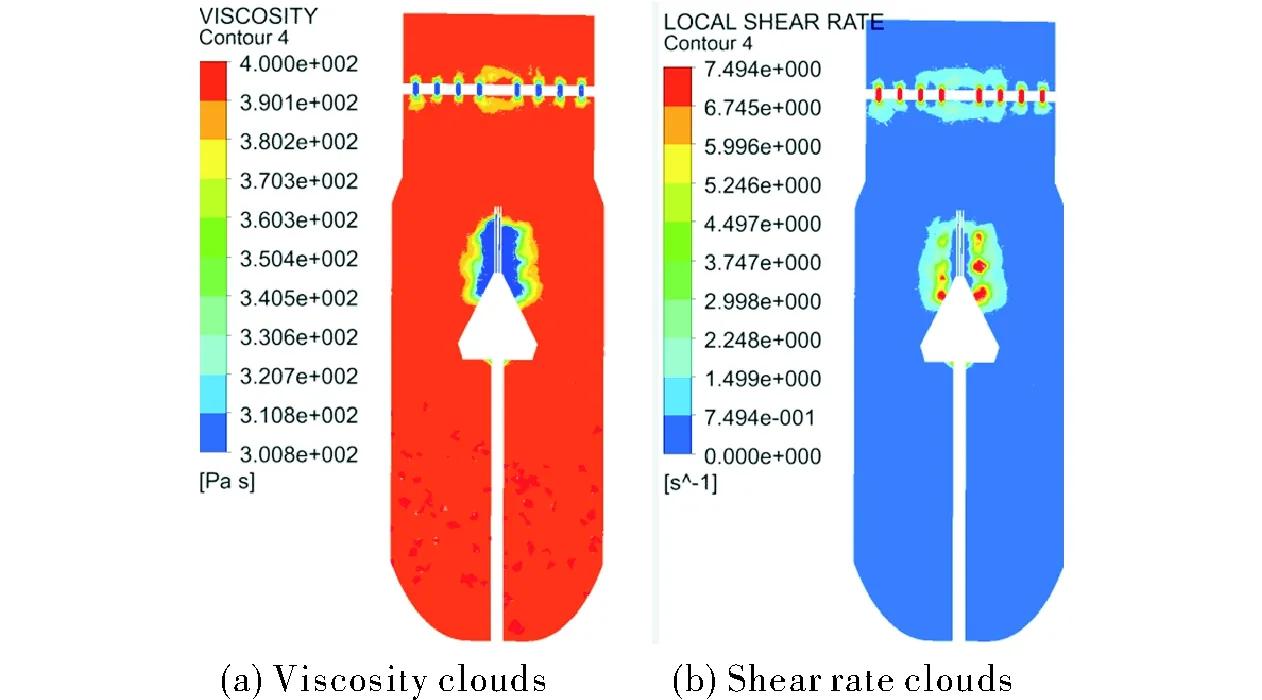
图7 某一YZ截面药浆的黏度云图和剪切速率云图Fig.7 The viscosity and shear rate clouds for a YZ section slurry

从图7和图8可以看出，药浆以较高的剪切速率流经花板和燃烧室翼片时，黏度降至最小值300Pa·s，当离开喷孔和翼片时，所受的剪切速率迅速衰减。产生以上结果的原因为：

(1) 流体流经花板不同孔径时，剪切应力和剪切速率大幅度提升，这是因为药浆从大面积料斗流道进入小截面圆孔时，流动状况发生巨大变化，入口区药浆会受到拉伸作用，出现明显的流线收敛现象，进而导致药浆不同层流之间的摩擦生热加剧，使得药浆连续相分子间热运动动能增大，从而提高流体的流动性，导致黏度下降[14]；

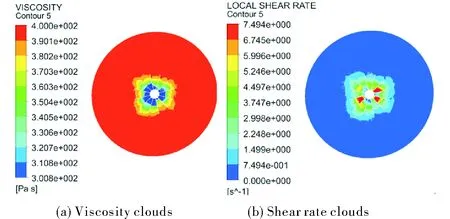
图8 某一XY圆截面翼片位置药浆的黏度云图、剪切速率云图和圆截面不同孔径速度云图Fig.8 The viscosity and shear rate cloud maps of the fin position for a certain XY circular section

(2) 流体流经燃烧室翼片时，固体推进剂连续相的黏合剂在翼片流动剪切作用下其高分子链段发生取向，这些高分子链时而相互缠绕，时而解开，从而分子之间的平衡力受到破坏，在高剪切速率下这种破坏难以在短时间内恢复，进而破坏了药浆内部黏滞结构，从而导致层流之间的运动黏滞度下降，黏度变小[15]。

此外，从计算模型的角度分析，所选用的本构方程为H-B方程，当流体超过临界剪切速率时，流动过程遵从假塑性流体幂律变化规律。除花板和翼片的其他位置的剪切应变速率很低，进一步证实药浆经真空花板浇注系统时，燃烧室中的流动是在低剪切应力和低剪切应变速率下的流动。

城市系统的模拟需要嵌入不确定的因素或者用户期望的因素，从而模拟出不确定性的城市系统或者用户所预期的城市形态.传统地理信息系统(GIS)在处理地理现象的时间过程上存在一定的局限性，而许多研究表明[1]，元胞自动机(CA)能更容易模拟各种现象随时空变化的动态性，这是因为CA非常适合模拟复杂系统.将GIS和CA结合起来，能够更好的模拟真实城市的发展，提高模拟的精度.

2.4 药浆流平性分析

将药浆离开花板喷口至充满燃烧室空间并淌平的过程称为药浆流平过程。 不同时刻药浆的体积分数云图如图9所示。

图9 不同时刻药浆的体积分数云图Fig.9 Volume fraction cloud chart of the slurry at different time

由图9可知，药浆在燃烧室均匀缓慢地从中间向四围展开，在真空压差和自重的综合作用力下逐渐充满燃烧室空间，这一过程与实际流动规律极为相似。药浆在4s左右通过花板流入燃烧室，整个过程流平性良好，直到t=46s时，燃烧室芯孔右侧出现一微小空洞，但其随着流动逐渐消失，直到燃烧室充满，孔洞的体积分数在0.5以下，可以忽略不计，基本充满。

本算例所采用药浆的屈服值为47.1Pa，从体积分数云图可以看出该药浆的流平性很好，表明推进剂在流平过程中屈服值越小流平性越好。

3 实验验证

本实验研究对象为某固体质量分数88%的端羟基聚丁二烯(HPTB)四组元推进剂，配方(质量分数)为：黏合剂，10.5%；高氯酸铵，60%；含能炸药，10%；金属粉末，18%；其他功能助剂，1.5%。密度为1.78×103kg/m3。

药浆在混合出料后约20min内通过落球黏度计进行黏度测定。推进剂药浆起始黏度值较低，为400Pa·s，模拟中初始黏度的取值与其对应。1h后药浆黏度升至759.12Pa·s，之后每1h测定一次，药浆黏度增长平稳，说明药浆整体性能良好。

3.1 模拟实验器浇注前准备

为尽可能真实地还原真空花板浇注实验，按照发动机燃烧室结构尺寸作如图10的模拟实验器。内径100mm，高200mm，体积为0.00157m3。与模拟选用的燃烧室尺寸一致。

图10 模拟实验器Fig.10 Simulation experimental device

该模拟实验器采用6mm厚度普通结构钢板焊接而成。装配前，首先用清理剂清理内表面，晾干后在内表面涂敷防黏剂，之后将试验器各个零件按照先底板后侧板的顺序进行装配，零部件之间加装密封垫。

3.2 模拟实验器浇注

浇注工装装配从下而上，依次为模拟实验器、套筒、花板、胶管阀和料斗等。花板采用Φ3mm×36mm规格，进行一次除气。

在浇注过程中，需有效控制胶管阀门开度，保证药浆下料速度，通过观察事先安装的线性速度传感器，显示流体经过3mm孔径时，速度为0.0158m/s，与模拟结果误差在允许范围内。记录四组元配方保温温度为50℃，记录浇注时U型压力机的读数为101000Pa，浇注缸内的余压为4000Pa，最终浇注历程总时长为2min。

实际浇注历程是模拟浇注时长的1.66倍，分析原因认为： (1)药浆非常黏稠，在流动过程中会在料斗和套筒等形成挂壁现象，挂壁越久越厚，而且在实际浇注过程中药浆会阻塞花板孔，延迟了总的浇注时间；(2)由于实验过程和数值模拟二者所选用花板规格的差异性，导致总浇注时间的差异。

综上，误差在一定的范围内，可以认定该模拟方法一定程度上正确反映了药浆的流动规律。

3.3 药柱质量检测

浇注工序结束后，将模拟实验器进行固化，并立即进行保温。检查其外表面无残药，并按照装配过程的逆顺序进行脱模。将药柱分解为Φ20mm×20mm的长条药柱，如图11所示。分解过程中，未发现药柱存在较大孔洞等质量问题。

图11 固体药柱的截面 Fig.11 Cross section of solid grain

4 结 论

(1)花板孔径越大，药浆流速越快。挤出胀大比随孔径长径比(L/D)减小而增大，当孔径长度一致时，孔径越大，挤出胀大比越大。

(2)推进剂药浆为典型的屈服假塑性流体，一定剪切速率范围内，黏度随剪切速率的增大而降低，且当流经花板和翼片时，流体剪切速率最大，黏度最低。药浆黏度和剪切速率在流动过程中发生变化。

(3)目前固体推进剂药浆的本构模型无法精确拟合，未来需补充实验数据，将本构模型精确化，如引入弹性项，建立线性黏弹性模型或微分形式和积分形式的非线性黏弹性模型，从而更好地描述药浆的流动状态。