临床研究中敏感性分析的统计思路与统计图表

谷鸿秋

在临床研究统计分析思路与统计图表系列的前三篇文章中[1-3]，我们将临床研究的统计分析思路归纳为描述基线信息、估计效应大小以及补充敏感性分析三部分，并对基线信息和效应估计的统计分析与图表做了详细论述。一篇临床研究文章在报告完基线信息和效应估计后，基本已是完整的分析结果。但临床研究统计分析结果的可靠性取绝于所用分析方法是否正确及方法背后的假定是否成立。因此，研究者通常会改用其它分析方法、改变假定条件再次分析数据，以考察结果是否改变及改变的程度，此即敏感性分析。敏感性分析结果是临床研究结果的重要部分，其分析思路和展现形式也值得临床研究者重视。本文将结合研究实例阐述敏感性分析所涉及的统计思路和统计图表。

1 敏感性分析的概念与内容

临床研究中，研究者在执行完效应估计后，通常还有这样的疑问：如果用不同的缺失数据处理方法，结果会改变多少；如果校正不同程度的协变量，效应差距有多大；如果用不同的标准定义结局变量，结论会偏移多少。诸如此类问题，都属于敏感性分析的范畴。关于敏感性分析，不同学者有不同的定义。Porta等编撰的流行病学词典给出的定义是：敏感性分析是一种通过改变方法、模型、未测量的变量值及假定来考察结果的改变程度，以确定评估方法的稳健性。敏感性分析的目的是识别那些最易被可疑的，无支持的假设影响的结果[4]。关于“稳健性”，国际人用药品注册技术协调会（International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use，ICH）在其统计学指导原则《ICH Harmonised Tripartite Guideline Statistical Principles Clinical Trails E9》中做过更详细的解释：所谓稳健性是指总体结论对分析所用的数据、假定及方法的各种局限的敏感性。稳健性意味着数据分析的假定和方法改变时，试验的治疗效应和主要结论本质上不受影响[5]。ICH E9的增补文件ICH E9（R1）给敏感性分析的定义是：针对同一估计目标，在偏离基本建模假设和有数据局限性时，基于不同的假设来探索主要估计量推断结果的稳健性而进行的一系列分析[6]。虽然定义表述有所差异，但本质上敏感性分析针对的是“如果主要输入或者假定改变”（what-if-the-key-inputs-orassumptions-changed），结果结论如何变化这类问题。

敏感性分析涉及的内容包罗万象，从数据的缺失值、离群值的不同处理策略，研究结局的不同定义，到不同的统计模型，以及相同统计模型里的不同层次的协变量校正，研究人群划分，亚组分析等均属于敏感性分析的范畴[7]。有学者专门总结过临床试验中常用的敏感性分析的场景[7,8]，其中大部分场景对观察性研究仍然适用。笔者结合文献及个人经验，归纳敏感性分析的适用场景为五大方面：数据、分析人群、变量定义、统计方法以及分布假定（表1）。

表1 敏感性分析的适用场景

2 敏感性分析的展现形式与案例分析

敏感性分析本质上是变化假定条件和统计方法再次执行统计分析，以回答效应估计是否改变。因此，敏感性分析结果的展现形式基本上与本系列第三篇文章论述的效应估计展现形式相同[3]，不过敏感性分析的结果常作为学术期刊文章的附表或附图，但也有将敏感性分析结果与主要分析结果整合在同一张效应估计的统计表格或者统计图中的情形。如Ekunday等利用“跟着指南走”（GWTG）数据评估是否使用急救医疗服务与卒中及时救治关系时，在主要分析结果中，剔除了NIHSS评分与医保类型缺失的观测，但在线附表中补充了纳入NIHSS评分与医保类型缺失的观测重新编码后的数据分析结果[9]。将敏感性分析结果与主要分析结果整合在一张效应估计统计表格中，常见于不同程度的协变量校正。如Sposato等利用PARADISE研究数据探讨卒中前与卒中后房颤与缺血性卒中复发的风险时，采用了三个统计模型，分别对年龄、性别、卒中严重程度以及出院时的抗凝治疗等协变量进行了不同程度的校正[10]。Smith等在利用GWTG数据分析卒中的不同分型与医疗质量时，也将未校正的结果、校正了医院特征的结果以及校正了医院和患者特征的结果统一呈现在一张效应估计表格中[11]，具体见图1。将敏感性分析的结果与主要分析结果整合在一张效应估计的统计图中，常见于带亚组分析的森林图。如CHANCE研究的主要结果与不同年龄组、性别、疾病史状况、血压分组、随机化时间以及用药时间等亚组分析结果便在一张森林图中呈现[12]，见图2。表1中不同场景下敏感性分析的具体案例，可参见Souza及Thabane等学者的描述[7,8]，本文不再一一赘述。

3 敏感性分析的统计方法与实现工具

敏感性分析中，针对数据和统计模型，会涉及一些特别的统计方法。本小节将对此做简要讨论。

3.1 离群值离群值（outlier）的检测，有两类方法：一是假设检验，二是标签法。假设检验法因数据分布假定的限制，以及遮蔽（masking）和覆没（swamping）问题突出，远不及标签法应用广泛。标签法通过数据是否超过某区间或违背某准则来判定是否为离群值。标准差法是最简单直白的标签法。当数据超过3倍标准差即为离群值。若先将数据进行Z值转换均数，sd为标准差），Z值的绝对值超过3则为离群值，此即Z值法。标准差法与Z值法均需计算均数和标准差，样本量较小时容易受极端值影响，因此便有了改良的Z值法。改良的Z值法计算时用中位数和绝对中位差（median absolute deviation，MAD）取代均数和标准差，其中MAD=median为样本的中位数。除此之外，还可借助箱线图判断。箱线图包含了中位数、低分位数（Q1）、高分位数（Q3）、低极值（Q1-1.5IQR）及高极值（Q3+1.5IQR）。离群值的定义为区间[Q1-3IQR，Q3+3IQR]以外的值，其它更多方法可见Seo的论述[13]。处理离群值，除了比较纳入、剔除标签法标记的离群值的分析结果外，还可采用稳健回归。稳健回归的基本思想是对不同数据点给予不同权重，小残差的大权重，大残差的小权重，以减小异常值对模型的影响，具体可参考Chen的论文[14]。

3.2 缺失值缺失值是临床研究中不可回避的问题。缺失值的处理策略，分为三大类：完全数据法、缺失数据标记法及缺失值插补法[15]。完全数据法即剔除含有缺失值的观测，仅用完全数据分析。完全数据法建议在样本量较大，缺失值比例较少（＜5%）时使用[16]。缺失数据标记法将分类变量值缺失的观测归为单独的一类，连续变量缺失值用固定数值（通常为0）插补，并额外增加一个变量标记是否缺失。缺失值插补法分为单值插补和多重插补（Multiple imputation）。常见的单值插补法包括均值（用于正态连续变量），中位数（偏态连续变量），众数（分类变量）插补，以及末次数据截转法、最佳数据截转法以及最差数据截转法。单值插补简单易操作，但会低估数据的变异，需谨慎应用。多重插补是依据数据集中其它变量的分布对缺失数据进行多次插补形成多个完整的数据集，而后采用标准的统计方法分析每个完整数据集，最后再汇总多个数据集的分析结果。多重插补时依据缺失的模式（单调或任意）以及所填补变量的类型（连续变量、二分类或有序变量及无序多分类变量），可采用不同插补方法，包括线性回归、预测均数匹配、倾向性评分、Logistic回归、判别函数、马尔科夫链蒙特卡洛以及全条件定义等。R平台的多个统计软件包（Amelia[17]、mice[18]及mi[19]）、SAS软件的PROC MI以及PROC MIANALYZE过程均可实现多重插补的操作[20]。更多关于多重插补的讨论可见Sterne的文章[21]。

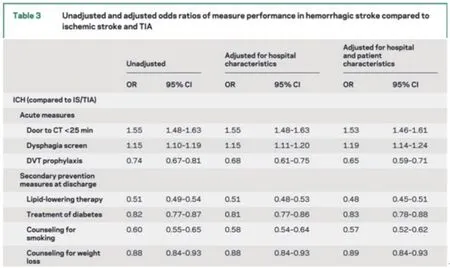
图1 同一模型中不同层级的协变量校正

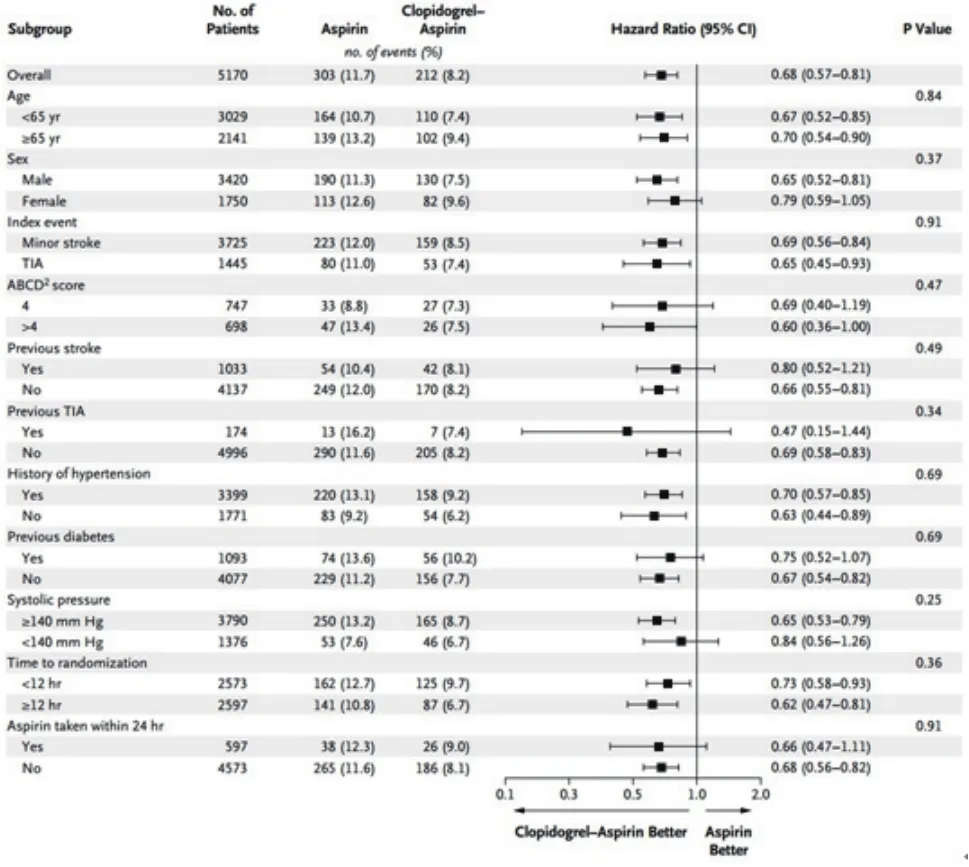
图2 CHANCE研究亚组分析森林图

3.3 群组效应常规的统计模型均要求观测间互相独立，若观测间不独立，则需处理其相关性。同一医生的患者、同一家医院的患者或同一社区的患者相比不同医生、不同医院或不同社区的患者有更多相似性，因此在统计模型中，常将其归为一个群组，以控制群组效应。同一个患者不同时点的重复测量数据也属此类。控制群组效应，常用广义估计方程（GEE）[22]或混合效应模型[23]。R平台的geepack、lme4软件包可分别实现GEE和混合效应模型[24,25]。SAS平台可借助PROC GENMOD或PROC GEE过程实现GEE[26]，PROC MIXED、PROC GLIMMIX以及PROC NLMIXED过程可实现不同类型结局资料的混合效应模型，具体参见SAS帮助文档[27]。

3.4 竞争风险对于生存数据，当有多个结局事件，且某结局事件的发生会影响甚至阻止其它结局事件的发生，就会存在竞争风险[28]。如研究者关注卒中复发，一旦死亡提前发生，则无法观察到卒中复发结局。对于竞争风险，常见的处理策略有：（1）将多个事件打包整合成一个联合事件，采用Kaplan-Meier估计生存率[29]，Log-rank检验比较组间差别，Cox比例风险模型估计风险比[30]；（2）将其它事件视为删失，分别对每个事件估计累积发生率（CIF），并采用原因别风险函数（cause-specific hazard function）估计风险比[31]；（3）将发生其它事件的研究对象仍纳入风险集，估计关注事件的CIF，并采用次分布风险函数（sub-distribution hazard function）估计风险比，此即Fine-Gray模型[32]。将事件打包成联合事件，存在两个缺陷：一是联合事件不一定具有临床意义，可解释性差；二是无法精细分析各成分事件，造成信息损失。原因是风险模型和次分布风险模型各有其独特的解释：前者更适合回答病因学问题，反应协变量对无事件风险集人群的终点事件发生率的相对作用；后者更适用估计疾病风险与预后，体现协变量对无关注事件风险集人群的终点事件发生率的绝对作用[33-36]。R平台软件包cmprisk的cuminc()、 survival的coxph()、以及cmprisk的crr()函数，SAS平台PROC PHREG过程的PLOTS=CIF过程选项、MODEL语句的EVENT(COX)=选项（需要SAS/STAT 14.3版本）、及EVENT=选项可分别实现CIF的计算，原因别风险函数估计及次分布风险函数估计[37,38]。更多关于竞争风险的分析可见Wolbers及Austin的文章[39,40]。

4 敏感性分析的结果解读与报告

敏感性分析的目的不是筛选最有利的结果，而是考察结论的稳定性。因此，论文中应报告所有的敏感性分析结果。当敏感性分析结果与主要分析结果一致时，可将其作为附表或附图，正文中简要说明当前的结论是稳健的即可。当敏感性分析结果与主要分析结果不一致时，说明主要分析的结果并不稳健，建议在结果部分直接呈现敏感性分析结果，以引起读者的注意与思考，并在讨论部分分析、解释可能的原因，如有需要，还应进行模拟研究。如何规范的执行和报告敏感性分析，目前并未统一规范。普遍认同的是，计划的敏感性分析应在研究方案中提前申明，事后的敏感性分析也应在统计分析计划中详细说明，并阐述缘由和依据。

本文是临床研究统计分析思路与统计图表系列文章的终末篇。至此，从总论到基线信息、再到效应估计，最后到敏感性分析，我们从方法学上构建了一条临床研究统计分析思路的完整逻辑链条，后续还将对预测模型、诊断研究等专题做特别讨论，以期为临床研究同仁提供借鉴。