基于改进遗传算法的门式刚架截面优化
2018-11-08李彬汪小平张柳春朱南海
李彬, 汪小平, 张柳春, 朱南海
(江西理工大学建筑与测绘工程学院,江西 赣州341000)
0 引 言
钢结构建筑具有施工速度快、施工扬尘少、可循环利用和节能环保等特点,在我国工业建筑中有较广泛的应用,特别是门式刚架在轻钢厂房中的应用.门式刚架作为一种传统结构,历经近百年的发展,已经形成一套设计、制作及施工相对完整的体系[1-3].传统钢结构结构设计,包括门式刚架设计,一般先由设计人员根据设计经验,初步选定构件截面类型和截面尺寸,然后进行承载力、稳定性和变形验算,验算通过后即完成设计,一般并不进行方案比选和优化.但是,由于设计人员的设计水平和设计经验的差距,同一工程项目不同人员进行设计时,其结构用钢量可能产生巨大差异.有的设计单位用钢量大,造价偏高,造成不必要的资源浪费.因此,对门式刚架采用优化算法进行全局搜索,从而得出最优设计方案的过程对于门式刚架结构的优化设计有着十分重要的意义.
门式刚架主体结构由钢柱钢梁组成,因此其优化也主要从减少这两种构件的总重量来实现.通过优化钢柱钢梁的截面尺寸,从而完成门式刚架的结构优化设计.目前,国内外对门式刚架的截面优化主要集中在三个方面:一是对构件的尺寸及形状采用拓扑优化,二是采用枚举法实现多个方案间比选优化,三是采用搜索算法对截面参数进行优化选择[4-9].其中,枚举法需要列出所有可行解集合,理论上存在无数种可能,需要花费大量时间来完成,甚至可能得不到最优可行解;拓扑优化则是通过设置合理去除率并进行应力计算完成构件重量的优化,更多是对构件形状的优化,对构件截面尺寸的优化难以实现;搜索算法可以通过设置一个可行域的子集并在其中搜索,从求解出问题的最优解或者近似最优解.遗传算法由美国教授J.Holland在1975年受到生物进化论的启发提出[10-11],相较于传统搜索算法,通过模拟自然界的自然选择和进化过程,具有搜索速度快能自动收敛的特点,被广泛的运用于优化计算体系中,如今更是作为群智能算法运用于各个行业.文中利用遗传算法搜索速度快、能自动收敛的特点,将钢材截面类型和截面尺寸参数离散化为种群的可行解集,通过选择、交叉以及变异等一系列遗传操作过程,完成钢材截面选型和截面尺寸的确定.
1 改进遗传算法在门式刚架截面优化中的应用
1.1 问题的提出
如图1所示的门式刚架结构,梁柱构件可采用型钢或者焊接组合钢,截面类型(OTHI)可以为T型、H型、工字型等,每一种截面类型可以选取不同规格,例如 HW250×250、HM300×200、HN350×150 等上百种截面尺寸中进行选取.设计目的是在选定的型钢集合以及焊接钢材的范围内,在满足安全要求及使用要求的条件下,得到结构总用钢量最小的设计方案.
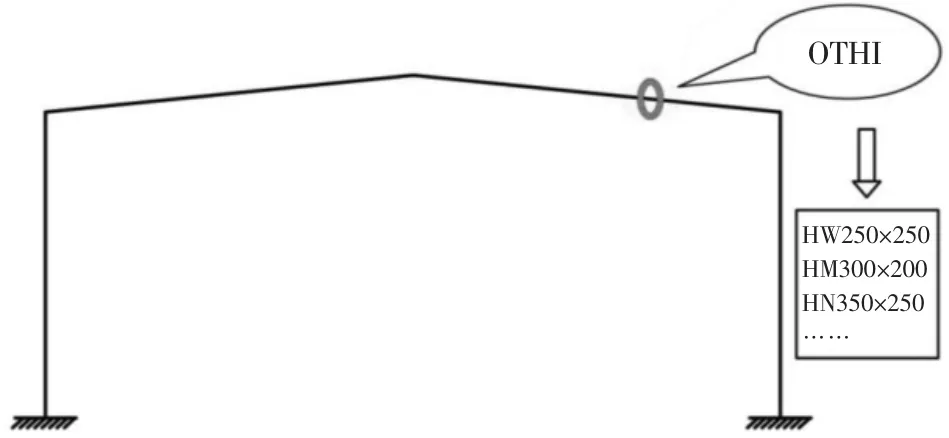
图1 门式刚架示意
1.2 改进的遗传算法
传统遗传算法一般采用单一编码方式,不能处理不同情况下的多种规则状况的优化搜索.针对这一问题,文中采用十进制与二进制混合编码,同时在交叉和变异过程中保护某些种群个体特殊性质和参数,形成多层次遗传算法,进行最优截面搜索[12].
1.2.1 初始种群及编码
在遗传算法中,初始种群化代表初始可行解的数量,其经验数值为20~100.而编码过程,则是对初始可行解的参数在一定范围内进行随机生成.文中模型采用的是一维、变长、十进制结合二进制混合编码,模型编码结构如式(1)所示:
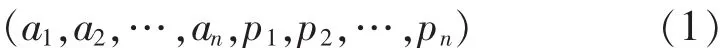
式(1),中(a1,a2,…,an) 是钢材种类编码串,采用十进制编码,ai长度为1,可表示一种钢材类型编码(例如:a1可以代表型钢工字钢,a2则可以代表焊接工字钢). (a1,a2,…,an)的总长度则根据模型所选取的种类来确定,可以表示n种钢材类型.
(p1,p2,…,pn)是钢材截面参数编码串,采用二进制编码,pi长度则根据所选取的截面参数范围及求解精度确定 (例如:p1可以表示为焊接工字钢的高度,p2则可以表示为焊接工字钢翼缘宽度),每个参数在编码前应进行离散化处理.(p1,p2,…,pn)的总长度则根据所需截面参数的数量来确定,可以表示n种截面参数.
1.2.2 交叉和变异保护策略
在遗传算法的运行过程中,新一代种群主要通过老一代种群的染色体交叉和变异过程产生,由于其具有随机性,会产生完全不同的编码结构.文中所用模型采用的是一维、变长、十进制结合二进制混合编码,若采用传统的交叉和变异过程,会产生混乱的编码结构,导致解码过程复杂,不能进行统一解码,增加程序计算复杂程度.因此,为了保证种群个体的特殊属性以及参数,文中采用保护个体部分参数的办法来对遗传算法的交叉和变异过程进行改变.具体操作方法与过程是:
将完成遗传算法选择过程的老一代种群的染色体分为两个部分,第一部分为钢材种类编码串,第二部分为钢材截面参数编码串,两部同时进行交叉,并且规定第二部分若进行交叉则第一部分编码位置互相交换,反之亦然.完成交叉过程之后,进行变异过程,为了保持种群个体钢材种类编码串的特殊属性,变异过程仅对钢材截面参数编码串进行.
经过上述方法的交叉和变异过程,产生了新种群,也保证了种群个体的特殊属性.同时,经过交叉和变异的保护策略,可以减少编码过程中出现杂乱无章的情况出现,从而减少遗传算法的运算复杂程度,降低计算时间.
1.3 门式刚架内力计算
门式刚架的内力计算,目前设计过程中一般采用电算进行,其基本原理为有限元法.因矩阵位移法与有限元法同出一源,更适合计算机编程计算[13],因此,文中对门式刚架的内力计算,通过遗传算法初始种群过程中产生的截面参数带入矩阵位移法完成.
矩阵位移法一般通过单元编码以及节点编码开始.随后对梁单元进行模拟,未进行坐标转换之前,梁单元的单元刚度矩阵,如式(2)所示:

其中:E为钢的弹性模量;l为构件长度;A和I分别为构件截面面积和截面惯性矩,可以通过对遗传算法中截面参数编码串进行解码,得到构件钢材的高度h、翼缘宽度b、翼缘宽度t以及腹板厚度tw,再进一步计算求解得出A和I.
将各个构件的单元刚度矩阵求解完成后,采用单元集成法,形成结构整体刚度矩阵K.同时,采用相同方法,求解出整体结构的等效结点荷载向量P.根据整体刚度矩阵和等效结点荷载向量之间的关系,如式(3)所示,求解结点位移向量.进而通过式(4)求解出构件的杆端内力向量.


式(4)中,杆端内力向量包括杆两端的轴力、剪力以及弯矩.
1.4 适应度函数及约束条件
假设门式刚架有 C1,C2,…,Cn共 n 个构件,则每一构件的截面面积A1,A2,…,An可以通过编码随机获得截面参数进行求解.再根据钢的密度ρ,构件的长度li,可以求解出整个门式刚架的结构总重量如式(5)所示:

则目标函数及约束条件为:
find:A=[A1,A2,…,An],i=1,2,…,n
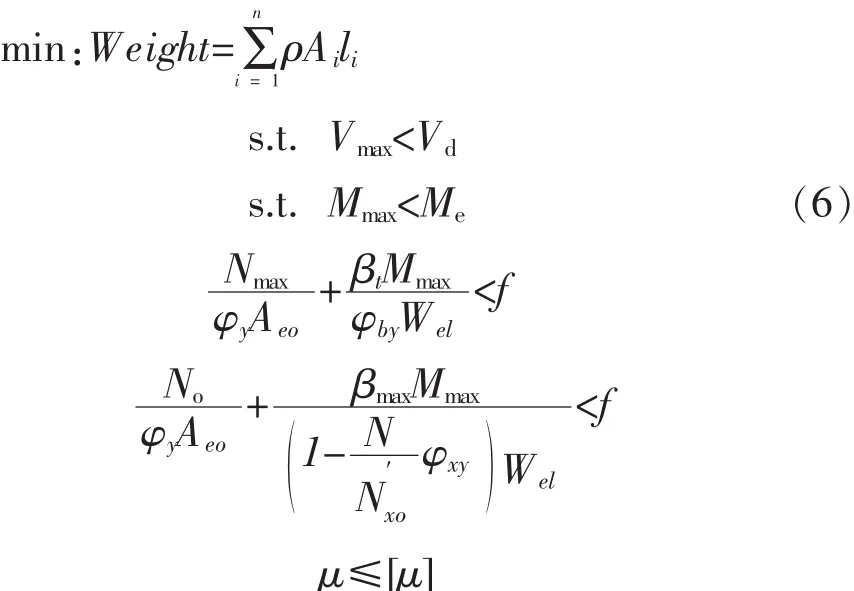
对于式(6)中的约束条件并不是所有遗传算法产生的构件类型都满足,因此对于不满足约束条件的构件,应对其进行惩罚(额外增加重量),从而使得进行种群选择过程中能被淘汰.故遗传算法的适应函数建立,如式(7)所示:
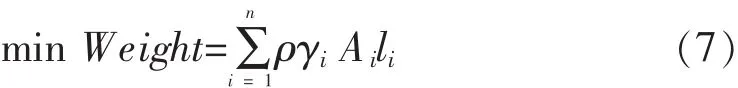
其中:γi表示每一个构件的惩罚因子.
通过对遗传算法过程中编码、交叉和变异进行改进,采用矩阵位移法计算结构内力,将门式刚架的构件宽厚比验算、强度验算、剪切验算、整体稳定性验算以及柱顶位移验算作为约束条件,从而完成整个门式刚架设计的截面优化研究.整个计算优化过程的流程如图2所示.
2 算例分析与讨论
2.1 基本资料
某单跨双坡门式刚架,,跨度12 m,柱高5 m,屋面坡度1/10,刚架立面图如图3所示.抗震设防烈度6度,基本风压值为0.4 kN/m2.屋面及墙面为夹芯彩钢板;檩条墙梁为薄壁卷边C型钢,钢材采用Q235钢.
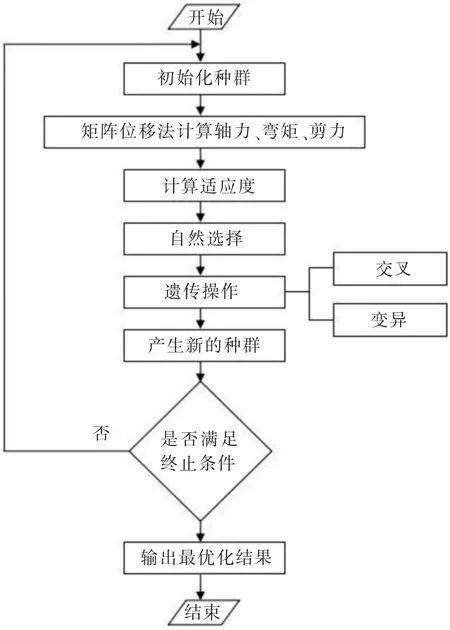
图2 优化算法流程
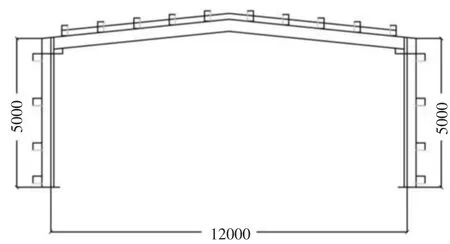
图3 门式刚架立面图(单位:mm)
2.2 计算过程
2.2.1 钢材类型及截面选取
针对所选取的单跨双坡门式刚架,选取了10种截面类型,即:工字型钢、窄翼缘H型钢、中翼缘H型钢、宽翼缘H型钢、窄翼缘T型钢、中翼缘T型钢、宽翼缘T型钢、焊接工字钢、焊接H型钢以及焊接T型钢.
其中,型钢部分选取国内常用的型钢,焊接钢部分则选取截面参数范围,选取结果如表1所示.
表1中型钢和焊接钢可选取种类数量差异过大,由于型钢只需要确定任意一个参数,即可确定其余所有参数,故钢材类型选取种类较少;而焊接钢的四个参数进行组合可得到新的截面类型(截面高度和翼缘宽度以10为模量进行改变,腹板厚度和翼缘厚度以0.5为模量进行改变),故焊接钢的截面组合类型更多.
2.2.2 改进遗传算法
种群控制性参数:算例选取种群规模为100,遗传代数为2500代.
编码:采用一维、变长、十进制结合二进制混合编码,型钢染色体长度为21或25,焊接钢染色体长度为89.
选择:将解码完成的参数,带入适应度计算函数,依照总重量最小原则,对整个种群采用轮盘赌的方式进行选择,保留优秀个体或者小几率保留不优秀个体.
交叉和变异:算例采用保留个体特殊属性策略来完成交叉和变异过程,对十进制编码部分和二进制编码部分分别交叉和变异.交叉过程采用单点交叉完成,其交叉概率为0.8,而变异过程采用随机变异完成,单点变异概率为0.01.
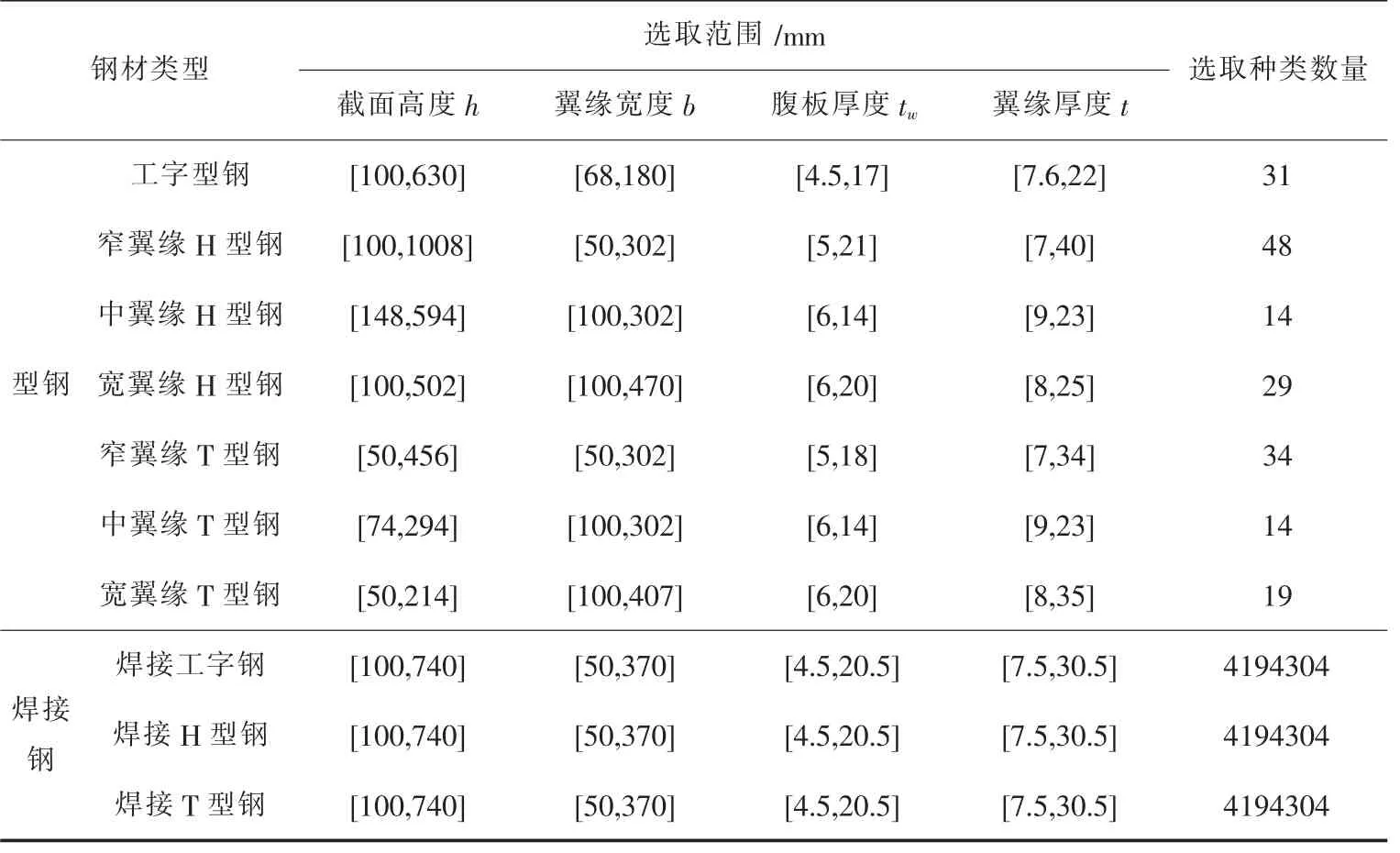
表1 钢材选取类型
2.2.3 矩阵位移法计算内力
根据门式刚架设计资料,其基本风压为0.4 kN/m2,计算出恒荷载和活荷载,得到门式刚架荷载图如图4所示.再将其荷载值以及解码所得截面参数,带入矩阵位移法中,可以得到门式刚架结构内力,见表2.
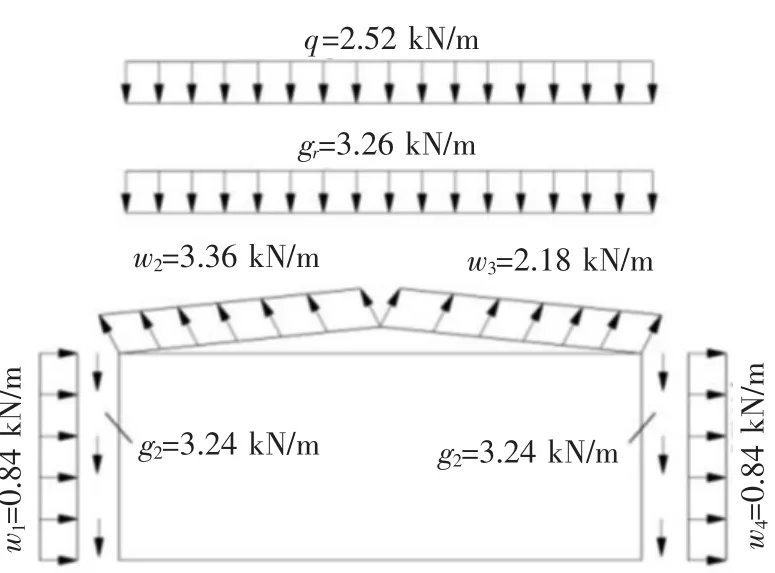
图4 门式刚架荷载
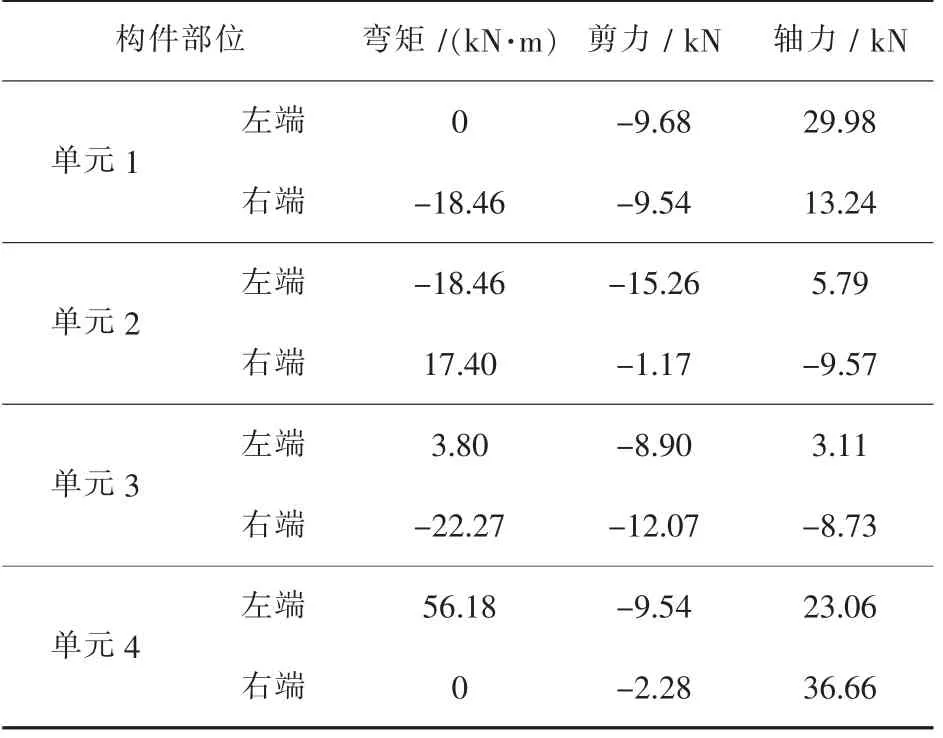
表2 门式刚架结构内力
2.3 计算结果
图5表示改进遗传算法从第1代进化至第2500代进化过程中,门式刚架总重量不断被优化,在满足约束条件下,每一代门式刚架总重量最小的情况.从图5可知,随着不断进化,门式刚架总重量一开始呈现出局部上升,随之开始不断递减,最终趋于平稳.其最适应个体变化,说明改进遗传算法在进化中不断淘汰总重量高的个体,但由于选择和变异过程具有随机性,故会出现保留总重量高的个体.随着进化的不断进行,最终只有总重量低的个体被保留,经过2500代进化,门式刚架总重量最轻个体出现在第53代,其最佳个体的截面参数,如表3所示.
将同一算例的文中计算机电算结果与文献[14]手算结果进行比较,其在一榀门式刚架设计时,能优化5%的结构重量.
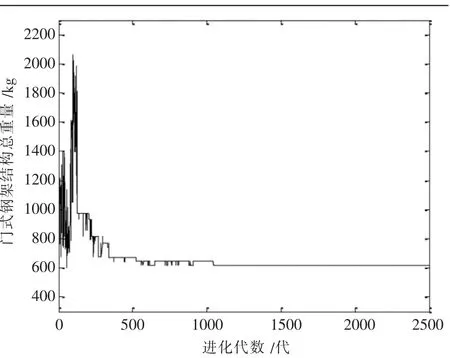
图5 改进遗传算法计算结果
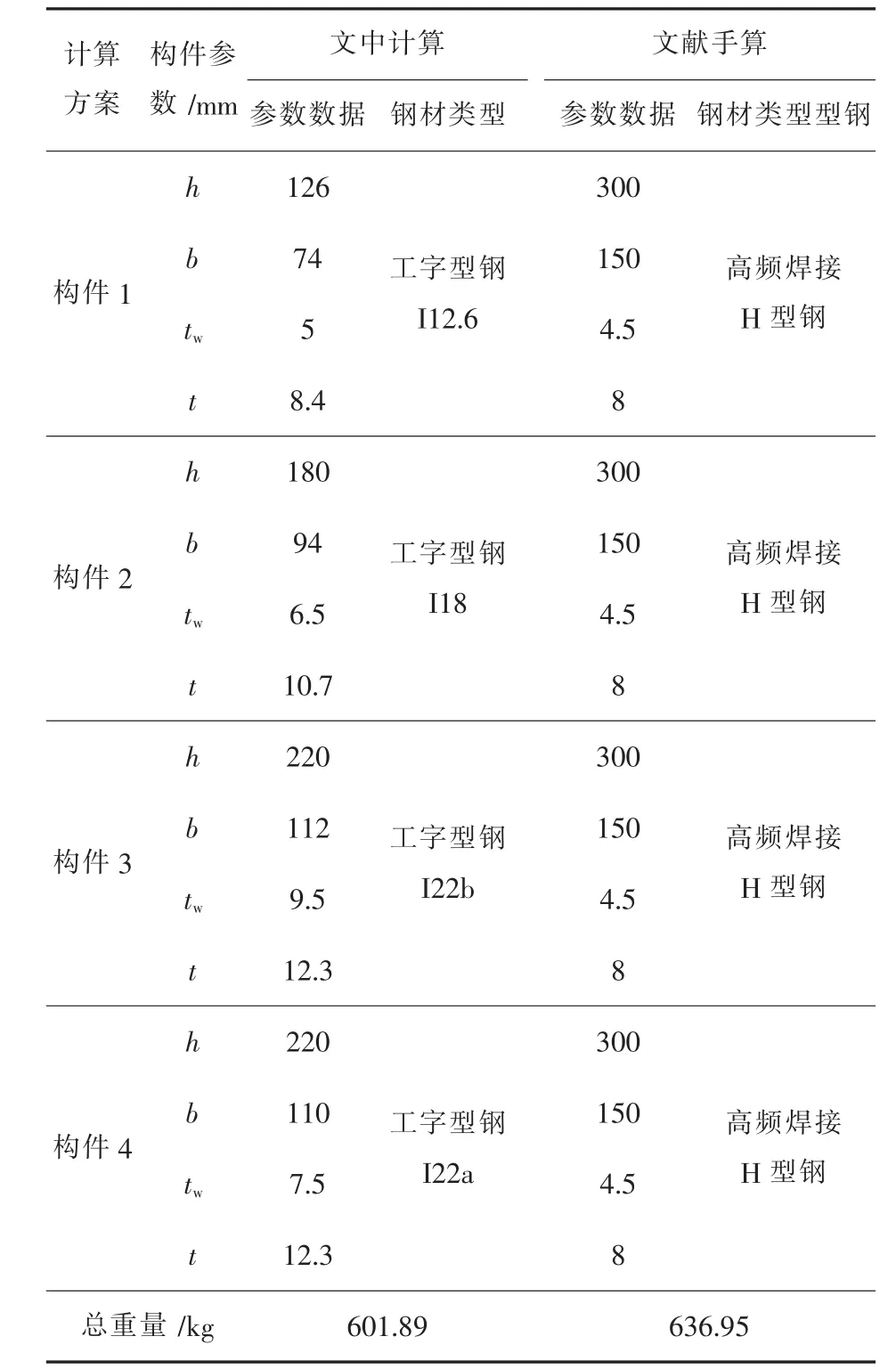
表3 改进遗传算法优化结果比较
3 结 论
1)门式刚架的截面优化是离散变量的优化问题,而且变量参数多,很难用传统方法进行优化计算.针对这一问题,文中采用改进遗传算法进行优化计算,可以有效处理传统优化算法难以处理的多变量参数优化问题,从而完成全局最优变量搜索.
2)门式刚架的截面优化,包括型钢和焊接钢等多种类型钢材,同时还有众多截面参数的类型,传统遗传算法难以实现优化搜索.文中采用一维、变长、十进制结合二进制混合编码的改进遗传算法,有效实现了优化搜索,且有效率较高.
3)采用个体特殊属性保护策略,将个体的十进制编码部分和二进制编码部分分别进行交叉和变异,从而保证个体编码过程中特殊属性.通过上述方法,进行遗传算法的遗传操作过程,实际上也消除了程序编码出现混乱的可能性,从而进一步保证程序计算运行的正确性,使得整个优化过程在高效率性及正确性的基础上完成.
4)通过实际算例优化研究,并与文献中手算结果进行比较,得出所采用的的算法模型可以降低结构重量的5%,为门式刚架截面选型和截面尺寸选取提供了一种有效可靠的优化设计方法.
