创设有效问题情境 培 养数学核心素养—以《正弦定理(第一课时)》的证明为例

江苏省姜堰第二中学(225500) 张新志

2017版《普通高中数学课程标准》中明确指出:“情境创设和问题设计要有利于发展数学学科核心素养,基于数学学科核心素养的教学活动应该把握数学的本质,创设合适的问题情境、提出合适的数学问题,引发学生思考和交流,形成和发展数学学科核心素养.教学情境是多样性的,每种情境可以分为熟悉的、关联的、综合的.数学学科核心素养在学生与情境、问题的有效互动中得到提升.也就是说在教学活动中,应结合教学任务设计有效的问题情境,促进学生数学核心素养的形成和发展”.

人教社章建跃老师指出,一节好课的基础是老师要“理解数学”、“理解学生”、“理解教学”、“理解技术”.数学育人的载体是数学内容和内容所反映的思想方法,假若老师对数学内容理解不到位,一切也都是空谈;理解学生的核心是理解学生的数学认知规律和情感发展规律,也是“以学定教”的前提;理解教学的核心就是对数学教学规律的认识和教学机智的运用策略水平;理解技术就是善于利用信息技术手段辅助于教学.

2017版《普通高中数学课程标准》,新增了学科核心素养、课程结构、学业质量三个重要的部分,同时课程标准还围绕核心素养和教学评价给予了相关案例,帮助高中数学老师在教学实践过程中更好地落实数学核心素养.核心指导思想是以学生发展为本,促进学生在不同的学习阶段数学核心素养水平的达成.文2从MPCK的角度认为问题情境的引入应该从学生熟悉的直角三角形边和角之间的关系入手.文3认为从日常的测量问题引入,创设问题情境.本节课的重点是基于培养学生的数学核心素养,创设开放的、发挥学生主体意识的问题情境,让学生在最近发展区中去寻求三角形的边角关系,教师着眼于课堂教学,让问题情境变的更有效！

基于此,在市级教学观摩课,课题内容是苏教版数学必修五1.1正弦定理(第一课时),教学设计时改变了问题情境的引入方式,力求让问题情境更有效,基于学生已有的知识,通过问题的解决,引发学生对任意三角形边角关系的探究.

1.教学实录

1.1 创设有效情境,指向问题解决

问题1如图1,河的两岸有两座灯塔分别为A和B,现在不过河的情况下,要测得A和B之间的距离,如果我们有足够长的卷尺和能够测量角的测角仪.你能测量出AB之间的距离吗?

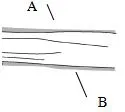
图1

教学备注情境教学不仅仅要发挥学生的主体性,还要激发学生的兴趣,本问题是从日常学生熟悉的测量问题入手,创设情境使学生产生学习数学的渴望.问题提出后,学生积极性很高,连平时不愿意回答问题的学生也跃跃欲试.

生1:可以沿垂直于AB的方向行走到C点,用测角仪测出角∠ACB=45°,A和B之间的距离就是线段BC的长！

师:很好,我们可以利用卷尺和测角仪求出AB的长度.

问题2如图2,如果BC之间有座山怎么办呢?

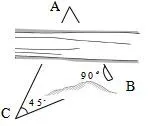
图2

教学备注“数学是思维的体操.”教学是数学思维活动的教学,是思维过程的教学,思维活动匮乏的数学课是不成功的,往左侧作等腰直角三角形的办法是行不通了,往右是河也行不通！问题2的设计充分调动学生学习的积极性和主动性,很好的激发了学生的思维,从而提高解决数学问题的能力.

生2:可以从B点沿垂直于AB的方向往左或右行走到C,测出BC的长,再测出∠ACB的大小,利用直角三角形可以求出AB之间的距离.

问题3如果规定不能沿着垂直于AB的方向行走呢?

生3:可以调整行走方向！

师:那谁能说一下调整行走方向以后,如何求AB之间的距离呢?

生 4:如图 3,∠ABC=120°沿的方向行走至点C,使得∠BCA=45°,利用卷尺能测出BC的长.

图3

师:那现在也不知道BA之间的距离啊！

生5:可以从B点向AC作垂线BD,在直角三角形BCD中能求出BD的长,又因为∠BAC=15°,所以在直角三角形ABD中能求出AB的长.

师:如果∠ACB=α,∠ABC=β,BC=a,如何求AB的长呢?

学生都异常兴奋,大声齐喊:作垂直转化成直角三角形！

教学备注苏霍姆林斯基说过:“在人的心头深处有一种根深蒂固的需要,这就是希望感到自己是一个发现者、研究者、探索者”.笔者所创设“问题情境”正是为了满足学生这一需求.激发学生在学习兴趣的基础上组织学生高度地参与数学思考活动.

师:对于解三角形问题,如果我们每次都是作垂线转化成直角三角形是不是很麻烦啊?

生:齐声喊“是”.(此时班级气氛异常活跃)

师:我们知道三角形有六个元素,三条边和三个角,三角形的边和角之间到底有什么关系呢?

(此时教师板书“解三角形”)

师:研究未知我们往往都是先从熟知开始,同学们想一想,我们首先要研究哪种三角形呢?

生6:直角三角形.

1.2 以旧知为起点,特例发现新知

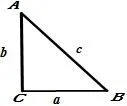
图4

问题4直角三角形的边与角之间存在怎样的关系?

生7:应该也成立吧.

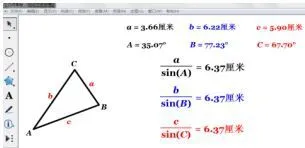
图5

教学备注学生从未知到熟知的认知过程是一步一步走进的,需要搭建一个一个台阶,从特殊的三角形开始探索,启发学生思考所学习过的直角三角形中的边角关系,体现了从特殊到一般的的数学思想方法.又引导学生猜想,在一般的三角形中,比值是否也相等?猜想验证是一种重要的数学思想方法,正如荷兰数学教育家弗赖登塔尔所说“真正的数学家——常常凭借数学的直觉思维做出各种猜想,然后加以证实.”,华罗庚说:“数缺形少直观,形缺数难入微.”,通过几何画板的演示给了学生创造一个实际“操作”几何图形的环境.让学生通过任意拖动点C、观察比值、猜测并验证结论,从而更有助于学生理解和证明.

1.3 归纳概括猜想,证明得出定理

师:上述的探索过程所得的结论,只是我们通过猜想验证得到的结果,我们如何证明呢?前面探索过程对我们有没有启发?

生8:由问题情境,我们可以采用分类讨论的思想,可以分为直角三角形、锐角三角形、钝角三角形三类分别来证明,类似于问题情境的解决思路,利用作高线最终转化为直角三角形中的边角关系来证明.

图6

(学生小组合作,把证明过程写在纸上,利用展示台进行班级展示.)

证明(1)若∠C为直角,我们已经证明结论成立.

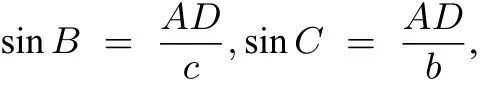
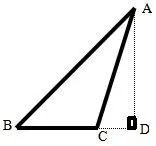
图7

教学备注波利亚说:“为了得到一个方程,我们必须把同一个量以两种不同的方法表示出来,即将一个量算两次,从而建立相等关系.”,这种证法就是运用算两次的方法,找出了三角形中边和角之间的关系,结合学生的认知特点,选择小组合作各组展示的教学方式,通过作高线的方法,把陌生转化为熟悉,这种证法渗透了转化、数形结合、分类讨论等重要思想,通过教学让学生理解正弦定理的内涵,让学生感受“观察—猜想—证明”的科学研究问题的思路.

师:正弦定理研究的是任意三角形的边角关系,观察式子结构,里面有边及其边的夹角,我们在前面学习了平面向量,向量是解决数学问题的有力工具,那么同学们能否用向量的知识证明正弦定理?

师:怎样将此向量关系转化为数量关系?

生9:等式两边平方.

生11:要想办法将向量关系转化为数量关系.

生12:向量的数量积可以将向量关系转化为数量关系,同时还要想办法将有三个向量的关系式转化为两个向量或数值的关系式.特别地当两个向量垂直时,利用点乘法能得到数量积为0,所以优先考虑选取相互垂直的向量.

师:很好,如果两边平方,同学们在一不小心的情况下就证明出了余弦定理,那如何转化?

图8

教学备注向量融长度和角度于一体,学生虽然学习过向量知识,但以向量为载体证明正弦定理还是比较困难的.在引导学生利用向量去证明正弦定理,无论是基于学生个性差异的视角或基于动机激发的视角,都归结于在课堂活动中如何激发学生参与的动力,在向量往数量转化的方法中学生的思路比较多,要肯定学生的想法,不能为了完成证明而变成教师的独角戏,而是师生之间的大合唱.

2.教学反思

数学的核心素养是数学课程目标的集中体现,是数学教与学过程中应当特别关注的重点.本节课的设计使学生经历了“观察——猜想——验证——证明”的思维历程,让学生学会研究数学问题的基本思想方法.让学生从有效的问题情境中不断地去探索问题的解决、定理内涵的挖掘,从知识上加深对概念、定理的理解.从具体的问题情境,引发学生的思考与探究.再从特殊的直角三角形入手,结合学生的已有知识经验,进行发散式猜想与探究,提出猜想,并通过几何画板进行数学验证.其次,在证明猜想的教学环节,让学生参与到课堂,采取小组合作的方式,分组对公式进行证明.在用向量法证明定理,肯定了学生的思路,力求让学生在课堂上能有收获和喜悦感.在证明过程中,让学生体会类比转化、分类讨论、数形结合等数学思想方法,并提高运用所学知识解决实际问题的能力.

2.1 基于思维发展,创设有效情景

古希腊学者亚里士多德说:“思维是从疑问和惊奇开始的.”对事物产生疑问是产生探究和思维的前提,成为创新思维的起点.对数学问题产生疑问,学生就会脱离大脑中的思维定势,不再受既有方法的束缚,通过对生活中的实际问题的独立思考和推理判断,得出正确的结论,从而发现解决新问题的途径,并能够提出自己的独特见解,提高思维能力,培育核心素养.

创设有效问题情境,注重以问题驱动学生数学思考.问题是数学的心脏,通过创设生活化的教学情景,提出测量两点之间距离的解决方法,在问题情境中设计了三个问题,三个问题环环相扣,激发了学生的求知欲,驱使学生积极主动探究出问题的解决方法.又运用最近发展区策略,把问题情境流畅的导入到学生熟悉的直角三角形,学生自主探究,提炼出了正弦定理的本质属性.

2.2 回归数学本真,培养核心素养

所谓本真,是指本原真实的原貌.数学课堂应该抓住数学本质,重视数学本质的揭示,关注学生学习生态,关注课堂动态生成,追寻属于数学教学的“本真”境界,积极构建高效生态课堂.数学课堂教学过分注重激发学生的兴趣,创设一些不切合学生实际的问题情境,致使问题情境形式花样繁多,令人眼花缭乱.这一现象使得数学课堂教学逐渐趋向低效或者无效,从而无法保证师生对话活动的有效性.教师没有遵循学生数学认知本真规律,忽视了学生发现、探究、解决问题的主动性,应从学生实际认知起点出发,符合学生学习规律有针对性地灵活施教,课堂教学“真”,促使学生数学学习真实、有效地“发生”,学生有了兴趣,才会主动参与.构建有利于学生思维发展的本真课堂教学结构,使数学课堂焕发生命的活力,使课堂形成提出问题、分析问题、解决问题的对话模式,涌动数学本真课堂的灵性.

2017版新课标的核心指导思想是以发展学生为本,注重学生核心素养的养成,现代的教育更应该顺应学生心理自然的发展,培养学生用“数学的眼光思考问题’’,“用数学的视角看待问题”,数学的教学不仅要应顺应学生心理自然的发展,还要调动学生的思维想象能力.叶澜教授说:把课堂还给学生,让课堂焕发出生命的活力.基于此,笔者觉得数学问题情境的创设更应该具有有效性,让学生形成综合和持久性的核心素养去设计,促进学生核心素养的达成.

但环顾当前数学教学,教师在课堂上没有给学生充足的时间去探索,学生实践探索的空间变窄,学生的学习热情受到严重打压.只有依托学情和教材内容,搭建合理的探究平台,关注学生的发展,促进学生数学核心素养的养育.

正弦定理的教学过程中,设计了一个学生比较熟悉的数学实际问题,根据情境,不停地改变情境,进行有效的追问,提高了学生的兴趣,使其快速地进入到研究者的角色.以“正弦定理的发现”为基本探究内容,引导学生按照由特殊到一般的探究思路,让学生的思维由问题开始,到猜想的得出,猜想的探究,定理的推导,并逐步得到深化.不断挖掘他们的潜能,让他们享受成功的喜悦.本节课创设了有效的问题情境,启发了学生的独立思考,形成和发展了数学核心素养.