数列强化训练B 卷参考答案

一、选择题

1.C 2.D 3.B 4.A 5.C 6.B

7.C 8.C 9.B 10.B 11.C 12.C

二、填空题

三、解答题

18.(1)设{an}的公差为d，由题意得3a1+3d=-15。

由a1=-7得d=2。

所以{an}的通项公式为an=2n-9。

(2)由(1)得Sn=n2-8n=(n-4)2-16。所以当n=4时，Sn取得最小值，最小值为16。

19.(1)由题意可得a1+3a2+…+(2n-1)an=2n。 ①

n≥2时，a1+3a2+…+(2n-3)an-1=2(n-1)。 ②

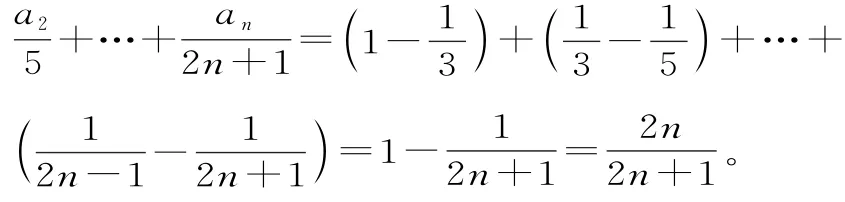
20.(1)当n=1时，a1=2S1+1=2a1+1，解得a1=-1。

当n≥2时，由an=2Sn+1，得an-1=2Sn-1+1，两式相减得an-an-1=2an，化简得an=-an-1。

所以数列{an}是首项为-1，公比为-1的等比数列，所以an=(-1)n。

(2)由(1)得bn=(2n-1)·(-1)n。

当n为偶数时，Tn=-1+3-5+7-

当n为奇数时，n+1为偶数，Tn=Tn+1-bn+1=(n+1)-(2n+1)=-n。

故数列{bn}的前n项和Tn=(-1)n·n。

21.(1)因为Sn=2an-a1，Sn-1=2an-1-a1(n≥2)，两式相减得an=2an-1(n≥2)。

故数列{an}是以2为公比的等比数列。

又因为a1，a2+1，a3成等差数列，所以a1+a3=2(a2+1)，解得a1=2，所以an=2n。

22.(1)因为a1=1，an+1=an+2，所以数列{an}是首项为1，公差为2的等差数列。

所以

an=1+(n-1)×2=2n-1。

已知Sn=2-bn。 ①

当n=1时，b1=S1=2-b1，所以b1=1。

当n≥2时，Sn-1=2-bn-1。 ②