巧用平面几何知识找中点证明线面平行

苏保明

证明线面平行是高考命题的重要内容之一，也是常考不衰的重要题型，深受命题专家的青睐，其原因是此类题错综复杂，能很好地考查考生的思维水平.本文根据初高中几何连接点的内在联系，从以下四个方面找线段的中点，进而顺利证明线面平行.

方法一：利用“对角线互相平分”找中点

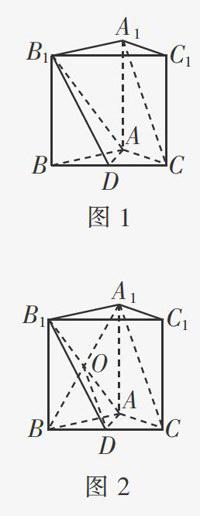
例1 如图l，底面是正三角形的直三棱柱ABC-A₁B₁C₁中，D是BC的中点，AA₁=AB=2.

（Ⅰ）证明：A₁C∥平面AB₁D.

（Ⅱ）（略）

（Ⅰ）证明：如图2，连接A₁B，交AB₁于点O，连接OD.

由于ABC-A₁B₁C₁是直三棱柱，所以四边形A₁B₁BA是矩形.故A₁O=OB（此结论用到了初中数学知识，即“矩形对角线互相平分”）.

由于BD=DC，所以OD是△A₁BC的中位线，可知OD//A₁C.又OD 平面AB₁D，A₁C 平面AB₁D，所以A₁C∥平面AB₁D.

小结 由于涉及矩形A₁B₁BA的对角线AB₁，联想到矩形A₁B₁BA的另一条对角线A₁B，所以连接A₁B，这样就可构造三角形的中位线，找到线线平行，从而顺利地证明线面平行.

值得注意的是，凡是涉及平行四边形、矩形、菱形、正方形的一条对角线，往往需要连接另一条对角线，这样可根据对角线互相平分找到边的中点.

方法二：利用“等腰三角形三线合一”找中点

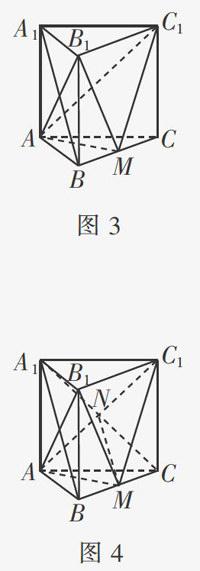
例2 如图3，直三棱柱ABC-A₁B₁C₁的底面是边长为a的正三角形，点M在边BC上，△AMC₁是以M为直角顶点的等腰直角三角形.

（Ⅰ）证明：直线A₁B∥平面AMC₁.

（Ⅱ）（略）

（Ⅰ）证明：如图4，连接A₁C，交AC₁于点N，连接MN.

由于ABC-A₁B₁C₁是直三棱柱，所以CC₁⊥平面ABC，四边形A₁C₁CA是矩形.又AM 平面ABC，所以CC₁⊥AM.由于AM⊥MC₁，CC₁ MC₁=C₁，CC₁ 平面BB₁C₁C，MC₁ 平面BB₁C₁C，所以AM⊥平面BB₁C₁C.又BC 平面BB₁C₁C，所以AM⊥BC.在△ABC中，由AB=AC，AM⊥BC，可知BM=MC（此结论用到了初中数学知识，即“等腰三角形三线合一”）.

由于点N是矩形A₁C₁CA的两条对角线的交点，所以A₁N=NC，则MN是△A₁BC的中位线，MN∥A₁B.又MN 平面AMC₁，A₁B 平面AMC₁，所以A₁B∥平面AMC₁.

小结 题目涉及对角线AC₁，就需要想到另一条对角线，所以连接另一条对角线A₁C，得到中点N.另外又涉及点M，所以可想到“如果M是BC的中点，那么MN就是△A₁BC的中位线”.这样一来，问题就迎刃而解了.其实也是如此，由AB=AC，AM⊥BC，可得M是BC的中点，这就用到了初中平面几何的知识“等腰三角形底边上的高与底边上的中线互相重合”.由此可见，熟练掌握初中数学知识，对解高中数学题很有帮助.

方法三：利用平行线分线段成比例定理找中点

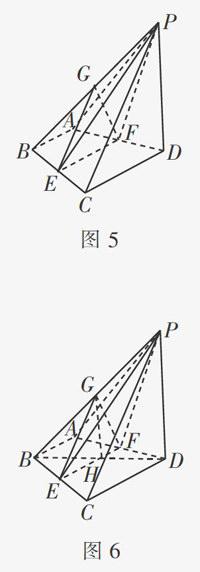
例3 如图5，在四棱锥P-ABCD中，平面ABCD⊥平面PCD，PD⊥CD，AB∥CD，AB=BC=AD=PD=1，CD=2，且点E，F，G分别是BC，AD，PB的中点.

（Ⅰ）證明：PD∥平面EFG.

（Ⅱ）（略）

（Ⅰ）证明：如图6，连接BD，交EF于点H，连接GH.

由于AB∥CD，AB≠CD，所以四边形ABCD是梯形.又E，F分别是BC，AD的中点，所以AB∥EF∥CD.由AF=FD，可知BH=HD（此结论用到了初中数学知识中的平行线分线段成比例定理）.

由PG=GB，可知GH∥PD.由于PD 平面EFG，GH 平面EFG，所以PD∥平面EFG.

小结 此题的证明用到了初中平面几何的平行线分线段成比例定理.由此找出三角形的一边的中点H，构造出三角形的中位线，进而较为轻松地证明了线面平行.

方法四：利用平行线分线段成比例定理的推论找中点

例4 如图7，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，PA=PD=2，BC=1/2 AD=1，CD= ，M是棱PC的中点.

（Ⅰ）证明：PA∥平面MQB.

（Ⅱ）（略）

（Ⅰ）证明：如图8，连接AC，交BQ于N，连接MN.

由于AQ=QD=1/2AD，BC=1/2AD，所以BC=QD.又BC∥QD，所以四边形BCDQ是平行四边形，BQ∥CD.在△ACD中，AQ=QD，NQ∥CD，所以AN=NC[此结论用到了初中数学知识中的平行线分线段成比例定理的推论，即“平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例”].

由于PM=MC，所以MN是△ACP的中位线，则MN∥PA.又MN 平面MQB，PA 平面MQB，所以PA∥平面MQB.

小结 此题证明的关键点AN=NC，就是用到了初中平面几何的平行线分线段成比例定理的推论.由此找出三角形一边的中点Ⅳ，从而一目了然地找到了三角形的中位线，使证明过程明朗化，

初中平面几何的相关知识是解决高中立体几何问题的关键点.因此，考生务必熟练掌握，在解题中熟练运用，不断提高自己的思维水平和解题能力.