基于关联规则挖掘Apriori算法的改进算法

周 凯, 顾洪博, 李爱国

(1.东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318; 2.大庆油田工程有限公司, 黑龙江 大庆 163712)

数据挖掘是指从大量的数据中筛出有效的、可信的以及隐含信息的高级处理过程。关联规则挖掘是数据挖掘的一个重要研究方向，侧重于确定数据库中不同领域间的联系，找出满足给定支持度和可信度的多个域之间的依赖关系[1-2]。由Agrawal等人提出的基于布尔关联规则挖掘频繁项集的Apriori算法，用由下到上逐层搜索的迭代方法查找频繁项集[3-5]。由于数据库本身的数据量较大，会存在多次扫描数据库以及多次迭代后产生大量候选集两个主要问题，最终导致算法效率不高。

国内外学者对挖掘频繁项集算法进行了大量的研究：于守键等[6]利用前缀项集的存储方式，通过哈希表快速查找来提高查找的效率。赵龙等[7]提出Apriori算法中会出现同一属性的不同属性值进行连接的情况，通过比较能提前判断是否有这种情况发生，这样避免重复连接的同时，也不需要再和数据库中的数据进行验证对比，节约了资源，提高了挖掘效率。屈鑫乙等[8]利用任何一个频繁k+1项集均可以表示一个频繁k项集与一个频繁1项集的交集这一性质，产生频繁项集。该改进算法减少了扫描数据库的次数并提高了算法的效率。边根庆等[9]通过富裕项和事务权重，计算项的权重支持度，从而得到频繁项集。

本文提出一种快速挖掘频繁项集的改进Apriori算法。该算法只需对事物数据库扫描一次，即可获得与该数据库对应的一个布尔矩阵，从而大量复杂数据的处理变为对0或1的处理，减少系统资源的占用[10]。通过布尔矩阵的行向量计算或者列向量计算两种方式，实现快速查找频繁项集的目的。不管采用行向量计算还是列向量计算，在挖掘过程中都采用尽可能压缩候选项集，删除其中的非频繁K-1项集元素，再产生频繁k项集的方式，其目的为节省运行时间，提高产生有效频繁项集的效率。

1 Apriori算法

设I={i1,i2,i3,…}是一个项目集合，事务数据库D={t1，t2，t3,…}是一系列事物，由唯一标识TID进行区分。每个事务ti(i=1,2,3,…)对应I上的一个子集。引用文献[5]中的事物数据库D，如表1所示。Apriori算法是利用逐层搜索的迭代方法，用k-1项集搜索k项集。搜索前要设定最小支持度，基本操作为：

表1 事务数据库D

(1)每个项都是候选1项集的集合C1，扫描数据库D，统计每一个项发生的数目，找出满足最小支持度的项，生成频繁1项集，计作L1；

(2)用L1与自己连接(L1∞L1)来生成候选2项集的集合C2，扫描数据库D，统计每一个项发生的数目，找出满足最小支持度的项，生成频繁2项集，计作L2；

(3)如此下去，直到不能找到频繁k项集Lk。

Apriori算法中满足关联规则挖掘的理论：频繁项目集的子集仍是频繁项目集；非频繁项目集的超集是非频繁项目集[5]。算法中的Ck是Lk的超集，也就是说Ck的成员可以不是频繁的，但所有的频繁项集都包含在Ck中，并且任何非频繁的(k-1)项集都不是频繁项集的子集。但是Apriori算法存在两个主要的缺陷：一方面在剪枝过程中，需要多次扫描数据库，需要很大的I/O负载，候选集Ck中的每个元素都必须通过扫描一次数据库来验证是否加入Lk；另一方面可能产生庞大的候选集，由Lk-1产生k候选集Ck是呈指数增长[6]。

2 Apriori算法的改进

2.1 生成数据库的布尔矩阵

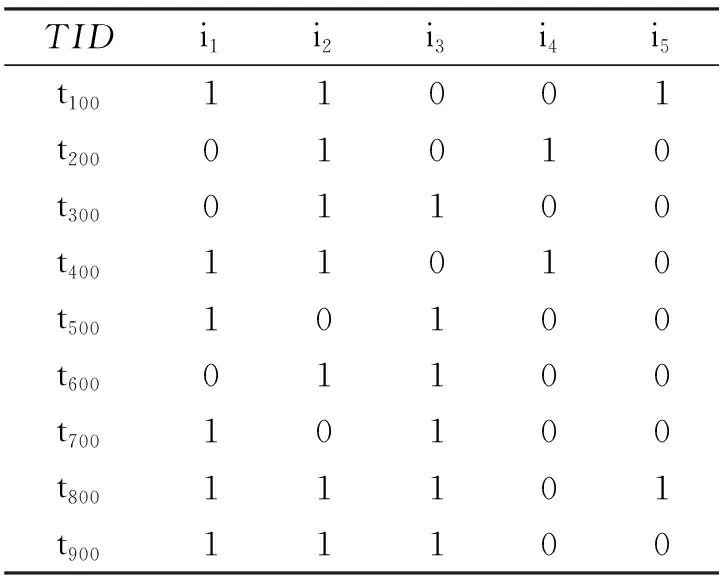
表2 数据库D对应的布尔向量矩阵

扫描事务数据库D，用事务表示行向量，项集表示列向量，若第i个事务中存在第j个项集，则第i行，第j列所对应的值就为1，否则为0，按照这种方式只需扫描一次数据库D，就可构造出与数据库相对应的布尔矩阵。根据表1所示内容，构造出如表2所示的布尔矩阵。

2.2 改进算法的描述

2.2.1 布尔矩阵的行向量算法

设项目集合中包含的项目数为m，通过表2计算事务数据库D中每项事务包含的项目的个数k(k≤m)，统计所有k值相同项的个数N，若N大于等于给定的最小支持数，则k为最大频繁项目的项目数，找出所有包含k项的候选项目集。接着分别判断这些项目集是否为频繁k项集，若某个频繁k项目集是频繁项目集，那么它的所有非空子集都是频繁项目集，即可找到所有的频繁项集。行向量算法流程如图1所示。

以表1中事务数据库D为例，用此方法计算出事务数据库的全部频繁项集。设最小支持数为2。由表2可得到每个事务中包含的项集的个数，如表3所示，最后一列为每项事务包含的项目的个数。

k=2时，包含的有5项事务(N=5)大于等于最小支持数，分别是{i2,i3}、{i2,i4}、{i1,i3}，由表4可得{i2,i3}、{i2,i4}、{i1,i3}的支持数大于等于最小支持数。所以频繁2项集为{i2,i3}、{i2,i4}、{i1,i3}。

k=3时，包含的有3项事务(N=3)大于等于最小支持数，分别是{i1,i2,i5}、{i1,i2,i4}、{i1,i2,i3}，同上方法，得{i1,i2,i5}、{i1,i2,i3}两项的支持数都大于等于最小支持数。所以频繁3项集为{i1,i2,i5}、{i1,i2,i3}。

等效电容C由开口间隙的距离、开口的横截面积以及金属环的介电常数决定，等效电感L则主要与金属环的周长与宽度有关。随着开口距离d的增大，等效电容随之减小，同时金属环的长度减小导致等效电感的减小，最终谐振频率随之增加，从而发生蓝移。图6（b）为高频谐振的Q值变化。随着开口距离d的增大，超材料的非辐射损耗随之减小，高频处谐振的Q值也进一步增大，由8.23增加到8.46再增加到10.32。环偶极子超材料的低损耗及高Q值有助于制备高效的超材料功能器件。

k=4时，包含的有1项事务(N=1)小于给定的最小支持数，所以事务数据库D中不包含项目数为4的项。

根据项目集是频繁项集，则它的所有非空子集都是频繁项目集的性质。所有频繁3项集、频繁2项集及它们的子集都是频繁项集。所以事务数据库D的频繁项集为{{i1}，{i2}，{i3}，{i4}，{i5}，{i1,i2}，{i1,i3}，{i1,i5}，{i2,i3}，{i2,i4}，{i2,i5}，{i1,i2,i3}，{i1,i2,i5}}。

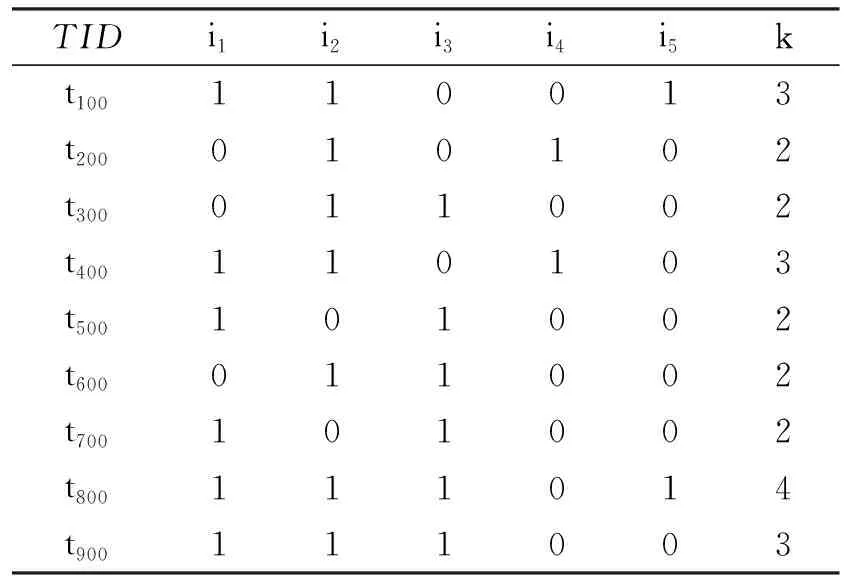
表3 每项事务包含项集的个数

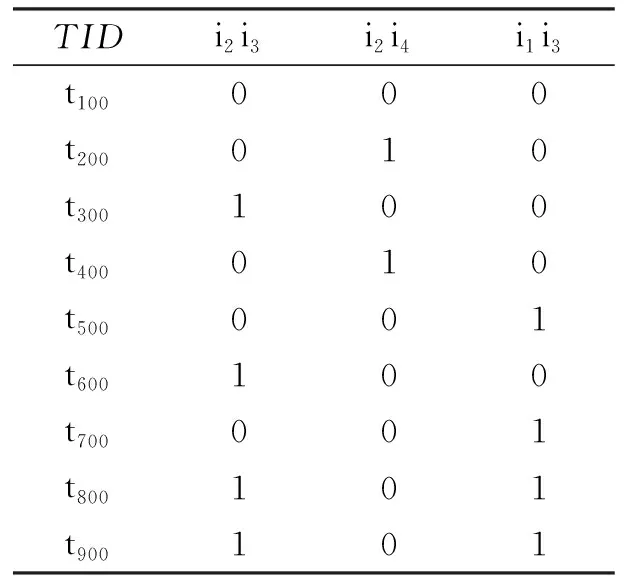
表4 候选项集的支持数

2.2.2 布尔矩阵的列向量算法

通过表2可以计算出项目集合I中的每个项出现的次数(即“1”的个数)，若大于等于给定最小支持度，则该项就属于频繁1项集。将频繁1项集中的任意两项进行“与”运算，所得的结果中若“1”的个数大于等于给定最小支持度，则这两项的组合就属于频繁2项集。以此类推，要求频繁k项集时，从已知的频繁k-1项集中任取2个符合条件的项进行连接，将连接后的项集中的各项进行“与”运算，其结果如果大于等于最小支持度，则该项即属于频繁k项集。列向量算法流程如图2所示。

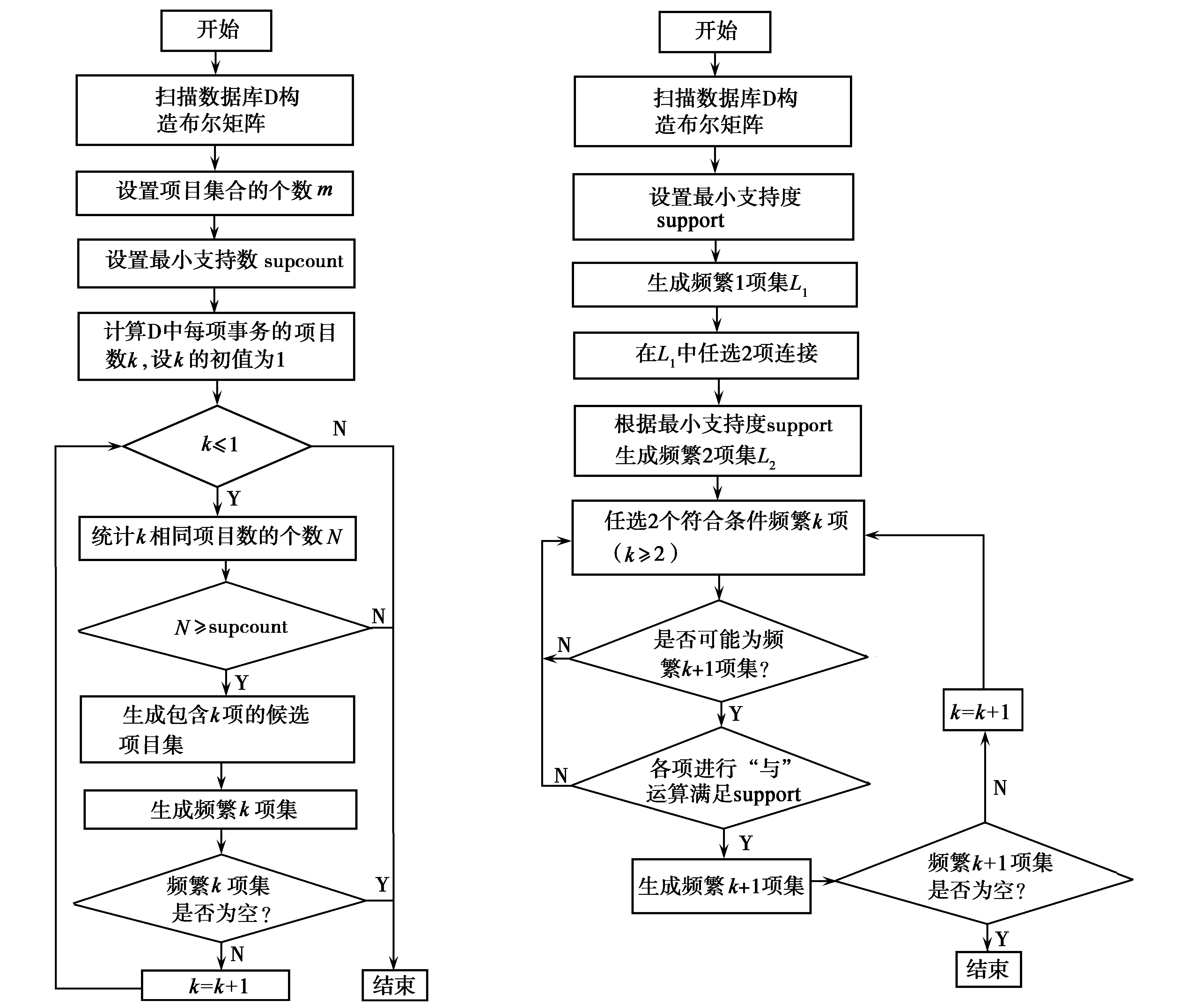
图1 行向量算法流程图 图2 列向量算法流程图

以表1中事务数据库D为例，用此方法计算出事务数据库的全部频繁项集。设定最小支持度为2。

由表2可得：i1=(100110111)，i2=(111101011)，i3=(001011111)，i4=(010100000)，i5=(100000010)，i1，i2，i3，i4，i5中“1”的个数分别为6,7,6,2,2，大于等于最小支持度，所以频繁1项集L1={{i1}，{i2}，{i3}，{i4}，{i5}}。

从频繁2项集L2中选择开始项相同的两个项集，如{i1,i2}、{i1,i3}，首先判断{i1,i2,i3}是否可能是频繁3项集，根据关联规则挖掘的理论：频繁项集的子集仍是频繁项集，即{i1,i2}、{i1,i3}、{i2,i3}都应存在于频繁2项集中。若满足该条件，则将i1∧i2∧i3运算所得的结果(000000011)与最小支持度进行比较，由于结果满足最小支持度的要求，{i1,i2,i3}属于频繁3项集L3。同理，{i1,i2,i5}满足要求，所以L3={{i1,i2,i3}，{i1,i2,i5}}。

从频繁3项集L3中选择开始项相同的两个项集为{i1,i2,i3,i5}，根据Apriori算法的性质，若{i1,i2,i3,i5}为频繁项集，则它的任意子集也应该是频繁子集，但是子集{i3,i5}不是频繁子集，所以{i1,i2,i3,i5}不是频繁4项集，也就是说频繁4项集L4为空集。

综上所示，该数据库事务D的频繁项集为{{i1}，{i2}，{i3}，{i4}，{i5}，{i1,i2}，{i1,i3}，{i1,i5}，{i2,i3}，{i2,i4}，{i2，i5}，{i1,i2,i3}，{i1,i2,i5}}。

2.2.3 算法性能分析

为了测试Apriori改进算法的性能，选取测试数据集Mushroom(事务数8124，每个事务有23项)作为实验数据，通过MATLAB平台进行算法性能测试。运行结果如图3、图4所示。图3所示中设定相同的事务数，在最小支持度不同的情况下，挖掘频繁项集所花费的时间的比较；图4中采用相同的支持度，在事务数不同的情况下，挖掘频繁项集所用的时间比较。通过实验证明，由于改进后的算法只需对数据库进行一次扫描，并且采用行向量或列向量挖掘过程中通过尽量压缩频繁k-1项集，提高频繁k项集的挖掘效率，提高运行速度。同时数据集Mushroom中的数据相关性较强，改进的Apriori算法也能较好地进行频繁项集的挖掘，完全优于原有的Apriori算法。

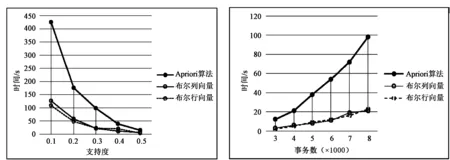
图3 不同支持度下Apriori算法与改进算法性能比较 图4 不同事务数下Apriori算法与改进算法性能比较

3 结束语

本文提出了基于布尔矩阵的行向量和列向量两种方式的改进Apriori算法，该算法扫描一次数据库后，将数据库转化为布尔矩阵，不但节省了大量内存，而且避免了传统算法总多次扫描数据库的缺陷；同时在通过行向量和列向量方式生产频繁k项集前，对频繁k-1项集进行压缩，尽可能删除非频繁k-1项集。改进算法意在解决原Apriori算法中的两个主要问题，大大节省挖掘频繁项集的时间，提高了算法的效率。数据挖掘面向的是大量的数据，本文只是以测试数据为例，提出了详细的频繁项集的生成过程。在实际应用的过程中，可以参考此方法完成对大量数据的挖掘，这也是下一步的工作之一。