真空预压吹填淤泥地基均匀性的离散元模拟
2018-11-06习志雄杨贝贝
习志雄, 杨贝贝
(1.中交第一公路工程局有限公司, 北京 100024; 2.北京城建设计发展集团股份有限公司, 北京 100037)
为了缓解沿海地区土地资源紧张的问题,部分交通、岩土等工程进行了填海造陆。在众多填海造陆方法中,采用中粗砂进行吹填造陆的方法具有成本低、工期短、效果良好等特点。然而,由于砂土产量有限,可考虑采用疏浚淤泥作为吹填料[1]。吹填淤泥具有含水率高、孔隙比大、抗剪强度低、压缩系数高、渗透系数小等特点。因此,在吹填淤泥质软土地基上兴建工程,需要解决的关键问题就是将地基承载力提高到设计要求[2-3]。提高吹填软土强度的方法较多[4-5],对于大范围的软基处理问题而言,真空预压法具有较好的经济性[6]。
1952年,Kjellman[7]首先提出了真空预压法。其后,研究者们对吹填土加固效果的影响因素[8-9]、吹填土加固过程数值计算[10-11]、吹填土固结模型[12-13]等进行了相关研究。这些研究内容揭示了吹填土在真空预压法加固过程中固结机理、固结特性等。对于真空预压吹填淤泥地基而言,在排水板周围会形成“土柱”。“土柱”具有高强度、高密实度、弱透水性等特点。然而,随着土体与排水板间距的增加,“土柱”外的土体性质变化较小。从而造成地基整体强度偏低,达不到设计要求。然而,关于这方面的研究相对较少。
本文基于真空排水预压处理软土地基理论,应用离散元数值方法模拟真空预压过程中土体的固结效果,并研究排水真空度等因素对固结后土体孔隙率不均匀变化的影响。其次,为了提高真空预压固结的效率,依据数值模拟的结果提出一种新的真空固结吹填淤泥地基的施工工艺。
1 数值模型
为了研究真空预压过程中土体的固结效果,采用离散元数值计算软件对其进行模拟。关于离散元方法和模拟过程的介绍可参见文献[14-16]。真空预压法处理吹填淤泥质软土地基的断面及计算单元如图1所示。取某深度下两个塑料排水板间单位厚度的土体,即图1中阴影部分,作为计算对象。考虑到研究对象的对称性,可取相邻两个排水板间土体的一半作为计算单元即可。此处忽略了竖向渗流,仅考虑水平向渗流。计算中用圆形颗粒模拟土颗粒,用点墙达标排水板。计算单元的上下表面设置为不透水边界,并且在右侧边界施加负压,以此形成压力差来模拟真空抽水负压。计算中材料参数取值见表1。
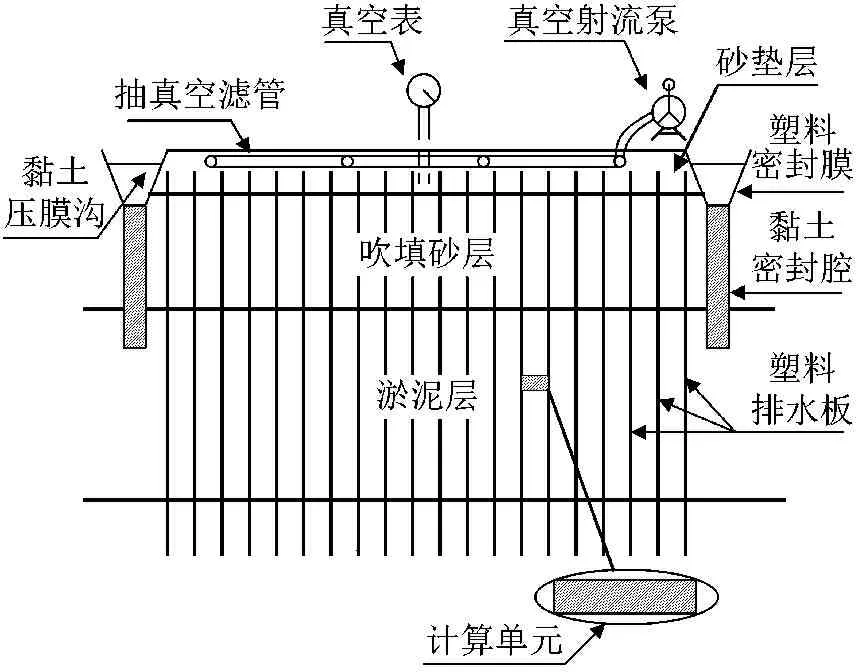

图1 断面及单元示意图
2 不同工况下土体均匀性分析
在渗流的过程中会产生渗透力,此时土颗粒会发生移动,伴随着土颗粒的重排列、沉积,并且土体的孔隙率、渗透性发生变化。为了反映这一复杂的水土相互作用的过程,图2给出了不同计算步的土颗粒流迁移模拟结果。其中,计算步的增加代表时间的增长。在渗流的作用下,土颗粒逐渐向右端移动,即水流上游处土体孔隙率增加,水流下游处土体孔隙率减小,并最终导致土体的不均匀性。本节讨论抽水真空度P、排水板间距L、土体孔隙率n0对真空预压固结地基的土体均匀性的影响。
2.1 抽水真空度P
此处对比给定排水板间距(0.45 m、0.55 m)和初始孔隙率(0.4、0.6)下,真空度从20 kPa到100 kPa变化时,真空排水模拟计算40 000步后,土体内各区域孔隙率随真空度的变化情况。为了反映孔隙率离散程度,计算五个区域孔隙率的标准差。标准差的计算结果如图3所示。其中,图3图例的两个数值分别代表排水板间距(单位m)及初始孔隙率。图3表明在不同真空度下,各区域的孔隙率偏离平均孔隙率的离散程度并不相同。不同区域内土体孔隙的均匀性随着抽水真空度的增加而降低。

图2断面及单元示意图土体颗粒流迁移模拟图

图3真空度与孔隙率标准差关系曲线
2.2 排水板间距L
此处对比给定初始孔隙率(0.4、0.6)和抽水真空度(50 kPa、100 kPa)下,排水板间距从0.8 m到1.2 m变化时,孔隙率均匀性随排水板间距的变化规律。计算结果如图4所示。其中,图4图例的两个数值分别代表初始孔隙率及抽水真空度(单位kPa)。图4表明当初始孔隙率较大时(n0=0.6),各区域内土体孔隙分布的均匀性随着排水板间距的增加而提高。当初始孔隙率较小时(n0=0.4),存在一最优排水板间距。当排水板间距取最优值时,预压固结后土体的均匀性最好。
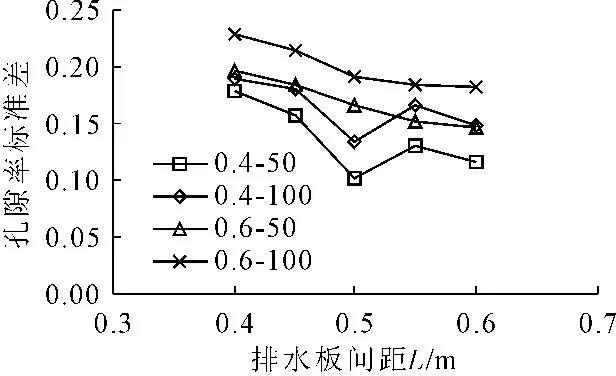
图4排水板间距与孔隙率标准差关系曲线
2.3 初始孔隙率n0
此处对比给定抽水真空度(50 kPa、100 kPa)和排水板间距(0.45 m、0.55 m)下,初始孔隙率n0从0.3到0.7变化时,真空排水模拟计算40 000步后,土体内各区域孔隙率随真空度的变化情况。计算结果如图5所示。其中,图5图例的两个数值分别代表抽水真空度(单位kPa)及排水板间距(单位m)。图5表明当初始孔隙率较小时,真空预压排水后土体比较均匀。随着初始孔隙率的增加,排水预压后土体各区域孔隙率的均匀性降低。由于欠固结的吹填淤泥质土的初始孔隙率较大,因此不宜采用原有的真空预压法对其进行处理。
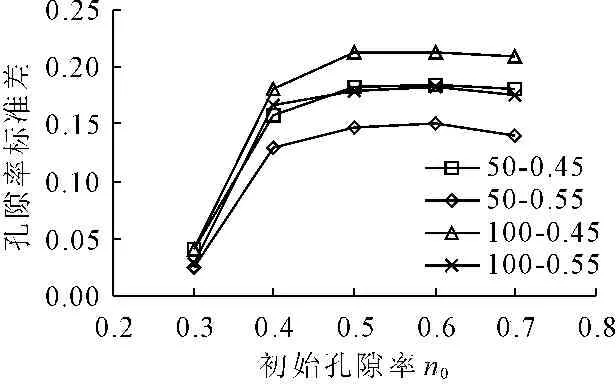
图5初始孔隙率与孔隙率标准差关系曲线
3 排水板打设施工新工艺
前文讨论了抽水真空度等因素对真空预压固结后土体孔隙率均匀性的影响程度。上述结果表明排水板间土体孔隙率的均匀性会随着排水板间距的增加而提高。然而,随着排水板间距的增加,固结效果显著降低,并且固结时间显著提高。针对这种情况,此处提出一种新的布设排水板的施工工艺。首先,以两倍的原排水板间距布设排水板,并进行第一次的真空预压过程。当排水固结稳定后,在排水板中间布设新的排水板,并进行第二次真空预压过程。第一次及第两次打设排水板真空预压法后孔隙率分布示意图分别如图6和图7所示。

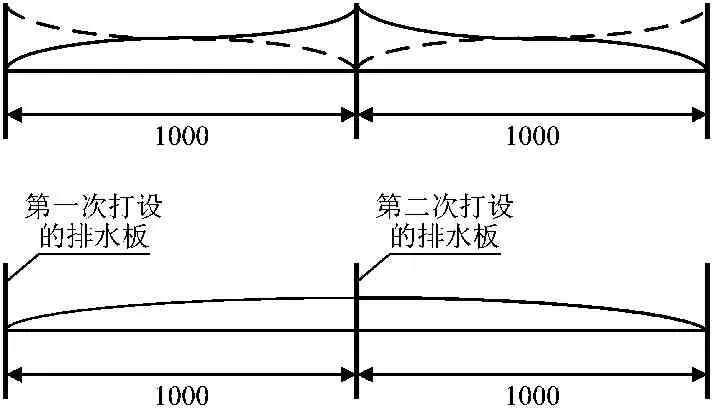
图6 一次打设排水板孔隙率分布示意图(mm)
图7两次打设排水板孔隙率分布示意图(mm)
考虑到计算问题的对称性,取其一半作为计算单元,单元的宽、高分别为1 000 mm、100 mm。模型中流体单元个数为1 000个,各单元尺寸为10 mm×10 mm。假设单元上、下表面是光滑的,因此上、下表面处平行于墙的水流流动速度不等于0。单元左右两侧分别施加0 kPa和-50 kPa的水压力。在这组水头差的作用下,土体内自左向右发生渗流。当第一次真空预压结束,即计算40 000步后,在相邻的排水板中间进行第二次布设。在第一次布设的排水板一侧施加0 kPa的水压力,在第二次布设的排水板一侧施加-50 kPa的水压力。此时,形成的压力水头差方向与之前的相反。
图8为五个区域孔隙率随计算步数的变化情况。在第一次打设排水板真空预压的过程中,土颗粒随着水流向排水板逐渐移动。然而,土颗粒的迁移却引起排水板间土体不均匀分布,表现为土体的密实程度随着与排水板距离的增加而降低。在第二次打设排水板真空预压的过程中,颗粒产生反向运动,提高了土体的均匀性。图9展示了第一次和第二次抽真空后多个区域土体的孔隙率分布规律。图中表明第二次预压后土体的均匀性和密实程度均得到了显著的提高。

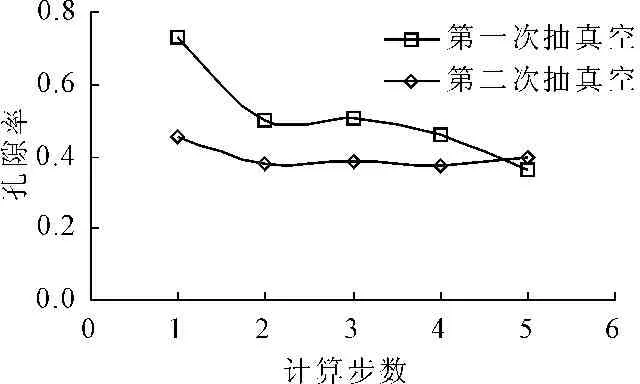
图8 5个区域孔隙率随时间的变化
图9两次抽真空结束后5个区域的孔隙率曲线图
4 结 论
(1) 真空预压后土体的均匀性随着抽水真空度的增加而降低。因此,施工时应根据土体均匀性的要求设置真空度的上限。
(2) 对于具有高初始孔隙率的土体而言,真空预压后土体的均匀性随着垂直排水板间距的增加而提高;对于低孔隙率的土体而言,存在一最优排水间距。
(3) 真空预压后土体的均匀性随着初始孔隙率的增加而降低。当初始孔隙率超过界限值后,不建议采用真空预压施工工法。
(4) 提出的布设排水板的施工工艺通过增加布设排水板的次数,有效地提高了吹填淤泥地基均匀性。
