基于自适应差分进化算法的水稻物候期预测模型参数自动校正

姜海燕，赵空暖，汤 亮，李玉硕，杨 华



基于自适应差分进化算法的水稻物候期预测模型参数自动校正

姜海燕1,2，赵空暖1，汤 亮2，李玉硕1，杨 华1

（1. 南京农业大学信息科技学院，南京 210095；2. 南京农业大学/国家信息农业工程技术中心，南京 210095）

进化算法在作物模型参数校准领域已有广泛应用。由于作物模型的结构包括多组常微分方程，具有非线性、不连续、多峰值特点，因此针对作物模型特点选择合适的进化算法尤为重要。同时，进化算法自身参数对算法性能有较大影响，这些参数选择往往靠经验得出，增加了优化算法在模型参数校准过程中的不确定性。该文针对进化算法应用到作物物候期模型参数校准过程中存在着算法选择和算法参数不确定性问题，以水稻RiceGrow物候期模型为应用对象，分析比较了3类进化算法应用的精度、收敛速度以及稳定鲁棒性。比较的进化算法包括差分进化系列算法（标准差分进化算法和自适应控制参数改进差分进化算法），协同进化遗传算法系列（个体优势遗传算法、M-精英协同进化算法）以及粒子群算法系列（标准粒子群算法、基于自主学习和精英群的多子群粒子群算法）。研究利用武育粳、雪花粘等5个品种在江苏宜兴、兴化和广东高要等不同生态点的多年田间试验资料展开量化分析。结果表明：1）利用自适应控制参数改进差分进化算法校准水稻物候期模型的品种参数准确性较高，算法自身参数易于确定。物候期模型校准以后在拔节期、抽穗期、成熟期的RMSE为1.7～4.6 d、NRMSE为1.8%～5.8%、MAD 为 1.4～3.3 d、2为 0.977～0.997，比GA系列平均分别小0.634d、0.608%、0.453d、0.09%，比PSO系列平均小1.399d、1.35%、1.039 d、0.23%。 2）自适应控制参数改进差分进化算法在水稻物候期模型参数校准问题上表现出良好的收敛速度及稳定鲁棒性。重复校准试验100次的目标函数标准偏差趋近于0，每次校准得到的品种参数值标准偏差较其他算法最小。在达到同样精准度的情况下，比标准差分算法收敛速度平均快117代，适用于实际应用实践。

作物；模型；气象；自适应控制参数；差分进化；进化算法；物候期模型；参数校准

0 引 言

物候期预测为作物生长模型预测提供统一时间尺度的衡量标准，是分析气候变化对作物生长发育时间影响的重要方法[1]。物候期模型模拟结果受到作物品种和温光环境等多因素的影响，模型的本地化应用存在着不确定性[2-3]，主要表现在数据不确定性、模型结构不确定性以及模型参数不确定性3个方面[4-5]。模型参数不确定性是指受到不同自然环境条件、不同栽培管理方式以及作物品种多样性的影响，参数值无法直接测量且有多种可能的组合[6-7]。虽然在以往的研究实践中，作物建模专家明确了模型参数的取值范围，但是在实际应用中，还需要结合先验知识进一步确定出物候期模型品种参数的最优解。这项工作费时费力，人工操作往往会忽略最优解。因此，在不确定条件下对模型参数实现自动校准是提高作物模型在本地应用适应性与精度的重要技术手段[8-9]。

作物模型参数校准主要包括基于统计推断理论的方法[10]和基于最优化理论的方法[1,11]。基于统计推断理论的方法主流是贝叶斯统计估算，如马尔科夫蒙特卡罗方法（Markov Chain Monte Carlo，MCMC）、普适似然不确定估计法（general likelihood uncertainty estimation，GLUE）等，已被广泛应用于WOFOST、RZWQM2、STICS等模型的参数优化[10,12-13]。该类方法的优点是可以对模拟结果进行不确定性分析和量化，给出模型参数的后验概率分布，但缺少最优解的直接推荐；基于最优化理论是指通过优化算法在模型参数空间分布上实现自动搜索，并按照一定的寻优规则识别较优或最优的参数集合。常用方法包括最小二乘法等传统优化方法以及遗传算法（genetic algorithm，GA）、粒子群优化算法（particle swarm optimization，PSO），差分进化算法（differential evolution，DE）等进化算法。以改进的非线性最小二乘法为基础的PEST（parameter estimation）参数自动优化工具，在作物模型和水文模型参数优化研究中得到了广泛应用[14-15]。但在参数太多或模型结构太复杂时往往无法收敛到最优值[16]。作物物候期模型具有非线性、非凸以及参数之间相关等特点，模型参数优化问题可以转化为有约束的多模态函数优化问题[17]，利用全局优化方法如进化算法（GA、DE、PSO）可以提供近似全局最优解。Soundharajan等[18]利用标准GA对ORYZA2000模型参数实现了自动校准，校准后的参数能够适用正常灌溉和水分胁迫下的模拟。庄嘉祥等[19]提出了一种改进型协同进化GA算法，个体优势遗传算法（individual advantages genetic algorithm，IAGA），突出了精英个体的引导能力，应用到RiceGrow和ORYZA2000物候期模型的参数校准中，提高了模型应用的精确程度。Zúñiga等[17]比较了差分进化算法（DE）、协方差矩阵适应进化策略（covariance matrix adaptation evolution strategy，CMA-ES），粒子群优化（PSO）和人工蜂群算法（artificial bee colony，ABC）应用于SUCROS生长模型的参数估计效果，发现应用DE算法的结果误差最小。综上，进化算法作为一类智能的全局最优化算法，具有自组织、自学习等特性，可以在一定迭代次数内找到最优解或近似最优解[20]，在作物模型参数校准领域已经有了广泛应用。作物模型的结构包括多组常微分方程，具有非线性、不连续、多峰值特点[21]，进化算法的应用效果通常取决于对特定类型问题的适应能力，因此针对作物模型特点选择合适的进化算法尤为重要。与此同时，进化算法自身参数对算法性能有较大影响，这些参数选择往往靠经验得出，增加了优化算法在模型参数校准过程中的不确定性。本文针对在作物物候期模型参数自动校准过程中，如何选择进化算法以及如何确定优化算法自身参数的问题展开研究，以RiceGrow物候期模型为对象，在不同生态点、不同品种多年物候期数据集下，比较分析利用不同类型进化算法进行品种参数校准的试验数据，选择具有自适应优化策略的进化算法，以期降低进化算法自身参数确定的经验性，增强算法应用的适应性。

1 材料与方法

1.1 试验站点和数据

试验数据如表1所示，南京2007—2008年的两优培九和宜兴1994—2011年的武育粳来源于国家信息农业工程技术中心水稻田间试验资料。兴化2001—2004年的武育粳3号、高要1997—2002年的芦丝占和高要2004—2009年的雪花粘品种的实测数据来自中国气象局气象数据中心汇总的全国各水稻种植区田间试验资料。其中，拔节期、孕穗或抽穗期和成熟期等物候期数据作为模型参数校准的实测数据。

气象数据集：江苏兴化、南京及广东高要3个站点的逐日气象资料，来源于国家气象局气象信息中心。江苏太湖稻区（宜兴）和溧阳的逐日气象数据来源于江苏省气象局。气象资料包括日最高温度（℃）、日最低温度（℃）、日照时数（h/d）、降水量（mm）等。各水稻品种信息及在实测年份内平均物候期天数和标准差见表1。

表1 试验站点及水稻品种栽培信息

注：–表示无数据。 Note: – no data

1.2 RiceGrow物候期模型

RiceGrow模型[22]是南京农业大学国家信息农业工程中心研制的水稻生长模拟模型的简称。RiceGrow物候期模型以水稻发育生理生态过程为基础，以生理发育时间（physiological development time，PDT）作为定量水稻发育进程的通用尺度，量化温度、光周期以及品种遗传特性对作物发育的影响，引入了5个品种参数（表2）。

表2 RiceGrow物候期模型的主要参数

1.3 基于进化算法的作物模型参数校准框架

作物物候期模型主要是量化温光对发育阶段的影响，其建模以生理生态过程为理论依据，利用非线性数学方程表示。对于C3作物而言，虽然稻麦等不同作物类型或者同类作物的不同模型的计算公式不同，但均具有类似的光合过程，其模拟过程类似。从抽象的最优化角度来看，是包含多组带约束条件的常微分方程组的非线性复杂过程模型，暂时无法获得目标函数相对于待优化变量的数学导数解析表达式，其计算过程不可微，具有非凸、非线性特点。因此，这类问题更适合于用全局启发式优化算法，如GA、DE、PSO等，近似求得全局最优解。

作物模型参数校准框架采用进化算法与作物模型耦合的方式。将待调参数作为待优化对象，当模型模拟值与实测值之间差值最小时，目标函数值所对应的参数值即为模型参数最优值，如图1所示。进化算法初始化种群作为作物物候期模型初始参数值，在气象和田间管理数据驱动下，运行模型获得模型输出模拟值。模拟值与实测值之间的误差作为种群个体适应情况的评价指标，通过不同的进化策略，进一步更新种群个体信息，将更新得到的新一代种群个体做为新的模型参数，重新代入模型计算，反复重复上述过程。当达到收敛标准或者设置的最大进化代数时，程序停止运算，此时最小目标函数值所对应的参数值即为最终所求模型参数。

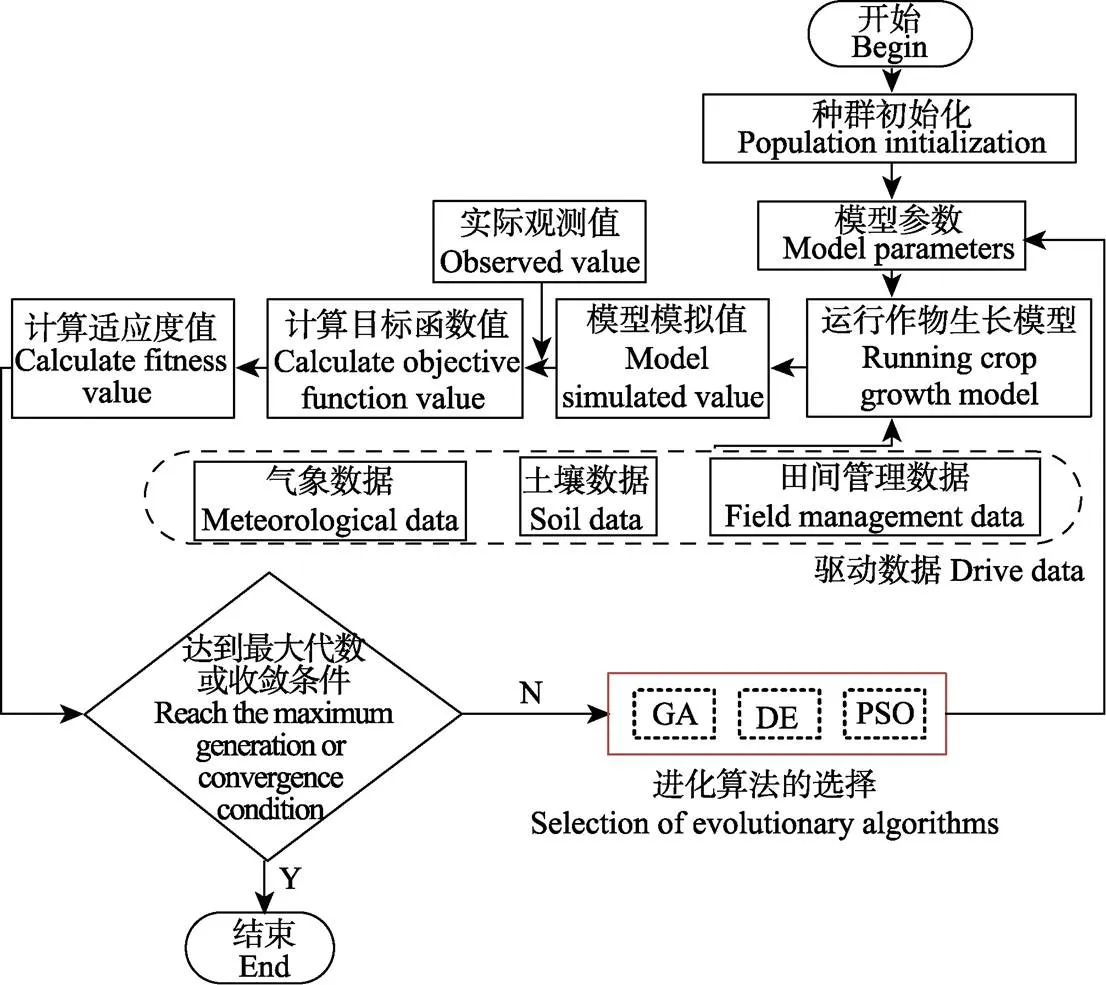
图1 基于进化算法的作物模型参数校准框架

1.4 自适应控制参数的改进型差分进化算法

差分进化算法（DE）是一种利用浮点矢量编码在连续空间中随机搜索的优化算法[23]。该算法原理简单，算法参数少，变异过程有效利用了群体分布特性，算法的搜索能力提高。Vesterstrom等[24]将DE与PSO和其他进化算法用34个广泛应用的Benchmark Problems进行了深入的比较研究，试验结果表明，DE的性能优于PSO和其他进化算法。DE已成为一种求解非线性、不可微、多极值和高维的复杂函数的有效和鲁棒的方法。已有研究表明DE算法在作物模型参数校准问题上也表现出良好的性能[17]。标准DE算法参数的确定是根据经验选取一组固定值，在优化过程中没有变化，无法较好地满足进化过程中算法性能对控制参数的特殊要求。自适应控制参数改进差分进化算法（self-adapting control parameters modified differential evolution algorithm，SCPMDEA）算法将自适应控制参数策略与差分进化算法结合，算法自身参数随进化个体适应度的变化而自适应地调节，避免了原DE算法参数的确定对具体优化问题的依赖性，提高了算法的鲁棒性。同时SACPMDE改进变异操作的策略，将随机选择的3个个体中适应度最优的个体作为变异的基矢量，而另外2个个体生成差分矢量，利于提高算法的收敛速率。算法详细细节见参考文献[25]。

1.4.1 差分进化算法参数的自适应策略

如图2所示，SACPMDE算法有2个算法参数：交叉概率因子（CR）和缩放因子（），均在进化过程中动态计算。在种群更新中根据个体适应度与整个种群适应度的平均值的比较计算来动态更新CR值，见式（1）。迭代过程中若个体适应度小于平均适应度，说明个体较优，CR应该取较小的值，避免该个体结构遭到过多的破坏；若个体适应度大于平均适应度，说明该个体较差，CR应变大一些，使之接受更多变异个体的基因，促使该个体的进化。

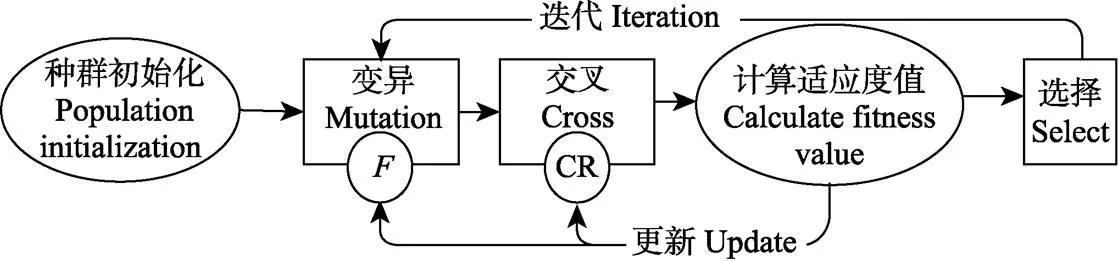
注：CR为交叉概率因子，F为缩放因子。

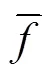
在变异操作中，根据随机选择的3个个体的相对位置来动态自适应地调节，见式（2）。如果随机选择的3个个体的位置相邻很近，则生成的变异矢量很小就起不到变异的效果，此时应选择较大的；如果3个个体的位置很分散，则应该选择较小的，避免生成的变异个体超出变量的搜索空间。

式中f、f、ftw分别为3个个体的适应度。F= 0.1，F= 0.9为F的上下限。

1.4.2 目标函数及惩罚函数设计

1）目标函数设计

作物物候期模型参数校准是通过极小化目标函数使得模型模拟值和实测值之间达到最佳拟合程度。本文把多个物候期模拟值和实测值之间的根均方差（root mean square error，RMSE）作为目标函数Fitness的计算公式。

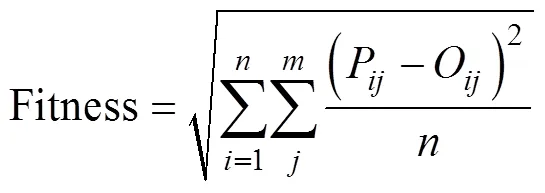
2）惩罚函数设计

基于水稻栽培知识及作物模型专家的经验，一般认为某一物候期的模拟误差超过6 d，该套参数模拟效果极差[19]。种群更新时，对于这样的个体，采用惩罚函数进行约束，将其目标函数增大一倍，增加其淘汰的速率。

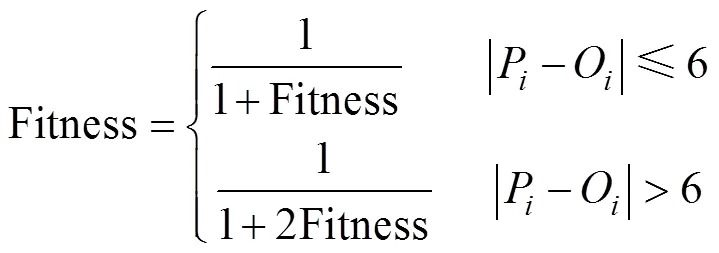
1.5 模型参数校准结果的检验与评价

模型参数校准后，选用通用的指标体系进行检验和评价[26-27]。通过1:1图直观地判断模型模拟值与实测值之间的吻合程度，对模型进行定性的总体评价。其次，选择统计指标进行定量化评价，统计指标包括模拟结果与实测结果的平均值，标准差（standard deviation，STD），两者之间的线性回归系数、截距、确定性系数2（determination coefficient）、均方根误差（root mean square error，RMSE）、标准均方根误差（normalized root mean square error，NRMSE），均绝对误差（mean absolute difference，MAD）。模拟误差的大小可由均方根误差（RMSE）与归一化均方根误差（NRMSE）反映，总体模拟效果由模拟值均值与实测值均值的差异反映，离散程度由标准差反应。当确定系数（2）越大时，吻合度就高。

1.6 试验设计及试验环境

本文设计2组试验比较分析不同进化算法在RiceGrow物候期模型参数自动校准应用中的有效性、收敛代数及稳定性。所有试验均在自主开发的调参工具下运行，运行环境是Intel(R) Core(TM) i5-7200U CPU@ 2.50 GHz，内存8 GB，windows10 64位操作系统。

试验采用3类全局优化进化算法，包括协同进化遗传算法系列，粒子群算法系列和差分进化算法系列（表3）。算法参数初始值是根据相应文献研究给出的经验值。试验选取隔年数据作为训练数据集，剩余隔年作为验证数据集。各算法校准试验种群大小均为100，最大迭代次数500，重复试验100次，得到100套参数解集，分别驱动模型验证计算评价指标，计算各评价指标平均值、最大最小值和标准偏差。量化分析不同进化算法在作物模型参数校准过程的有效性，收敛速度和算法稳定性等。

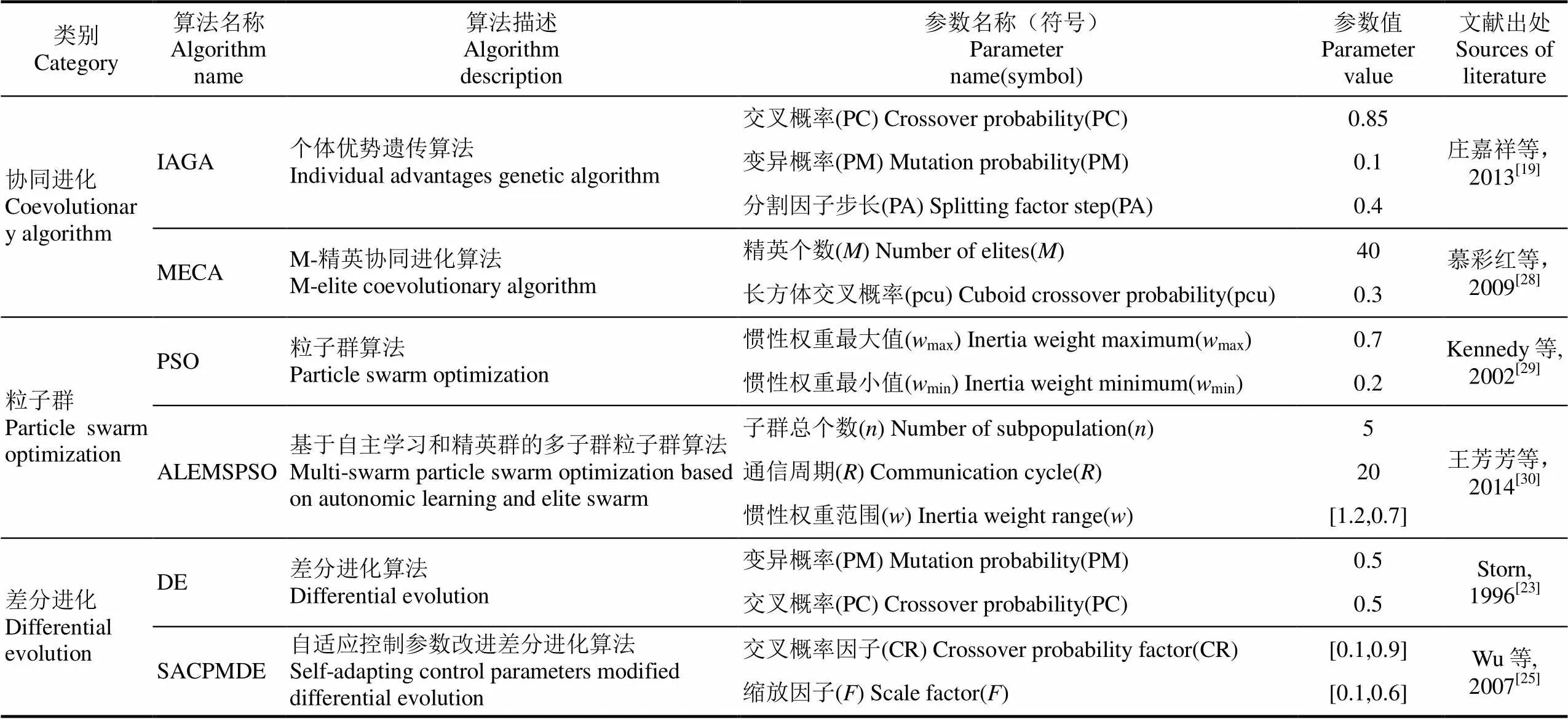
表3 待比较的进化算法描述和算法参数值及出处

2 结果与分析

2.1 比较多种进化算法对物候期模型参数校准的有效性

本文在给定的物候期模型参数初始范围内随机生成初始种群，作为模型参数初始值，对作物模型进行参数校准。

表4表示各进化算法在不同生态点不同品种训练数据集下100次重复试验得到的平均收敛代数、品种参数的平均值、标准偏差，以及验证后的平均评价指标。可以看到各算法均在500代以内收敛。DE系列的验证评价指标RMSE、NRMSE、MAD较小，比GA系列分别小0.2～3 d，0.2%～3%，0.2～1 d，比PSO系列分别小0.03～5 d，0.02%～5.03%，0～3.6 d，表明差分进化算法应用于RiceGrow物候期模型品种参数校准结果较好。其中利用SACPMDE进化算法校准后验证评价指标RMSE为 1.7～4.6 d，NRMSE为1.8%~5.8%，MAD 为 1.4～3.3 d，2为 0.977～0.997，比GA系列分别平均小0.634 d、0.608%、0.453 d、0.09%，比PSO系列平均小1.399 d、1.35%、1.039 d、0.23%。另外，利用DE系列算法参数校准后得到的品种参数值的标准偏差都是最小的。5个品种参数的标准偏差均小于1，说明应用DE系列算法多次调参所获得的物候期模型参数校准结果基本趋于同一组参数，表明该类算法应用的稳定性好。其次是协同进化遗传算法系列，准确度和稳定性相对较好，而利用PSO系列的校准误差相对较大及算法稳定性较差，特别是当训练数据集较少时（如两优培九训练数据集只有2 a实测数据）的参数校准误差都在6 d以上。SACPMDE在兴化的武育粳，高要的雪花粘，南京的两优培九数据集校准下的RMSE均在1 d～3.2 d，NRMSE在1%～2.9%，MAD在1～3 d，2都在0.97以上，均比标准DE小。

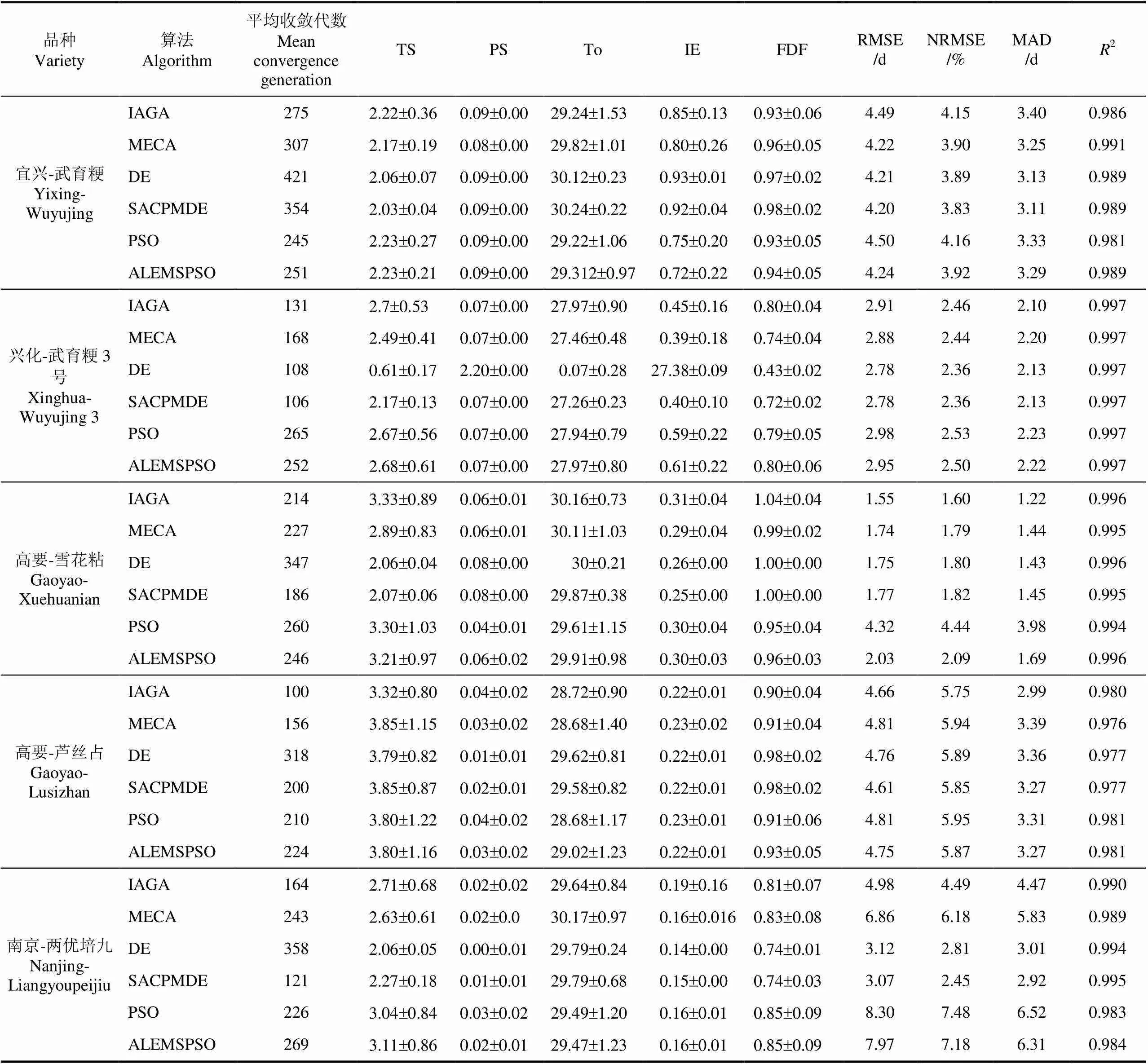
表4 不同水稻品种校准后模型参数的平均值及验证数据集下的评价指标

注：文中数据以均值±标准偏差形式表达。

Note: The data are expressed in terms of mean±standard deviation.

2.2 比较多种进化算法对模型参数校准的稳定性及收敛速度

图3为应用不同进化算法校准物候期模型参数时，在不同训练数据集下的目标函数最优值、最差值、平均值以及目标函数值的标准偏差。可以看出：差分算法系列其目标函数平均值最小，而目标函数最优值、最差值及平均值反应了算法的优化效果优劣，再次表明DE算法系列在RiceGrow物候期模型品种参数校准上的有效性。DE算法在宜兴武育粳、兴化武育粳3号、高要雪花粘、高要芦丝占和南京两优培九数据集上模型参数校准的目标函数最优值分别为8.76、0.4、2.6、1.52和2.51，而SACMPDE算法参数校准结果的目标函数最优值为8.65、0.4、2.6、1.52和2.08，结果表明SACPMDE的目标函数最优值优于标准DE算法。

目标函数值的标准偏差反映了算法应用的稳定性，DE系列目标函数标准差都基本接近0，特别是SACPMDE在兴化武育粳3号和南京两优培九数据集上目标函数标准偏差都为0，说明算法的稳定性好，可以在有限时间范围内找到近似最优解。另外在达到相同精准度下，DE和SACPMDE分别的收敛代数为421、108、347、318、358和354、106、186、200、121，SACPMDE收敛代数要比DE收敛代数分别小67、2、161、118、237，可以看出SACPMDE算法比DE算法收敛的快。其次协同进化遗传算法系列IAGA和MECA收敛代数相对较快，但其目标函数标准偏差在0.077～0.508范围内，原因可能是提早收敛到一个局部最优解，算法不够稳定。而PSO算法系列的目标函数值和标准偏差较前2类算法都大，表明在PSO系列在应用到RiceGrow物候期参数校准上模拟精度较低同时算法寻得最优解的能力相对不稳定。

通过3类进化算法分别对RiceGrow物候期模型进行参数校准，重复试验100次的目标函数值随迭代次数增加画出其收敛曲线。图4是以宜兴武育粳隔年8 a数据做训练数据集，选取2个算法试验100次以后作出的收敛曲线图。可以看出IAGA对比SACPMDE校准曲线尾部最窄，多次重复试验均收敛到近似同一值。

为了直观地看出算法校准收敛稳定性，量化上述校准曲线尾部的宽度，即目标函数的离散程度，如图5所示为不同地区不同品种下IAGA、MECA、PSO、ALEMSPSO、DE、SACPMDE各算法在参数校准收敛后尾部目标函数值分布箱型图，可以看出，差分算法系列在各训练数据集上收敛后目标函数的变化区间都接近于0（箱型图箱体的高度及离散点的分散情况直观对比可得）。在宜兴武育粳训练数据集上各算法参数校准收敛后目标函数值的变化区间大小分别为2.12、0.90、1.06、0.99、0.15、0.15。在兴化武育粳3号训练数据集上目标函数值变化区间大小分别为1.22、1.22、2.03、1.97、0、0，在高要雪花粘训练数据集上为0.71、0.80、1.43、1.38、0.10、0.10，在高要芦丝占上为0.34、0.39、0.79、0.69、0.11、0.11，在两优培九训练数据集上为5.67、2.42、4.14、3.84、0.16、0，表明差分算法系列在RiceGrow物候期模型参数校准问题上多次收敛到同一目标函数值算法稳定鲁棒性较好。

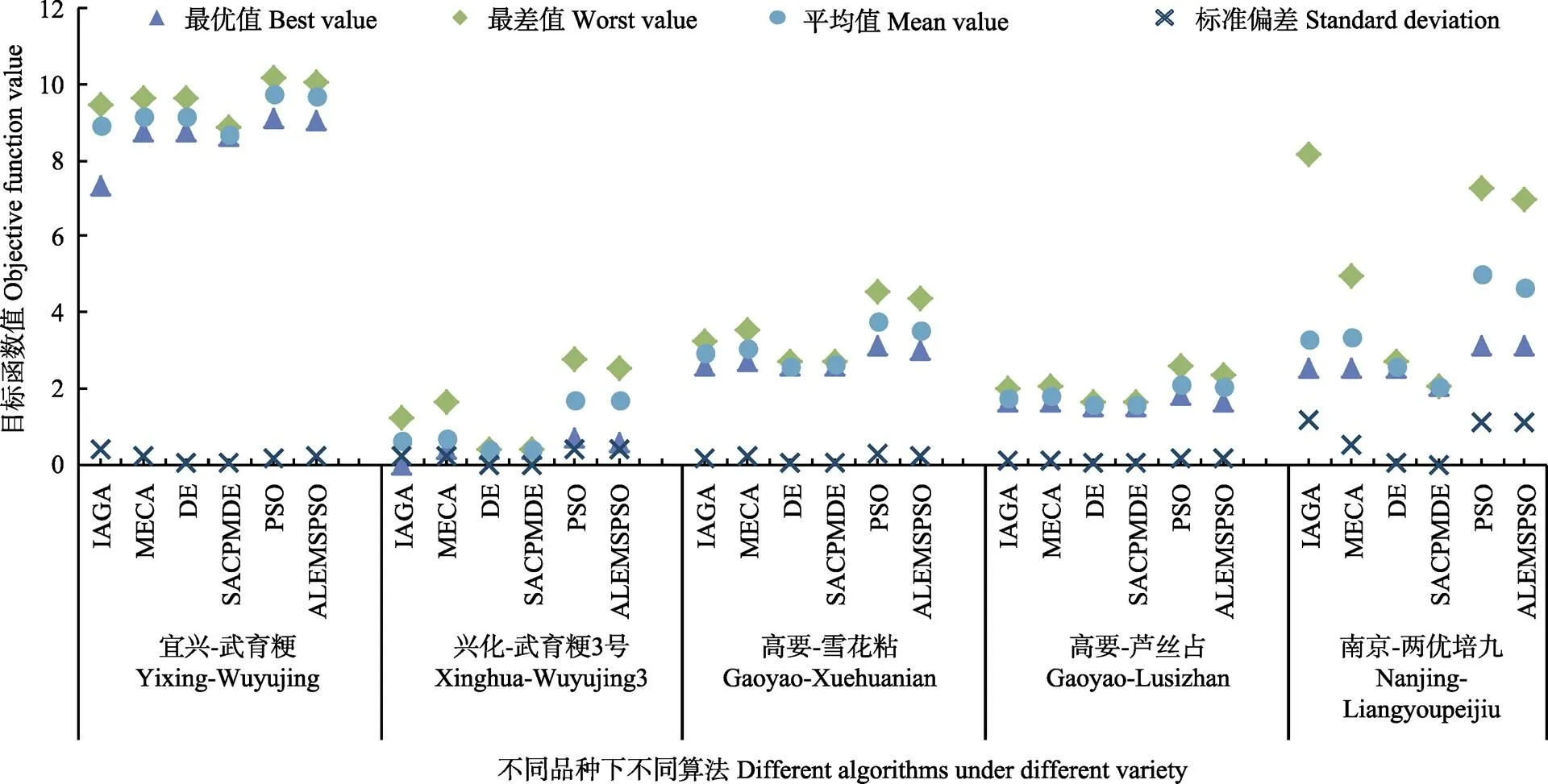
图3 不同生态点不同品种数据下基于不同进化算法的RiceGrow物候期模型参数校准的目标函数值

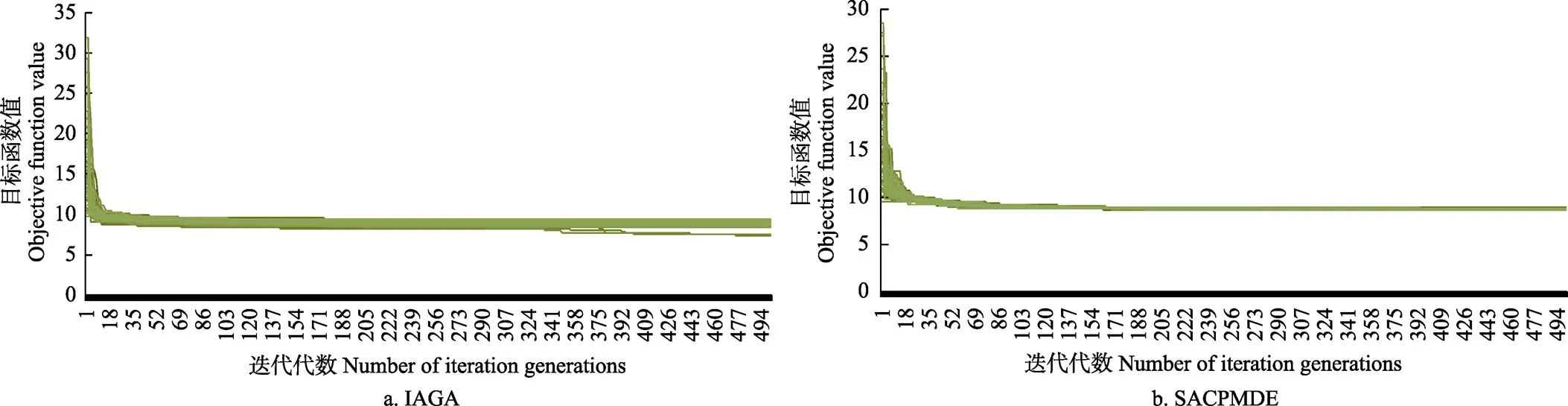
图4 宜兴地区武育粳品种数据在不同进化算法下对RiceGrow物候期模型参数校准重复100次试验收敛曲线

图5 不同进化算法在不同品种下对RiceGrow物候期模型参数校准重复100次试验收敛稳定性箱型图

从上述分析可以看出，SACPMDE和DE算法对RiceGrow物候期模型参数校准结果最准确，算法稳定鲁棒性最好，而DE的算法参数是由经验确定，也可以达到较好的校准精度，但是同SACPMDE算法相比两者在达到近似校准精度时，SACPMDE比DE收敛的速度平均快117代。

3 讨 论

差分进化算法自身参数主要涉及种群规模、缩放因子F和交叉概率CR。本文采用的自适应控制参数改进差分进化算法（SACPMDE），其缩放因子、交叉概率都是随其适应度的变化而动态的调整。种群大小对模型参数校准也会有影响，设置种群大小为50、150、150和200不同梯度值，分别重复试验100次得到参数校准结果，如图6所示。种群大小为100以后， RMSE/NRMSE/MAD/2变化分别在0～0.3 d，0～0.2%，0～0.3 d，0～0.02之间，变化幅度很小。而SACPMDE算法在各数据集上随种群规模50/100/150/200的收敛代数分别为342/354/367/ 356、120/106/99/92、192/186/191/180、192/200/215/234和244/121/235/219。随着种群大小的增加，其收敛代数也并没有有所减少，反而在宜兴、高要、南京数据集上因种群大小的增大，导致算法收敛代数增加，增加了算法时间和空间复杂度。由此可见，本研究选择种群大小为100是合理的。

图6 不同生态点不同品种下SACPMDE的不同种群大小的参数校准评价指标

本文以RiceGrow物候期模型为应用对象，验证了Zúñiga等[17]对于DE算法在作物模型参数校准问题上更为有效的结论。从建模原理上讲，稻麦等C3作物的生长发育过程及其与环境的关系、模型构建过程等都有相似之处，不同作物生长模拟模型的构建是以相似的生理生态过程为基础，采用不同的数学计算方法的集合，它们使用的模式、模拟方法以及细化程度虽各不相同，但关键概念及过程相似[31]。其计算过程具有非凸、非线性特点，适合于用全局启发式优化算法求解全局近似解。由此分析可知，理论上看，差分进化算法在C3作物的各类物候期模型品种参数校准应用上也具有适应性，但是还需进一步试验验证。此外，由于物候期模型品种参数之间存在一定程度的制约关系，不可避免的会出现“异参同效”现象，对“异参同效”结果的处理也是下一步研究的重要内容。

4 结 论

本研究以RiceGrow物候期模型为应用对象，通过试验研究，量化分析了差分进化系列算法、协同进化遗传算法（IAGA和MECA）、粒子群算法系列（PSO和ALEMSPSO）共3类进化算法在水稻物候期模型参数自动校准应用中的精确度、收敛速度及稳定鲁棒性。研究发现：基于参数自适应改进差分进化算法（SACPMDE）校准作物物候期模型品种参数具有更好的准确性、收敛速度和稳定性。

1）应用SACPMDE算法进行模型参数校准时，该算法在校准精度方面较其他进化算法表现好，同时算法参数易于确定。该算法交叉概率因子和缩放因子随进化过程个体适应度的变化而自适应的调节，避免了标准DE算法参数值的确定对优化问题的依赖性，提高了算法的鲁棒性和自适应性。利用武育粳等5个品种在江苏宜兴、兴化和广东高要等地的多年不同品种不同地点的田间试验资料试验验证表明：利用SACPMDE校准后的生育期模型在拔节期、抽穗期、成熟期的RMSE为1.7～4.6 d、NRMSE为1.8%~5.8%、MAD为1.4～3.3 d、2为 0.977～0.997，较其他类型进化算法的校准精度高。

2）应用SACPMDE算法进行模型参数校准时，该算法在收敛速度及稳定鲁棒性方面较其他进化算法表现好。在达到相似校准精度时，SACPMDE比DE收敛的速度平均快117代。基于SACPMDE的作物物候期模型参数校准试验重复100次的目标函数标准偏差趋近于0，同时得到的多套品种参数值标准偏差也较小，表明算法稳定鲁棒性好。

[1] Fukui S, Ishigooka Y, Kuwagata T, et al. A methodology for estimating phenological parameters of rice cultivars utilizing data from common variety trials[J]. Journal of Agricultural Meteorology, 2015, 71(2): 77－89

[2] Confalonieri R, Bregaglio S, Acutis M. Quantifying uncertainty in crop model predictions due to the uncertainty in the observations used for calibration[J]. Ecological Modelling, 2016, 328: 72－77.

[3] Wang C, Duan Q, Tong C H, et al. A GUI platform for uncertainty quantification of complex dynamical models[J]. Environmental Modelling & Software, 2016, 76(C): 1－12.

[4] Kersebaum K C, Boote K J, Jorgenson J S, et al. Analysis and classification of data sets for calibration and validation of agro-ecosystem models[J]. Environmental Modelling & Software, 2015, 72(C): 402－417.

[5] 李明亮. 基于贝叶斯统计的水文模型不确定性研究[D].北京：清华大学，2012. Li Mingliang. Research on Uncertainty of Hydrological Model Based on Bayesian Statistics[D]. Beijing: Tsinghua University, 2012. (in Chinese with English abstract)

[6] Wang J, Li X, Fang F, et al. Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method[J]. Environmental Modelling & Software, 2013, 48(5): 171－182.

[7] Vazquez-Cruz M A, Guzman-Cruz R, Lopez-Cruz I L, et al. Global sensitivity analysis by means of EFAST and Sobol’ methods and calibration of reduced state-variable TOMGRO model using genetic algorithms[J]. Computers & Electronics in Agriculture, 2014, 100(100): 1－12.

[8] Tatsumi K. Effects of automatic multi-objective optimization of crop models on corn yield reproducibility in the U.S.A[J]. Ecological Modelling, 2016, 322(3): 124－137.

[9] Tan J, Cui Y, Luo Y. Global sensitivity analysis of outputs over rice-growth process in ORYZA model[J]. Environmental Modelling & Software, 2016, 83:36－46.

[10] 何亮，侯英雨，赵刚，等. 基于全局敏感性分析和贝叶斯方法的WOFOST作物模型参数优化[J]. 农业工程学报，2016，32(2)：169－179. He Liang, Hou Yingyu, Zhao Gang, et al. Parameters optimization of WOFOST model by integration of global sensitivity analysis and Bayesian calibration method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 169－179. (in Chinese with English abstract)

[11] Xi Maolong, Lu Dan, Qi Zhiming, et al. Parameter estimation in RZWQM surrogate model using random drift particle swarm optimization algorithm[J]. Computer Engineering & Applications, 2016, 52(20): 35－41.

[12] Sun M, Zhang X, Huo Z, et al. Uncertainty and sensitivity assessments of an agricultural–hydrological model (RZWQM2) using the GLUE method[J]. Journal of Hydrology, 2016, 534: 19－30.

[13] Dumont B, Leemans V, Mansouri M, et al. Parameter identification of the STICS crop model, using an accelerated formal MCMC approach[J]. Environmental Modelling & Software, 2014, 52(12): 121－135.

[14] Kim K, Whelan G, Purucker S T, et al. Rainfall–runoff model parameter estimation and uncertainty evaluation on small plots[J]. Hydrological Processes, 2015, 28(20): 5220－5235.

[15] 梁浩，胡克林，李保国. 基于PEST的土壤-作物系统模型参数优化及灵敏度分析[J]. 农业工程学报，2016，32(3)： 78－85. Liang Hao, Hu Kelin, Li Baoguo. Parameter optimization and sensitivity analysis of soil-crop system model using PEST[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(3): 78－85. (in Chinese with English abstract)

[16] Wallach D, Makowski D, Jones J W, et al. Working with Dynamic Crop Models (Second Edition)[M]. Longdon: Elsevier, 2014.

[17] Zúñiga E C T, Cruz I L L, García A R. Parameter estimation for crop growth model using evolutionary and bio-inspired algorithms[J]. Applied Soft Computing, 2014, 23: 474－482.

[18] Soundharajan B, Sudheer K P. Sensitivity analysis and auto- calibration of ORYZA2000 using simulation-optimization framework[J]. Paddy & Water Environment, 2013, 11(1/ 2/3/4): 59－71.

[19] 庄嘉祥，姜海燕，刘蕾蕾，等. 基于个体优势遗传算法的水稻物候期模型参数优化[J]. 中国农业科学，2013，46(11)：2220－2231. Zhuang Jiaxiang, Jiang Haiyan, Liu Leilei, et al. Parameters optimization of rice development stages model based on individual advantages genetic algorithm[J]. Scientia Agricultura Sinica, 2013, 46(11): 2220－2231. (in Chinese with English abstract)

[20] Pabico J P, Hoogenboom G, Mcclendon R W. Determination of cultivar coefficients of crop models using a genetic algorithm: A conceptual framework[J]. Transactions of the ASAE, 1999, 42(1): 223－232.

[21] Chalabi Z, Zhou W. Optimal control methods for agricultural systems[J]. Acta Horticulturae, 1996, 406(406): 221－227.

[22] Tang L, Zhu Y, Hannaway D, et al. RiceGrow: A rice growth and productivity model[J]. NJAS-Wageningen Journal of Life Sciences, 2011, 57(1): 83－92.

[23] Storn R. On the usage of differential evolution for function optimization[C]//Fuzzy Information Processing Society, 1996. NAFIPS. 1996 Biennial Conference of the North American. IEEE Xplore, 1996:519‒523.

[24] Vesterstrom J, Thomsen R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems[C]//Evolutionary Computation, 2004. CEC2004. Congress on. IEEE, 2004: 1980－1987.

[25] Wu L, Wang Y, Zhou S, et al. Self-adapting control parameters modified differential evolution for trajectory planning of manipulators[J]. Journal of Control Theory and Applications, 2007, 5(4): 365－373.

[26] Kobayashi K, Salam M U. Comparing simulated and measured values using mean squared deviation and its components[J]. Agronomy Journal, 2000, 92(2): 345－352.

[27] Gauch H G, Hwang J T G, Fick G W. Model evaluation by comparison of model-based predictions and measured values[J]. Agronomy Journal, 2003, 95(6): 1442－1446.

[28] 慕彩红，焦李成，刘逸，等. M-精英协同进化数值优化算法[J]. 软件学报，2009，20(11)：2925－2938.Mu Caihong, Jiao Licheng, Liu Yi, et al. M-elite coevolutionary algorithm for numerical optimization[J]. Journal of Software,2009, 20(11): 2925－2938. (in Chinese with English abstract)

[29] Kennedy J, Eberhart R. Particle swarm optimization[C]// Icnn'95 - International Conference on Neural Networks. IEEE, 2002:1942‒1948.

[30] 王芳芳，姜海燕，郭小清，等. 基于自主学习和精英群的多子群粒子群算法[J]. 控制与决策，2014，29(11)：2034－2040.Wang Fangfang, Jiang Haiyan, Guo Xiaoqing, et al. Multi-swarm particle swarm optimization based on autonomic learning and elite swarm[J]. Control & Decision, 2014, 29(11): 2034－2040. (in Chinese with English abstract)

[31] 姜海燕，朱艳，汤亮，等. 基于本体的作物系统模拟框架构建研究[J]. 中国农业科学，2009，42(4)：1207－1214.Jiang Haiyan, Zhu Yan, Tang Liang, et al. Study on ontology- based framework of crop system simulation[J]. Scientia Agricultura Sinica, 2009, 42(4): 1207－1214. (in Chinese with English abstract)

Automatic calibration of parameters for crop phenological predicting model based on adaptive differential evolution algorithm

Jiang Haiyan1,2, Zhao Kongnuan1, Tang liang2, Li Yushuo1, Yang Hua1

(1.210095,;2.210095,)

Evolutionary algorithms have been widely used in the field of crop model parameter calibration. Since the crop model structure includes multiple sets of ordinary differential equations with nonlinear, discontinuous and multi-peak characteristics, it is especially important to select appropriate evolutionary algorithms based on crop model characteristics. At the same time, the parameters of the evolutionary algorithm have a great influence on the performance of the algorithm. These parameter selections are often based on experience, which increases the uncertainty of the optimization algorithm in the model parameters calibration process . This article was targeted on problem of selection and parameter uncertainty of the evolutionary algorithm applied to the crop phenological model parameter correction quasi-process . In this paper, the rice RiceGrow phenological predicting model was applied to compare the correction accuracy, convergence speed and stability robustness of 3-tyepe evolutionary algorithms in application. Comparison algorithms included differential evolution series algorithms (standard differential evolution algorithm(DE) and adaptive control parameters modified differential evolution algorithm(ACPMDE)), co-evolutionary genetic algorithm series (individual advantage genetic algorithm, M-elite co-evolution algorithm) and particle swarm optimization series (standard particle swarm optimization, multi-subgroup particle swarm optimization based on autonomous learning and elite groups). Using the multi-year field experiment data of 5 species of Wuyujing and Xuehuanian in different ecological points such as Yixing, Xinghua in Jiangsu province and Gaoyao in Guangdong province, the accuracy, convergence rate and stability robustness of the automatic correction of the model parameters was quantitatively analyzed with different evolutionary algorithms. The results showed that: 1) the correction accuracy of the model parameters of the model with adaptive control parameters modified differential evolution algorithm was higher than other algorithms, and the parameters of the algorithm were easier to determine. The cross-probability factor and scaling factor of the algorithm were adaptively adjusted with the individual fitness function during the evolution process, in which the dependence of the standard DE algorithm parameters on the optimization problem was avoided and the robustness of the algorithm was improved. The RMSE(root mean square error) between the predicted and observed values of jointing, heading and maturity stage was 1.7-4.6 days; The normalized root mean spuare error was 1.8%-5.8%; MAD(mean absolute difference) was 1.4-3.3 days, and determination coefficient2was 0.977-0.997, which was 0.634 days, 0.608%,0.453 days, 0.09% smaller than co-evolutionary genetic algorithm series, 1.399 days, 1.35%, 1.039 days,0.23% smaller than PSO series. 2) Applying adaptive control parameters to improve the differential evolution algorithm showed good convergence speed and stable robustness on the phenomenological model parameter correction. The standard deviation of the objective function value of 100 times repeated calibration experiment approached 0, and the standard deviation of the variety parameter values obtained by each correction was also smaller than other algorithms. With the same accuracy, the adaptive control parameter modified differential evolution algorithm converges 117 iterations faster than the standard differential evolution algorithm. The research showed that the automatic correction quasi-method of crop phenological model parameters based on adaptive control parameters modified differential evolution algorithm had good accuracy and stability and was suitable for practical application.

crops; models; meteorology; adaptive control parameters; differential evolution; evolutionary algorithm; phenologicalmodel; parameter calibration

10.11975/j.issn.1002-6819.2018.21.021

S126; TP391

A

1002-6819(2018)-21-0176-09

2018-06-05

2018-10-10

国家自然科学基金面上项目（31872847）；江苏省农业科技自主创新资金项目（CX(16)1038）；江苏省研究生培养创新工程项目（SJCX17_0198）；南京市农业科技产学研合作示范项目（2017RHJD06）；江苏省渔业科技类项目（D2017-1-1）

姜海燕，女，浙江临安人，博士，教授，研究方向：作物系统建模、智能计算。Email：jianghy@njau.edu.cn

姜海燕，赵空暖，汤 亮，李玉硕，杨 华.基于自适应差分进化算法的水稻物候期预测模型参数自动校正[J]. 农业工程学报，2018，34(21)：176－184. doi：10.11975/j.issn.1002-6819.2018.21.021 http://www.tcsae.org

Jiang Haiyan, Zhao Kongnuan, Tang Liang, Li Yushuo, Yang Hua. Automatic calibration of parameters for crop phenological predicting model based on adaptive differential evolution algorithm [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(21): 176－184. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.21.021 http://www.tcsae.org