轴向运动热弹耦合楔形梁的振动特性

郭旭侠，薛晓飞

(宝鸡文理学院，陕西 宝鸡 721013)

0 引 言

梁作为实际工程中的基本构件，被大量的用于各类结构中。变截面梁具有质量分布合理、力学性能优异的特点，被广泛应用于航空航天，机械、建筑等领域。变截面梁引起有质量分布合理等优异的力学性能，被广泛的应用于航空航天，机械、建筑等领域[1-2]。Abrate[3]采用位移变分法研究了截面线性变化的变截面悬臂梁的自由振动。葛仁余[4-5]等运用插值矩阵法一次性计算出轴向功能梯度变截面梁各阶振动固有频率，同时获取了相应的振型参数。刘雷[6]采用半解析法计算了一类变截面梁的固有频率和振型，通过与有限元法的计算结果比较说明了半解析解的精确性。上述研究均没有考虑温度变化对系统稳定性的影响，温度场与位移场的耦合作用增加了方程的求解难度。分析了轴向运动变截面梁在热弹耦合作用下的振动特性。

1 建立数学模型

建立图1所示为楔形截面轴向运动弹性梁，该梁沿x轴的运动速度为v。梁沿x方向的长度为L，宽度为b，材料密度为ρ，弹性模量为E。假设梁的初始温度是τ0=τ(x,z,t0)，任一瞬时t梁的温度是τ1=τ1(x,z,t)，则梁的温度变化为T=τ1-τ0。在x=0及x=L处梁的高度分别为h1、h2，设梁的高度沿x方向的变化规律满足：

(1)

图1 楔形截面热弹耦合轴向运动梁

楔形梁的横截面弯矩M为：

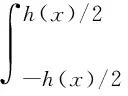
(2)

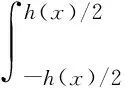
等截面轴向运动梁的运动微分方程是：

(3)

式中：A=bh(x)为梁的横截面面积。

将式(2)代入式(3)得楔形截面梁的热弹运动微分方程是[7]：

(4)

梁的热传导方程是[8]：

(5)

将以下无量纲量：

(6)

分别代入式(4)和式(5)中，得：

(7)

设方程(7)的解：

(8)

将式(8)代入式(7)，得:

求解方程(10)进行，得:

(11)

将方程(11)代入式(9)得:

(12)

梁在两端恒温条件下的边界条件为:

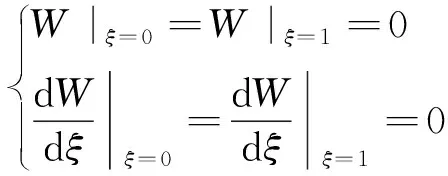
(13)

2 算例分析

参照微分求积法的计算步骤与求解原理[9-10]，方程 (12)可离散为以下形式:

(14)

边界条件式(13)的微分求积形式：

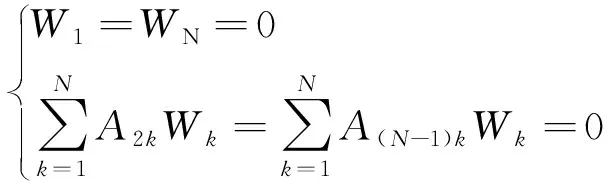
(15)

将式(14)和式(15)写成矩阵形式，即：

(16)

式中：下标d为边界上的量；e为非边界上的量{yd}、{ye}如下：

(17)

由式(15)消去{yd}得:

{ω2[I]+ω[G]+[K]}{Wk}={0}

(18)

矩阵[K]、[G]和[I]中含有耦合项系数及无量纲运动速度等参数。方程(18)构成了广义特征值问题。因此，热弹耦合轴向运动梁的特征方程是:

|ω2[I]+ω[G]+[K]|=0

(19)

表1 楔形梁前三阶固有频率的本文解与文献[11]解的比较

图2 无量纲速度c与无量纲复频率ω关系曲线

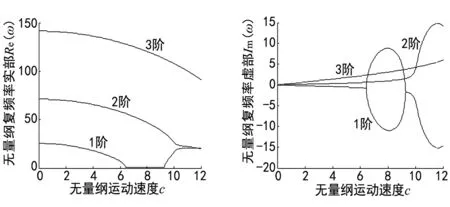
图3 无量纲速度c与无量纲复频率ω关系曲线

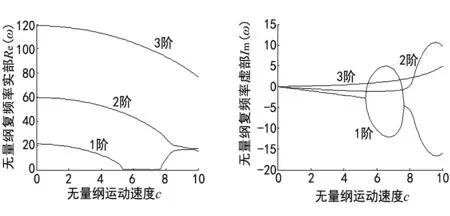
图4 无量纲速度c与无量纲复频率ω关系曲线

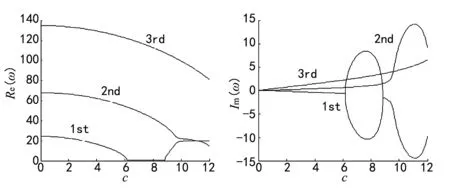
图5 无量纲速度c与无量纲复频率ω关系 曲线

通过对三图进行比较分析发现，当λ分别取0，0.2和0.3时，对应的第一阶模态发散失稳的无量纲轴向运动速度临界值分别取c=6.159，c=6.731，c=7.061，由此得出，楔形变截面轴向运动梁第一阶模态处于发散失稳状态的无量纲轴向运动速度临界值会随热弹耦合因子的变大而变大。

图6 无量纲速度c与无量纲复频率ω关系 曲线

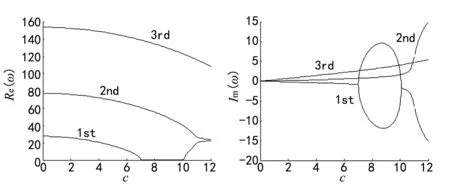
图7 无量纲速度c与无量纲复频率ω关系 曲线

3 结 论

通过算例分析可以看出微分求积法可以满足计算要求，过程简便计算机易于操作。数值结果表明随着无量纲速速的提高，楔形梁的前三阶模态复频率的实部都随着减小。当楔形梁的梁高比减小时，梁发散失稳的临界速度随之减小，单一模态颤振的临界速度变化趋势相同，只是梁的失稳类型没有发生改变。考虑热弹耦合效应时梁的前三阶固有频率与不考虑热弹耦合效应时相比，梁的前三阶固有频率均变大。