仿落猫机器人嵌入式控制系统设计

2018-11-05叶晓东张鹏万

新技术新工艺 2018年10期

王涛，叶晓东，李露，张鹏万

(1.中国科学技术大学精密机械与精密仪器系，安徽合肥 230026；2.中国科学院合肥物质科学研究院先进制造技术研究所，江苏常州 213164)

机器人作为一门快速发展的学科，涉及到仿生学、机械、电子以及控制等多个学科，是20世纪以来人类最重要的成就之一。当代机器人的研究与应用已从结构环境下的定点作业拓展到星际探测、地质勘探、灾难救援、反恐防暴等非结构环境下的自主作业领域。腿式机器人相对于轮式和履带式机器人在非结构环境中有优势，但运动环境对腿式机器人仍有诸多限制。为了进一步扩大腿式机器人应用场合，如外星球探测器着陆、深井救援机器人着陆以及高空救援机器人着陆等，需要解决腿式机器人从空中无意跌落或被空投时的安全着陆问题；因此，研究机器人依靠自身的机械、控制系统实现任意姿态跌落的安全着陆问题尤为重要。

当一只猫从高空坠落时，它总能通过自身的调整，安全的四脚着地。为揭示猫在不违背角动量守恒的情况下空中自动翻正的力学原理，很多科学家提出了各种假设，有四肢开合论、转尾巴论、绕双轴转动论和弯腰论等。其中，被广泛认可的是由Kane和Scher提出的弯腰论[1]，他们将猫简化为一个以腰部为顶点的2个轴对称刚体组成的双刚体模型，分别代表猫的前半身和后半身，解释了猫的转体运动。他们认为，在猫下落过程中，当系统总角动量为零时，落猫轨迹规划问题等价于非完整运动规划问题，因此，落猫问题成为一个典型的非完整运动问题。由于系统的自由度多于独立控制变量，所以，即使知道系统的动力学方程，也没有唯一的方法处理非完整系统，因此，落猫控制问题变得非常困难。Iwai等[2]改进了Kane-Scher模型，通过移除前后体之间不可扭转这个条件，释放了1个自由度，并提出了一个可以扭转的Kane-Scher模型(Twisted Kane-Scher Model)。中野太智等[3]通过利用路径积分增强式学习算法，研究了可扭转的Kane-Scher模型姿态调整的轨迹规划问题，得到3个不同初始状态下的下落姿态角轨迹，不过得到的结果普遍存在超调。

常见的小型腿式机器人的控制系统通常使用DSP系列控制器[4]、Atmel AVR系列微控制器[5]。该仿落猫机器人由3个AX-12A数字舵机控制，既要保证仿落猫机器人能够进行自由的翻转运动，同时还要采集和处理传感器、陀螺仪等信息，实时反馈传感器数据来用于控制机身的姿态调整，使其在非结构环境中具有很好的适应和决策能力，这些需求增加了难度；因而，只有设计轻便、工作频率更高和处理能力更强的控制系统才能满足要求。具有高性能的ARM Cortex-M3 32位的RISC内核的嵌入式芯片STM32F103C6T6，以其功耗低，工作频率可高达72 MHz，较大的Flash和高速存储器，以及丰富的接口，最大程度地满足了仿落猫机器人运动控制系统的要求[6]。

1 仿落猫机器人动力学模型

应用SolidWorks软件设计的仿落猫机器人的虚拟样机模型如图1所示。该机器人包含9个自由度，由3个舵机控制。

图1 仿落猫机器人虚拟样机模型

从图1中可以看出，该虚拟样机主要由仿落猫机器人的前半身、后半身、舵机、配重块以及仿落猫机器人四肢所组成。其中，舵机是用来对仿落猫机器人自由下落过程中姿态调整进行控制，配重块的作用是保持仿落猫机器人在空中进行翻正动作时的身体平衡。需要指出的是，为了尽量减少仿落猫机器人的体积以及其质量，样机中机器人的前后半身用质量的扁平体代替，之所以未用圆柱体是为了减轻机器人的质量。

在猫的下落过程中，脊柱依次向各个方向弯曲，猫的前半身做一轮弯腰运动，整个身子就向相反方向旋转180°，达到翻正目的[7]。仿照落猫翻正原理，本文采用可扭转的Kane-Scher模型建立仿落猫机器人的动力学模型(见图2)。B1和B2分别代表机器人的前半身和后半身。

图2 仿落猫机器人的数学模型

在图2中，O为机器人前后体的联结处，Oc为整个机器人的质心，OX1为从O点指向头部的中心轴，OX2为从尾部指向O点的中心轴，Ψ为前半身与后半身之间的夹角，θ1、θ2为前后体分别绕OX1和OX2的转动角度，χ1、χ2、χ3整体分别绕oe1、oe2、oe3转动，可扭转的Kane-Scher模型的状态方程可以表述为：

2 仿落猫机器人控制系统

2.1 嵌入式总线控制系统

嵌入式总线控制系统主要用于信息的协调同行，笔者设计的嵌入式控制系统的驱动控制板与仿落猫机器人之间[8]，选择了STM32F103C6T6作为总线控制系统的主控芯片，总线控制系统主要包括串口模块、nRF24L01无线接收通信模块电路、复位模块和SWD模块(见图3)。

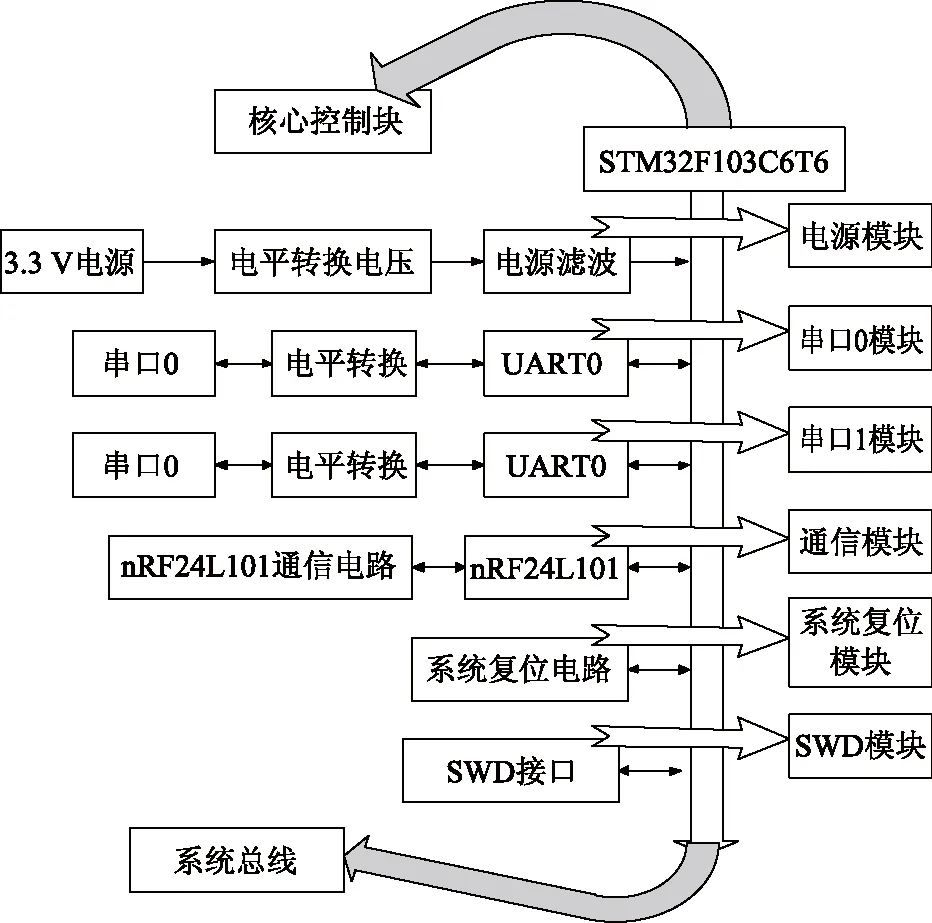
图3 嵌入式总线控制系统框图

2.2 控制系统硬件电路

控制系统硬件部分的电路分为电源部分、主控电路及其相应的外部连接电路，其中主控电路包含2个USART串口、8路A/D采集接口和1个SPI通信接口。主控电路对机器人进行集中控制，负责仿落猫机器人的舵机驱动，响应上位机控制信号。

控制系统部分的高性能控制芯片让机器人控制的实时性和可靠性显得更出色。主要控制系统部分的电路如图4所示。

图4 控制系统部分电路图

2.3 控制系统软件设计

软件控制流程(见图5)如下：首先，对系统进行初始化；然后，通过对传感器采集的信息进行实时监控来判断落猫机器人是否处于跌落状态，当机器人以不正确的姿态跌落时，便通过控制器和驱动器来控制电动机的转动，进而控制机器人空中姿态的调整；最后，对比传感器监测到的实时姿态角和期望姿态角，当实时姿态角等于期望姿态角时，说明空中姿态调整结束，机器人也已经实现了翻正，开始以正确的姿态准备着陆。在姿态调整的过程中，拟采用轨迹规划的方法进行运动控制，即首先通过最优化方法，获得落猫机器人自由下落过程中各个姿态角的最优化曲线，然后在控制器中写入所得数据，使控制电动机按照希望的速度运转，此时机器人可以按照预设的轨迹运动，最后实现翻正动作。

图5 软件控制流程图

3 仿真及试验分析

在MATLAB软件中利用Simulink工具箱进行仿落猫机器人轨迹规划仿真分析，根据仿落猫机器人的状态方程通过粒子群算法得到它的优化轨迹以及姿态角，并将得到的姿态角数据通过程序烧录到控制板中进行舵机的驱动控制。使仿落猫机器人按规划的轨迹进行空中自由翻转下落运动[9]。

针对该仿落猫机器人进行了轨迹规划，其中机器人轨迹规划仿真结果如图6所示，图6反映了力矩输入及各姿态角在翻转过程中的变化过程。

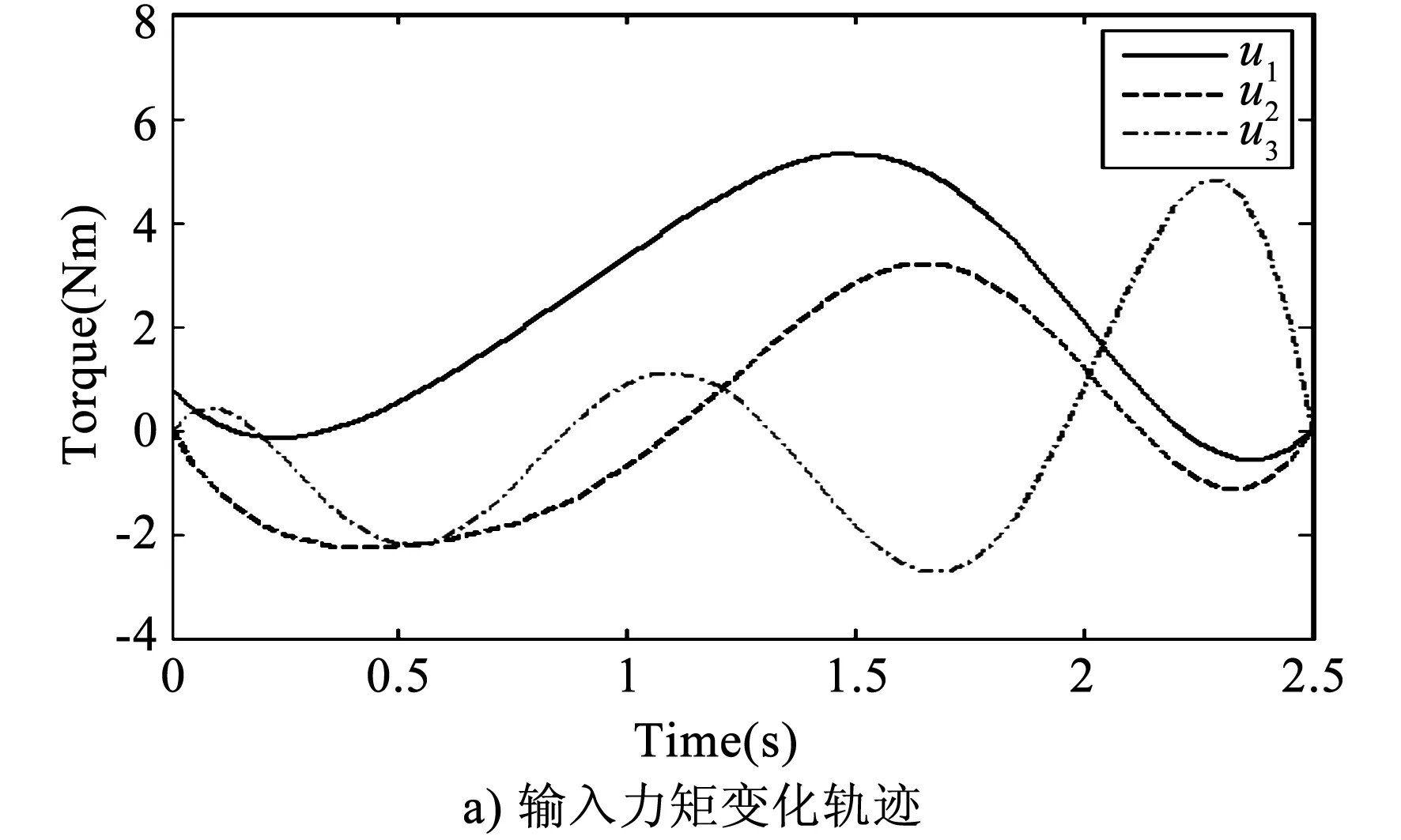
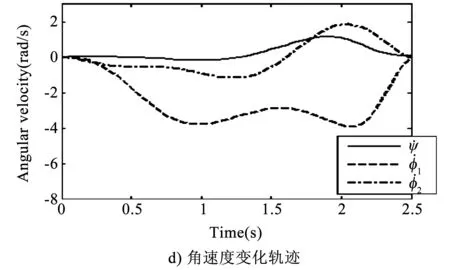
图6 机器人轨迹规划仿真结果图

图6a表示仿落猫机器人在自由下落的过程中，其嵌入式控制系统的控制输入力矩的输入轨迹，从图6a中可以看出，从开始到结束每条曲线变化平稳，两端控制输入力矩均为0，该曲线表示仿落猫机器人在下落初始瞬间相应的控制力矩输入为0，完成姿态调整后着陆瞬间的控制力矩输入也为0。图6b表示仿落猫机器人在下落过程中姿态角的变化曲线，从图6b中可以得知，仿落猫机器人下落过程中旋转角θ1和θ2从0光滑地变化到-2π，且仿落猫机器人的旋转角θ1和θ2不同步，意味着仿落猫机器人前后体之间在自由下落的过程中实现了相对扭转，机器人的脊椎弯曲角Ψ从下落瞬间的初始姿态角7π/12缓慢地变化到期望姿态角5π/6，同时也表明脊椎弯曲幅度较小。图6c表示仿落猫机器人的回转角的优化轨迹，其中χ2从0变化到π，χ1和χ3在整个下落过程中基本上为0并保持不变，这就意味着仿落猫机器人在空中姿态调整后翻正成功，并且机器人在进行姿态调整的整个过程进行平稳。图6d表示仿落猫机器人角速度的轨迹变化曲线，从图6d中可以得知，在仿落猫机器人下落过程中，一直到完成翻正动作安全着陆，各个角速度值的变化从0到0，且波动较小，符合角动量守恒定律，并且也符合工程实际。

仿落猫机器人自由翻转下落的实物图如图7所示。

图7 仿落猫机器人实物样机

下述试验仿照猫在空中下落的情形，使仿落猫机器人在一定的高度四肢朝上，然后将其松开使其形成自由下落的状态，也就是进行仿落猫机器人的自由落体试验。将轨迹优化所得数据输入设计的机器人控制器中，设置终止时间为t=2.5 s，并应用Keil uVision5软件将所编写的控制程序烧进去，同时，应用keil软件进行同步控制，开始仿落猫机器人的自由落体试验，并用高速相机拍摄试验过程。通过整理高速相机拍摄结果，可以得到仿落猫机器人的自由落体试验的结果如图8所示。通过多次试验，所设计的嵌入式控制系统能较为精确地控制仿落猫机器人运动，实现空中翻转。