ARTIVA在时间序列基因表达数据网络构建中的应用*
2018-11-05哈尔滨医科大学卫生统计学教研室150081
哈尔滨医科大学卫生统计学教研室(150081)
刘会娟 侯 艳 李 康△
【提 要】 目的 探讨时间序列基因表达数据网络构建的ARTIVA模型与方法。方法 通过实例研究ARTIVA模型构建网络的效果。结果 实例分析表明,ARTIVA模型对时间序列数据具有良好的适应性,在具有3个时间点和9个时间点两种情况下,ARTIVA模型均能准确地模拟生物网络,并且能识别网络结构的动态变化过程。结论 ARTIVA模型适用于时间序列基因表达数据网络构建,具有较高的实用价值。
基于时间序列(time series)实验的基因表达数据,可以反映生物体在细胞循环、代谢等诸多生理过程中基因表达随时间推移发生的变化。基于时间序列基因表达数据的基因调控网络模型有多种,如时序布尔网络模型[1]、微分方程模型[2]、基于信息理论的互信息关联模型[3]以及动态贝叶斯网络方法[4]等。其中,时序布尔网络模型将基因表达值切割为0-1取值,相对其他方法会损失一定的信息。微分方程对数据要求较高,对当前信噪比低、测量噪声大的微阵列数据适应性较差,而且模型参数估计困难。多项研究表明,在分析时间序列基因表达数据时,动态贝叶斯网络方法可能是揭示复杂生物调控网络的最佳方法[5-6]。
本文将简要介绍时变向量自回归模型(autoregressive time varying models,ARTIVA)[7],并将其应用于时间序列基因表达数据构建基因调控网络,通过实际数据的分析,探索该模型构建网络的适用性。
原理与方法
1.ARTIVA网络模型
ARTIVA网络模型的基本思想是通过动态贝叶斯网络(dynamic bayesian network,DBN)描述基因间的调控关系,并通过可逆跳马尔科夫链蒙特卡洛方法(reversible jump Markov chain Monte Carlo,RJMCMC)推断网络拓扑结构以及网络结构发生改变的时间。
(1)基础ARTIVA网络模型
设有p个基因,测量T个时间点的基因表达数据X={Xi(t);1≤i≤p,1≤t≤T},则t时刻的基因表达X(t)={X1(t),…,Xp(t);1≤i≤p,1≤t≤T}可以通过一个一阶向量自回归过程表示:
X(t)=A(t)X(t-1)+B(t)+ε(t),
ε(t)~N(0,σij(t)),t≥2
(1)
即:
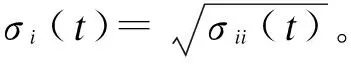
参数估计可以使用极大似然方法。其似然函数为
(2)
其中,n为第n个样本,总的样本量为N。
(2)具有时相的ARTIVA模型
ARTIVA网络模型假定网络结构有多个时变点(网络结构发生改变的时刻)。这些时变点将基因的表达分割成若干个时相,在同一时相内,调控关系保持不变。若有K(0≤K≤T-1)个时变点c={c0,c1,…,cK;cK≥2,K=0,1,…,K},模型服从一阶马尔科夫假定时,在时相c(h-1)与c(h)内,基因的表达X可以通过回归模型表示:
X(t)=A(h)X(t-1)+B(h)+ε(t),
ε(t)~N(0,σij(t)),t≥2
(3)
即:
其中,X(t-1)是基因在t-1时刻的表达水平,B(h)为在h时相内模型的常数项。总似然函数为
(5)
已知基因的表达X,给定模型参数(即时变点的个数与位置、父节点的个数及模型方差)的先验分布,可以通过RJMCMC方法估计上述模型参数的后验分布,具体实现可使用R软件包(https://CRAN.R-project.org/package=ARTIVA)。
实例分析
为研究ARTIVA方法在实际时间序列基因表达数据网络构建中的效果,选取两个实际数据进行分析。数据的基本情况如表1。
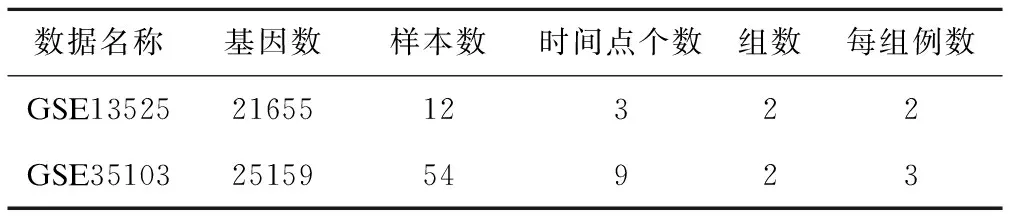
表1 两个时间序列基因表达数据的基本情况
1.GSE13525数据分析
GSE13525数据(https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE13525)来源于36M2卵巢癌细胞,分别用卡铂与对照试剂处理24小时,在处理结束后24小时、30小时和36小时检测mRNA,每个处理组分别有2个生物重复样本,得到共含12个样本、21655个基因的时间序列基因表达数据。对GSE13525数据进行数据清理,清除在GO数据库中无相应注释的探针,对注释相同的探针计算各个探针的四分位间距,保留四分位间距最大的探针进行变量筛选,得到组间差异基因103个,然后进行KEGG通路富集,得到32个通路,表2列出了通路富集的前10条通路。
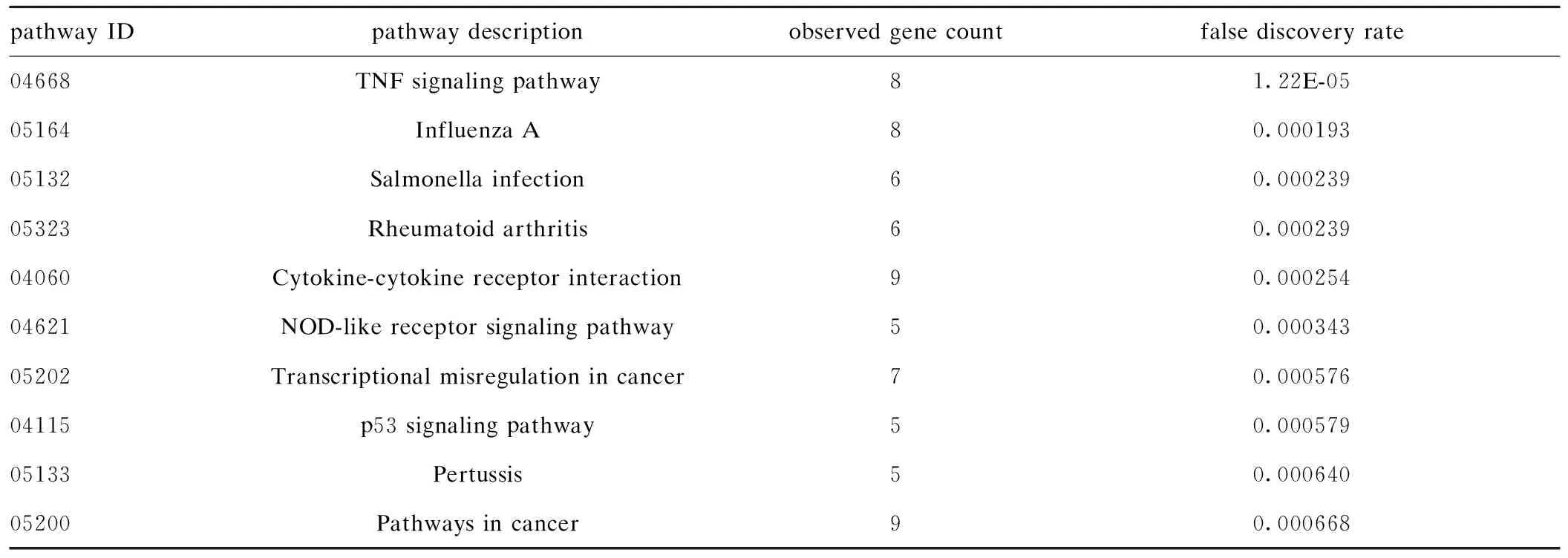
表2 GSE13525差异表达基因KEGG通路富集结果
表2的10条通路中,均是免疫相关通路,其中ID为04668、04060、04621和04115(p53信号通路)这4条通路均有与卵巢癌相关的报道。本文对ID为04668中的8个基因(BIRC3,CXCL2,CXCL3,EDN1,IL6,JAG1,JUN,TNFAIP3)构建网络,探索这8个基因间的调控关系。图1展示了这8个基因在STRING数据库中的相互作用关系,图2是本研究构建的基因调控网络。通过ARTIVA模型构建这8个基因的调控网络,发现IL6处于该网络的核心位置,与另7个基因的相互作用关系最密切,表明其可能在卵巢癌细胞凋亡过程中起关键作用。在STRING数据库中,不同颜色的边代表不同的相互作用关系。如紫色代表已有实验证实存在的调控关系,蓝色代表数据库中检索得到的调控关系,具体可参考STRING数据库官网(https://string-db.org/cgi/input.pl)。
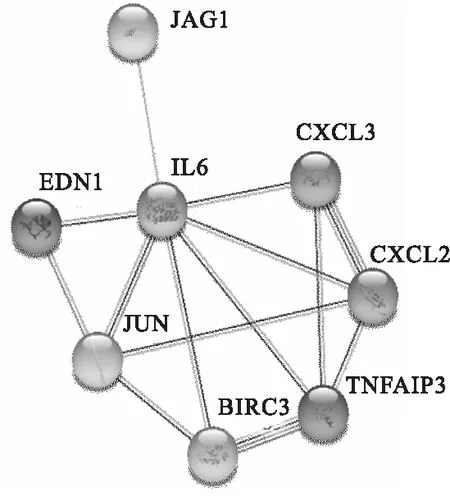
图1 STRING数据库中TNF通路基因互作网络
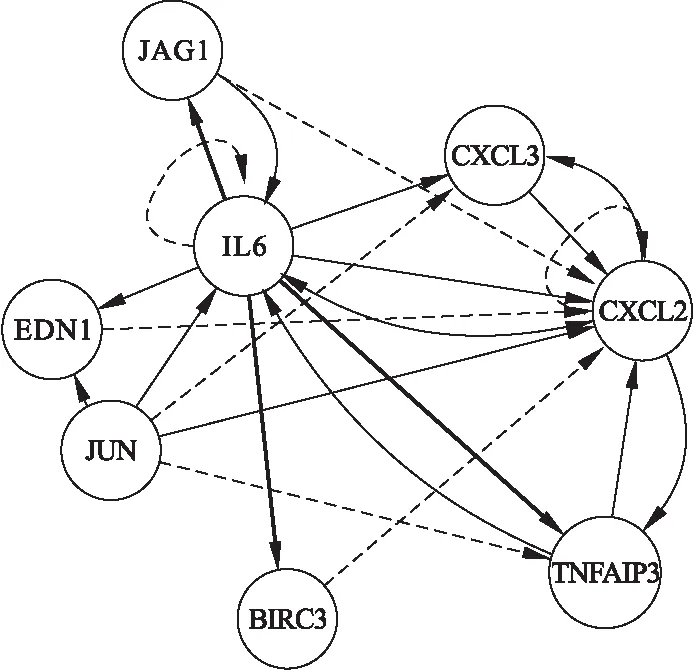
图2 TNF通路基因的ARTIVA 网络结构
在此实例应用中,由于只有3个时间点的基因表达数据,ARTIVA网络构建方法未能识别网络结构的动态变化。图2中红色实线标记的边表示在STRING数据库中得到验证的调控边,黑色虚线标记的边表示使用ARTIVA方法新发现的调控关系,ARITIVA网络中一共有23条边,其中16条在STRING数据库中得到了验证,有2条调控边是自调控关系,反映了普遍存在的反馈调节。边的粗细代表了调控关系后验概率的大小,后验概率越大边越粗。
2.GSE35103数据分析结果
GSE35103数据(https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi)来源于人脐带血CD4+ T细胞分化实验,分别用T细胞分化诱导剂(IL6,IL1b,TGFb)与对照试剂处理人脐带血CD4+ T细胞,在实验过程的不同时间点(0h,0.5h,1h,2h,4h,6h,12h,24h,48h,72h)检测实验组与对照组细胞的mRNA,每个处理组分别有3个生物重复样本,得到共含57个样本、25159个基因的时间序列基因表达数据。对GSE35103数据进行数据清理及变量筛选,过程如上述GSE13525,得到组间差异基因108个,然后进行KEGG通路富集得到68个通路。
其中Jak-STAT signaling pathway(fdr=9.85E-12)可以调节T细胞的免疫功能并且通过诱导细胞凋亡引起T细胞自我消亡,在T细胞分化过程中也扮演了重要角色。现对富集在通路中的12个差异基因(CCND1,CISH,CSF2,IL10,IL2RA,IL2RB,IL9,IRF9,SOCS1,SOCS3,STAT1,STAT3)构建网络。图3展示了这12个基因在STRING数据库中的相互作用关系,图4是使用ARTIVA方法构建的基因调控网络中所有的边,以及网络结构的动态变化。同样,红色实线标记的边表示在STRING数据库中能够验证的调控边,黑色虚线标记的边表示ARTIVA方法新发现的调控边(需要验证)。边的粗细代表了调控关系后验概率的大小,后验概率越大边越粗。ARTIVA网络结构中一共有23条边,其中16条得到了验证,另外7条调控边多为自调控关系。同时,ARTIVA方法将9个时间点自动分成了5个时相(时相1:0.5h~2h,时相2:2h~4h,时相3:4h~12h,时相4:12h~24h,时相5:24h~72h),在每个时相内网络结构保持稳定,在不同时相间网络结构随着时间推移发生变化,即各调控边的后验概率大小改变(图4)。图4中a-f分别对应整体ARTIVA 网络结构、时相1~时相5的网络结构。从图4可以看出:STAT1,SOCS3,IL2RA,CISH这几个节点具有较高的边密度,是T细胞分化过程中较为关键的调控点,可为T细胞的治疗性研究提供启示;网络的拓扑结构随着时间推移发生改变,在细胞分化的不同阶段,基因间的调控关系是动态变化的。这种变化体现在边的有无、调控边的方向以及强度上,为研究人员精确阻断细胞分化进程提供了依据。
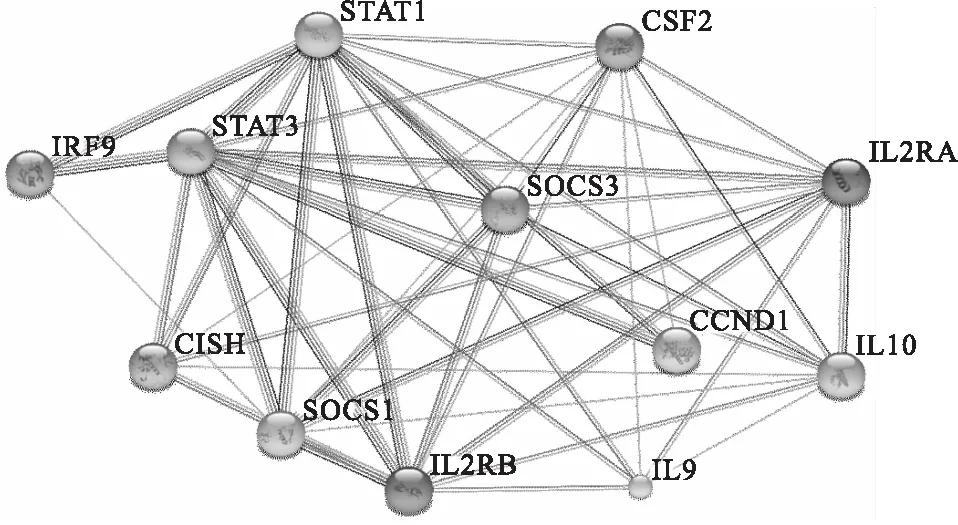
图3 STRING数据库中Jak-STAT通路基因互作网络
讨 论
1.动态贝叶斯网络(DBN)能够使用多个时间点的组学数据来构建网络,相对于断面数据,能够更好地揭示因果关系,处理反馈环路问题。本文介绍的ARTIVA模型是一种改进的DBN模型,不仅能够给出整体的网络结构,同时可以分别给出不同时相的网络结构,分析在不同时间段上网络调控关系的变化。另外,这种方法既可以用于二分类数据,也可以用于连续型数据。
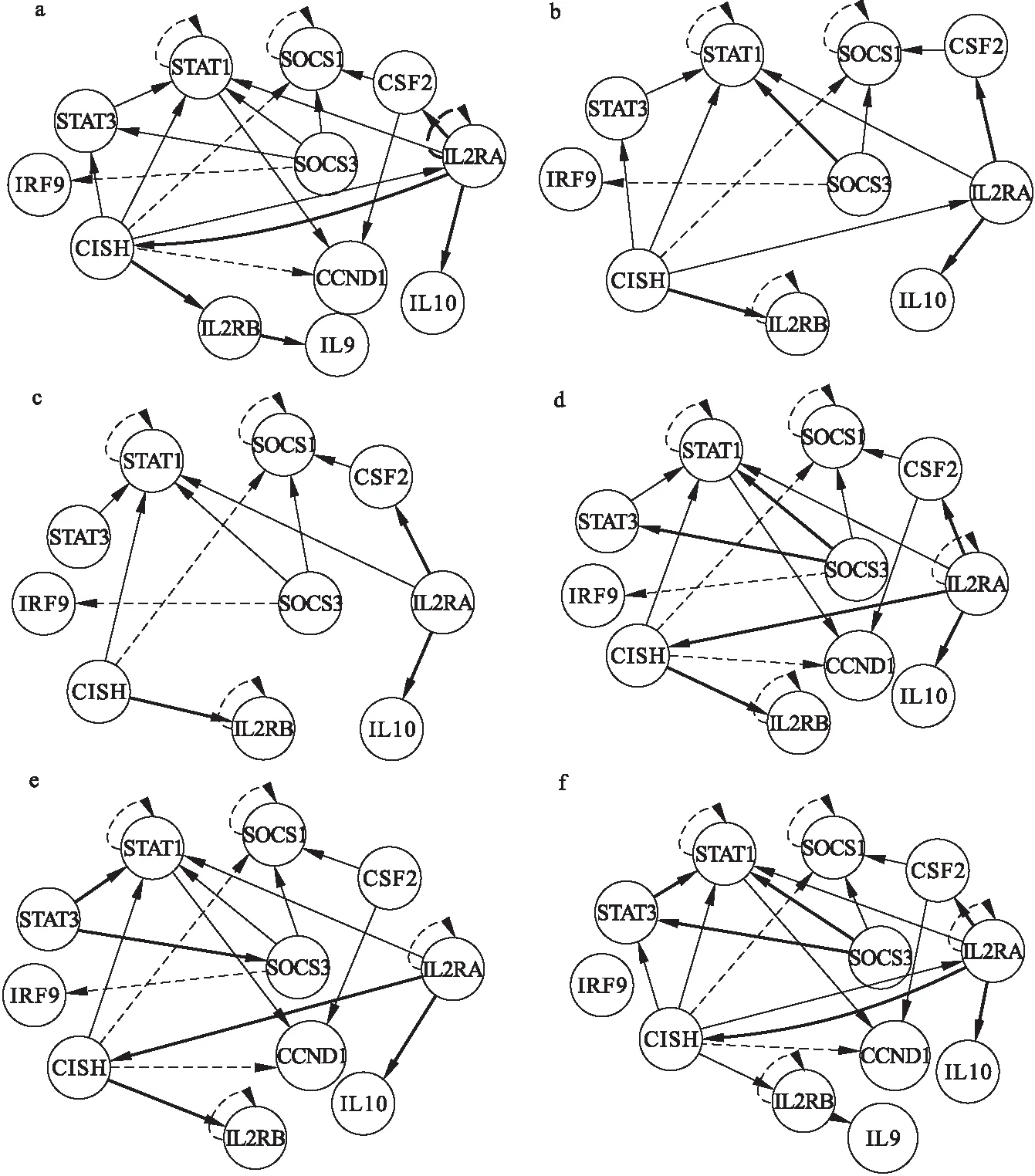
图4 Jak-STAT通路基因ARTIVA 网络结构
2.ARTIVA模型构建网络时受到变量个数的限制,变量多容易出现过拟合现象,同时存在计算困难的问题,最好在构建网络前对变量进行变量筛选。由于实际中主要关心的是不同组间的差异,因此本文选择的是不同组间的差异变量。对于动态数据的变量筛选,可以使用MasigPro、TTCA和edgeR等方法[8]。
3.ARTIVA模型有一个假定,即同一时间点的各变量相互独立,Markov假定使这一条件得到满足。另外,可以看到这一模型可以双向调控和自身调控,从而更好地模拟实际生物过程。
4.ARTIVA模型参数估计,需要假定模型参数的先验分布。选择不同的分布及其参数,网络构建结果不同,需要根据实际问题选择。原作者推荐使用伽马分布γ(α=1,β=0.5)。
5.STRING数据库中呈现的是基因/蛋白间的互作关系,如同源或共表达,ARTIVA网络构建方法是对分子间的调控关系/因果关系进行推断。互作关系与调控关系有密切联系但互作关系不等同于因果关联,因此STRING数据库中无法验证到的调控关系可作为进一步实验研究的提示。
