深基坑变形计算及预测模型探讨
2018-11-03李慎锋刘立伟张吉庆邵海波侯中伟
李慎锋 刘立伟 张吉庆 邵海波 侯中伟
(青岛瑞源工程集团有限公司,山东青岛266555)
0 引言
随着地下空间的开发,基坑深度也越来越大。深基坑的开挖必然会引起土体应力场的变化,这就增大了施工难度,增高了危险系数。因此,预测深基坑变形趋势就意义非凡。国内学者夏明耀[1]进行了基底位移的相似模拟试验,得出相应的经验公式;学渊[2]基于非线性Biot理论提出一种估算深基坑侧边变形的方法;国外学者Ng[3]研究了不同类型深基坑围护结构和基坑周围地表沉降的变形特点以及变形趋势;Kung[4]提出了适用范围较广、精度较高的预测基坑变形的半经验模型。本文论述比较了几种深基坑变形计算经验方法和预测模型,最后认为灰色理论模型,可用于把握深基坑的施工质量和安全。
1 深基坑变形计算方法
1.1 地下连续墙水平位移经验法
国内外许多学者通过总结工程实测数据和有限元计算等方法,发现深基坑围护结构变形与基坑开挖深度存在比例关系,具体关系与土质和支护方式有关[5]。
1.2 地表沉降计算
地表沉降有两种典型的形式:三角型沉降和凹槽型沉降。在进行悬臂开挖或当围护结构发生大变形时,地表产生三角型沉降,且最大沉降值在墙体边缘处;当地基刚性比较大或墙底入土深度较大时会产生凹槽型沉降,最大沉降位置在距离墙体一定距离处,见图1。
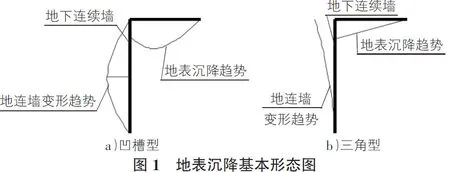
Peck[6]基于大量的实测数据绘制了预估地表沉降的经验曲线,用来反映地表沉降可以结合现场土质条件和施工方法来估算。具体表达式为:
δ=10×K×a×H
(1)
其中,K为修正系数,对于地连墙取0.3,柱列式围护结构取0.7,板桩及排桩取1.0;H为开挖深度;a为土体沉降与开挖深度比值。
1.3 坑底回弹量计算
目前有许多计算基坑底部回弹量的方法和公式,且不同公式不同方法得到的结果也是各不相同。本文用于计算的经验公式都来自于相似模拟试验结果。
1)同济大学进行基坑回弹的试验后提出基底回弹量δ的经验公式如下式:
(2)
(3)
2)坑底隆起主要是塑性变形,采用土工离心模型试验法得到:
δ=0.5H+0.04H2
(4)
3)宰金珉提出了一种简化方法:
(5)
其中,m为单位开挖厚度的质量;H为开挖深度,m=Vγ/H。
2 深基坑变形预测模型概述
2.1 灰色系统理论
灰色系统理论,是一种研究样本数据较贫乏的不确定性问题的方法。其实施步骤有生成、建模、预测等构成。具体步骤如下。
2.1.1 灰色生成
使用灰色系统理论分析得基本要求是样本数据数目不小于4。运用“生成”原理,可以让初始数据具有更强的规律性。按性质分,有:累加生成型、累减生成型、均值生成型、极比生成型[7]。
1)累加型生成。
令T(0)={T(0)(1),T(0)(2),T(0)(3),…,T(0)(n)}为初始数列,生成数列记为T(1)。
T(1)={T(1)(1),T(1)(2),T(1)(3),…,T(1)(n)}
(6)

2)累减型生成。
此过程亦可理解为累加的逆运算,记为IAGO。如果令T(n)表示n次生成数列,则i-IAGO表示对T(n)作i次累减。以i=1为例:
α(1)(α(n)(k))=α(0)(T(n)(k)-α(0)(α(n)(k-1)))
(7)
3)均值型生成。
4)极比型生成。
极比生成是极比σ(k)和光滑比ρ(k)的合称。令{T(0)}为初始数列,T(0)={T(0)(1),T0(2),T(0)(3),…,T(0)(n)},则σ(k)是T(0)的级比:
(8)
T(0)的光滑比可表示为:
(9)
2.1.2灰色GM(1.1)模型
灰色GM(1.1)模型其数学形式是只含一个变量的一阶微分方程式,具体建模步骤如下所述:
1)设初始数列{T(0)},通过前述任一种灰色生成方式得到生成数列,此处以累加生成为例,则得到1-AGO生成数列;

2.1.3残差GM(1.1)模型
残差GM(1.1)模型建模过程与2.1.2相似,只是当系数处于某个范围中时需要对模型进行残差修正。
2.2 灰色马尔科夫链预测模型
灰色马尔科夫预测模型的理论基础是灰色马尔科夫链模型,具体的建模步骤如下:
1)建立GM(1.1)模型,计算τ′(k)=S′(0)(k+1)的曲线;
2)结合实际情况考核τ′(k),把初始数据并入状态区间,将考核后的τ′(k)作为标准,按需求做出τ′(k)的平行曲线,划分出状态区间;
3)计算转移概率:由状态Qi经m步转移到Qi+m的概率P可以通过落入状态区间的样本数与初始数据的比值得到;
4)确定未来状态;
5)确定预测值;
6)计算残差(精度检验)。
2.3 BP神经网络模型
BP神经网络是由输入层、隐含层、输出层构成的多层网络,层与层之间相互独立。一个M层、N单元的神经网络,单元之间无跳跃接受关系,符合Sigmoid函数特征,设初始S个样本,任取一个样本k,其输入向量记xk(n维),输出向量记为dk(m维)。下面以第一层第k个单元为例,第l个样本输入后,可以将节点k的输出值表示为下式:
(10)

当反向传播时,目标函数是期望值dk和实际输入值yk的误差的平方和,即:
(11)
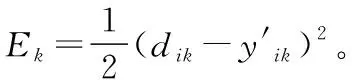
(12)
经过上述转变后,神经网络的学习过程与最优化问题类似。
2.4 灰色马尔科夫—BP神经网络组合模型
这两种模型的组合,使预测模型既避免了指数函数的线性问题,还具备通过学习提高精度的优点。具体建模过程如下:
1)由初始数据建立GM(1.1)模型,得到初步预测结果;
2)用1)所得结果构造BP神经网络的输入序列;
3)对网络进行学习训练。
2.5 预测模型综述
1)灰色系统模型对原始数据依赖较少,适合样本数较少的短期预测,用于中长期预测则随机性过高,精度较低。
2)灰色马尔科夫链预测模型本质上仍是灰色系统模型,只是在预测值的处理上更优越。
3)BP神经网络模型具有较高的精度,但要基于大量的样本数据,而且迭代算法收敛慢,耗时较多。
4)灰色马尔科夫—BP神经网络组合模型结合了前三个模型的优点,但是也有不少缺点,如建模过程比较复杂,建模时需要综合考虑较多的因素,还有就是样本数据先经马尔科夫链预测,再导入神经网络训练时会产生误差,而且这个误差难以控制。
综上所述发现,灰色GM(1.1)模型虽然精度较低,但是其在基坑开挖这样的短期工程实际问题中更具有操作性,得到的上限控制值精度可以满足工程要求,能够对基坑开挖过程中变形控制提供足够的参考依据。
