下支撑机构锁紧装置可靠性仿真与分析

提亚峰，季宝锋，杨 柳，闫 冰，张建国

（1. 北京宇航系统工程研究所，北京，100076；2. 北京航空航天大学，北京，100191）

0 引 言

逃逸系统主要包括逃逸塔、整流罩以及逃逸固体发动机等，专门负责故障情况下的低、中、高空航天员的逃逸救生[1,2]。下支撑机构位于逃逸整流罩内，是载人飞船和头部整流罩间逃逸时的主传力结构，其能否正常工作直接影响逃逸救生，是保证飞船安全逃逸的关键机构之一。火箭正常飞行时下支撑机构依靠弹簧紧压在飞船的支承面上，起到弹性支撑作用，在飞行中保证下支撑机构各支承面随船体一起移动；逃逸飞行时通过火工装置的作用，下支撑机构前后锁紧接头被锁定，对飞船的支撑由弹性变为刚性，下支撑机构承受逃逸飞行时飞船传递给头部整流罩的轴向、横向载荷，从而使飞船在逃逸发动机推力作用下逃离故障火箭。

作为下支撑机构核心功能部件的锁紧装置，是使下支撑机构对飞船的支撑由弹性变为刚性的关键装置，其工作可靠性直接关系到逃逸飞行的成败，因此锁紧装置应具有高承载、高可靠性。由于锁紧装置的锁紧力影响因素十分复杂，历次锁紧试验中锁紧装置的锁紧力离散性较大。为确保载人飞行试验的成功，满足可靠性指标要求，应提高锁紧装置的可靠性。

1 下支撑机构锁紧装置结构

下支撑机构安装在载人飞船整流罩的后锥段内，间隔120°分布，用于承载逃逸飞行时飞船向整流罩传递的巨大惯性载荷，下支撑机构的前、后分别安装一个锁紧装置。

由于锁紧装置结构复杂，影响锁紧性能的因素很多，可靠性指标要求不低于 0.9999，完全通过试验研究影响因素来提高可靠性需要进行的试验将多达256套次，试验规模大、周期长、费用高。为合理高效地提高锁紧装置的可靠性，确定了以可靠性仿真分析为主、试验为辅的研制方案，通过对锁紧装置进行可靠性仿真分析，从诸多影响因素中确定主要影响因素，然后针对主要影响因素设计可靠性验证，从而确定合理有效的结构方案。

2 下支撑机构锁紧装置可靠性分析基础

机构可靠性设计，就是要充分考虑机构的工作环境对机构的影响，实现机构的功能和性能，满足可靠性特征量的要求[3]。为全面地对下支撑机构锁紧装置进行可靠性分析，按机构可靠性设计要求，对锁紧装置进行定性和定量可靠性分析。定性分析进行锁紧装置的系统功能分析和故障分析，定量分析通过相关分析软件进行可靠性分析。

2.1 锁紧装置系统功能分析

根据锁紧装置的结构和功能，可将锁紧装置分为控制组件、锁紧组件、支撑组件。控制组件功能为推压弹性组件，为锁紧装置提供正压力；锁紧组件功能是提供锁紧摩擦力；支撑组件功能是安装各零部件，保持其装配位置关系。

2.2 锁紧装置故障分析

在功能分析的基础上，进行锁紧装置故障判据的确定。在正常的设计、使用、维护和环境条件下，凡是满足不了锁紧装置功能及设计指标要求的事件，均定为系统故障。寿命期内锁紧装置自身引起的故障均定为影响锁紧装置基本可靠性的关联故障[4]；在任务剖面中凡不能完成锁紧装置正常功能的故障均定为影响任务的关联故障[3]。

锁紧装置具体故障判据如下：

a）零件级产品故障判据。承载件因不满足强度、刚度要求而发生强度破坏；传力件表面硬度不满足要求而发生的压溃；零件由于加工残余应力引起的过大变形；零件表面清洗不干净或工艺不稳定引起的表面附着颗粒物或平面度超差。

b）组件级产品故障判据。弹性组件提供压紧力不足；装配组件因装配过程中环境冲击或零件公差引起的组件配合超差等；运动组件发生因零件变形或配合变形等。

3 锁紧装置可靠性仿真分析

通过功能分析和故障分析并结合摩擦学理论可知，对性能有影响的主要因素影响了装置内摩擦装置间的犁沟效应。因此可确定对锁紧装置进行可靠性仿真的主要内容是研究摩擦装置间的犁沟效应对锁紧装置的预位移的影响。

下支撑机构锁紧装置可靠性分析的思路是：在锁紧装置功能分析和故障分析的基础上，考虑摩擦间接触面犁沟效应[5]，对锁紧装置进行摩擦学理论建模，通过有限元软件及机构系统可靠性分析软件ARAMS进行可靠性分析。首先通过有限元仿真来验证摩擦学公式建立的锁紧装置模型；然后通过动力学仿真给出锁紧装置预位移与摩擦力间的关系；最后通过摩擦学理论，建立基于犁沟效应的功能函数，利用可靠性分析优化软件进行功能函数的可靠度分析计算。

3.1 通过有限元软件对锁紧装置性能分析

利用通用显式动力学分析软件 LS-DYNA建立锁紧装置的有限元模型，对锁紧装置锁紧后的内外摩擦结构间接触状态下的特性进行研究以达到如下目的：a）仿真分析锁紧装置锁紧状态下单摩擦副的剪切应力大小；b）在锁紧装置锁紧时，假设各摩擦副产生的剪切应力大小一致，计算锁紧装置由于粘着效应[6,7]所产生的摩擦力。

通过对单摩擦副模型、多摩擦副模型及考虑温度影响的多摩擦副模型的仿真分析结果都证明在犁沟模型中，剪应力表征粘着摩擦力的情况；单摩擦副和多摩擦副计算出的组件摩擦副锁紧装置锁紧力基本相同，说明每个摩擦副产生的摩擦力大小基本相同。由于摩擦结构存在氧化，摩擦系数、屈服极限等都有一定程度的离散，因此计算摩擦力与锁紧装置实际工作过程中提供的锁紧力会稍有不同。

通过对锁紧装置不同加载方式的仿真结果对比，说明锁紧装置在未给定压紧力时，不宜承受冲击载荷，要求在工作过程中压紧力的压紧与载荷的冲击要有严格的时序关系。

通过对锁紧装置不同环境温度下的仿真结果，说明环境温度变化对于锁紧装置锁紧能力有一定的影响；在低温环境中，由于材料的塑性流动能力减弱，结构间的摩擦系数增大，导致剪切应力增大。具体计算结果如图1～7所示。

图1 单摩擦副剪切应力计算云图Fig.1 Single Friction-shear Stress Simulating Results

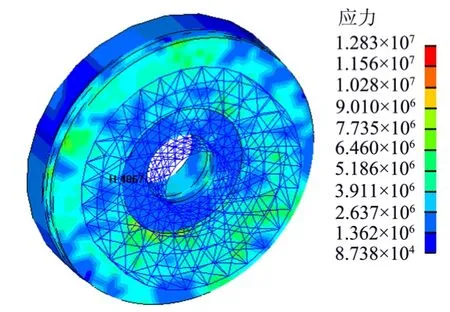
图2 渐变载荷下多摩擦副剪切应力云图Fig.2 Multiple Vice-shear Stress under Gradational Loading

图3 渐变载荷下结构位移曲线Fig.3 Structural Displacement Curve under Gradational Loading

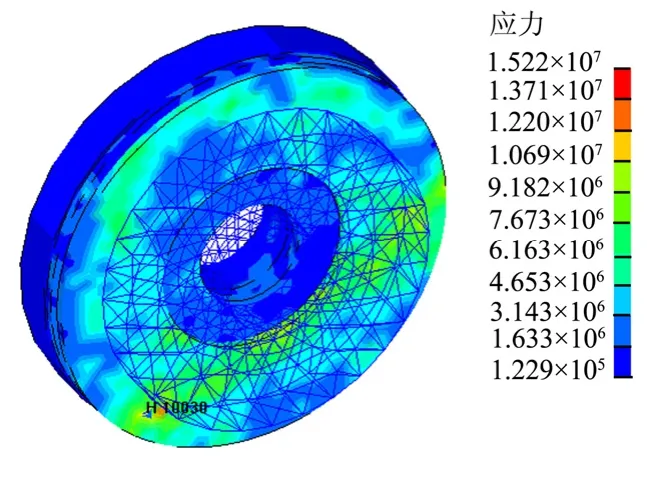
图4 多摩擦副冲击载荷下剪切应力计算云图Fig.4 Shear Stress under Multiple Friction Vice-ballistic Loading

图5 冲击载荷下结构位移随时间变化曲线Fig.5 Structural Displacement Curve under Ballistic Loading

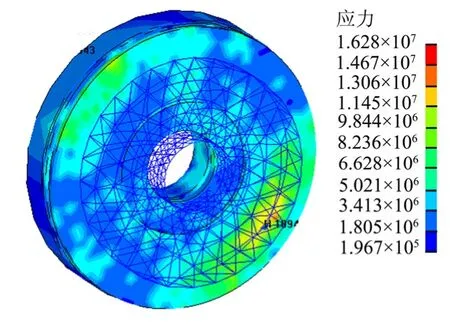
图6 -50℃环境温度下多摩擦副剪切应力云图Fig.6 Multiple Friction Vice-shear Stress under -50℃Environmental Temperature

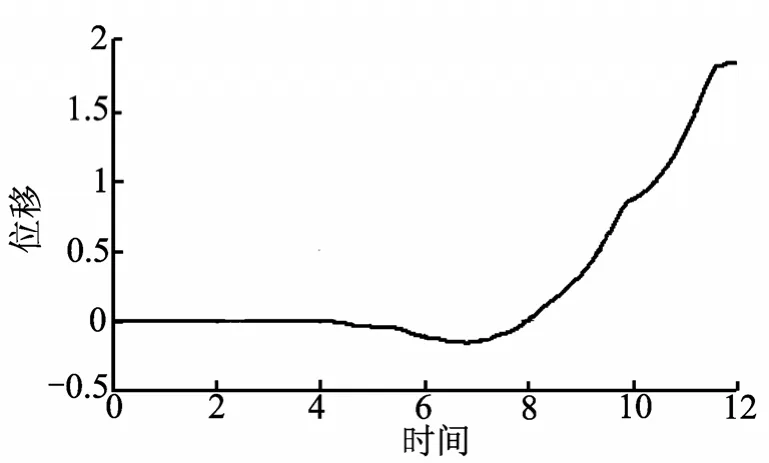
图7 -50℃环境温度下结构位移曲线Fig.7 Sructural Displacement Curve under -50℃ Environmental Temperature

3.2 通过动力学软件对锁紧装置性能分析

利用动力学仿真软件 ADAMS，建立锁紧装置的机构模型，对锁紧后的摩擦结构运动状态进行动力学仿真分析以达到如下目的：a）仿真分析锁紧装置锁紧过程的动力学响应；b）给出锁紧装置中各重要零部件的运动参数和受力情况及其相应的变化情况。仿真结果如图8～14所示。

通过对单组摩擦结构和多组摩擦结构的机构运动模型动力学仿真分析，得出如下结论：

a）通过对各个摩擦结构的受力和预位移进行对比分析发现，越靠近法兰盘，摩擦结构受力越严酷，预位移越大；

b）通过和单组摩擦结构仿真模型的对比分析，得到多组摩擦结构与单组摩擦结构模型的仿真情况基本相同，与有限元分析的多摩擦副和单摩擦副结论一致。

图8 锁紧装置单组摩擦结构ADAMS动力学模型Fig.8 ADAMS Dynamic Model of Single Frictional Structure in Locking Apparatus

图9 摩擦结构所受正压力、负载和预位移输出曲线Fig.9 Positive Stress, Negative Stress and Pre-displacement Curve by Frictional Structure

图10 紧贴压盘的摩擦结构受力和位移输出曲线Fig.10 Stress and Displacement Curve of Frictional Structure Assembled Tightly to Panel

图11 摩擦结构的预位移输出曲线Fig.11 Pre-displacement Curve of Frictional Structure

图12 单组摩擦结构模型中载荷-预位移曲线Fig.12 Stress vs. Pre-displacement in Single Frictional Structure Model

图13 摩擦组件结构中紧靠压盘的摩擦结构的载荷-预位移曲线Fig.13 Stress vs. Pre-displacement of Frictional Structure Assembled Tightly to the Panel in Frictional Component Structure

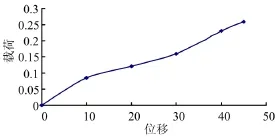
图14 摩擦组件模型中紧靠压盘的摩擦结构的载荷-预位移曲线Fig.14 Stress vs. Pre-displacement of Frictional Structure Assembled Tightly to the Panel in Frictional Component Model

3.3 通过分析优化软件对锁紧装置可靠性分析

在已知锁紧装置的工艺尺寸、受力状态、材料属性后，考虑粘着效应和犁沟效应，单摩擦副单峰犁沟效应的模型为

式中bτ为基体（摩擦副中较软的金属）剪切强度；sσ为基体（摩擦副中较软的金属）屈服极限，sb3στ=；h为硬峰嵌入软金属的深度；d为犁沟宽度。

根据摩擦学理论，犁沟效应产生的摩擦力与粘着效应产生摩擦力间的关系为

式中 θ为模型半角，θtan2hd=，其中θ的一般取值范围为30～60°，当θ=45°时，粘着效应与犁沟效应对于摩擦力的影响相同。在下文的分析中，近似地将犁沟模型的犁沟半角考虑为平均情况，即θ=45°。

考虑多峰，即接触峰点为

一般情况下粗糙表面的凸峰高度服从Gauss分布，此时的均方差σ与表面粗糙度aR具有互换性，如下式：

模型的表面粗糙度为1aR=3.2 µm，2aR =3.2 µm，由此可得：

两组摩擦结构之间的接触面积为

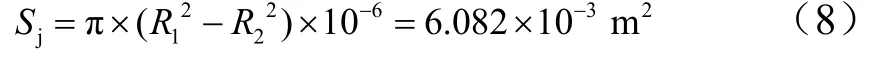
式中1R，2R为两组摩擦结构的直径。

单个犁沟模型所占投影面积：

式中 d为犁沟宽度，根据经验数据选取为2 µm。

两组摩擦结构间峰点数为

锁紧摩擦结构单摩擦副间摩擦力公式模型如下：

由此根据典型的应力-强度干涉模型，建立下支撑机构锁紧力不足的功能函数：

式中bτ为基体I剪切强度；sσ为基体Ⅱ屈服极限；θ为模型半角；R为给定许用载荷；F为响应值。

将功能函数代入可靠性分析优化软件ARES进行显式的功能函数可靠度分析。选择屈服极限、凸峰数目、剪切强度、犁沟深度、犁沟半角以及承受载荷作为随机变量。对各变量的分析结果如图15所示。

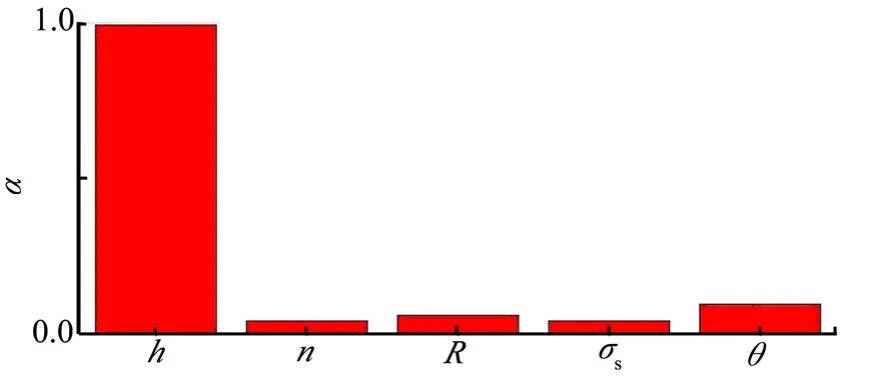
图15 参数重要度结果Fig.15 Parameters Importance Degree Result

通过对各参数的优化分析，得到优化后的各变量的重要性结果，如图16所示。

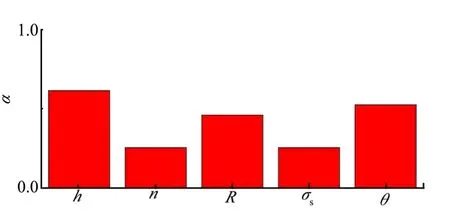
图16 参数重要度优化结果Fig.16 Parameter Importance Optimization Results

4 结 论

通过摩擦学粘着理论和表面形貌理论结合，建立了锁紧装置锁紧力的数学模型，并在此基础上进行锁紧装置的可靠性分析。主要结论如下：

a）通过锁紧装置的有限元模型验证公式中的粘着项，证明了公式建模中参数选择的正确性。摩擦组件各副产生摩擦力大小基本相同、锁紧装置未给定压紧力时不宜承受冲击载荷、低温状态下结构间摩擦系数和剪切力都会增大；

b）通过对摩擦组件进行动力学的仿真分析，验证了摩擦组件预位移与摩擦结构承受载荷之间的关系，得到预位移变化的趋势和摩擦力与预位移之间的关系，越靠近法兰盘结构受力越大、预位移越大；

c）在合理验证公式的基础上，利用ARES软件进行可靠度的计算以及参数重要度分析，得到犁沟半角、犁沟深度等影响装置锁紧可靠性的重要参数，并通过优化得到理想的参数结果。