小区电动汽车群柔性充电控制策略
2018-11-01张锐明
黄 亮,朱 阳,张锐明
(1.武汉理工大学 自动化学院,湖北 武汉 430070;2.广东泰罗斯汽车动力系统有限公司,广东 佛山 528000)
现代化社会的迅猛发展与人民生活水平的日益提高,使得电动汽车行业不断蓬勃发展。文献[1]以电网环境为研究对象,利用削峰填谷的策略处理大规模电动汽车负荷对电网的冲击。文献[2]提出了一种改进有序充电的梯形充电方法,缓解了有序充电中电荷冲击的问题。文献[3]对限定配电网容量下的有序充电方法进行改进,通过网格选取的办法进行充电方法的选取,然后利用遗传算法的优化求解实现了充电控制算法优化。传统的柔性充电技术目标主要在功率分配方法和充电电池的保护方面,其缺陷在于各自的优化目标单一,且主要针对充电站与充电设施的充电过程而没有考虑配合电网侧以及用户群充电需求等。
笔者以居民小区的电动汽车群与充电站为模型实现小区内的柔性充电策略,具体优化目标为:①如何在小区内正常的负荷下满足电动汽车群的充电需求,且不超过配电容量;②利用电网的峰谷分时电价提高充电效益,实现削峰填谷;③在充电站负荷曲线的基础上完成充电站内充电模块的能量分配,实现柔性充电。笔者按照分步求解的方法实现3个目标的优化:第一步,采用约束条件实现对于目标①的选择;第二步,以峰谷电价为最优化选择目标,采用遗传算法求解实现目标②的优化;第三步,由前两步可得出充电站的负荷情况,将此负荷以数学网格分析对充电站中的充电模块进行功率分配,实现柔性充电。
1 小区充电模型分析
1.1 车辆返回时间
车辆返回时间是决定车辆起始充电时间的关键因素。假设车辆每天最后一次返回家中即进行充电,根据美国交通部调查(national household travel survey,NHTS)报告数据可得每天私家车最后一次返回时间的概率分布,近似于正态分布,如图1所示。

图1 车辆返回时间分布
私家车习惯回家时间统计的正态分布概率密度函数可近似表示为[4]:
(1)
0≤x≤24,μc=18.67,δc=0.741
1.2 车辆充电电量
由于电动汽车的渗透率低,私家车回家充电的SOC分布状态无法直接统计,笔者按照电动汽车用户充电开始时的SOC调研数据进行近似分析,用户车辆接入充电时电池SOC的调研数据如图2所示。

图2 充电起始SOC分布
电动汽车充电负荷研究采用文献[5]中的概率密度函数,如式(2)所示。
(2)
0≤x≤1,μs=0.576 4,δs=0.147 45
1.3 蒙特卡洛模拟方法
当前的电动汽车发展技术下,找到比较典型可靠的规模性小区比较困难,而对于数据不完备问题,一般采用蒙特卡洛方法进行模拟计算[6]。简单地理解,蒙特卡洛方法是一种在数学上的随机抽样采集处理方法,利用该方法的关键是弄清研究问题的所有模型影响因素,通过综合研究所有影响因素的概率分布函数,求解出相应的概率分布函数。然后在高级计算机上采取大规模抽样统计,模拟的数据量越多,该模拟方法得出的结果的准确度越高。如某模型Z={Y1,Y2,…,YN}由N个不同的已知概率模型组成,可以采用该方法抽样得出Z的结果,然后反复模拟得出Z的概率分布特性。
1.4 小区居民用电信息
小区中的主要电荷信息限制为小区配电变压器的额定容量,基础负荷曲线为居民正常的电量用度,通过记录整时刻的某小区电表负荷信息,得到该居民小区负荷曲线,如图3所示。

图3 居民小区负荷曲线
另外,小区的充电策略选择需要考虑分时电价信息,该小区不同时刻的电价信息如表1所示。
2 充电控制策略
2.1 充电控制流程
柔性充电的选择流程主要分3步完成:①统

表1 某小区分时电价信息
计充电桩上传的电动汽车BMS信息;②依照电动汽车充电时序信息,综合各个时段电价信息求解充电方案;③按照一定的选择方法寻求最佳的充电方案,其主要控制流程图如图4所示。

图4 充电站充电流程图
2.2 目标函数与约束条件
笔者主要考虑用户层和电网层的多目标函数进行优化求解。
(1)用户层目标。电动汽车用户的优化目标是在满足电动汽车用户充电需求的前提下进行的,可作为约束条件。因此电动汽车用户侧的优化目标为所有用户充电费用最少,如式(3)所示。
f1=min∑[Cfdf+Cgdg+Cpdp]
(3)
式中:Cf、Cg、Cp分别为波峰、波谷、波平时的电网分时电价;df、dg、dp为波峰、波谷、波平时的充电电量;f1为充电站电费总成本。
(2)电网层目标。电网层的优化目标为削峰填谷,解决无序充电中峰上加峰的情况,调度充电负荷。笔者将小区内部的峰谷值作为研究的目标,如式(4)所示。
f2=min(Pf-Pg)
(4)
式中:Pf、Pg分别为小区功率曲线上的峰值和谷值。
由于多目标中各个函数的量纲不同,不可以直接相加,所以需要对上述两个目标进行归一化处理[7],具体方法如式(5)和式(6)所示。
(5)
(6)
式中:Pmax、Pmin分别表示配电网常规负荷的最大值和最小值;d为一天总的充电电量。
运用加权处理后的归一化有序控制充电目标函数为:
minf=a×J1+b×J2
(7)
a+b=1,a≥0,b≥0
其中,a、b分别为两个目标的权重系数。约束条件主要是充电站变压器运行不过载,最大限度地满足充电站用户的充电需求。充电功率约束如式(8)和式(9)所示。
(8)
P(t)≤P0-Pi(t)
(9)
式中:P(t)表示在t时刻所有电动汽车的充电功率之和;P0表示配电网为小区提供的配电功率上限;Pi(t)表示小区用户的正常用电情况t时刻的功率;i表示充电汽车编号;N为充电汽车总数量。用户需求约束如式(10)和式(11)所示。
(SOCA-SOCL)Bi=PiTc
(10)
Tc≤Te-TL
(11)
式中:SOCA为满足充满电动汽车的目标电量;SOCL为电动汽车的初始电量;Bi为电池容量;Tc为充电总时间;TL为电动汽车到达时刻;Te为充电离开时刻。用户需求约束即是满足充满电动汽车的目标电量,在用户离开前,需完成目标的充电任务,若离开时间不足以完成充电任务,则报错不加入调度系统,直接充电特殊处理。
2.3 遗传算法求解
为了更科学地求解优化目标,笔者采取遗传算法[8-9]求解该问题。首先将充电工作日的一天按照15min离散化为96个时段。将充电控制方法的可行解表述为t= {t1,t2,…,t96},其中tj∈{0,1}。tj=0表示电动汽车在第j时段不安排充电,tj=1表示电动汽车在第j时段安排充电。以上述目标函数f作为需求解的算子,通过遗传算法求解得出更合理的答案。电动汽车有序充电策略的具体工作流程如图5所示。

图5 遗传算法改进有序充电流程图
采用遗传算法对电动汽车用户的充电时间进行优化计算的求解步骤如下:
(1)初始化种群。首先随机生成单台的n个原始母体(ts,tend),ts,tend分别表示用户充电时段在接入充电桩的时间和计划离开的时间之间。
(2)基因编码。将(ts,tend)转化为(0,0,0,…,1,1,1,…,1,0,0,…,0)来表示车辆的充电安排。
(3)选择因子。对上述函数求倒数计算并作为选择因子,使得用户花钱少且削峰填谷的优秀基因能够保留下来用作遗传:
fi=1/fi(ts,tend)
(12)
(4)基因选择。通过上述算子选取,求出各个物种的选择概率,选择i个体的概率为:
(13)
(5)变异处理。设置变异概率Pm=0.015。由于变异处理需要保证整体的充电时间不变,即0,1数目不变。变异优化[10]过程如图6所示。

图6 变异操作改进示意图
(6)多代遗传求解。设置一定的交叉遗传代数,经过多代的配对变异达到输出条件,得出最优的结果。
3 功率分配策略
3.1 柔性充电需求
充电站的目标充电负荷曲线代表一天内的所有总的电动汽车充电任务,如图7所示。根据柔性充电的要求[11],功率分配的目标要求有两点:①保证充电模块的负载率在0.4~0.7之间,此时充电模块具有最高的充电效益,并有利于延长每个充电模块的使用寿命;②在功率共享的条件下实现各个冗余模块的休眠与轮休,保证每个功率模块的能量支持负担上的平衡,有利于充电站的长期稳定工作。

图7 有序充电的等效面积图
令充电总负荷面积为E,充电模块数量为N,为实现柔性充电目标,则一天之内理想的调控目标为每一个充电模块的充电负荷平均分配,即每一个充电模块每日的负载为E/N。假定每一块充电模块的充电功率为P,由柔性充电调控研究可知,充电模块工作负载在0.4~0.7之间能够保证最高充电效益,取该系数为η。因此,每一个充电模块的实际充电功率为η×P,那么每一个充电模块的工作时间为E/(η×P)。
3.2 功率分配方法
笔者拟采取一种近似计算的方案进行该问题的求解,首先将1天同样分为96个15 min的工作时段,分别记为T1,T2,…,T96,由上述的充电站有序充电负荷图可以得出,在一天之内的96个时段,各个时段充电站的总电能的计算方法为:
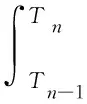
(14)
由此积分方法可以求出96个时段中各个时间段的平均功率,如式(5)所示,其中t表示时间长度,文中取t=15 min。
(15)
由充电站中可控能量模块堆的数量和每一个能量模块功率,可以求出每一个可调控分配的能量矩阵堆的功率P0,继而可以求出每个时间段内至少需投入的能量模块堆数量Zn:
(16)
由上述计算方法可以得出1天96个时段内的工作能量模块堆数组Zn=(Z1,Z2,…,Z96),假设充电站内能量模块堆的总数量为m,理论上讲,每个能量模块堆可以参入的时段为一天96个时段,也可以完全不参入。为了实现柔性充电功率平均分配的要求,则每个模块参入的时段数目y应相等,以满足每个能量模块堆的整体时长与负担相等,即:
为正整数
(17)
此时该方程有两种情况,一是y有正整数解,二是y没有正整数解,笔者对于两种情况分别作出以下分类讨论:
(1)y有正整数解。对于每一个能量模块堆可以针对一天的分布时段进行编码(1,0,1,1,…,1,0),其中1,0总数为96,1的数量为y,1表示有能量模块堆参入的时段,0表示没有。则m个能量模块堆存在的编码方案数量N1为:
(18)
在所有的编码方案数目中,根据选择条件(即上述的工作能量模块堆数组)可以选择出符合实际负荷曲线的能量模块堆分布编码方案组(肯定不止唯一解),选择其中的一种作为小区的能量分配方案即可。
(2)y没有正整数解。这说明一日之内的工作负荷无法直接实现功率的平均分配,可以采用一定的解决方法避免此情况,一是调节柔性充电系数η使得y有正整数解,二是采用取余的方法来处理此情况。
(19)
同样地,整除部分m×y依然可以按照情况(1)中的平均分配方法进行求解,关键的问题是余数部分x的分配和处理。x是1到m之间的正整数,首先大部分负荷能量已经在充电站内平均分配,待优化的部分可以如此处理,延长策略的作用周期,1天之内的多余能量是无法平均分配的,而m天的多余能量一定可以在充电站内实现平均分配。能量x在策略作用周期的第1天可以直接分配在1,2,…,x个模块上,能量x在策略作用周期的第2天,可以直接分配在2,3,…,x,x+1个模块上。以此类推,能量x在策略作用周期的第m天,可以直接分配在m,m+1,m+2,…,x+m-1个模块上。那么在一个策略作用周期内,多余能量x同样在一个作用周期内实现了能量平均分配,对于每一个模块的分配时段的求解方法与情况(1)类似:同样采用编码求解,多余的能量x作为随机部分分配在一周某天。以策略中第一天为例,每一个能量模块堆可以针对一天的分布时段进行编码,其中参入余数部分考虑的能量模块1,2,…,x的编码为(1,0,1,1,…,1,0),1,0总数为96,1的数量为y+1,1表示有能量模块堆参入的时段,0表示没有能量模块堆参入的时段。而没有参入余数部分考虑的能量模块的编码与情况(1)中编码一样(1的数量为y)。则m个能量模块堆考虑余数情况下所有的能量模块方案总数N2为:
(20)
每天依照负荷规律去控制能量模块堆的工作时段,实现了充电站内的能量分配。在每一天内各个能量模块堆的功率近似于平均分配(差距在1个时段15 min之内),而在1个策略周期内总的功率实现了平均分配。
4 仿真与分析
4.1 算例参数设置
供电参数的主要限制为当地充电站的变压器限制输出,笔者设置PM=1 000 kW作为电网配置容量,整时小区用电记录见图3。设定充电站电价为1.5元/(kW·h),充电站区域内的成本电价取表1数据计算。以市面上的典型电动汽车为例,取Bi=26.4 kW·h,Pi=6.6 kW,取充电站内的柔性充电车辆为400辆,目标充电SOC值均为95%。
4.2 仿真结果
仿真结果分别如图8和图9所示。无序充电和柔性充电两种模式下充电负荷的分布和充电费用的对比如表2所示。
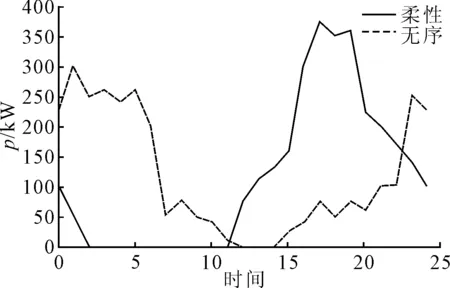
图8 电动汽车柔性和无序充电调度负荷
由仿真结果可得出如下结论:无序充电在负荷曲线上主要分布在10—24 h,而有序充电的负荷分布在0—10 h,在基础负荷的基础上,无序充电会有明显的峰上加峰,而有序充电则出现了填谷效果。从经济角度分析,有序充电利用低谷电价的优势,在一定程度上降低了成本。
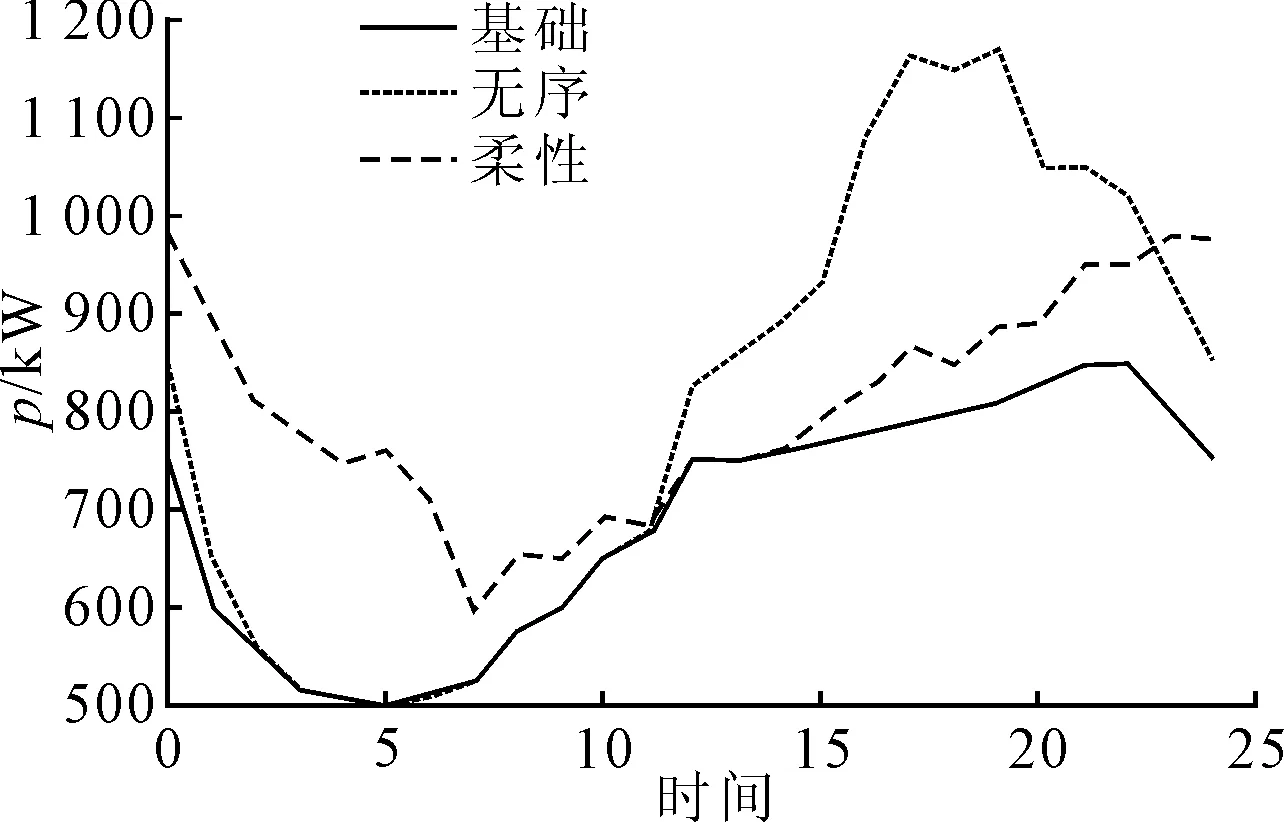
图9 电动汽车区域基础负荷与无序/柔性调度下的区域总负荷

模式峰值/kW谷底/kW差率/%成本/元 无序1 170 50057647柔性98060038158
5 结论
笔者以小区电动汽车用户群为对象进行柔性控制策略研究,提出了一种柔性充电功率分配方法,以分步控制的策略,逐步解决了小区充电中的配电网限制、移峰填谷及充电站内功率分配等问题。经遗传算法优化的有序充电比传统的无序充电有良好的改善效果,极大地降低了负荷峰谷差率、平抑负荷曲线波动;并且进入电价谷段时负荷总量缓步增加,没有产生新的负荷冲击,有利于电网安全平稳运行,也对充电技术发展的柔性充电功率有进一步的研究和探索。
