基于事故预测的高速公路出口匝道类型优选
2018-11-01郭唐仪
夏 雪,郭唐仪,潘 姝
(1. 江苏省连云港公路管理处,连云港 222002; 2. 南京理工大学,南京 210096)
匝道是高速公路与城市道路或其他相交道路的唯一联系纽带,也是高速公路的安全“瓶颈”。事故统计资料表明,出口匝道区域事故率是一般路段的4~6倍,是入口匝道区域事故率的2~3倍[1]。对高速公路出口匝道类型进行优选,有利于改善出口区域行车安全,提升高速公路整体安全水平。
建立高速公路交通事故预测模型,分析事故发生的影响因素和形成原因是交通安全设计、评估及改善的基础[2]。相对于高速公路主线安全的研究,国内外针对高速公路出口安全的研究较为匮乏,尤其是将出口匝道类型作为重要变量的研究方面。Bared等[3]建立Poisson回归模型预测减速车道和匝道主体的事故数;O’Donnell等[4]运用有序Logit/Probit模型研究事故严重程度的影响因素及其级别;马壮林等[5]、李世民等[6]通过构建Logistic模型分析交通事故严重程度的影响因素。
因此,依据美国佛罗里达州交通部的数据,将匝道类型、匝道结构等影响因素作为变量,从事故数及事故严重程度两个方面建立事故预测模型,对出口匝道的类型进行优选,为未来各种类型匝道的规划、设计和建设提供参考依据。
1 出口匝道类型
参考HCM,高速公路分流区影响范围为匝道分流鼻上游500 m至下游300 m。在此范围内,根据高速公路主线与匝道衔接形式及匝道车道数,将出口匝道分为4类,如图1所示。
图1(a)所示为类型Ⅰ:平行式有可选车道的单车道出口匝道。主线上的车道数未减少;出口匝道为单车道;主线与匝道衔接中设有可选车道,行驶在可选车道上的车辆可选择沿主线行驶或驶离主线进入匝道。
图1(b)所示为类型Ⅱ:直接式无可选车道的单车道出口匝道。主线上的车道数减少1条;出口匝道为单车道;车辆直接从最外侧车道驶离主线进入匝道。
图1(c)所示为类型Ⅲ:平行式有可选车道的双车道出口匝道。主线上的车道数减少1条;出口匝道为双车道;主线与匝道衔接中设有可选车道,行驶在可选车道上的车辆可选择沿主线行驶或驶离主线进入匝道,或者直接从最外侧车道驶离主线进入匝道。
图1(d)所示为类型Ⅳ:直接式无可选车道的双车道出口匝道。主线上的车道数减少1条;出口匝道为双车道;车辆直接从最外侧车道驶离主线进入匝道。
其他出口匝道定义为类型Ⅴ。
此外,根据匝道分流鼻至匝道下游末端交叉口的线形特征,将匝道主体结构分为4类,如图2所示。

(a) 平行式有可选车道-单车道出口匝道(类型Ⅰ)

(b) 直接式无可选车道-单车道出口匝道(类型Ⅱ)

(c) 平行式有可选车道-双车道出口匝道(类型Ⅲ)
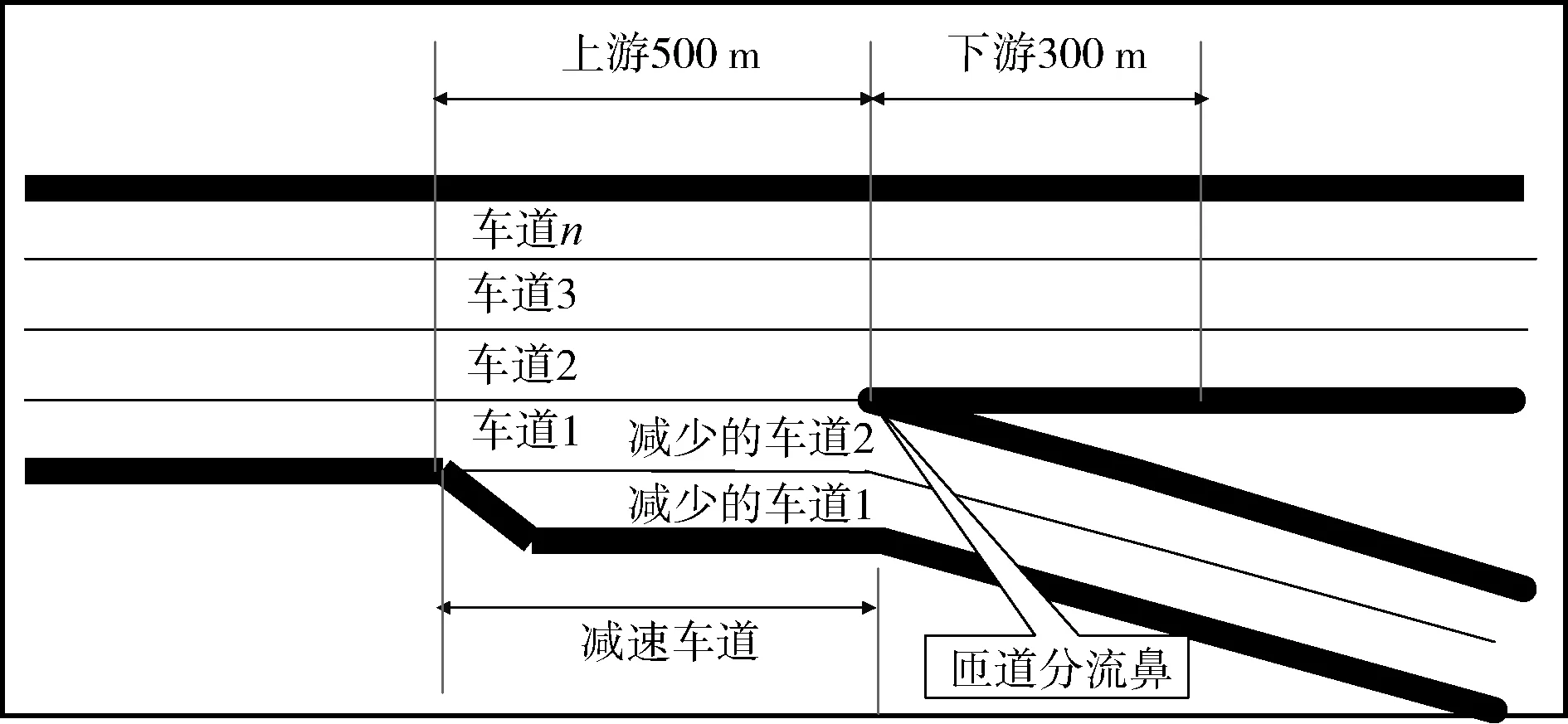
(d) 直接式无可选车道-双车道出口匝道(类型Ⅳ)
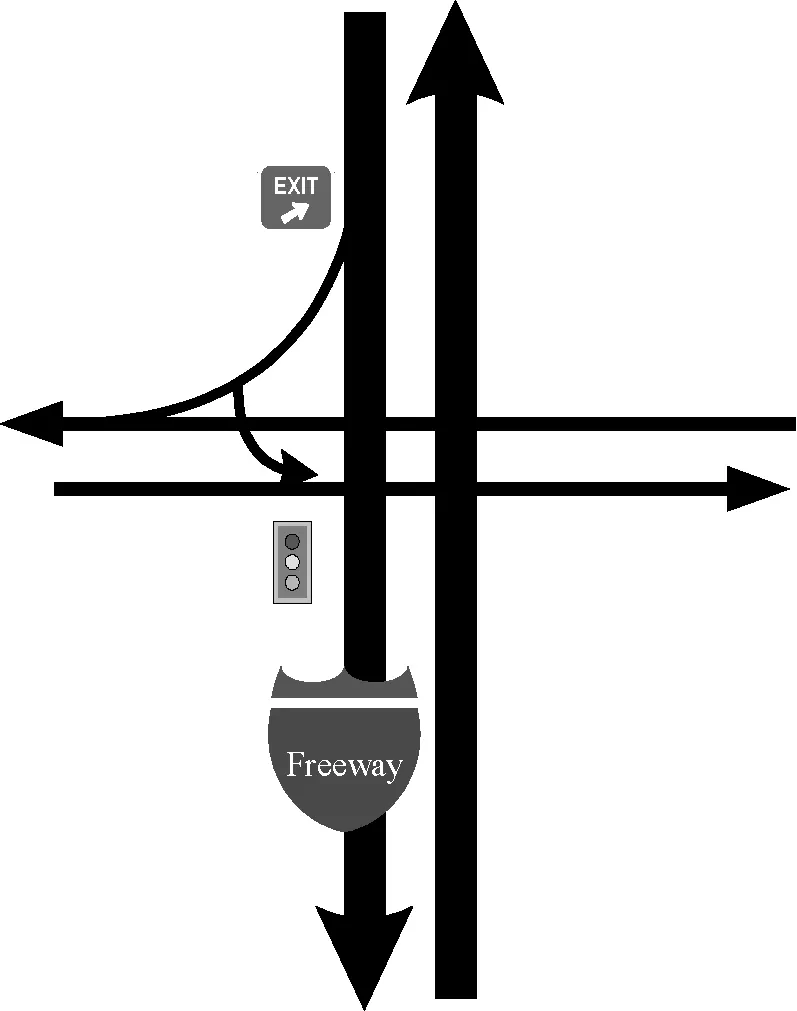
(a) D型(菱形)结构

(b) O型(外连形)结构
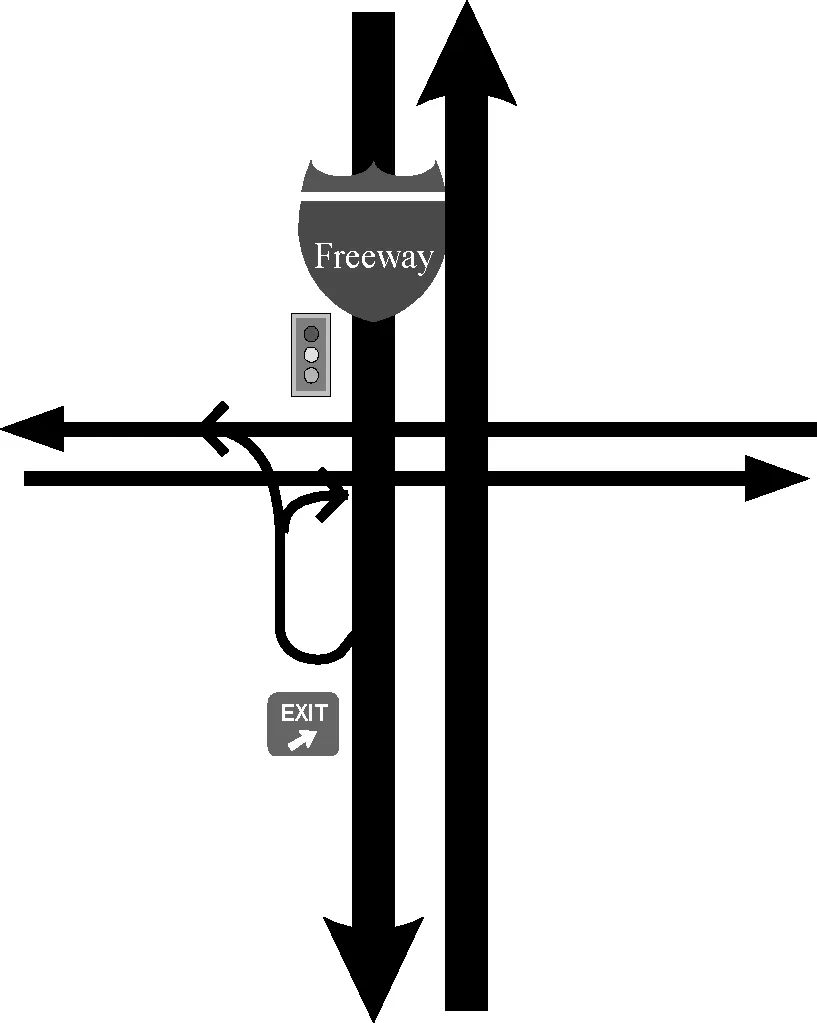
(c) F型(自由流环形)

(d) P型(部分苜蓿叶形)
2 预测模型
2.1 线性回归模型
线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间的关系进行建模的一种回归分析。线性回归模型具有以下的形式:
Y=Xβ+ε
(1)
式中,Y为与交通事故相关的因变量向量,如事故总数或严重事故数等;X为影响因素向量,β表示为对应系数;ε为误差项或者随机变量,与X独立,用于捕捉除X之外任何对Y的影响。
2.2 Logit模型
Logit模型主要用于预测分类事故。如果是根据严重程度分级,因变量是有序的,那么可以根据有序Logit(Ordinal Logit)模型进行预测。
将发生第i类交通事故的影响因素向量记为Xi=(xi1,xi2,…,xin),Xi对第i类交通事故产生的效用记为Ui:
Ui=Vi+εi
(2)
式中,Vi,εi分别表示发生第i类交通事故的效用函数固定项和概率项。Vi一般取Xi的线性形式Vi=βXi=β0+β1xi1+β2xi2+…+βnxin。
当εi服从Logistic分布时,Logit模型如下:
(3)
3 事故预测模型
3.1 数据及变量初选
根据佛罗里达州交通部项目[8],选取了佛罗里达州24条高速公路的405个出口匝道进行研究,其中事故数据是指2004年至2006年,在出口匝道影响区域内的年均事故数。本文从86个可能的影响因素中选取了以下变量作为主要影响因素,如表1所示。
3.2 事故数及事故严重程度的分布检验
在Weibull++7软件中对出口匝道3年的事故数及事故严重程度的非参数分布检验,如表2所示。结果表明:无论是对事故数还是对事故严重程度,对数正态分布和指数分布拟合性都较好。

表1 事故及相关变量统计
注:a:FAI为受伤和死亡事故 (Fatality And Injured),PDO表示仅有财产损失的事故;b:建模方便取对数;c:下游末端连接道路的种类将其分为Highway(1)、Arterial(2)、Freeway(3)以及其他(4);d:末端控制方式:分流型(1)、拓宽型(2)、合流型(3)以及其他(4)。

表2 事故指标的分布检验
3.3 事故预测模型
3.3.1 事故数预测
基于3.1的线性回归模型,事故总数(分流区和匝道段的事故和)模型拟合为:
CrashTotal= -16.162+0.317LnAADTRamp
+3.269LnSDiverge+βType×[Type]
+βConfig.×[Config.]
(4)
式中,βType和βConfig.分别为匝道类型、匝道结构,[Type]和[Config.]为对应的匝道类型、匝道结构,AADTRamp为匝道交通量,SDiverge为分流区速度。模型中各系数来源如表3所示(表中△为参照类,下同)。

表3 参数估计(事故总数模型)
表3模型参数估计表明:
(1) 相对应其他3类匝道的事故数,I型匝道(单车道可选车道的出口)系数最小;而D型结构系数为“+”,其他的为“-”,说明D型结构安全性最差。
(2) 分流区限速对事故数有着最显著的影响。
3.3.2 事故严重程度预测
无事故发生(None)取值为“0”,发生仅财产损失事故(PDO,Property Damage Only)取值为“1”,发生伤亡事故(FAI,Fatality And Injured)取值为“2”。
若将3类事故作为相互间的存在等级关系来对待,有序Logit模型适用性较好。模型中要拟合因变量数-1,即建立两个回归模型,则需要引入联系函数,其广义表达式为:
link[γj(x)]=θj-βTx=θj-(β1x1+β2x2
+…+βmxm)
(5)
式中,γj(x)为第j分类的累积概率;θj为第j分类的常数项;β为未知参数向量;x为协变量。
由于事故严重度分布不均,没有事故发生的频数仅为75次,而发生PDO事故和FAI事故的频数接近,分别为1 816和1 479次。变量值低者发生概率低,事故严重度不服从均一分布和正态分布,也不存在极端值分布。因此,选择负log-log作为联系函数。
以FAI事故为参照,另外两类事故的负log-log联系函数分别为:
Link(Severity=None)
=1.471-(0.078LnAADTRamp+0.512LnSRamp
+βType×[Type]+βConfig.×[Config.])
(6)
Link(Severity=PDO)
=3.354-(0.078LnAADTRamp+0.512LnSRamp
+βType×[Type]+βConfig.×[Config.])
(7)
式中,βType,[Type],βConfig.,[Config.],AADTRamp,SRamp意义同上。模型中各系数来源如表4所示。
基于3.2的有序Logit模型,事故严重度预测模型为:
(8)
(9)
P(FAI)=1-P(None)-P(PDO)
(10)
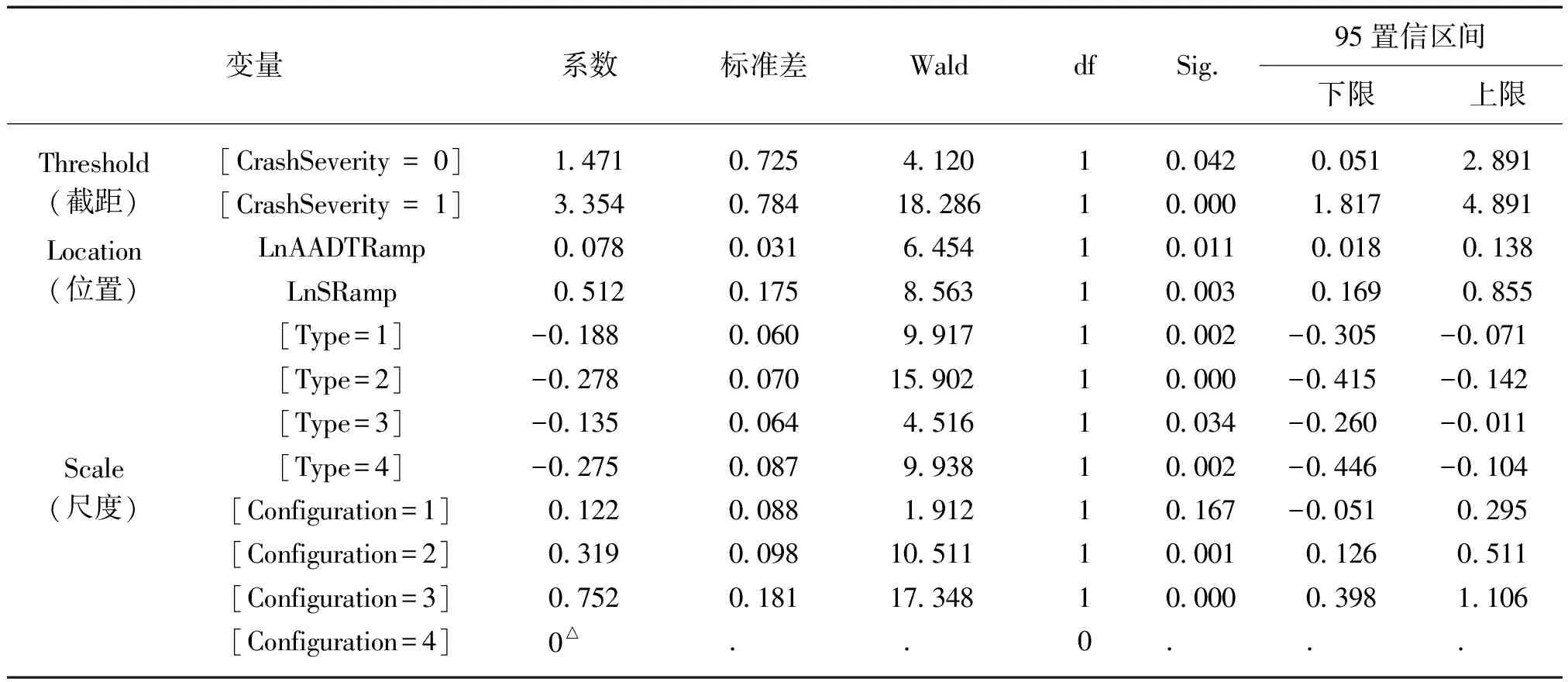
表4 参数估计(事故严重度模型)
4 结论
根据各类型的发生比(exp(B)),以较为安全的类型Ⅰ为基准,将其余3类与之比较,可得不同类型匝道的比选结果,如表5所示。表中数值表示如果在类型Ⅰ匝道上发生一起交通事故或严重伤亡事故,相应在其它类型上发生的事故数。
根据前文分析及表5,类型比选的结论如下:
(1) 总体安全性优劣:类型Ⅰ>类型Ⅲ>类型Ⅳ>类型Ⅱ。

表5 匝道类型评选
(2) 无论是单车道还是双车道,具有可选车道的类型比没有可选车道的安全性能要好,因而类型Ⅰ优于类型Ⅱ,类型Ⅲ优于类型Ⅳ。
(3) 无论是单车道还是双车道,主线车道数没有减少的类型优于有车道减少的,因而类型Ⅰ优于类型Ⅱ,类型Ⅲ优于类型Ⅳ。
(4) 事故严重性方面,分别与类型Ⅰ和类型Ⅲ相比,类型Ⅱ和类型Ⅳ更易发生伤亡事故。
4种不同结构匝道之间的安全性,从历史事故数据来看,各结构之间的事故数和严重性差异不大。从事故数预测模型中可以判断出,P型具有最少的事故总数和FAI事故,其次是O型和F型,D型最差。此结论可为国内出口匝道规划与设计提供一定的参考价值,但需要更多国内出口匝道的实际数据进一步佐证。
