YK3150E数控滚齿机误差补偿技术研究
2018-11-01胡世军
张 龙,胡世军
(兰州理工大学机电工程学院,甘肃 兰州 730050)
我国现代化工业发展进程中,齿轮是不可或缺的机械零件,数控滚齿机床在加工齿轮的过程中起十分重要的作用。目前主要使用误差补偿法来提高齿轮的制造精度,而准确建立机床误差几何模型是进行误差补偿的关键步骤,因此如何建立机床误差几何模型是目前需解决的难题。
近年来,人们大多通过多体系统理论研究法来解决复杂机械系统产生的误差问题。多体系统可以对复杂的机械运动进行概括,能够综合考虑机械系统相邻部件的联系,避免了建模过程中零部件的缺失,该方法具有准确化、公式化、广泛化、便于计算等特点[1]。
本文以多体系统理论研究法为依据,通过对滚齿机床的拓扑结构进行分析计算,得到相邻部件产生的误差,利用坐标变换原理,建立误差几何模型,经过对几何模型进行误差解耦,最终求得机床各轴的误差补偿量。
1 YK3150E数控滚齿机床结构分析
目前齿轮加工的方法主要有两大类,一类是成形法[2],其特点是加工精度和生产效率均比较低,不适合工业大批量生产;另一类是展成法,使用一把刀具,加工相同模数、相同压力角、不同齿数的齿轮,其加工精度与生产效率均比较高,故在工业生产中常使用此方法。齿轮加工的机床类型众多,如滚齿机、插齿机、磨齿机等。本文以滚齿机为研究对象,通过一系列技术手段,提高齿轮的加工精度。
图1为YK3150E数控滚齿机的简化物理结构图,它主要完成3部分运动:
1)主运动,即滚刀的旋转运动。
2)啮合运动,即齿坯和滚刀按照一定的速度比旋转运动。
3)进给运动,即滚刀沿着齿坯轴向进给运动。
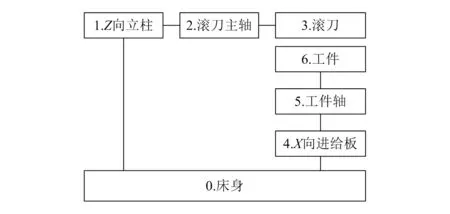
图1 YK3150E数控滚齿机简化物理结构图
2 滚齿机床加工误差几何模型的建立
进行误差补偿最重要的步骤是几何误差建模。当前几何误差建模有诸多方法,例如多体系统理论法[3]、三角几何法、神经网络法和误差矩阵法等,在这些方法中,利用多体系统理论方法来建立误差模型,可以将齿轮机械的复杂性及系统的彼此关系进行综合考量,从而大幅度提高误差模型的精准度,有效克服了误差建模过程的通用性差、自动化程度低等问题。
2.1 多体系统理论及其描述方法
多体系统[4]是对一些复杂机械系统的抽象描述,使用经典力学方法建立微分方程,理论上可以解决任何复杂的机械系统问题,但由于部分系统中内分体数和自由度较多,各个部件间的约束复杂,使得求解所建立的微分方程十分困难,因此使用传统经典力学方法对复杂机械系统进行分析已不能满足现代结构计算的需要。目前普遍利用多体系统理论研究法来解决复杂系统中的问题,该方法主要有两个步骤,第一个步骤是建立模型,第二个步骤是求解模型。在建立模型时,有数学模型和物理模型两种。多体系统理论研究法可以对机械产品中的复杂结构进行简化和抽象,是目前解决复杂机械结构问题的主要研究手段。
2.2 拓扑结构及低序体阵列
应用多体系统理论研究法解决问题的一个重要过程就是得出研究目标的拓扑结构图。假定惯性坐标系是A0,选任意一体作为A1,沿着疏远A1的方向用增进数列来标记各个部件的序号,最后将系统的所有分支全部标记完成。图2所示为YK3150E数控滚齿机的环形拓扑结构图。
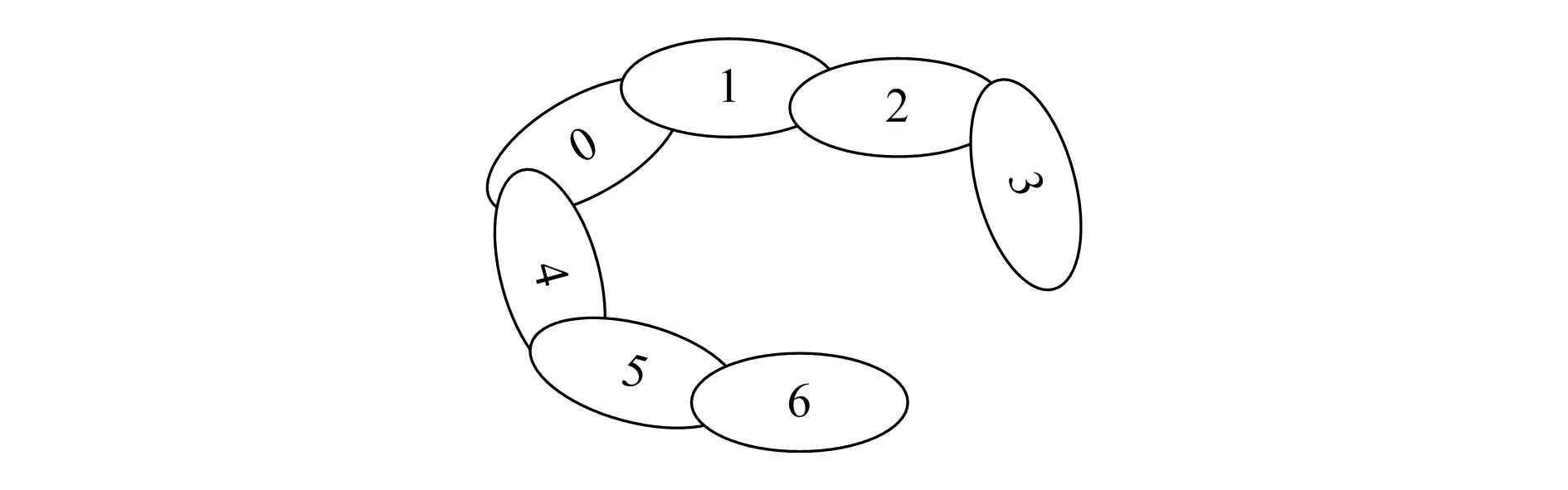
图2 YK3150E数控滚齿机环形拓扑结构图
在多体系统中,一般将构成拓扑结构的单位称作体,常用低序体阵列对其进行数字化表述,如图3所示为YK3150E数控滚齿机低序体阵列表,其中用Lj(k)来描述典型体k的j阶低序体。

123456L0(k)123456L1(k)012045L2(k)001004L3(k)000000
图3 YK3150E数控滚齿机低序体阵列表
2.3 相邻体误差分析
建立数控滚齿机床的几何误差模型,利用矩阵的运算方式,把数控滚齿机各部件的传动误差、安装制造误差、运动误差统一叠加在刀具和工件对应的位置矢量误差上,并建立误差特征矩阵。研究各个相邻体的特征矩阵,通过拓扑结构把这些特征矩阵相乘,进而得到刀具和工件的最终误差矩阵Tmn。
Tmn=Tmn,pTmn,peTmn,sTmn,se
(1)
式中:Tmn,p为邻体的位置矩阵;Tmn,pe为位置误差矩阵;Tmn,s为位移矩阵;Tmn,se为位移误差矩阵。
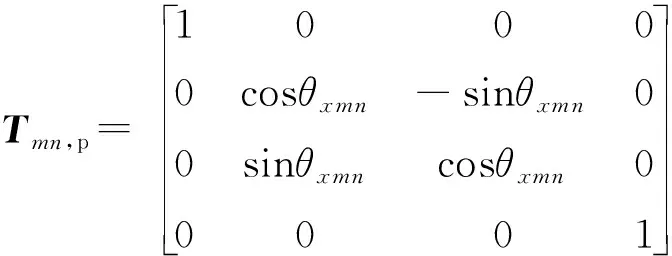
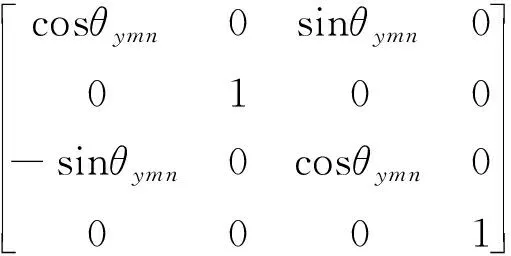
(2)
(3)

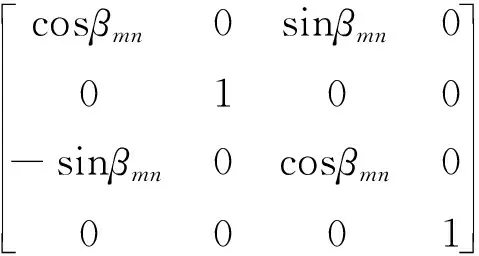
(4)
(5)
式中:amn,bmn,cmn为相邻体间的静止位置;θxmn,θymn,θzmn为静止角度姿态;xDH,yDH,zDH为运动位移误差;xDHmn,yDHmn,zDHmn为静止位置误差;εoxmn,εoymn,εozmn为静止角度姿态误差;xmn,ymn,zmn为运动位移;αmn,βmn,γmn为运动角度姿态;εxmn,εymn,εzmn为运动角度姿态误差。
2.4 误差建模
对数控滚齿机床进行几何误差建模,依次建立各体的坐标系,数控滚齿机床相邻体之间的误差利用滚齿机床的拓扑结构传递计算,进而得到刀具和工件的相对位置偏差,通过对此位置偏差进行计算,从而得到数控滚齿机床的几何误差模型矩阵。
2.4.1坐标系设立
设立0,1,2,3,4,5,6坐标系分别为床身坐标系(基坐标系)、立柱坐标系、滚刀主轴坐标系、滚刀坐标系、X向进给板坐标系、工件轴坐标系、工件坐标系。
2.4.2建模分析
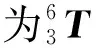
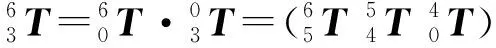
(6)
对YK3150E滚齿机误差进行分析,由于在运动过程中存在误差,因此坐标系3相对于坐标系6的变换矩阵为:
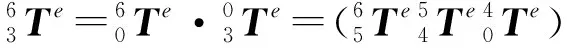
(7)
式中:e为运动过程中所存在的误差。在实际加工过程中,刀具坐标系3相对于工件坐标系6的变换矩阵为在理想情况下的变换矩阵上面叠加一个误差运动矩阵E,即:
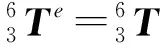
(8)
计算数控滚齿机每对相邻件的特征矩阵,使用齐次坐标转变法[5],将切削点在刀具坐标系3中的坐标,转变到工件坐标系6中。这两个坐标系中,当相对应的坐标轴之间的夹角小于0.5°时,转换矩阵将简写成以下形式,从而得到机床加工误差的几何数学模型为:
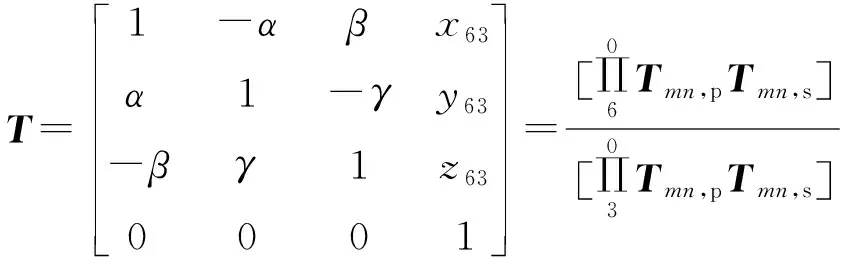
(9)
式中:x63,y63,z63分别为切削刀所在坐标系3对应被加工件所在坐标系6中沿X,Y,Z轴的运动位移误差;α,β,γ分别为刀具坐标系3绕工件坐标系6中Z,Y,X轴的回转角度误差。
3 误差模型数据解耦
上述得到误差几何数学模型是滚刀相对于工件的误差矢量,要想提高齿轮加工精度,需要得到各轴独立的进给误差补偿量,而滚刀和工件之间的误差矢量与各轴的误差补偿量间存在耦合关系,故需要对其进行误差解耦[6]。本文利用变系数微积分法,忽略运动误差影响,通过各轴补偿值的正负号,来确定补偿的方向,使其在进行误差补偿后,分离的滚刀坐标系3与工件坐标系6尽量重合,则存在以下函数关系:eT6,3·sT6,3=E,用sT6,3表示坐标系3相对坐标系6补偿运动变换的矩阵;eT6,3表示几何误差模型矩阵。由微分变换法可知滚刀坐标系3对于工件坐标系6的微分变换为:
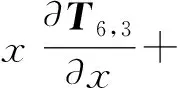
(10)
式中:ΔθB,ΔθC,Δx,Δy,Δz分别为旋转轴B、旋转轴C和X,Y,Z轴的补偿当量。
同时:
(11)
且:
eT6,3·sT6,3=E
(12)
sT6,3=T6,3+dT6,3
(13)
联立公式(10)~(13),可得YK3150E数控滚齿机床每一个轴的误差补偿量为:
δx=sinψ[y63-zcosψ(x-Q)]+
z[cosψsinφ(x-Q)/cosφ-cscψ]-cosψx63
(14)
δy=-x63sinψ-y63cosψ-
z[1+(x-Q)cos2ψ]-tanφ(x-Q)(1+zcos2ψ)/sinψ
(15)
δz=cscψ(x-Q)-z63
(16)
式中:Q为坐标系6相对坐标系3在X轴的偏离量;x,z为机床沿X轴、Z轴的运动位移;x63,y63,z63分别为坐标系6相对于坐标系3在X,Y,Z轴的运动位移误差;ψ为工件的转动量;φ为滚齿机加工斜齿轮时滚刀安装的角度。
将误差模型进行数据解耦后得到各轴件的误差补偿量,通过修改数控机床加工参数,对齿轮加工精度进行修正,从而提高了齿轮本身的精度。
4 结束语
随着制造业的飞速发展,齿轮加工、制造的水平也在逐步提高。YK3150E数控滚齿机床的加工精度对我国齿轮制造业的发展作用重大。本文通过多体系统理论研究法,建立机床拓扑结构,用低序体阵列对拓扑结构数字化描述,结合坐标变换法进行机床误差几何建模,从而分析了滚刀和工件之间产生的位置误差和旋转误差对齿轮加工精度所造成的影响,通过变系数微分法,对几何模型进行误差解耦,进一步得到机床各轴的误差补偿量,根据所得到的误差补偿量,可以对齿轮加工精度进行修正。这一研究对于提高齿轮的制造精度有着重要作用,同时也对研究数控滚齿机床误差补偿技术具有一定的借鉴意义。
