环形隔板结构参数对燃气弹射压力冲击平滑效果影响

程洪杰， 陈 力， 赵 媛， 刘 准

(火箭军工程大学 兵器发射理论与技术军队重点学科实验室，西安 710025)

燃气弹射因能有效减弱高温燃气流对弹体的烧蚀、冲击和振动，被广泛应用于国内外各种战略战术导弹的发射[1]。针对导弹燃气弹射，Edquist[2]解算了热力学参数的变化规律、能量方程和运动方程，袁曾凤等[3-4]建立和完善了经典零维内弹道理论。惠卫华等[5]用“半实验半理论”的方法得到了低燃温弹射过程的内弹道曲线，但无法获取弹射过程的空间流动细节。谭大成等[6]建立了自弹式弹射的二维轴对称数值模型，对弹射过程的流场特性进行了分析，忽略了燃气的多组分和富燃特性[7]。胡晓磊等[8-9]研究了低温弹射二次燃烧的反应机理以及对内弹道载荷和性能的影响，李仁凤等[10]得出弹射过程的初始压力冲击是由二次燃烧导致，二次压力冲击是由燃烧室总压升高导致的结论，并研究了二次燃烧产物对内弹道性能的影响。针对弹射过程压力双波峰冲击问题，胡晓磊等[11]通过在发射筒内增加环形腔有效平滑了压力曲线，但存在较大的冲量损失，同时在弹射后期引起较大的压力震荡和波动。李仁凤等[12]对比了有无壁面障碍物对燃气弹射载荷及内弹道性能的影响，但未进一步解耦分析障碍物结构参数对其的影响机理。

为更加有效地平滑压力双峰冲击，有必要优化障碍物的结构参数，使得弹底压力曲线变化更加平稳和高效。本文在以上研究的基础上，建立了包含导弹运动和二次燃烧的初容室二维数值模型，分析了环形隔板的主要结构参数对压力冲击平滑效果的影响机理，为弹射装置结构优化提供了参考。

1 物理模型和计算方法

1.1 物理模型

燃气弹射装置燃气发生器、导流锥、发射筒、导弹尾罩、底座以及支撑结构组成，几何模型如图1所示。其中，P点为实验和数值仿真监测点。弹射的物理过程为：低燃温推进剂在燃气发生器中燃烧产生高压气体，经喷管加速进入发射筒内迅速建立压强，同时与筒内空气发生剧烈二次燃烧加快建压过程，推动导弹向上运动。

图1 燃气弹射装置几何模型Fig.1 Geometric model of gas-ejection launcher

1.2 数值计算模型

1.2.1 控制方程

针对燃气弹射装置具有高度轴对称的特点，数值求解采用二维轴对称多组分Navier-Stokes(N-S)控制方程，具体变量含义参见文献[11]。

(1)

其中：

1.2.2 化学反应模型及湍流模型

采用能有效模拟初容室内二次燃烧现象的有限速率/涡耗散模型，其净反应速率Ri由Arrhenius化学动力学和涡耗散反应速率混合控制，Arrhenius反应速率作为动力学开关，阻止反应的的火焰稳定之前发生，延迟了计算中化学反应的开始，较为符合实际,被广泛应用于湍流扩散燃烧[13-15]。其中：

(2)

(3)

(4)

式中：YR为反应物质量分数；YP为燃烧产物质量分数；A和B为常数，分别取4.0和0.5；文中复燃模型均采用文献[15]中CO/H2两步反应：

2CO+O2→2CO2+Q4(Q4=565.95 kJ/kmol)
2H2+O2→2H2O+Q5(Q5=565.64 kJ/kmol)

湍流模型采用RNGk-ε模型，其湍动能k及湍流耗散率ε的输运方程表示为：

(5)

(6)

式中：k和ε分别为湍流动能和耗散率；μ为混合物黏性；ρk=1.0；Gk为由于平均速度梯度引起的湍流动能k的产生项；Gb为由于浮力引起的湍流动能k的产生项；σε=1.3;Cε1=1.44;Cε2=1.92。

该模型适合完全湍流流动，对高雷诺数的湍流计算具有较高精度，相对于标准k-ε模型考虑了平均湍动中的旋转及旋流流动情况，可以更好地处理高应变率及流线弯曲程度较大的流动，比较适合描述障碍物引起的流场中涡破碎、分裂及涡心迁移运动。受壁面限制的湍流流动的近壁面处理方法采用标准壁面函数。

1.2.3 网格模型及边界条件

本文数值模拟部分包括喷管、初容室及导弹尾罩的封闭运动区域，采用质量较高的结构网格，图2为弹射器轴对称面1/2网格模型，在喷管和筒壁面处进行网格加密，第一层网格厚度为0.5 mm，壁面y+值保持在100以内满足要求。导弹尾罩为运动边界，采用动态分层动网格技术，当网格节点位移超过预设高度后，网格实现分层分裂来模拟弹底的运动，运动规律由牛顿第二定律导出，运动方程参见文献[11]。

喷管入口采用压力入口条件，数据由自由射流实验采集得到[12]，总压曲线如图3所示，燃气发生器和喷管的壁面采用绝热壁面边界条件，发射筒壁面采用对流传热壁面边界条件。采用最小自由能法对推进剂燃烧产物进行热力学计算，得到喷管入口气体组分的含量和质量分数，如表1所示。计算初始状态为标准大气，静压为101.325 kPa，静温为300 K，发射筒内N2的质量分数为79%，O2的质量分数为21%。

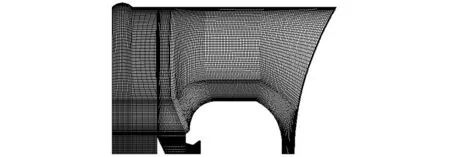
图2 网格模型Fig.2 Mesh model

表1 喷管入口组分及质量分数Tab.1 Species and mass fraction of nozzle inlet

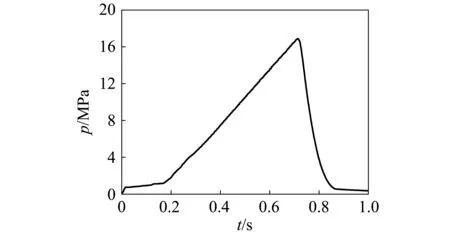
图3 总压曲线Fig.3 Curve of total pressure

1.3 数值求解方法

采用有限体积法对控制方程进行离散，求解方法采用压强-速度耦合算法，选择稳定性较好、计算速度较快的SIMPLE耦合形式。压力梯度项采用二阶格式离散，动量方程的差分格式均采用二阶迎风格式，湍流输运方程的差分格式采用一阶迎风格式，各项残差收敛精度为1×10-4，计算步长为4×10-5s。

2 网格无关性检验

对于包含多组分燃烧的非定常工程问题，数值计算的精度对网格大小和质量有较强的依赖性，因此有必要进行网格无关性检验[16]。选取2.19万、5.95万和9.97万三种网格密度进行弹射数值模拟，以监测点P压力和温度载荷作为比较对象，如图4所示。其中，p0为监测点的参考压力值，T0为监测点参考温度值，t0为参考时间值。

如图4可见，三种网格数量下P点的压力和温度载荷曲线具有相同的走势，相对误差不超过1%，考虑到计算效率的需要，选取2.19万网格作为计算对象。

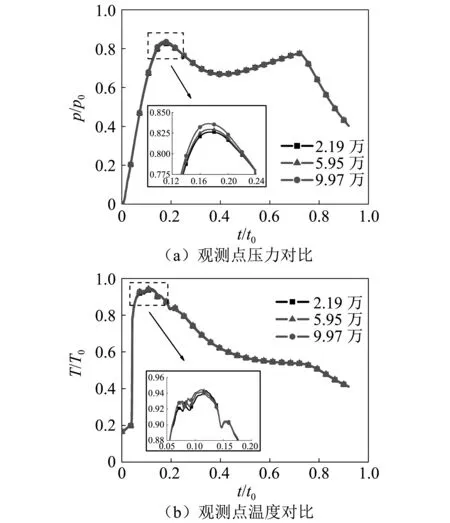
图4 网格无关性检验Fig.4 Mesh independence test

3 数值方法验证

为验证文中所建立数值模型及计算方法的可靠性，将数值计算结果与文献[12]飞行实验数据进行对比，监测点P的计算值和实验值对比如图5所示。对于初始压力波峰，实验值为0.83p0，计算值为0.84p0；对于二次压力波峰，实验值为0.78p0，计算值为0.79p0。对于温度波峰，实验值0.94T0，计算值为0.94T0。

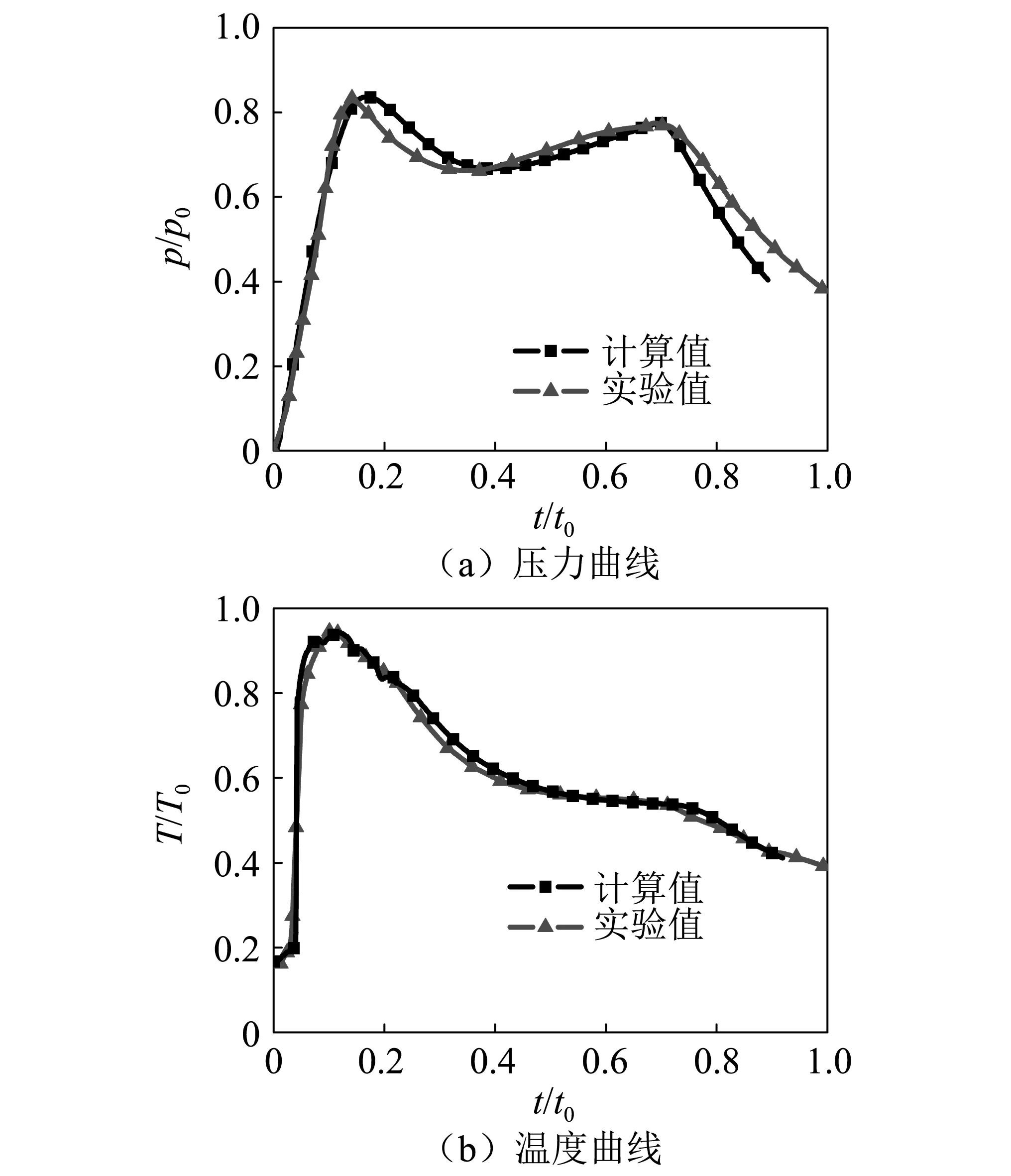
图5 P点计算值与实验值Fig.5 Calculation and experiment values at point P

易知，数值计算结果成功捕捉了弹射过程中两次压力冲击峰值和温度峰值，最大误差为1.2%，表明文中建立的数值模型和方法具有较高精度。

4 结果与分析

4.1 影响平滑效果的主要结构参数

为筛选出对压力冲击平滑效果影响较大的结构参数，现以隔板个数n=4、最下方隔板布置高度H=400 mm、最下方隔板高度h=300 mm、级差S=50 mm、间距s=200 mm为基准工况，对n，H，h，S和s五个结构参数进行解耦分析，弹底平均压力曲线如图6(a)～(e)所示。图7左侧为h=200 mm工况在0.1t0时刻的温度云图，右侧为h=300 mm工况在0.1t0时刻的温度云图。

由图6可见，随着结构参数的横向变化，图(a)、(b)、(c)和(e)压力曲线存在明显波动。如图6(c)和图7所示，最下方隔板高度为200 mm时，由于高度过低而无法有效阻挡燃气向上扩散，大量燃气绕过隔板，首先包围燃烧室壁面，再向尾罩和筒壁面方向运动，发生剧烈的二次燃烧现象，导致压力上升提前、峰值变大。当h在300～400 mm区间内，隔板高度对燃气起到了明显的阻挡作用，如图7所示，二次燃烧高温区域明显减小；如图6(c)可知，在此高度区间内，隔板高度对压力平滑作用影响变小。如图6(d)所示，隔板级差对压力平滑效果影响较小。

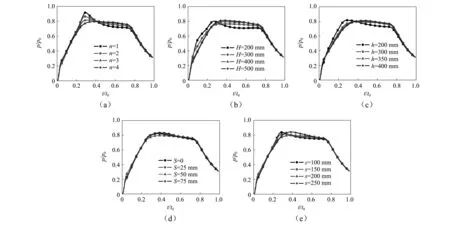
图6 5种结构参数下的压力曲线Fig.6 Pressure curves of 5 kinds of structural parameters

图7 0.1 t0时刻温度云图Fig.7 Temperature contour at 0.1 t0

综合上分析易知，n，H和s为影响平滑压力冲击效果的主要结构参数。

4.2 主要结构参数对平滑效果影响机理分析

4.2.1 隔板个数

以4.1中结构参数为基准工况，隔板个数为变量进行分析。图8为4种隔板个数下的O2质量分数曲线。图9为4种隔板个数在0.2t0时刻O2质量分数云图和流线图。由图6(a)和图8可见，在0～0.04t0时间段内，最下方隔板和导流锥下部区域氧气量充足，二次燃烧可以自由进行，导致4种工况的氧气质量分数快速下降，压力快速上升。

由图9可知，在0.04t0～0.2t0时间段内，发射筒下部区域氧气量基本消耗殆尽，燃气受到隔板阻挡，需经筒底壁面反射然后绕过隔板向上扩散，导致扩散速率变慢，压力上升速率和氧气质量分数下降速率变缓，如图6(a)和图8所示。

图8 4种隔板个数的O2质量分数曲线Fig.8 O2 mass fraction curves of 4 kinds of baffle numbers

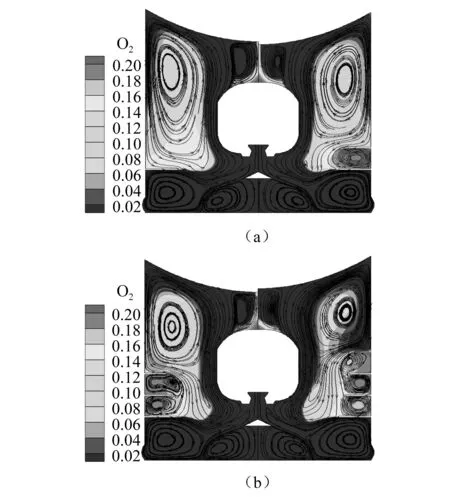
图9 0.2t0时刻O2质量分数云图和流线图Fig.9 Mass fraction contours of O2 and streamlines at 0.2t0

如图9所示，在0.2t0～0.3t0时间段内，随着隔板个数的增加，隔板腔储存的氧气量增加，参加二次燃烧的氧气量变少，氧气消耗速率变慢，压力冲击峰值变小。

如图6(a)所示，在0.3t0～0.75t0时间段内，随着尾罩的运动，发射筒的容积越来越大，对压力起到了“稀释”作用。同时，喷管入口总压迅速上升，喷入发射筒内燃气增多，建压速率变快；随着隔板个数增加，隔板腔内储存的氧气增多，持续发生二次燃烧增压效果也越明显。两方面的增压因素用来抵消压力的衰减，所以隔板个数越多，压力衰减越慢。n=4工况的增压速率基本上与压力衰减速率持平，平滑效果最理想。

在0.75t0至导弹出筒的时间段内，由于喷管入口总压开始下降，同时随着尾罩高速运动，发射筒容积不断变大，导致压力出现快速衰退。

综合分析可知，当n=1和2时，压力冲击波峰相对于无隔板时变得更大；当n=3和4时，隔板对压力冲击波峰开始显现平滑作用，其中n=4的平滑效果最佳。

4.2.2 最下方隔板布置高度

以4.1中结构参数为基准工况，最下方隔板布置高度为变量进行分析。图10分别为0.1t0时刻H为200 mm、300 mm、400 mm和500 mm的O2质量分数云图和流线图，图11为4种布置高度下的O2质量分数曲线。

由图10(a)流线图可见，H=200 mm工况的燃气经导流锥分流后，被最下方隔板“冲散”为三部分：第一部分在导流锥下部形成逆时针回流区，第二部分在隔板下部形成顺时针回流区；第三部分在隔板右侧形成顺时针回流区，向上扩散时，其中一部分向燃烧室壁面方向运动，形成一个逆时针的大涡，另一部分与隔板腔口的氧气发生二次燃烧，对腔内的氧气形成扰动，导致隔板腔内出现多个小涡。H为300 mm、400 mm和500 mm时，流场结构基本一致。

图10 0.1t0时刻O2质量分数云图和流线图Fig.10 Mass fraction contours of O2 and streamlines at 0.1t0

由于布置高度为200 mm与300～500 mm的流场结构不一致，导致二次燃烧扩散的轨迹和对隔板腔内渗透程度存在较大差别。如图11易知，二次燃烧的主要区域集中在隔板下部和燃烧室壁面附近，随着隔板布置高度的增加，隔板下部区域氧气量增加，但向隔板腔内渗透的燃气量变少，导致腔内储存氧气量增加。此消彼长，如图6(b)和图11所示，在300 ～500 mm高度区间，随着布置高度增加，氧气消耗速率变缓，这说明隔板腔储存的氧气增加量大于消耗量，中后期持续的二次燃烧相对剧烈，压力的峰值相应变大。

综合分析可知，最下方隔板布置过低时，氧气消耗速率变快，压力上升加快，且压力曲线出现较大波动，不利于导弹的平稳发射。随着最下方隔板布置高度的增加，压力峰值先减小后增加，布置高度为300 mm时，平滑效果最优。

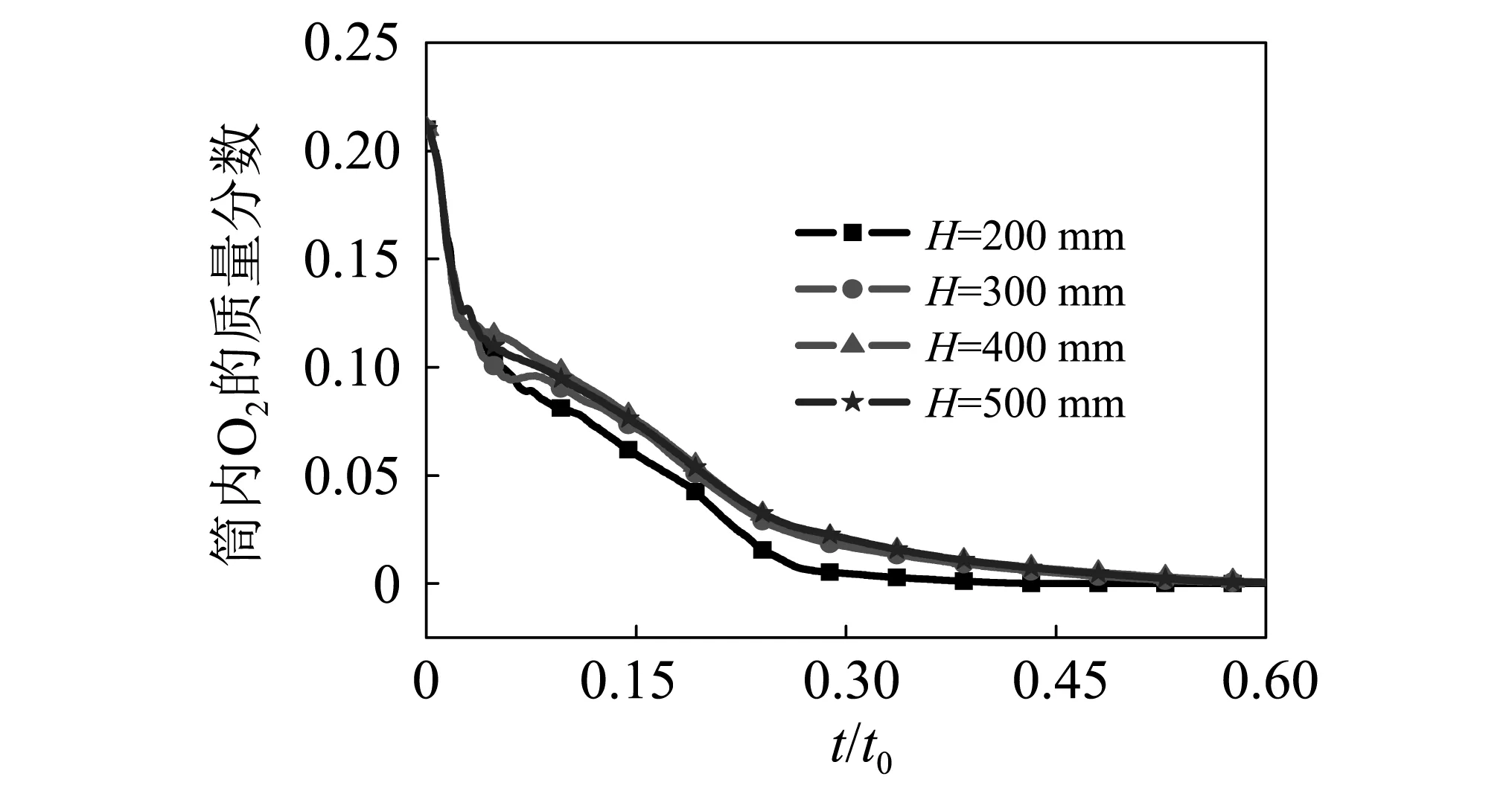
图11 4种布置高度下的O2质量分数曲线Fig.11 O2 mass fraction curves of 4 kinds of height

4.2.3 隔板间距

以4.1中结构参数为基准工况，隔板布置间距为变量进行分析。图12和图13分别为0.3t0时刻4种隔板间距下的O2质量分数云图和曲线。间距s在100～200 mm区间变化时，随着间距的增加，隔板腔内储存的氧气质量随之增加，燃气对隔板腔内的渗透程度也在上升，如图12(a)所示。由图13可见，在0.3t0时刻，发射筒内氧气质量分数呈递增趋势，这说明：随着间距增加，增加的氧气储存量大于燃气渗透加强而引起的氧气消耗量，从而导致前期参加二次燃烧的氧气量减少，压力冲击峰值逐渐变小，由0.837p0降至0.795p0，如图6(e)所示；中后期持续发生二次燃烧增压的氧气量多，压力曲线衰减变慢。

当间距由200 mm变化至250 mm时，在0.3t0时刻，增加的氧气储存量仍然大于燃气渗透加强而引起的氧气消耗量，但是在0.3t0～0.45t0时段内，s=250 mm工况由于腔口过大，二次燃烧迅速，导致储存的氧气量快速衰减到与其他3种工况一致，如图13所示。所以间距在200 ～250 mm变化时，隔板腔虽然有效减少了前期参与二次燃烧的氧气量，但由于腔口过大，中期氧气消耗过快，压力会继续上升，冲击峰值达到0.842p0，如图9(e)所示。此时环形隔板的布置仅仅起到了滞后压力冲击的作用，并未有效平滑压力曲线。

综合分析可知，隔板间距在100 ～250 mm之间变化时，压力峰值呈现先减小后增加的趋势，s=200 mm峰值最小，为最优的布置间距。

图12 0.3t0时刻O2质量分数云图Fig.12 Mass fraction contours of O2 at 0.3t0

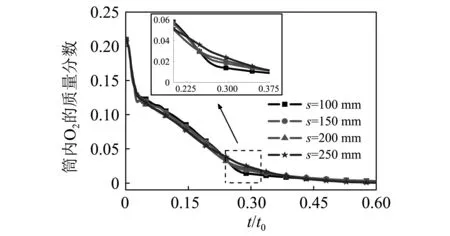
图13 4种间距下的O2质量分数曲线Fig.13 O2 mass fraction curves of 4 kinds of separation distances

4.3 内弹道特性分析

由4.2节分析，得到一组理想的环形隔板结构参数组合为：n=4，H=300 mm，h=300 mm，S=50 mm，s=200 mm。将其内弹道特性曲线与实验装置进行对比，如图14(a)～(c)分别为为导弹加速度、速度和位移变化曲线。a0为加速度参考值，v0为加速度参考值，l0为位移参考值。

由图14(a)可见，该结构参数组合基本达到了理想的加速度设计曲线，有效地平滑了加速度冲击，匀加速时长约为0.5t0，最大加速度由0.888a0减小至0.795a0，减小了10.5%。由图14(b)可见，无环形隔板时导弹出筒速度为0.916v0，布置环形隔板后出筒速度为0.911v0，降低了0.55%，满足设计出筒速度范围：0.8v0～ 0.95v0[10]。由图14(c)可见，无环形隔板时出筒时间为0.959t0，布置环形隔板后出筒时间为0.984t0，延迟了2.6%。

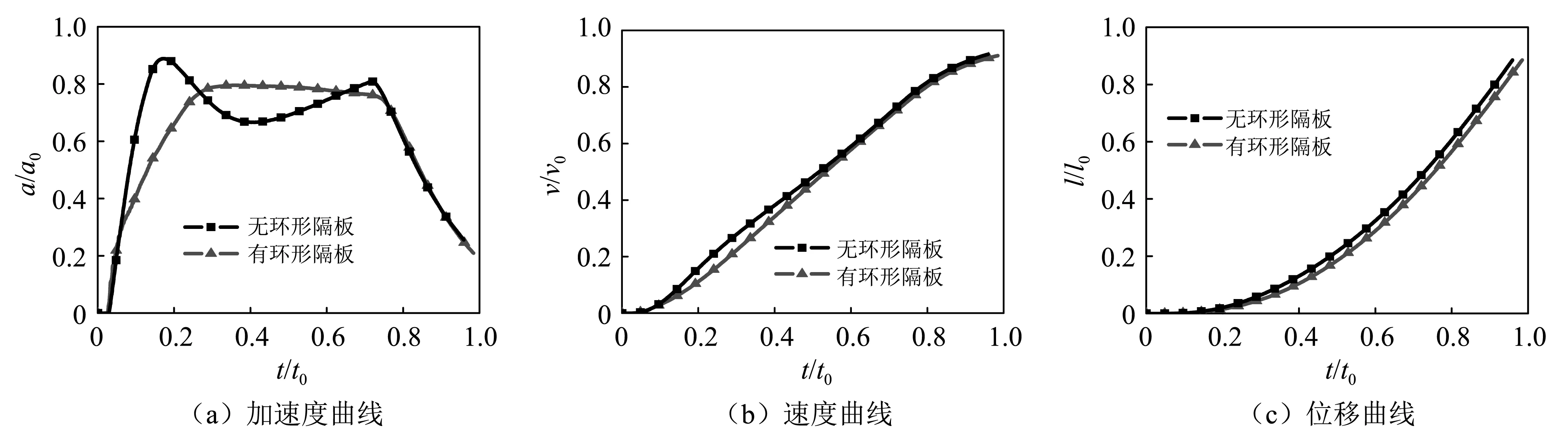
图14 内弹道曲线Fig.14 Interior ballistic curves

综上分析可知，合理地匹配环形隔板结构参数，可使加速度峰值减小，对压力冲击达到理想的平滑效果，使得导弹弹射过程更加平稳高效。

5 结 论

本文采用了RNGk-ε湍流模型和有限速率/涡耗散燃烧模型，建立了包含运动边界和二次燃烧的低燃温弹射数值流动模型，分析了环形隔板主要结构参数对平滑压力冲击效果的影响，得出如下结论：

(1) 从平滑机理上看，布置环形隔板可以延缓燃气向上扩散，同时储存氧气以减少前期参加二次燃烧氧气量，减小压力冲击峰值；储存的氧气在中后期持续发生二次燃烧增压，同时总压上升使得喷入筒内燃气增加，两方面的因素来抵消压力的快速衰减，从而平滑压力曲线。

(2) 隔板个数、最下方隔板布置高度和隔板间距为影响压力冲击平滑效果的主要因素。最下方隔板高度降至200 mm时，对平滑效果才会产生明显影响；隔板级差仅对压力峰值有较小的平滑作用。

(3) 隔板个数较少时，压力冲击增强，随着个数的增加，压力冲击逐渐减小，4个隔板时平滑效果最理想；最下方隔板布置过低时，压力曲线上升变快且存在较大波动，随着最下方隔板布置高度的增加，压力峰值先减小后增加，布置高度为300 mm时，弹底压力曲线逼近理想设计曲线；隔板间距在100～250 mm之间变化时，压力峰值呈现先减小后增加的趋势，200 mm为最优的布置间距。

(4) 隔板个数为4、最下方隔板布置高度为300 mm、最下方隔板高度为300 mm、级差为50 mm、间距为200 mm时，压力冲击能够得到有效平滑，导弹加速度峰值减小10.5%，出筒速度降低0.55%，出筒时间延迟2.6%。