基于3D瞬态流场计算的滑动轴承非线性油膜力分析

李 强， 张 硕， 许伟伟

(1. 中国石油大学(华东) 化学工程学院，山东 青岛 266580; 2. 中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580)

液体动压径向滑动轴承以其承载能力大、功耗小、运转精度高等优点广泛应用于汽轮机组、工业压缩机、核电机组及各类大型机床，是机械工业中使用广泛、要求严格的关键基础部件之一。

滑动轴承油膜力既是转子-轴承系统阻尼的主要来源，也可能是导致机组稳定性下降的重要原因，是否能准确获得非线性油膜力直接决定了转子-轴承系统非线性动力学分析的计算精度和效率。目前普遍采用的非线性油膜力计算方法主要有4类，一是解析或半解析方法，如将滑动轴承简化为无限长、无限短轴承油膜力模型[1-2]；二是采用有限元或有限差分法直接求解Reynolds方程[3-4]；三是基于Poincare变换的数据库方法；四是基于CFD的流场数值计算方法，其中前3类是基于Reynolds方程的方法。近年来，随着大型商用计算流体力学软件的出现，人们开始通过直接求解Navier-Stokes方程来研究滑动轴承的动力学行为。Chen等[5]利用CFD软件对滑动轴承、阶梯轴承、阻尼器等进行了稳态计算，讨论了在传统的求解Reynolds方程的方法中被忽略的惯性项、黏性项的变化对上述结构性能的影响；Lin等[6]利用CFD技术对转子-轴承系统的润滑性能进行了分析，详细讨论了轴承的热效应和空穴效应；Biswas等[7]利用FLUENT软件对气体润滑三油楔轴承进行了瞬态分析，并比较了不同时刻的压力和温度值；Panday等[8]利用FLUENT软件研究了滑动轴承的瞬态动力学行为，并计算了不同长径比下滑动轴承的承载力、摩擦力等；Li等[9]提出了基于FLUENT的滑动轴承流体模型和基于FORTRAN的多圆盘挠性转子动力学模型的耦合算法，并分析了轴颈倾斜对转子-轴承性能的影响。采用CFD建模计算，不仅可以考虑轴承内部的径向流场变化、流体惯性项的影响，对于事先未知的自由边界等问题更容易处理，理论上适用于任意轴承结构型式，因此基于CFD技术的3D流场计算方法越来越广泛地应用于滑动轴承性能的研究。

目前，滑动轴承3D流场计算最大的问题是，滑动轴承油膜流场在三个空间尺度上的尺寸大小非常不均匀，如果采用CFD软件中已有的动网格技术在轴颈移动几步后就会出现比较大的网格畸变，使瞬态流场无法继续计算[10-11]。为了准确计算滑动轴承非线性油膜力，通过研究，本文提出一种理论上适用于任何固定瓦滑动轴承瞬态流场计算的变流域动网格技术，保证了瞬态流场计算的顺利进行。在此基础上，本文首先计算并对比了小扰动下的线性和非线性油膜力，发现数值计算结果与理论分析一致，验证了数值计算方法的正确性；其次，通过对大扰动工况下滑动轴承油膜力的瞬态计算发现，大扰动工况下的转子-轴承系统非线性动力学分析有必要计入滑动轴承油膜非线性的影响；最后，在考虑了油膜力的非线性因素下，阐明了油膜力的切向和径向分量与滑动轴承稳定性的关系，以及瞬态润滑流场下油膜力分量的变化过程。

1 控制方程

FLUENT中所求解的连续性方程和动量方程对于可压缩和不可压缩流体的流动均适用。其中的动网格模型可以用来模拟由于边界运动引起的流域形状随时间变化的瞬态流动。

连续性方程为

(1)

动量方程为

(2)

(3)

式中：μ是流体黏度;I是单位应力张量; 式(3)右边第二项表示体积膨胀效应。

2 计算模型与方法

2.1 计算模型

本文主要对比讨论不同幅值的扰动载荷下油膜力的变化情况，而与具体的转子系统无关，因此计算模型简化为滑动轴承支撑下的单跨转子进行分析，计算模型如图1所示，应当指出，为了方便说明，轴承间隙被放大，其中转子的质量为M=17.527 kg。

图1 转子计算模型Fig.1 Schematic diagram of rotor

滑动轴承轴颈中心的运动方程为

(4)

式中：M为轴承承受转子的质量;e为偏心距;ω为转子角速度;Fx、Fy为油膜力在x,y方向的分力，是通过对油膜压力积分得到的，计算公式为

(5)

式中：R为转子半径;p表示压力;θ为压力与竖直方向夹角。

本文在进行非线性油膜力计算时，采用的滑动轴承模型如图2所示。

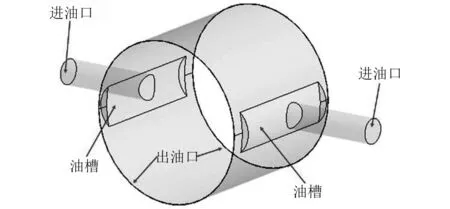
图2 滑动轴承计算模型Fig.2 Schematic diagram of journal bearing

为了与式(5)计算得到的非线性油膜力对比，下面给出线性油膜力计算公式

(6)

式中：Fx0、Fy0分别为静平衡位置时，油膜力在x,y方向的分量; [K]、[C]分别为刚度系数矩阵和阻尼系数矩阵。

图3 轴颈中心涡动时油膜力分量关系图Fig.3 Oil film force components at oil whirling

滑动轴承的动特性是与轴承内的流体动态力密切相关的，如图3所示。将油膜动压产生的力沿轴心轨迹分解，分为沿着轴颈涡动方向的切向油膜力Fτ和垂直轴颈涡动方向的径向油膜力Fr，计算公式为

(7)

式中：Ob为滑动轴承的中心；O′为轴颈的涡动中心； Δx、Δy分别为一个时间步内轴颈中心沿x和y方向的位移值。文中令切向油膜力的方向与轴颈涡动方向相同时为正值，径向油膜力以指向涡动轨迹曲率中心的方向为负值方向。

2.2 数值计算方法与边界条件

滑动轴承润滑流场为小间隙结构，径向间隙很小，尤其是在轴颈大偏心下，选用高阶精度的离散格式容易引起解的振荡而达不到收敛精度，而且应用本文的动网格方法可生成与流场适应的网格模型从而减轻低阶离散格式带来的假扩散现象。因此本文计算中，在保证计算精度的同时，为了提高计算速度和加快收敛，数值计算方法采用 “基于压力求解”，压力速度耦合方法，在稳态计算中为提高计算效率采用SIMPLEC算法，在非稳态计算中为了提高计算稳定性采用PISO算法，连续方程、动量方程采用一阶迎风格式，压力差值格式采用Linear差值，控制方程求解过程中考虑重力的影响，重力加速度设为竖直向下9.8 m/s2，忽略温度的影响[12-13]。

通过轴承润滑流场的尺寸和操作条件，可判定轴承流场处于层流状态；操作压力设为0 Pa，计算域的进口在两边进油口位置，边界类型为 “压力入口”，计算域的出口在轴承轴向的两端，边界类型为“压力出口”，出口位置的压力为大气压；轴颈面设为旋转面，稳态计算时直接指定旋转速度，动态计算时通过UDF指定旋转速度；固壁边界条件设置为无滑移条件，近壁面应用标准壁面函数。

2.3 转子-轴承系统耦合计算方法

转子-轴承系统的流固耦合计算采用弱耦合方法，计算流程图如图4所示。首先，基于FLUENT环境进行滑动轴承的三维瞬态流场计算，将计算得到的油膜压力通过式(5)获得滑动轴承瞬态油膜力并写入数据文件。其次，将得到的瞬态油膜力和转子参数代入式(4)可以得到当前时间歩内轴颈中心在x，y方向的加速度，进而求得速度和位移，并写入数据文件。最后，FLUENT通过自定义程序(UDF)调用上述轴颈位置参数完成轴承流域动网格更新和轴颈表面旋转速度的设置，然后进行下一个时间歩的计算，直至计算结束。

图4 瞬态转子-轴承系统计算流程图Fig.4 Transient calculation process of rotor-journal bearing system

3 动网格方法

在现有动网格技术的基础上，针对滑动轴承油膜间隙小的结构特点开发了适用于瞬态润滑流场计算的动网格方法，该方法中，网格节点的数量不变，节点间拓扑关系保持不变。

图5为轴颈扰动时，润滑流场中网格位置变化示意图。首先，选用六面体单元对滑动轴承润滑流场划分网格，保证润滑流场中每个节点的位置坐标都可以通过计算得到。当轴颈涡动时，流场最内圈上的所有节点都随着轴颈一起移动，最外圈及油槽上的节点保持不动，中间的节点按一定算法移动，如下式所示。

(8)

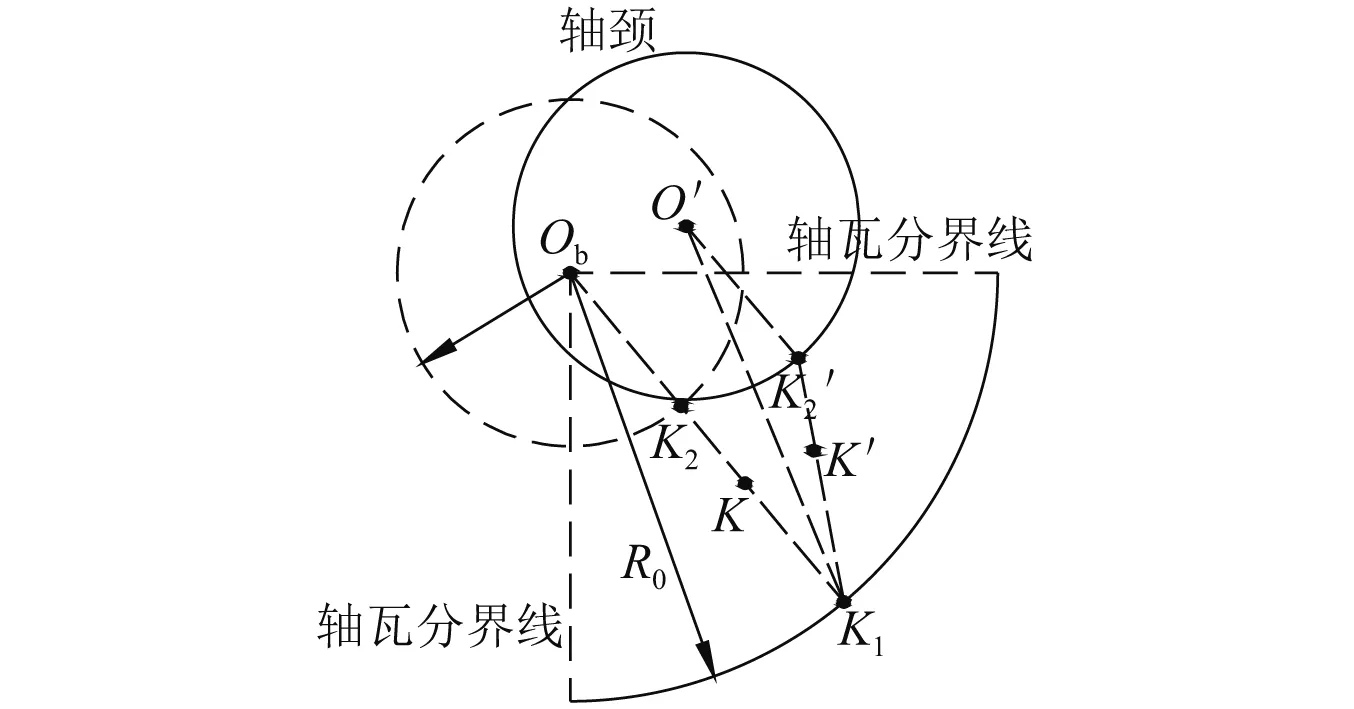
图5 轴承间隙周向网格移动示意图Fig.5 Mesh updating at radial clearance

该算法编程后可以通过UDF接口载入FLUENT中，并将节点移至新的位置，每完成一个时间步长的计算，就更新一次流域网格。通过大量的数值计算发现，通过该动网格方法移动后的网格即使在很大的轴颈偏心下依然能保证良好的光滑性和规整性，而且不容易出现负体积。

不同动网格方法更新结果如表1所示，由更新后的网格可以看出，FLUENT提供的三种动网格模型对滑动轴承小间隙模型的适用性较差，特别是大扰动情况下，难以保证计算稳定性、计算精度和效率。

表1 不同动网格更新方法比较Tab.1 Comparison of different dynamic mesh methods

4 滑动轴承的油膜力分析

当轴颈在静平衡位置受到扰动时，轴颈受到的油膜力和扰动之间的关系一般是非线性的。而当轴颈中心在静平衡位置附近作小振幅运动时，可以近似认为这种关系是线性的，本节对比分析了不同扰动幅值下的瞬态油膜力。

4.1 小扰动下油膜力分析

当转速取小于一阶临界转速的ω=800 rad/s，不平衡量取e=1 μm和e=2 μm时，计算得到的轴心轨迹如图6所示。从图中可知，当不平衡载荷较小时，轴心在静平衡位置附近做轨迹为椭圆的小幅度涡动，涡动的频率为转频，这与线性分析结果基本一致。

根据传统的润滑理论，小扰动情况下，随着不平衡量的增大，轴心轨迹和油膜力是以静平衡位置为中心呈比例增大。对应于图6轴心轨迹的线性油膜力和非线性油膜力的对比关系如图7所示。可以看出，当不平衡量e=1 μm时，线性油膜力与非线性油膜力一致性比较好，这时可以将系统进行线性化处理；当不平衡量增加到e=2 μm时，线性和非线性油膜力随时间的变化规律基本一致，但由于涡动中心地上移，使非线性油膜力和线性油膜力在位置上出现了偏移。

图6 轴心轨迹随不平衡量的变化Fig.6 Journal orbits for different unbalance

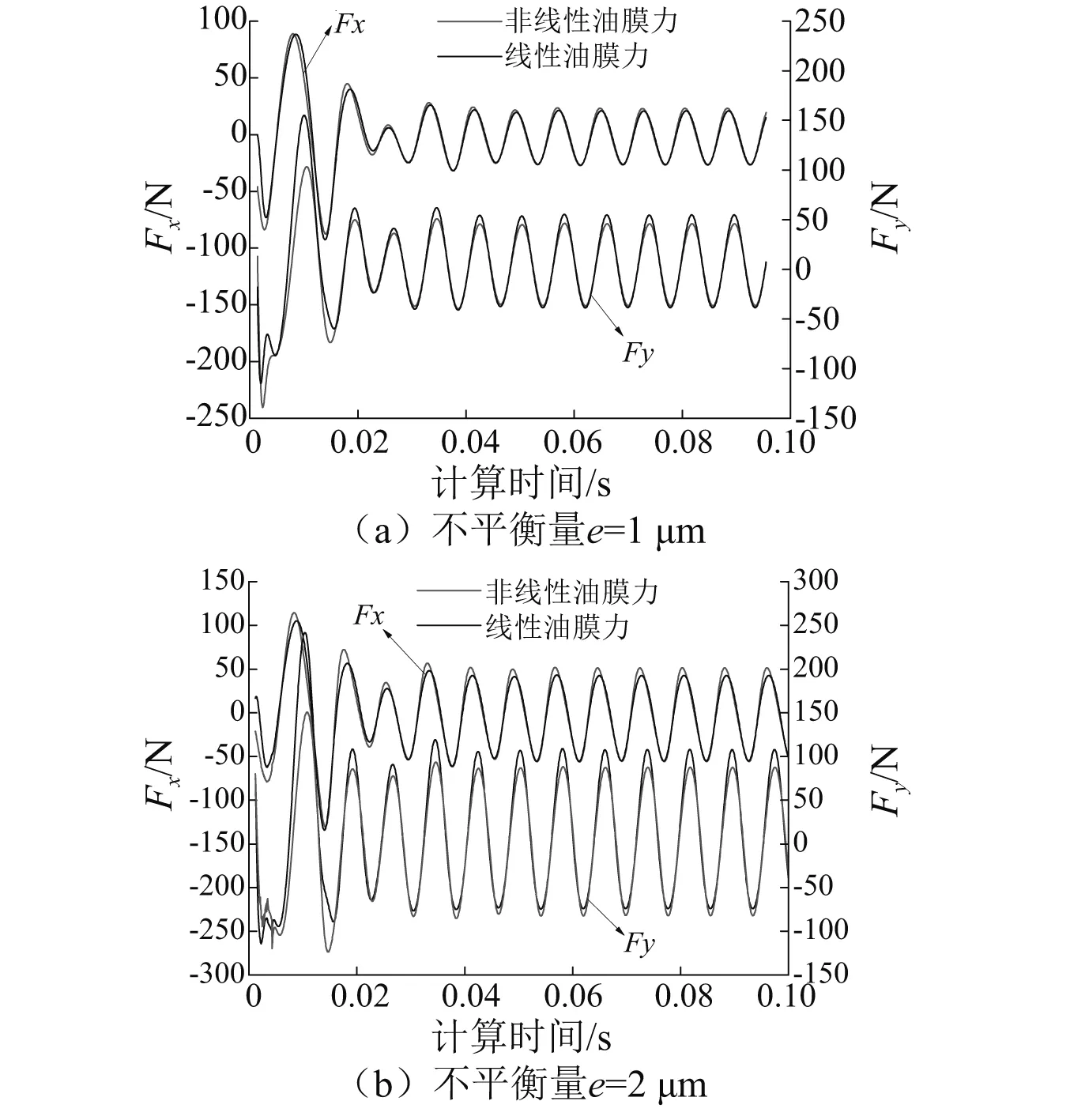
图7 小扰动下线性油膜力与非线性油膜力的对比Fig.7 Comparison of linear oil film force and nonlinear oil film force under small disturbance

4.2 大扰动下油膜力分析

图8和表2分别给出了不同扰动下滑动轴承的轴心轨迹和涡动中心的变化过程。从图中可知，当不平衡量较小时，轴心在静平衡位置附近作轨迹为椭圆的小幅度涡动，随着不平衡量的增加，轴颈振幅增大，轴心轨迹不再收敛于椭圆形状，且并没有一个固定的平衡位置，这时当不平衡量再变化时，轨迹的中心在变化，偏离了原来的静平衡位置，从轴心轨迹来看，即使转子的转速和轴承的静载荷都不变化，只要动载荷发生变化，轴颈的涡动中心也会随之改变，动载荷越大，涡动中心越靠近坐标原点位置。

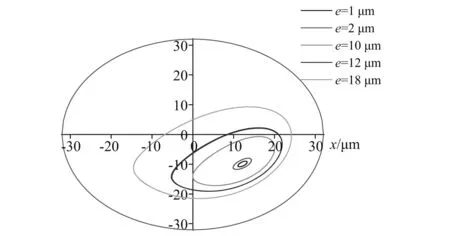
图8 油膜间隙对椭圆轴承轴心轨迹的影响Fig.8 Influence of oil film clearance on the journal orbits of elliptical bearing

传统的润滑理论认为，对于确定的转子-轴承系统，轴颈中心的静平衡位置决定于轴颈转速，即轴承的动力特性系数仅仅是轴颈转速的函数，因此关于滑动轴承动力特性系数的表格都是按照Sommerfeld数排列的，只考虑轴承参数、静载荷和轴颈转速的影响，而并没有考虑动载荷的影响。由上面对不同扰动载荷下轴心轨迹的计算可知，该结论在大扰动下并不成立。

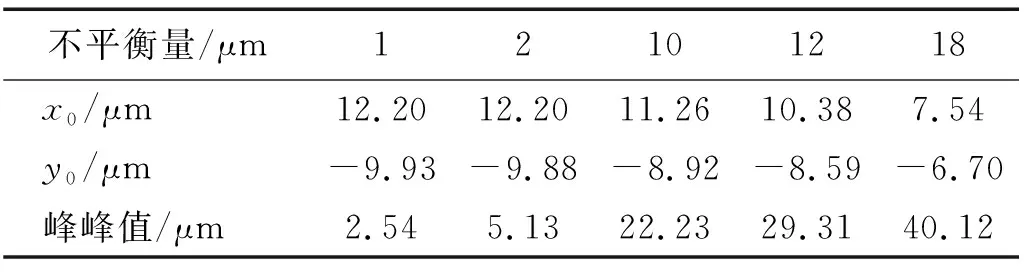
表2 滑动轴承的涡动中心随不平衡量的变化Tab.2 The whirling centers of the journal bearing with different unbalance

图9给出了大扰动下根据瞬态流场计算得出的非线性油膜力和线性油膜力的对比关系，从图中可以看出，根据静平衡位置处的动特性系数得出的线性油膜力与非线性油膜力差别明显，这时不只是两种油膜力曲线的位置不同，两种油膜力曲线的形状也产生了明显变化，此时不能再用线性模型来求解瞬态油膜力。因此在进行转子-轴承系统的非线性动力学分析时有必要计入滑动轴承油膜非线性的影响。

图9 大扰动下线性油膜力与非线性油膜力的对比Fig.9 Comparison of linear oil film force and nonlinear oil film force under large disturbance

4.3 瞬态油膜力的径向和切向分量

图10为转速ω=800 rad/s，不平衡量e=2 μm时轴心轨迹所对应的瞬态切向和径向油膜力，从图中可以看出，与油膜力分量Fx和Fy相比，瞬态油膜力的切向分量和径向分量更能反映轴承稳定性的好坏，当径向油膜力始终为负值时表明油膜的支撑刚度比较大，为轴颈提供足够的支撑而防止轴颈涡动轨迹变大；当切向油膜力始终为负值时表明系统阻尼足够大，使轴颈稳定涡动而不失稳。因此可以很容易从图10中切向油膜力和径向油膜力的大小判断出，当不平衡量e=2 μm时轴颈是以工频稳定涡动的。

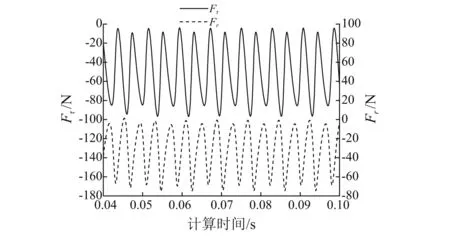
图10 滑动轴承瞬态油膜力分量Fig.10 Transient oil film force components of journal bearing

图11、12分别给出了不平衡量e=18 μm时不同的轴心涡动轨迹点对应的径向、切向油膜力和瞬态油膜压力场。当轴颈中心涡动到A点和B点附近时，受轴承右边油槽和进油口的影响，收敛楔的长度被大大缩短，降低了油膜的支撑刚度，表现为径向油膜力很小；当涡动中心继续向C、D点移动，虽然此时轴心在第二象限，但这时圆柱轴承的上轴瓦并没有形成明显的油膜收敛楔而产生大的油膜压力，反而随着轴颈中心的下移，逐渐在下轴瓦形成较大的油膜压力，这时由于整体油膜压力分布受油槽影响比较少，因此油膜支撑刚度比较理想，但涡动中心的位置比较靠上，形成的压力峰值比较小，导致切向油膜力比较小；随着轴颈涡动中心继续向E点移动，轴承左边油槽和进油口对油膜支撑刚度的影响慢慢变大，表现为径向油膜力有变大的趋势；但当轴心下移到F点附近时，由于这时轴心在x，y两个方向的偏心都比较大，形成了很大的油膜压力，而且F点距左油槽的距离明显比B点距右油槽的距离远，从压力云图上看，压力分布并没有明显的被油槽分割开，因此大的油膜压力使得这时切向油膜力和径向油膜力都比较大。

图11 e=18 μm时滑动轴承的轴心轨迹和瞬态油膜力分量Fig.11 Journal orbit and transient oil film force of journal bearing at e=18 μm

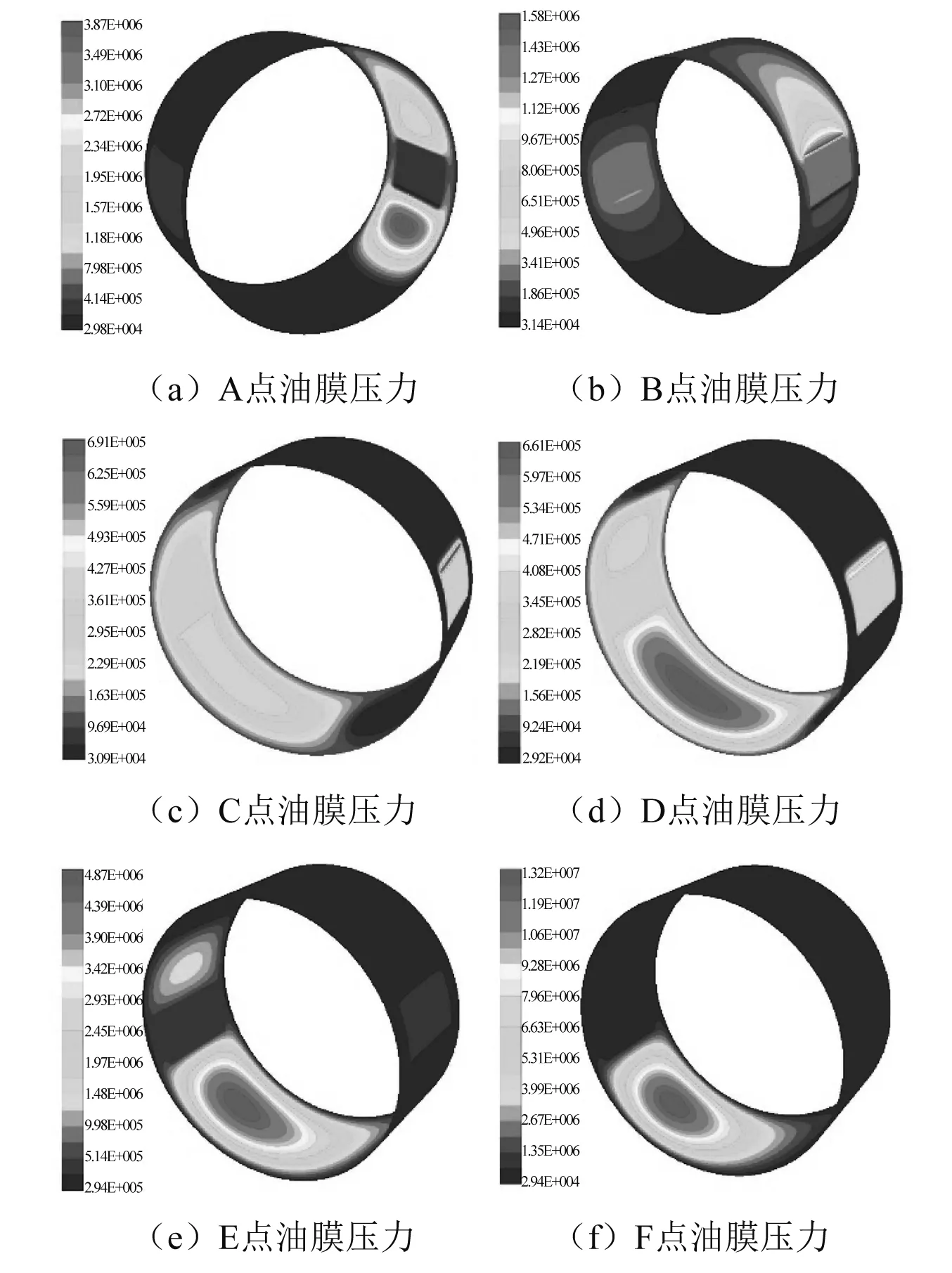
图12 e=18 μm时不同时刻轴颈油膜压力云图Fig.12 The pressure of oil film at different time at e=18 μm

为了研究半频涡动对切向油膜力的影响，令轴颈以相同的转速和不同的涡动频率作相同的涡动轨迹，得到的切向油膜力如图13所示。从图中可以看出，当涡动频率为转速的一半时，即轴颈进行半频涡动时，切向油膜力分量会变小，导致系统阻尼减小，容易引起系统失稳。因此当系统出现低频涡动时，系统的阻尼会大大降低而影响系统的稳定性。

图13 不同涡动频率时切向油膜力对比Fig.13 Comparison of tangential oil film force at different whirling frequencies

5 结 论

本文基于所提出的动网格方法对滑动轴承的3D瞬态流场进行了计算，得到以下结论：

(1) 所提出的动网格更新方法可在轴颈扰动时保持润滑流场网格节点间的拓扑关系不变，适用于大扰动下滑动轴承3D瞬态润滑流场的计算。

(2) 在小扰动情况下，线性和非线性油膜力随时间的变化规律基本一致，但大扰动工况下转子-轴承系统的非线性动力学分析，有必要计入滑动轴承油膜非线性的影响。

(3) 通过滑动轴承瞬态润滑流场的数值计算分析了滑动轴承切向和径向油膜力的变化过程。结果表明：进油口、油槽等对油膜径向力影响明显，显著降低了油膜刚度。

(4) 通过对比不同涡动频率下的切向油膜力，发现在半频涡动时切向油膜力相比同步涡动时显著降低，说明了当系统出现低频涡动时，系统的阻尼会大大降低而影响系统的稳定性。