弯扭耦合共振式振动时效的参激稳定性分析

2018-11-01蔡敢为黄院星黄逸哲李俊明

振动与冲击 2018年20期

蔡敢为，黄院星，黄逸哲，李俊明

(1.广西大学机械工程学院，南宁 530004； 2. 广西大学电气工程学院，南宁 530004； 3. 广西大学土木工程学院，南宁 530004)

振动时效是一种消减残余应力的有效方法，已经得到广泛运用。不论是低频的振动时效方式或超声波高频振动时效方式，要达到降低残余应力的效果，就要产生足够的动应力。时效的构件在振动应力和残余应力的共同作用下，产生局部的塑性变形，并释放残余应力[1]。目前在转轴类零件的振动时效工艺中，采用的是偏心电机激振法。受到偏心轮机构的限制，一般激振频率都小于200 Hz[2]。而对于要求结构尺寸稳定性较高的精密机床导轨、冷热轧钢机的辊轴，其低阶固有频率就很高，往往超过偏心电机的激振频率范围，采用传统偏心电机法难以使刚度较高的工件共振而产生足够的动应力。基于这个问题，蔡敢为等[3]提出了弯扭耦合共振式振动时效方法，通过弯扭耦合共振产生的动应力来消减具有较高刚度的转轴的残余应力。转轴在轴承的支撑之下由电机驱动旋转，当转速等于弯曲固有频率与扭转固有频率之差时，转轴处于共振状态，当转轴受到一个频率等于弯曲固有频率(或扭转固有频率)的横向激励(或扭矩激励)，弯曲共振与扭转振动相互加强。产生的动应力作为残余应力降低的驱动应力，不需要偏心电机激振方式。袁清平[4]指出，弯扭耦合的共振往往发生在弯曲振动和扭转振动的临界转速之和或之差处，然而振动信号的最高幅值是极其微小的。也就是说，即使转轴发生了弯扭耦合共振，振动的强度受到实际情况的影响，如转轴的刚度很大，其振幅是很小的。要产生大的振幅和动应力，需要在固有频率处施加激励，使得弯曲共振和扭转共振相互加强[5]。Perera[6]建立了基于集中质量模型的转子-轴承弯扭耦合动力学方程，并说明方程是耦合的、非线性的，他得出结论：当偏心转子以旋转频率ωr旋转，并受到一个频率为ωt的扭转振动激励，将产生频率为|ωr±ωt|的弯扭耦合振动，这个耦合振动可在转轴的固有频率处产生共振。Fujiwara等[7]推导了一个2自由度系统的弯扭耦合动力学方程，他认为，当旋转频率等于弯曲固有频率与扭转固有频率之和或差时发生弯扭耦合共振；此时，当转轴受到一个频率为弯曲固有频率(或扭转固有频率)的激励，将产生很大的扭转振动(或弯曲振动)。王小立[8]认为，弯曲振动与扭转振动之间的相互影响很小，在转速等于弯曲固有频率与扭转固有频率之和或差时，当施加的外激励力或扭矩等于弯曲或扭转固有频率时，将产生强烈的共振。由此可见，采用弯扭耦合共振进行振动时效是可行的。

对于弯扭耦合振动的分析中，Hsieh等[9-10]采用增量传递矩阵法分析弯曲振动与扭转振动的耦合关系,而传递矩阵法仅能得到位移响应，不能进行动应力的分析。传递矩阵分析复杂模型时，不便于进行子系统间的耦合分析[11]。连续模型才能进行动应力的分析，有限元法就是一种连续质量模型，已得到广泛应用。张勇等采用了连续质量模型推导出弯扭耦合偏微分方程组，得到了弯扭耦合振动的性质，而描述连续弹性体的动力学方程是高阶偏微分方程组，求解比较困难。

由于刚度、质量和阻尼参数的周期时变性，许多机械系统的动态特性可以采用含周期系数的二阶微分方程(组)描述，这些系统在力学上被成为参数振动系统[12]。如果在一个转子系统中存在有不对称的质量分布或者不对称刚度，通常这些不对称的参数将给线性微分方程引入周期性的时变系数，这种被称为参数激励的结果是，在转子的许多转动频率范围内，转子运动是不稳定或欠阻尼的[13]。如果转子承受周期扭矩作用且必须考虑弯扭耦合，均为周期参数激励系统，在某些转速范围内将发生失稳现象[14]。弯扭耦合共振式振动时效时转子-轴承系统的振动正是属于这种情况，因此有必要对其稳定性进行分析。郭红等[15]采用Routh-Hurwitz准则对单质量弹性对称系统进行稳定性分析。Yuan等[16]采用Floque理论分析了基于Jeffcott集中质量模型的转子系统弯扭耦合振动的稳定性，只能进行定性分析。对于转子-轴承系统，有必要采用多自由度的连续模型进行定量分析。弯扭耦合共振系统的动力学方程中含有时变系数,因而该系统动力学问题也属于参数振动的范畴。参数振动是一种特殊的振动形式,它的数学模型不一定是非线性微分方程,也可能是线性的,但系数不是常数,而是时间的周期函数,因此不属于线性振动理论的研究范围,也作为非线性的组成部分[17]。虽然参数激励系统不包含自由度的强非线性项，但由于系统中引入了无穷维时间项，学术上常将参数激励系统归类于非线性系统加以分析和研究[18]。含有参数激励的系统属于非自治系统,进行稳定性分析时就不能简单地用系统特征值实部的正负来判断了。

本文采用弯扭耦合共振理论进行对振动时效的转子-轴承系统进行研究，采用有限元方法对其进行建模，通过模态分析、瞬态动力学分析获得共振条件、动力学位移响应和动应力响应，在此基础上对弯扭耦合时变微分动力系统进行了稳定性分析。

1 有限元模型

转子-轴承系统包含转轴、轴承、刚性圆盘，如图1所示。转轴模型采用Timoshenko梁理论，即考虑剪切变形和转动惯量的影响，并包含陀螺力矩效应。转轴全长1.3 m，划分为13个等长度的梁单元，每个节点5个自由度，忽略轴向自由度，总共70个自由度。转轴直径为0.10 m。圆盘1位于节点3，内径为0.10 m，外径为0.24 m，厚度为0.05 m；圆盘2位于节点6，内径为0.10 m，外径为0.40 m，厚度为0.05 m；圆盘3位于节点11，内径为0.10 m，外径为0.40 m，厚度为0.06 m。节点P 位于节点8和节点9之间的中心截面上。转轴和圆盘的材料属性为：密度为7 800 kg/m3，弹性模量为200 GPa，泊松比为0.3。两个轴承分别位于节点1和节点14。轴承的刚度系数为Kyy=5×107N/m，Kzz=7×107N/m，阻尼系数为Cyy=500 Ns/m，Czz=700 Ns/m。对于转子-轴承动力学方程，具有5个自由度的转轴单元、圆盘单元和轴承单元的质量矩阵、刚度矩阵和阻尼矩阵参见文献[19]，可以很方便地将它们组集为整体矩阵。

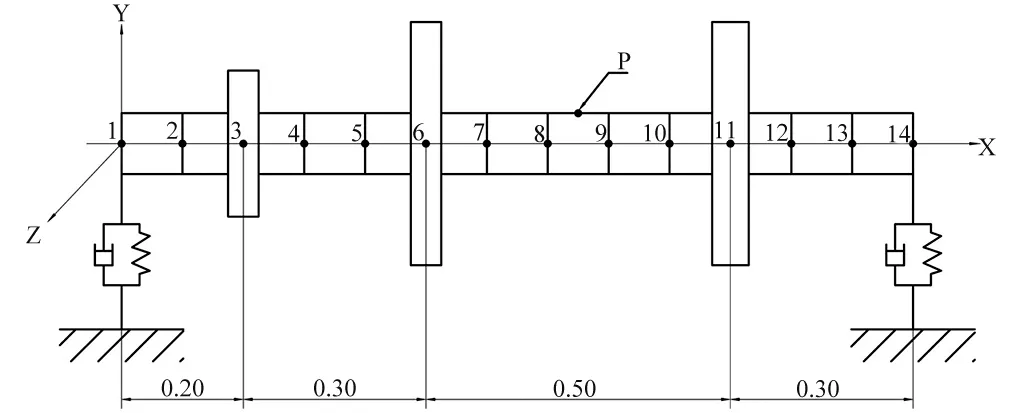
图1 转子-轴承系统有限元单元模型Fig.1 Rotor-bearing system finite element model

然而，由这些矩阵还不能得到转速、弯曲固有频率、扭转固有频率三者之间的和差关系。要得到弯扭特性，需要加入产生耦合的因素，本文加入的耦合因素是偏心质量。当旋转速度为Ω时，一个偏心距离为e、质量为mu的偏心质量的动能方程为[20]

(1)

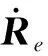
将偏心质量的动态矩阵添加到文献[19]的动力学方程中，得到偏心转子-轴承系统的弯扭耦合动力学方程

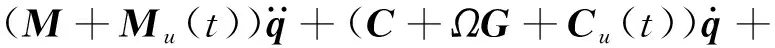
(2)

式中：M、K、C、G、q和分别为无偏心转子-轴承系统的质量矩阵、刚度矩阵、阻尼矩阵、陀螺矩阵、位移向量，F(t)为周期激励力向量。由于Mu(t)、Ku(t)和Cu(t)是时变矩阵，方程(2)代表的是一个参数激励系统。由有限元法建立的这一动力学方程是多自由度的连续模型，可以进行定量分析。

2 模态分析

考虑陀螺力矩的整体矩阵不再是对称矩阵，无法用求解大型稀疏矩阵的方法来进行模态分析，而用QRdamp法来提取模态参数。此时，需要求微分方程(2)的齐次解，即不考虑系统的广义力，令F(t)=0且无偏心质量，方程(2)变为

(3)

(4)

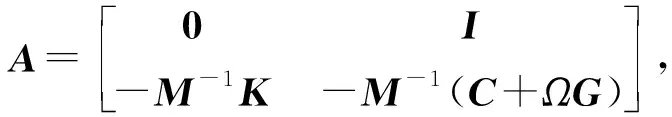
文献[21]对图1所示的转子-轴承系统进行了模态分析，转轴每个节点仅4个自由度，且未考虑剪切变形。为验证本文模型建立的正确性，求解25 000 r/min转速下的固有频率并与文献[21]进行对比，如表1所示。

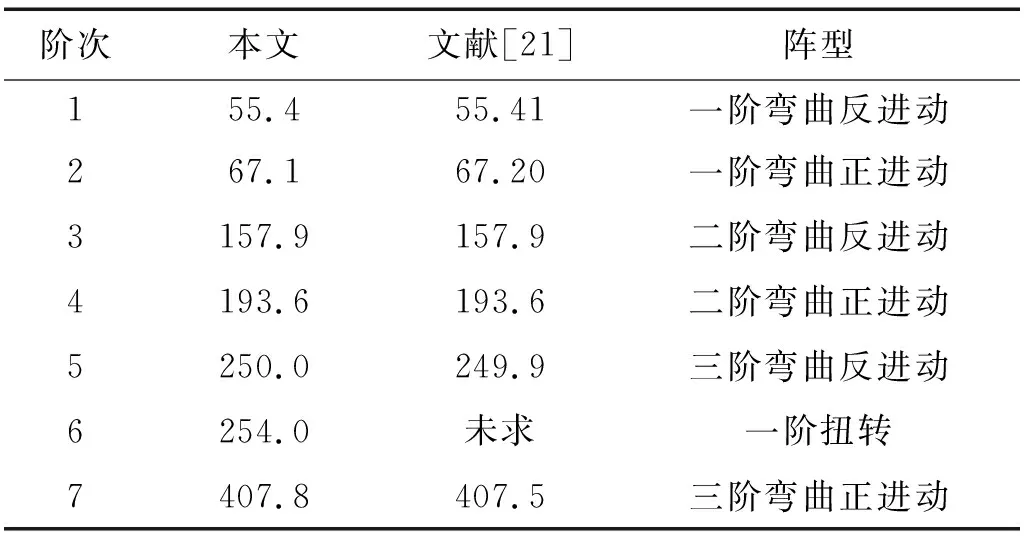
表1 转轴-轴承系统的固有频率Tab.1 Natural frequency of the rotor-bearing system Hz

由于文献[21]未求得一阶扭转固有频率，本文采用ANSYS APDL来求解，得到第一阶扭转固有频率阵型如图所示。

图2 第一阶扭转阵型Fig.2 The second order torsional mode shape

由图2可以看到，ANSYS APDL计算得到的第一阶扭转固有频率为254.5 Hz，与MATLAB有限元计算结果254.0 Hz的相对误差约为0.2%，综合以上计算结果表明本文建立的有限元模型是正确的。

而弯扭耦合共振式振动时效并不需要这么高的转速，根据残余应力所处的位置，选取合适的阵型，将弯曲固有频率与扭转固有频率之和或之差的频率作为旋转频率。为了更容易实现共振，取弯曲固有频率与扭转固有频率的差值。

3 瞬态动力学分析

3.1 位移响应

对参数激励系统，同样可以采用Newmark法来进行瞬态动力学求解，得到各节点的位移时域响应，再进行傅里叶变换，得到该节点的位移频域响应。下面用两个非共振情况和两个共振情况的瞬态动力学分析来说明哪种情况适合用来进行振动时效。激振参数如表2所示。

表2 激振参数Tab.2 Excite parameters Hz

各种情况下的扭矩幅值均为36 Nm，mu=0.2 kg，e=0.01 m。

3.1.1 非共振情况

对于非共振情况，可以施加任意的扭振频率和旋转频率。使用Newmark法计算得到转轴上节点8处Y方向的弯曲振动响应、扭转振动响应和轴心轨迹，分别如图3～5所示。

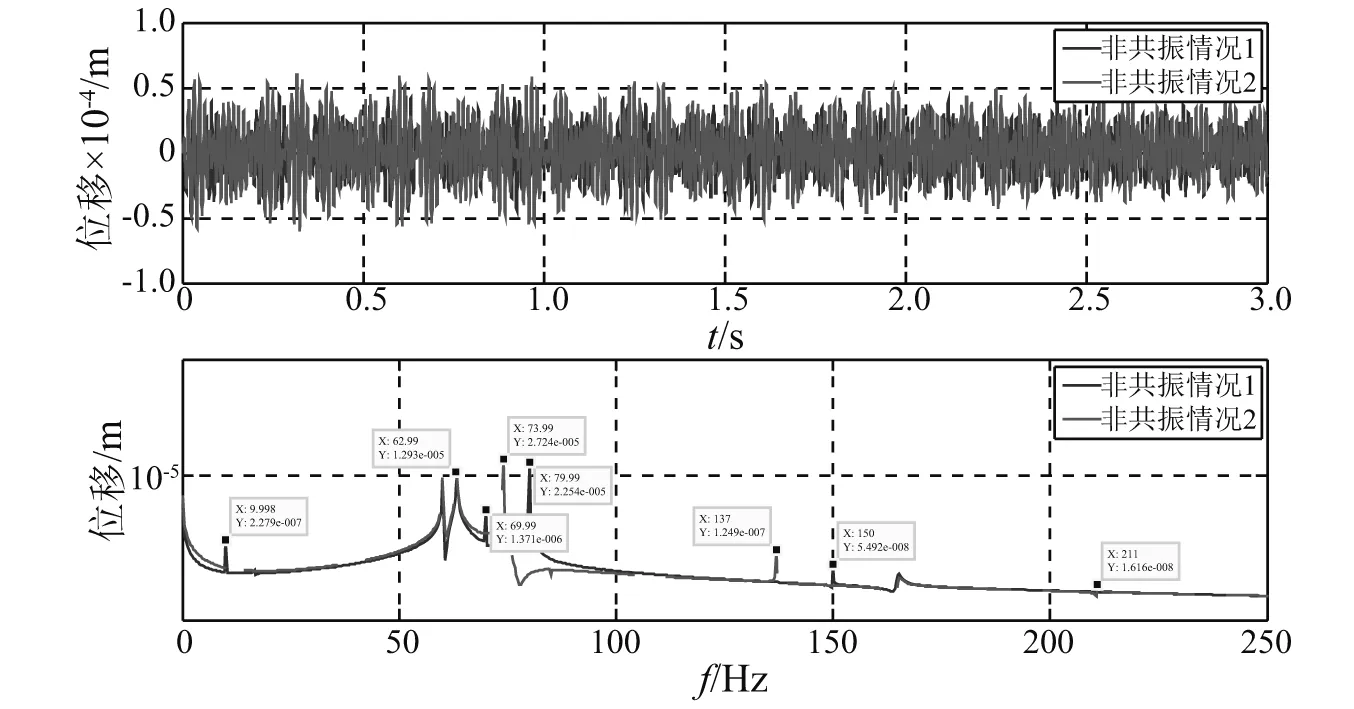
图3 非共振情况弯曲振动的时域响应和频域响应Fig.3 Time and frequency domain response of bending vibration in non-resonant situation

图4 非共振情况扭转振动的时域响应和频域响应Fig.4 Time and frequency domain response of torsional vibration in non-resonant situation

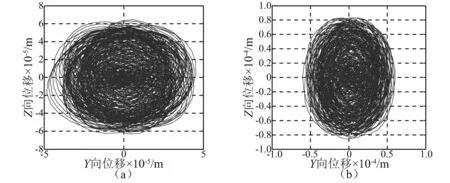
图5 非共振情况轴心轨迹Fig.5 Axis obit of non-resonant situation

对于非共振情况1，图3的70+80=150和80-70≈9.99是产生的耦合弯曲振动频率；对于非共振情况2，图3的137+74=211和137-74≈62.99是产生的耦合弯曲振动频率。耦合频率的出现说明弯扭耦合振动已经被激发，是弯扭耦合振动的一个特有现象。图5中的轴心轨迹表示转轴上节点8随时间变化走过的路线。图3的79.99≈80和73.99≈74均为与旋转频率同步的弯曲振动响应；图4的69.99≈70和137均为施加的扭转振动频率。然而，在图3的弯曲振动响应中，具有与施加的扭转振动频率相等的弯曲振动响应69.99≈70和137，说明扭转振动对弯曲振动产生了影响。实际上，弯扭耦合共振中弯曲振动与扭转振动是相互影响的，只是在不同的模型里有不同强度的体现。

3.1.2 共振情况

共振情况的扭转振动激励的频率等于第一阶扭转固有频率254.0 Hz。对于共振情况1，根据矩阵A求得转速为4 090 r/min的第二阶弯曲固有频率为185.9 Hz，第一阶扭转固有频率为254.0 Hz，此时他们的阵型如图6所示，将两个数值的差值254.0-185.9=68.1 Hz设定为转轴的旋转频率。

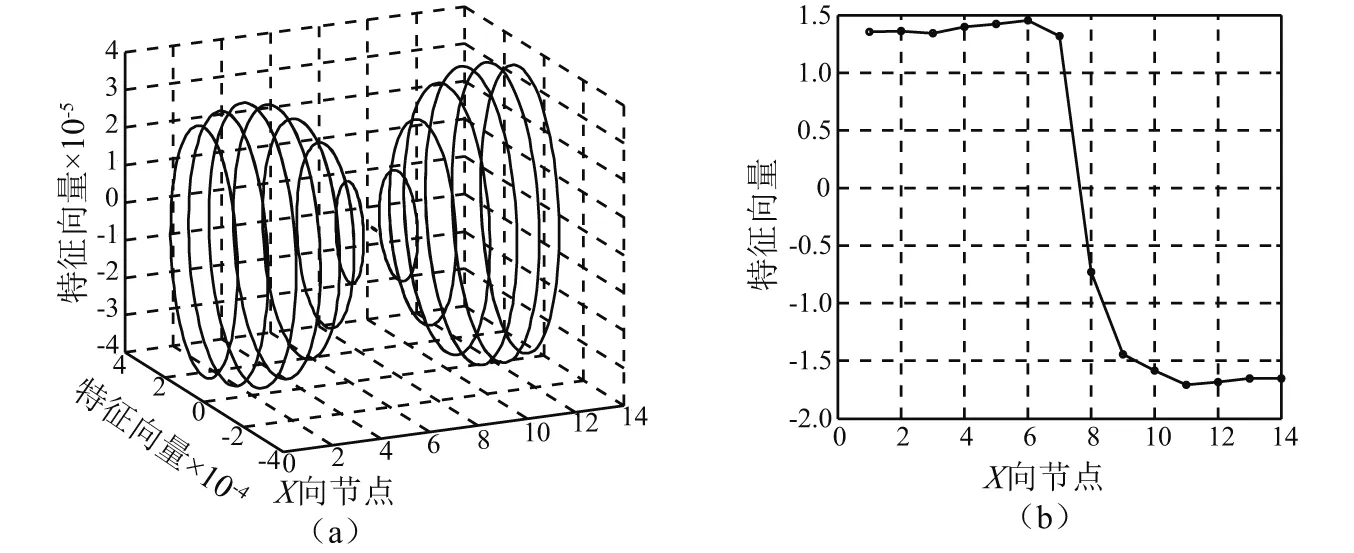
图6 转速为4 090 r/min下的弯曲和扭转阵型图Fig.6 Model shape at 4 090 r/min

对于共振情况2，根据矩阵A求得转速为11 364 r/min之下的第一阶弯曲固有频率为64.6 Hz，第一阶扭转固有频率为254.0 Hz，此时他们的阵型如图7所示，将两个数值的差值254.0-64.6=189.4 Hz设定为转轴的旋转频率。

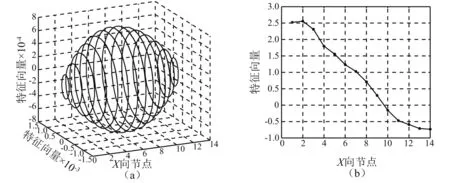
图7 转速为11 364 r/min下的弯曲和扭转阵型图Fig.7 Model shape under 11 364 r/min

使用Newmark计算得到转轴上节点8处Y方向的弯曲振动响应、扭转振动响应和轴心轨迹，分别如图8～图10所示。

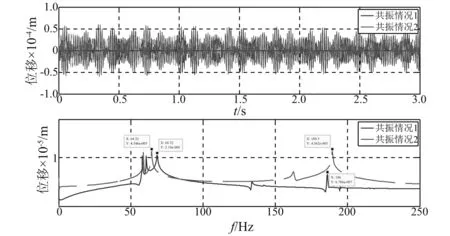
图8 共振情况弯曲振动的时域响应和频域响应Fig.8 Time and frequency domain response of bending vibration in resonant situation

图8中的254.0+68.17=322.17不在显示范围内， 254.0-68.17=185.83≈186是产生的耦合弯曲振动频率， 68.32≈68.17是同步弯曲振动响应。

图8中的254.0+189.4=443.4不在显示范围内， 254.0-189.4=64.6≈64.32是产生的耦合弯曲振动频率， 189.3≈189.4是同步弯曲振动响应。

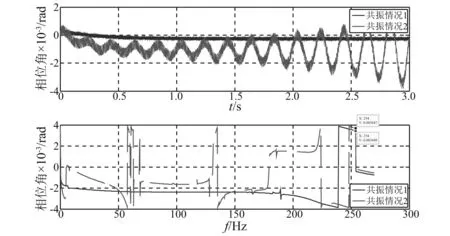
图9 共振情况扭转振动的时域响应和频域响应Fig.9 Time and frequency domain response of torsional vibration in resonant situation

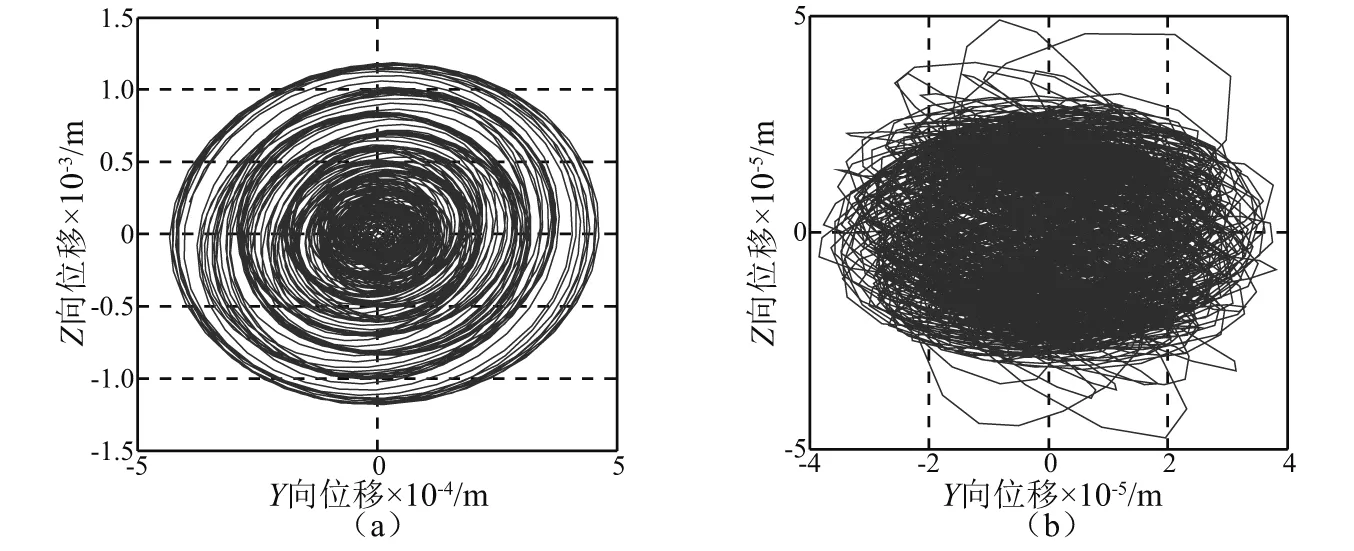
图10 共振情况轴心轨迹Fig.10 Axis obit of resonant situation

这些频率的出现说明弯扭耦合共振已经被激发。现在可以观察到弯扭耦合的现象：在同步激励的情况下，4 090 r/min的转速会产生4 090/60=68.167 Hz的同步弯曲振动，而不会产生186 Hz的弯曲振动。但是由于弯扭耦合，图8中的186 Hz是在4 090 r/min下由非同步扭振激励产生的耦合弯曲振动频率，将激起第二阶弯曲共振。在图9中，产生的扭转振动频率254.0 Hz将激起第一阶扭转共振。在同步激励的情况下，11 364 r/min的转速会产生11 364/60=198.4 Hz的同步弯曲振动，而不会产生64.32 Hz的弯曲振动。但是由于弯扭耦合，图8中的64.32 Hz是11 364 r/min下由非同步扭振激励产生的耦合弯曲振动频率，将激起第一阶弯曲共振。在图9中，产生的扭转振动频率254.0 Hz将激起第一阶扭转共振。弯曲共振和扭转共振相互加强，这种现象即为弯扭耦合共振。拍振现象明显，也是弯扭耦合共振被激发的一个现象。

比较非共振情况和共振情况可知，共振情况的振幅大于非共振情况。如图10所示，由于轴承两个方向的刚度不同，轴心轨迹是椭圆形的，共振情况1的运动轨迹比较平稳，而且采用的转速为弯曲固有频率与扭转固有频率的差值，数值更小，更适合用来进行振动时效。

3.2 动应力响应

由于横向转角很小，忽略横向剪切变形，转轴单元的应变可以由如下几何方程求得

(5)

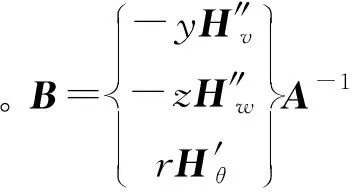
(6)

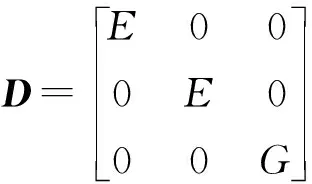
对于共振情况1，先求解节点8和节点9的位移响应，通过几何方程和物理方程就可以求出P点的弯曲和扭转动应力，再由第四强度理论求得Von Mises动应力，如图11所示。如果偏心距为零，弯曲和扭转不耦合；如果圆盘1的偏心距为0.002 kg·m，弯曲和扭转弱耦合；如果圆盘1和圆盘2的偏心矩均为0.020 kg·m，弯曲和扭转强耦合。

耦合的程度依赖于偏心矩mu×e的大小，通过调节偏心距离的大小和驱动电机的扭振幅值来产生足够的动应力。如图11中无耦合系统的动应力很小，约为0.1 MPa; 如图11中弱耦合系统的动应力约为5 MPa; 如图11中强耦合系统的动应力约为130 MPa。如果动应力与残余应力的叠加值超过材料的屈服极限，材料内部将产生塑性变形，残余应力将得到降低。弯扭耦合共振产生的复合正应力和切应力，使得残余应力的降低更加均匀。

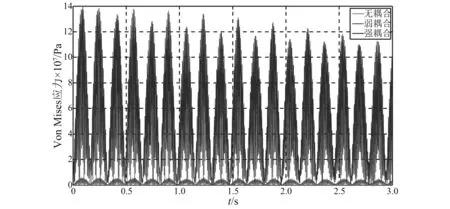
图11 动态Von Mises应力Fig.11 Dynamic Von Mises stress

4 稳定性分析

偏心质量随转轴一起旋转，造成偏心激励，同时，转轴承受到外部交变力矩作用，由前言描述可知有必要进行稳定性分析。对于参数激励系统，可以通过Floquet理论[23-24]来求解。周期解的稳定性分析关键是求解状态转移矩阵Mo，文献[25]列出了几种求解状态转移矩阵的方法，包括打靶法、Newmark法和切比雪夫多项式法等，因前文已用Newmark法进行位移和应力的计算，为采用Newmark法对方程(2)进行稳定性分析打下基础。计算的流程图如图12所示。

图12 稳定性计算流程图Fig.12 Flow chart of stability calculation

转轴具有70个自由度，因此系统整体矩阵的维数为70×70。状态矩阵的维数与系统整体矩阵的维数相同，设初始位移矩阵Ua为70×70的单位矩阵，依次求解Mo的1到70列，每次迭代的初始值取单位矩阵Ua的一列。周期T=2π/Ω，Ω为转轴旋转角速度，数值为弯曲固有频率与扭转固有频率的差值。时间步长取T/512，每个旋转频率下，对0到T一个周期进行积分，T时刻结束时的响应矩阵就是所求的状态转移矩阵Mo，求解其特征值的最大值即为该转速下的Floquet乘子，并由Floquet稳定性准则判定振动的稳定性。

旋转频率的计算范围为0～80 Hz，求得Floquet乘子如图13所示。

图13 Floquet乘子图Fig.13 Diagram of Floquet multiplier

由图13，在59～64 Hz的转频范围内Floquet乘子大于1，说明该范围内转轴受到周期性扭矩激励的振动是不稳定的，其余的旋转频率下是稳定的。本文采用的旋转频率为68 Hz，该旋转频率下的Floquet乘子小于1，因此在这个转速下进行激振是稳定的。

由Newmark法求得0～80 Hz旋转频率范围内每隔1Hz的轴心周期轨迹图和Poincaré图，分别如图14和图15所示。

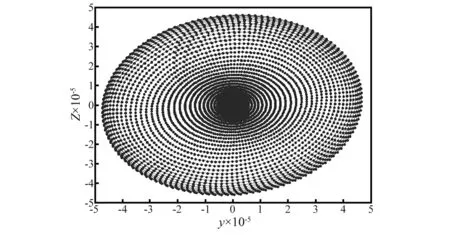
图14 节点P处轴心的周期轨迹Fig.14 Periodic orbit of pint P

图15 Poincaré映射截面Fig.15 Poincaré Section

图14的横坐标表示y方向的轴心位移周期轨迹，纵坐标表示z方向的轴心位移周期轨迹；图15的横坐标表示y方向的轴心位移周期轨迹，纵坐标表示y方向的轴心速度周期轨迹。每个旋转频率下的轴心周期轨迹和Poincaré映射截面都是封闭的圆环，系统做周期性运动[26]。由稳定性理论可知，转轴在大多数旋转频率下的弯扭耦合共振是周期稳定的。