高速动车电机架悬参数对转向架动力学性能影响研究

徐 坤， 曾 京， 黄彩虹， 祁亚运

(西南交通大学 牵引动力国家重点实验室，成都 610031)

目前，列车上牵引电机(以下简称电机)的悬挂方式主要分为三种：轴悬式、架悬式和体悬式[1]。在轴悬式中，电机大半质量成为簧下质量，增加了车辆对轨道的动力破坏作用，所以此悬挂方式主要用于低速车上。在国内外高速动车上普遍采用的是有利于降低动作用力的架悬式与体悬式，但由于体悬式结构复杂，制造及维护成本较高[2]，架悬式被越来越多地使用。在架悬式中，又分为刚性架悬和弹性架悬。刚性架悬是指电机与构架通过螺栓连接固结在一起的，弹性架悬是指电机通过吊板或者其它弹性原件悬挂在构架上，比如CRH3型动车组。电机弹性架悬是近年来高速机车和动车为了改善横向动力学性能采用的一种新技术[3-4]。

国内外学者对电机弹性架悬进行了广泛而深刻的研究：罗赟等[5]提出3个刚体的机车横向振动简单模型，结合轮对横向随机响应的特点，分析不同速度下，驱动装置悬挂参数对机车受迫振动的影响；马卫华等[6]对分别采用刚性架悬和弹性架悬方案时机车的横向稳定性、平稳性、轮轴横向力、轮重动态变化等进行了比较研究，研究结果表明，采用弹性架悬方案时机车各项直线高速运行指标均有所改善，且机车的动力学性能对悬挂参数的敏感性减弱。Huang等[7]根据电机架悬特点，推导出动车转向架动力学方程，分析了牵引电机架悬参数对转向架线性临界速度的影响；Alfi等[8]不仅分析了牵引电机架悬参数对整车线性临界速度的影响，还通过施加轨道不平顺来研究架悬参数对整车非线性临界速度的影响。以上文献都只是研究架悬参数对转向架或者整车动力学性能的影响，并未做出理论解释。姚远等[9-10]针对机车某B0转向架建立了10自由度单转向架横向动力学模型，从动力吸振角度对弹性悬挂做出了理论解释，但是并没有深入研究架悬参数对构架与电机相对横移的影响。

本文由简入繁，首先针对电机弹性架悬方式建立了等效到单轮对的2自由度横向简化模型，研究了在轮对横向激振下、在不同电机悬挂参数下，构架横移与轮对激励横移的关系和构架横移与电机横移的关系；然后针对CRH3型动车转向架电机悬挂方式，建立了8自由度电机弹性架悬单转向架横向动力学模型，比较了不同电机架悬参数对转向架动力响应的影响(包括理想光滑直线轨道和带有横向随机激扰直线轨道)；最后研究了电机架悬参数对转向架稳定性的影响。

1 电机弹性架悬横向简化模型

首先建立电机弹性架悬横向简化模型，简化模型选取等效到单轮对的横向运动系统，如图1所示，车体横向位置固定不动，轮对横向简谐激励作为系统的激励，考虑构架和电机的横移。

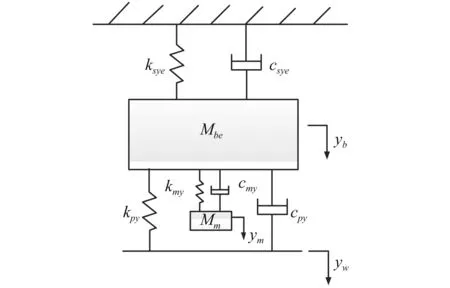
图1 电机弹性架悬横向简化模型Fig.1 A lateral simplified model of the elastic bogie-suspended motor

图1中，yb、ym分别代表构架、电机横向响应位移，yw代表轮对横向激励。ksye、csye分别为等效的二系横向刚度和阻尼，kpy、cpy分别为一系横向刚度和阻尼，kmy、cmy分别为电机悬挂刚度和阻尼，Mbe为等效的构架质量，Mm为电机质量。整个系统的运动微分方程为

(1)

(2)

首先来研究在轮对横向激振下，构架相对轮对的横移传递函数。对式(1)和式(2)Laplace变换后， 消去Ym后可得构架相对轮对横移传递函数G1(s)。

(3)

为了便于表达，在下面的论述中使用电机横移频率fmy和横移阻尼比ξmy， 来代替电机悬挂总的横移刚度kmy和总的横移阻尼cmy。kmy、cmy与fmy、ξmy的关系如下

kmy=(2πfmy)2Mm,cmy=2ξmyMm(2πfmy)

(4)

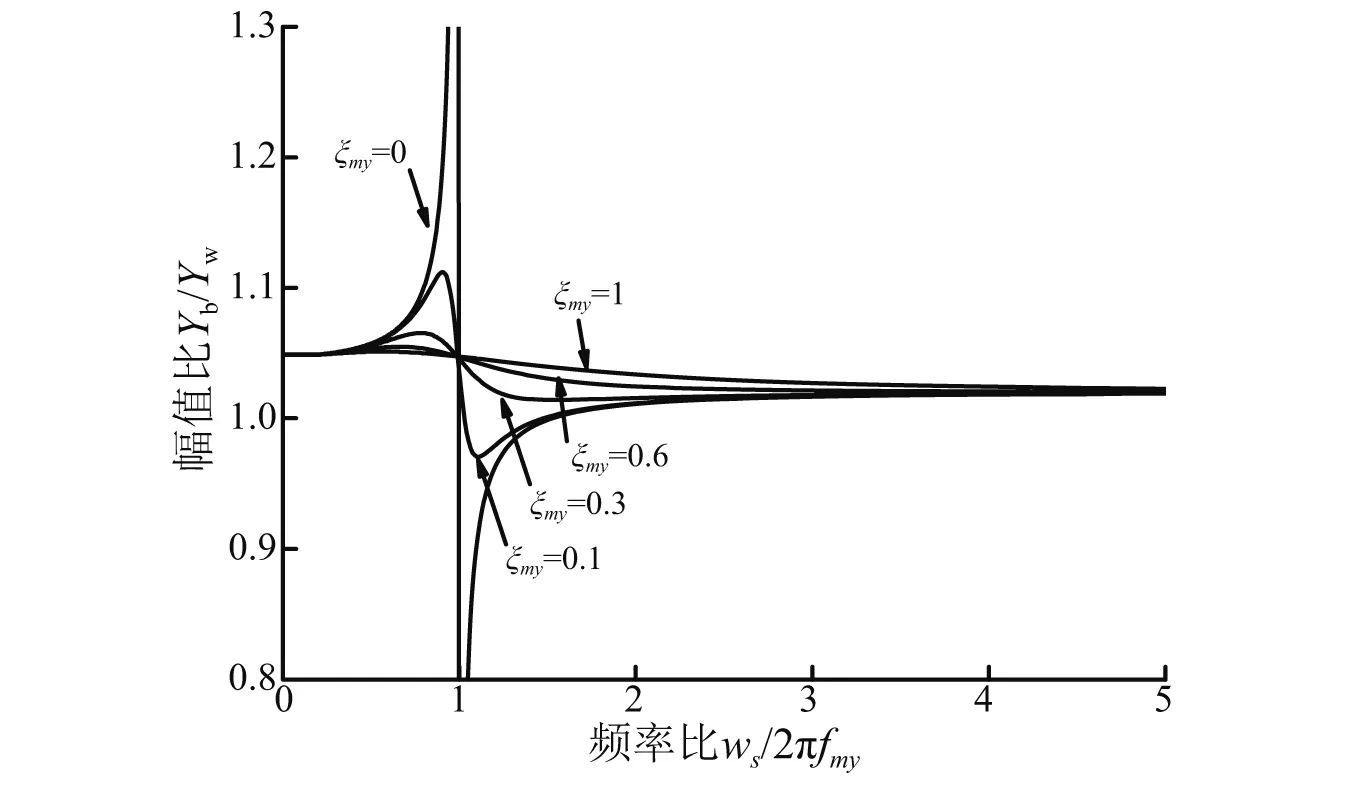
图2 不同下的构架与轮对幅值比Fig.2 The ratio of amplitude of frame to the wheel at different ξmy

接下来研究在轮对横向激振下，电机相对构架的横移传递函数。式(2)变Laplace换后，可得电机相对构架的横移传递函数G2(s)。

(5)

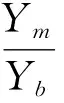
结合图2、式(5)可知， 当ξmy很小时， 如果fmy接近且略小于轮对横向激振频率时，构架振幅最小，但是此时电机相对构架的横移很大。电机作为重要的传动部件，不允许它有过大的运动。为了兼顾两者，在选择电机悬挂参数时，fmy要接近且略小于轮对横向激振频率， 但是ξmy要适当取大点。

2 电机弹性架悬转向架横向模型

对于CRH3型高速动车组，转向架的前后两台电机首先通过螺栓安装在专门设置的电机安装架上，使之成为一个整体，然后再借助位于该电机安装架四角的具有横向弹性的电机吊板安装在构架横梁的电机安装座上，如图3所示。这种独特的悬吊结构保证了在横向上由于吊板的弹性作用使得牵引电机能够在一定范围内横向弹性摆动，其横向质量与构架横向质量分离，提高了转向架的蛇行临界速度。

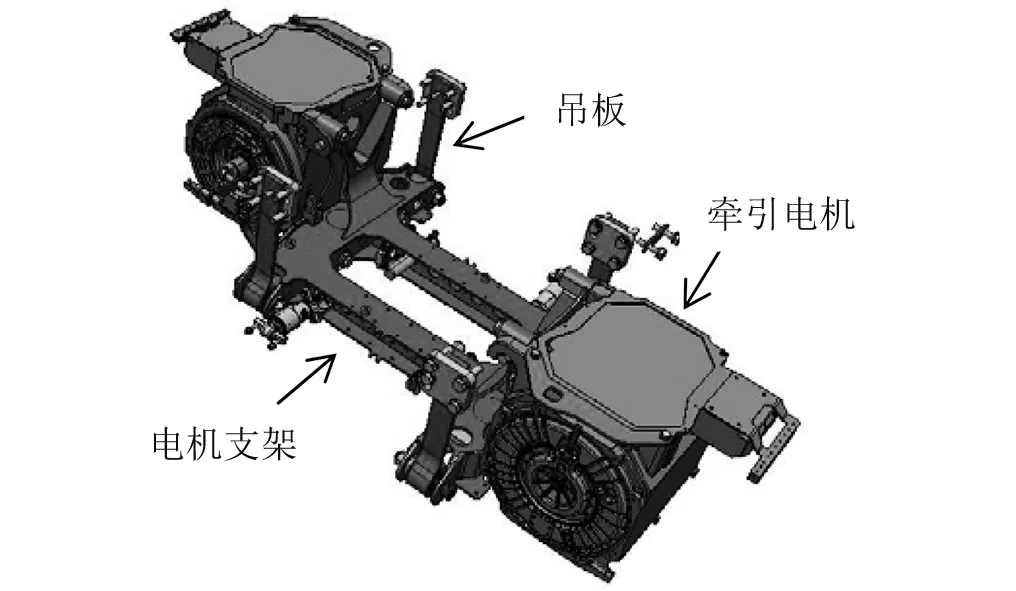
图3 CRH3型动车组牵引电机悬挂方式Fig.3 The type of traction motor suspension of CRH3

图4为CRH3型动车组电机弹性架悬单转向架横向模型，忽略车体运动的影响，车体仅仅作为一个参考系沿着轨道方向以恒定速度运行，假设构架与车体通过二系悬挂组件连接(不考虑抗蛇行减振器)。考虑轮对、构架和牵引电机的横向和摇头自由度。为了建模方便，做出如下假设：①一系和二系的悬挂特性都是线性的；②假设转向架构架质心高度与车轴中心线一致，由此可以忽略构架侧滚振动；③蠕滑力在线性区域工作，由此可以采用kaller线性蠕滑理论；④不考虑重力复原刚度和自旋蠕滑的影响。

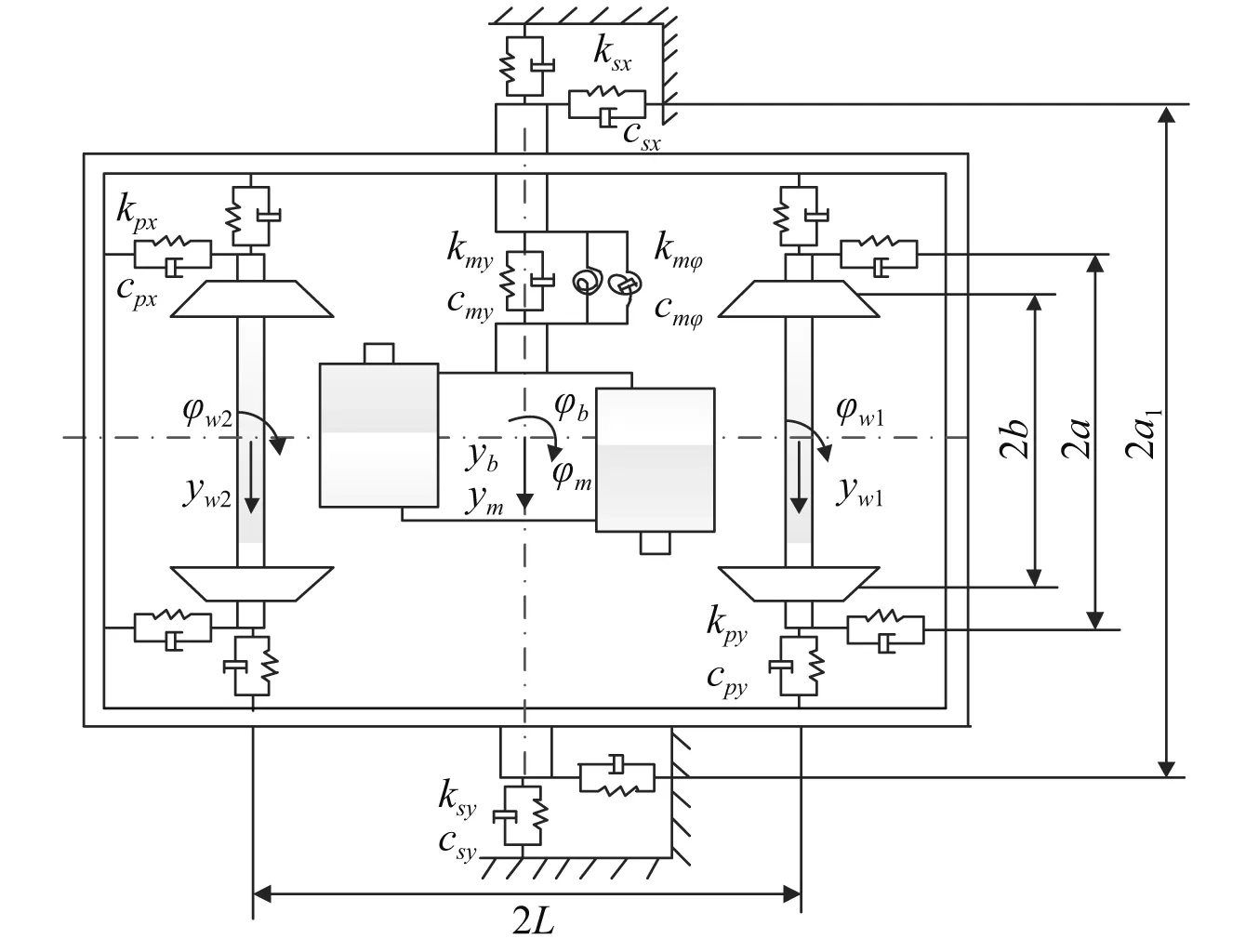
图4 电机弹性架悬转向架横向模型Fig.4 The lateral bogie model of elastic bogie-suspended motor

该模型有4个刚体，共8个自由度。其动力学方程为

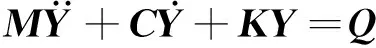
(6)

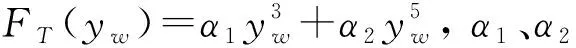
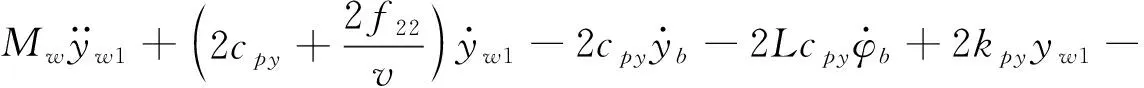
(7)

(8)

(9)

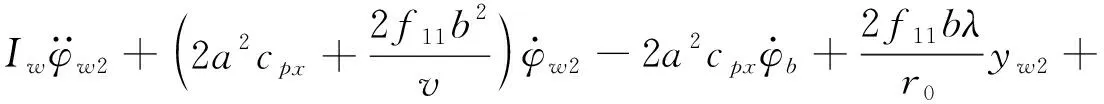
(10)

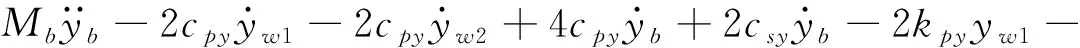
(11)

(12)

(13)

(14)

式(7)～式(14)参数意义及数值见附录。与用电机横移频率fmy和横移阻尼比ξmy来代替电机悬挂总的横移刚度kmy和总的横移阻尼cmy一样，使用电机摇头频率fmφ和摇头阻尼比ξmφ来代替电机悬挂总的摇头刚度kmφ和总的摇头阻尼cmφ。由于在实际中，电机摇头频率fmφ一般都很大，故本文只研究电机横移频率fmy及横移阻尼比ξmy比对转向架动力学性能的影响。

3 电机架悬参数对转向架动力响应的影响

在转向架横向模型中，轮对的蛇行频率是作为整个系统的激振频率，因此首先求出在不同电机悬挂频率下，转向架的蛇行频率。求出在不同速度下，不同悬挂频率下，整个系统的特征根，提取出蛇行模态频率。表1为不同速度下，不同悬挂频率下的蛇行频率。

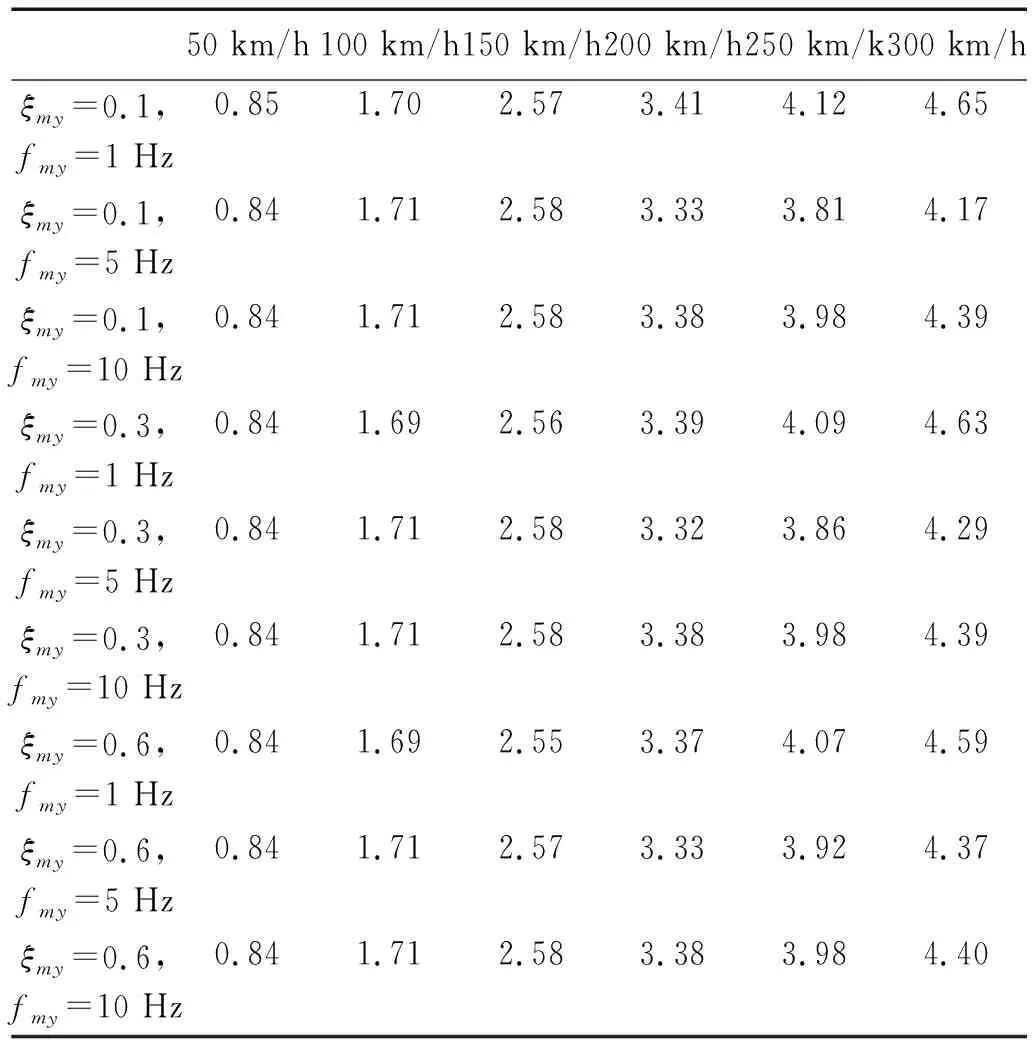
表1 不同速度下，不同悬挂频率下的蛇行频率Tab.1 The frequency of huntingat different speeds and different suspension frequencies Hz

从表1可以看出，随着运行速度v的增大，蛇行频率随之增大。当v≤200 km/h时，不同悬挂频率下的蛇行频率相差很小，最大相差2.6%，而当运行速度v≥250 km/h时，不同悬挂频率下的蛇行频率相差稍稍有所增大，最大相差10.3%。

3.1 理想光滑直线轨道

在理想光滑轨道上，系统只承受轮对的简谐蛇行激励。为了便于计算结果的对比，ξmy适当取小一点，v适当取大一点。 图5为当ξmy=0.1、v=300 km/h时，fmy在1～10 Hz之间，构架横向位移幅值和电机相对构架横向位移幅值的变化趋势。

由图5可以看出，当fmy=4 Hz时，构架横向位移幅值最小，而当fmy=4.5 Hz时，电机相对构架横向位移幅值最大，而此时转向架蛇行(即轮对蛇行)频率大约为4.2 Hz左右。所以可以得到： 当fmy接近且略小于转向架蛇行频率时，构架横向位移幅值最小，但此时电机相对构架横向位移幅值很大。这与第一小节的结论是一致的。

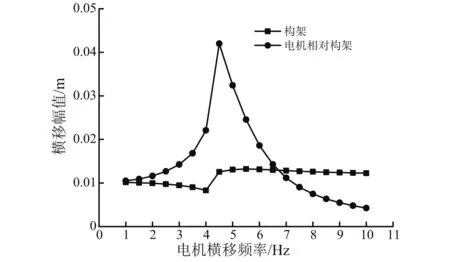
图5 fmy对构架横移幅值、电机相对构架横移幅值的影响Fig.5 The influence of fmy on the lateral displacement amplitude of the frame and the rotor relative to the frame

为了形象地说明构架、电机相对构架横移关系，画出当fmy为1 Hz、4 Hz和10 Hz，得到构架横移及电机相对构架横移时域图6。

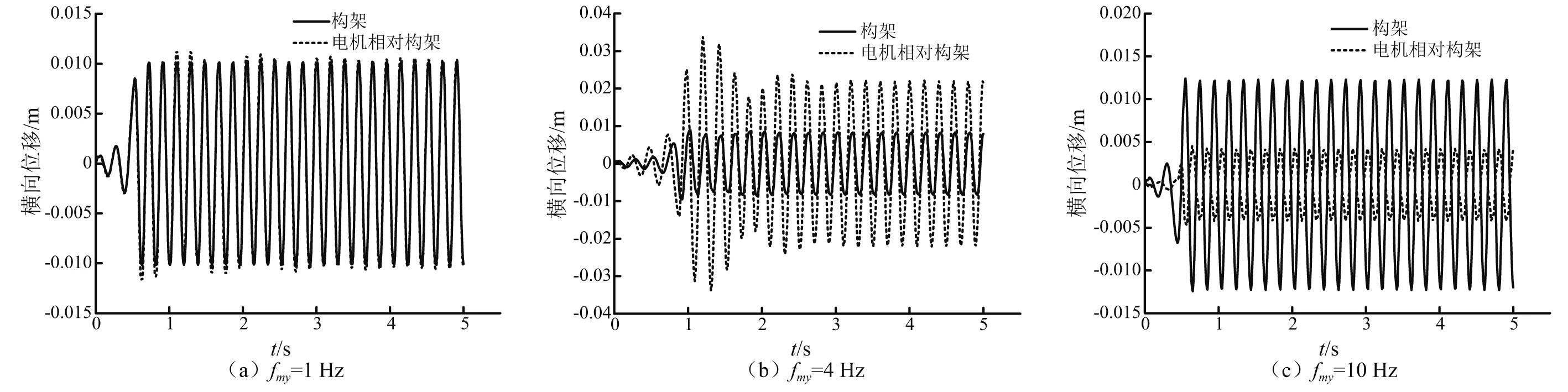
图6 不同fmy下构架、电机相对构架横移时域图Fig.6 The time domain diagram of lateral displacement of frame and motor to frame

从图6可以看出， 当fmy=1 Hz时，构架横移幅值、电机相对构架横移幅值几乎是相等的； 当fmy=4 Hz时， 构架横移幅值小于电机相对构架横移幅值； 当fmy=10 Hz时，构架横移幅值大于电机相对构架横移幅值。以上规律与图5是一致的。

3.2 具有横向随机不平顺激扰直线轨道

当车辆在理想直线轨道上以低于蛇行运动临界速度运行时，产生的自激振动时逐渐衰减的，但车辆在实际轨道运行时，轮对、转向架和车体都要产生持续的横向振动，这种振动是由横向随机不平顺激扰引起的，具有强迫振动的性质[12]。当在具有方向不平顺激扰ya(t)时，式(7)、式(9)轮缘力分别为

(15)

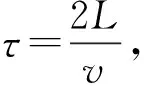
图7为一段实测轨道方向不平顺激扰。

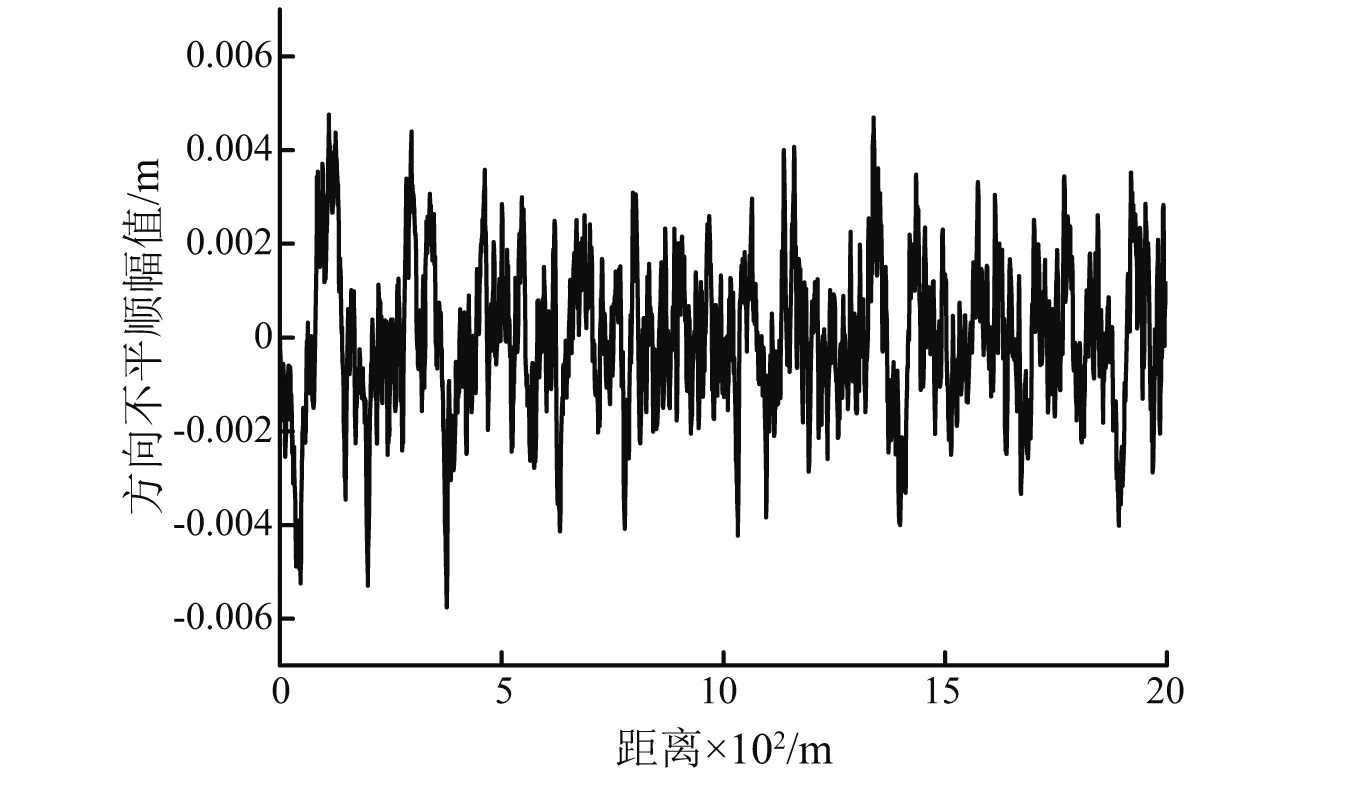
图7 轨道方向不平顺激扰Fig.7 The irregular disturbance of direction of the track

图8为当v=300 km/h，ξmy=0.1时， 构架横移均方根、构架与电机相对横移均方根随fmy变化而变化趋势图。

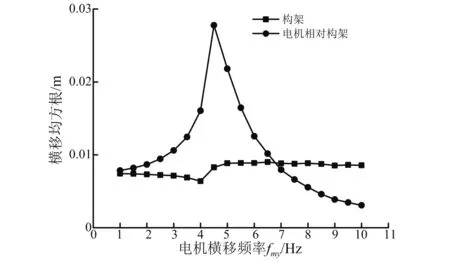
图8 fmy对构架横移均方根值、电机相对构架横移均方根值的影响Fig.8 The influence of fmy on the lateral displacemen rms of the frame and the rotor relative to the frame

从图8可以看出，在有横向随机不平顺直线轨道，fmy对构架横移均方根值、电机相对构架横移均方根值的影响与理想光滑直线轨道fmy对构架横移幅值、电机相对构架横移幅值的影响规律是一致的。

4 电机架悬参数对转向架稳定性的影响

研究架悬参数对转向架动力学性能影响主要是研究其对转向架稳定性的影响。对线性系统方程(7)～(14)用状态空间表示，共16阶。再求这16阶系统矩阵的特征值与特征向量，得到8对共轭特征值与特征向量。每一对特征根具有如下形式

γn=αn±βni,n=1,2,…,8

(16)

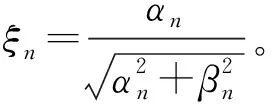
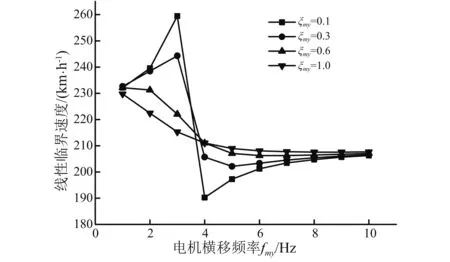
图9 fmy、ξmy对转向架线性临界速度的影响Fig.9 The influence of fmy and ξmy on linear critical speed of bogie

从图9中可以看出，ξmy越小， 线性临界速度越大，且最优fmy(线性临界速度最大时的fmy)均接近但略小于各自的蛇行频率。结合前面的论述，当取最优fmy时，此时构架的振幅最小，但电机相对构架振幅很大，电机在此时相当于一个动力吸振器，把构架的振动转移到电机上来。

根轨迹曲线是线性系统方程在不同速度下的特征根计算结果， 当ξmy=0.3时， 最优fmy=3 Hz， 做出fmy=1 Hz、3 Hz、10 Hz时，速度在5～300 km/h(间隔5 km/h)转向架蛇行运动的根轨迹,如图10所示。

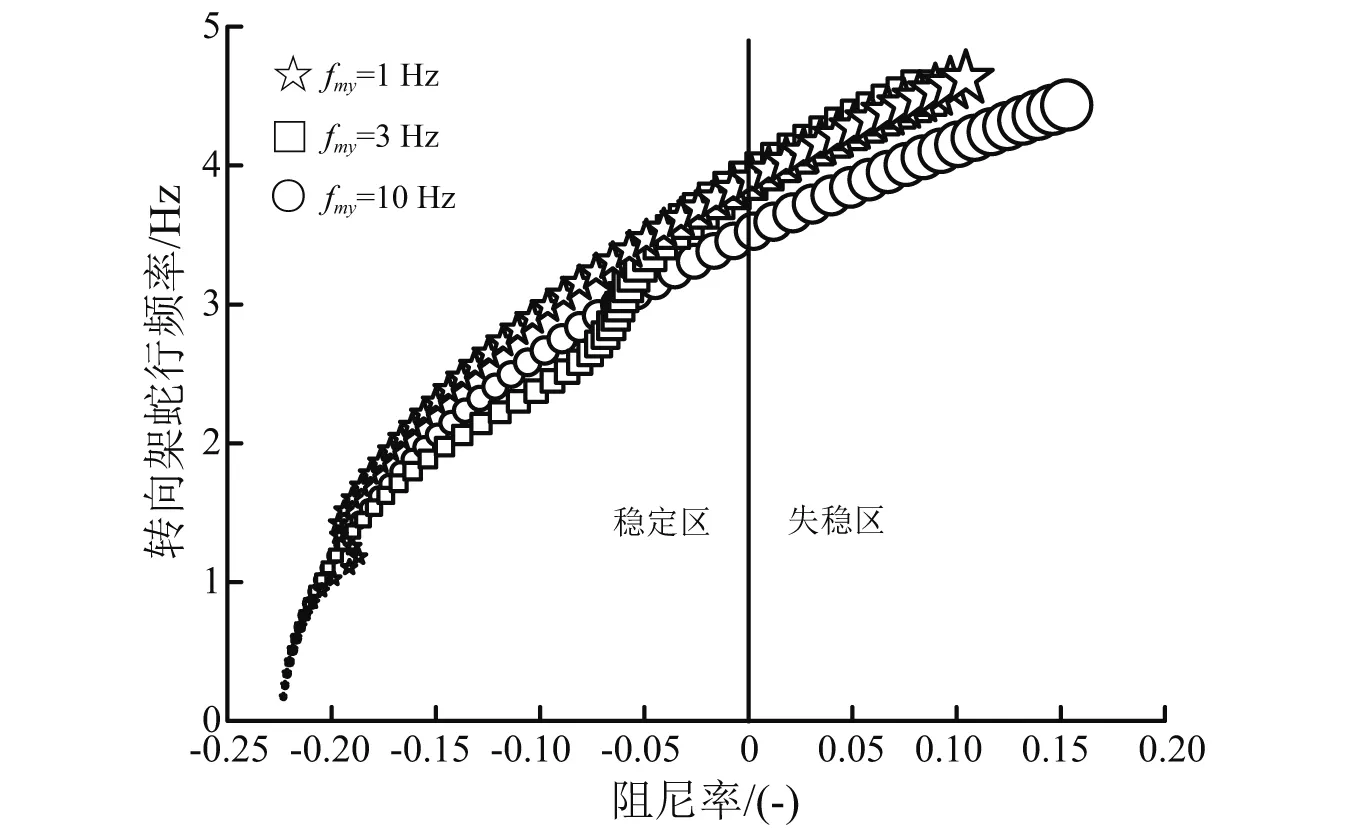
图10 不同fmy转向架根轨迹图Fig.10 Root loci curves of bogie for different values of fmy

在图10中，图形尺寸越大，代表速度越大。低速时，转向架蛇行运动阻尼率小于0，是稳定的，随着速度越来越大，转向架蛇行频率越来越大，阻尼率越来越接近0，当大于0时，系统失稳。当fmy=1 Hz时， 根轨迹在阻尼率为-0.2时发生扭曲， 当fmy=3 Hz时，根轨迹在阻尼率为-0.07时发生扭曲，fmy=10 Hz时，根轨迹几乎不发生扭曲。由此看见根轨迹扭曲发生在阻尼率为0的附近，临界速度会发生剧烈变化。

5 结 论

(1) 在低速下，电机横移频率及横移阻尼比对转向架蛇行频率的影响很小，在高速时，这种影响会稍微变大。

(2) 在理想光滑直线轨道和具有横向随机不平顺激扰的直线轨道上，当电机横移频率接近且略小于转向架蛇行频率时，构架横移最小，电机相对构架横移很大。而且横移阻尼比越小，构架横移越小，电机相对构架横移越大。

(3) 当电机横移频率接近且略小于转向架蛇行频率时，转向架线性临界速度最大，且横移阻尼比越小，线性临界速度越大，但是电机相对构架横移也越大。电机作为重要的传动部件，不允许它有过大的运动。为了兼顾两者，可以把横移阻尼比适当取大一点。

(4) 当构架横移很小而电机相对构架横移很大时，电机相当于一个动力吸振器，把构架的振动转移到电机上来，使电机悬挂阻尼耗散能很大，增强了转向架的稳定性，进而提高了转向架的线性临界速度。