基于广义复合多尺度排列熵与PCA的滚动轴承故障诊断方法
2018-11-01郑近德刘庆运
郑近德, 刘 涛, 孟 瑞, 刘庆运
(安徽工业大学 机械工程学院,安徽 马鞍山 243032)
由于机械系统的复杂性,设备在运转的过程中不可避免地会出现摩擦、振动、负载和冲击等,振动信号往往表现为一定的非线性和非平稳性。许多非线性分析的方法,如分形,近似熵,样本熵,排列熵和多尺度排列熵等因能够提取隐藏在振动信号中线性分析方法无法提取的非线性故障特征而在故障诊断中得到了越来越多的应用[1]。如石博强等[2]研究了旋转机械故障信号的的分形特征;胥永刚等[3-4]将近似熵应用于机械故障诊断,将其与分形维数进行了对比;Yan等[5]将排列熵应用于机械系统的振动信号的特征提取和状态监测,结果表明排列熵能够有效地检测滚动轴承振动信号的动态变化和表征不同状态下的工况特征;郑近德等[6-7]提出一种自适应多尺度排列熵的滚动轴承故障诊断方法,并将多尺度排列熵(Multiscale Permutation Entropy, MPE)应用于滚动轴承故障特征提取与诊断等。
然而,研究发现,MPE还存在如下缺陷:①基于粗粒化方式定义的多尺度计算方法依赖于时间序列的长度。由于每个粗粒化序列的长度等于原信号长度除以尺度因子,因此,熵值的偏差会随着粗粒化序列长度减小而增大[8];②粗粒化过程将一个时间序列分割为等长的非重叠的片段再计算每一个片段内所有数据点的均值。只采用了数据的均值这单一特征得到原始信号不同尺度的序列,不可避免地会造成许多潜在有用信息的丢失[9]。对此,本文采用复合多尺度的方法以克服传统粗粒化方式的不足,同时将粗粒化过程中一阶矩(均值)推广到二阶矩(方差),实现时间序列的粗粒化,由此得到了广义复合多尺度排列熵(Generalized Composite Multiscale Permutation Entropy,GCMPE)。
正常滚动轴承振动是随机振动,当滚动轴承发生故障时,振动信号的随机性和动力学行为发生改变。由于背景噪声及机械系统的复杂性,振动信号中与故障有关的特征信息往往分布在不同的时间尺度,振动信号的随机性和动力学行为改变也发生在不同尺度。因此,对振动信号进行GCMPE分析能够有效的提取滚动轴承故障特征。在提取滚动轴承的振动信号的GCMPE后,采用主元分析(Principal Component Analysis,PCA)降低特征值维数[10]。为了实现故障诊断智能化,将适合小样本分类的支持向量机(Support Vector Machine,SVM)用于故障模式的自动识别[11-12],提出了一种基于GCMPE,PCA与SVM的滚动轴承故障诊断方法。将提出的方法应用于实验数据分析,结果表明了论文方法的有效性和优越性。
1 多尺度排列熵算法
1.1 排列熵算法
考虑时间序列{x(i),i=1, 2, …,N},对其进行相空间重构,得到:X(1),X(2), …,X(N-(m-1)λ);这里X(i)={x(i),x(i+λ), …,x(i+(m-1)λ)},i=1,2,…,N-(m-1)λ,m是嵌入维数,λ是时间延迟。
将X(i)中的m个元素按照升序重新排列:
X(i)={x(i+(j1-1)λ)≤x(i+(j2-1)λ)≤…≤x(i+(jm-1)λ)};
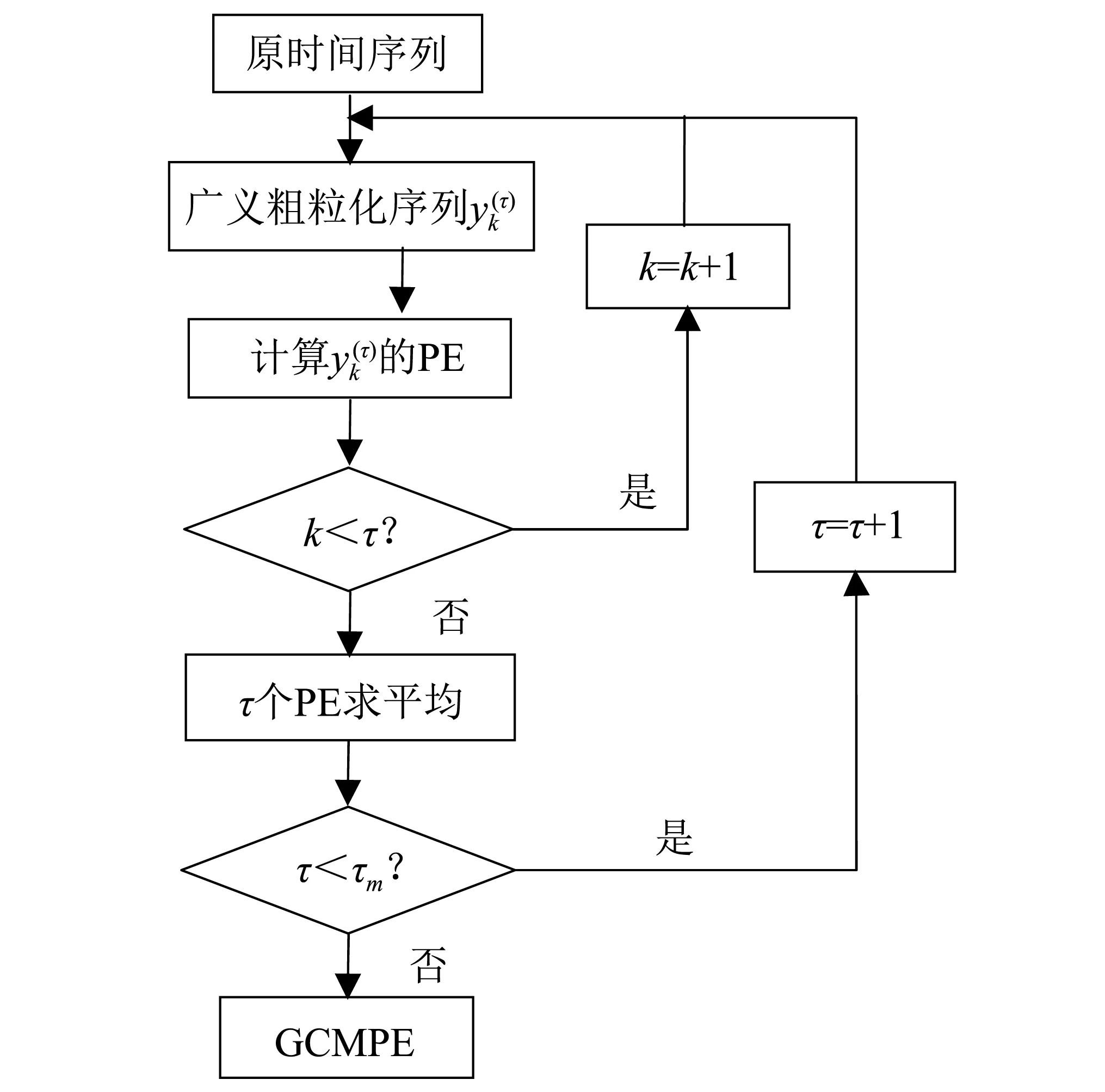
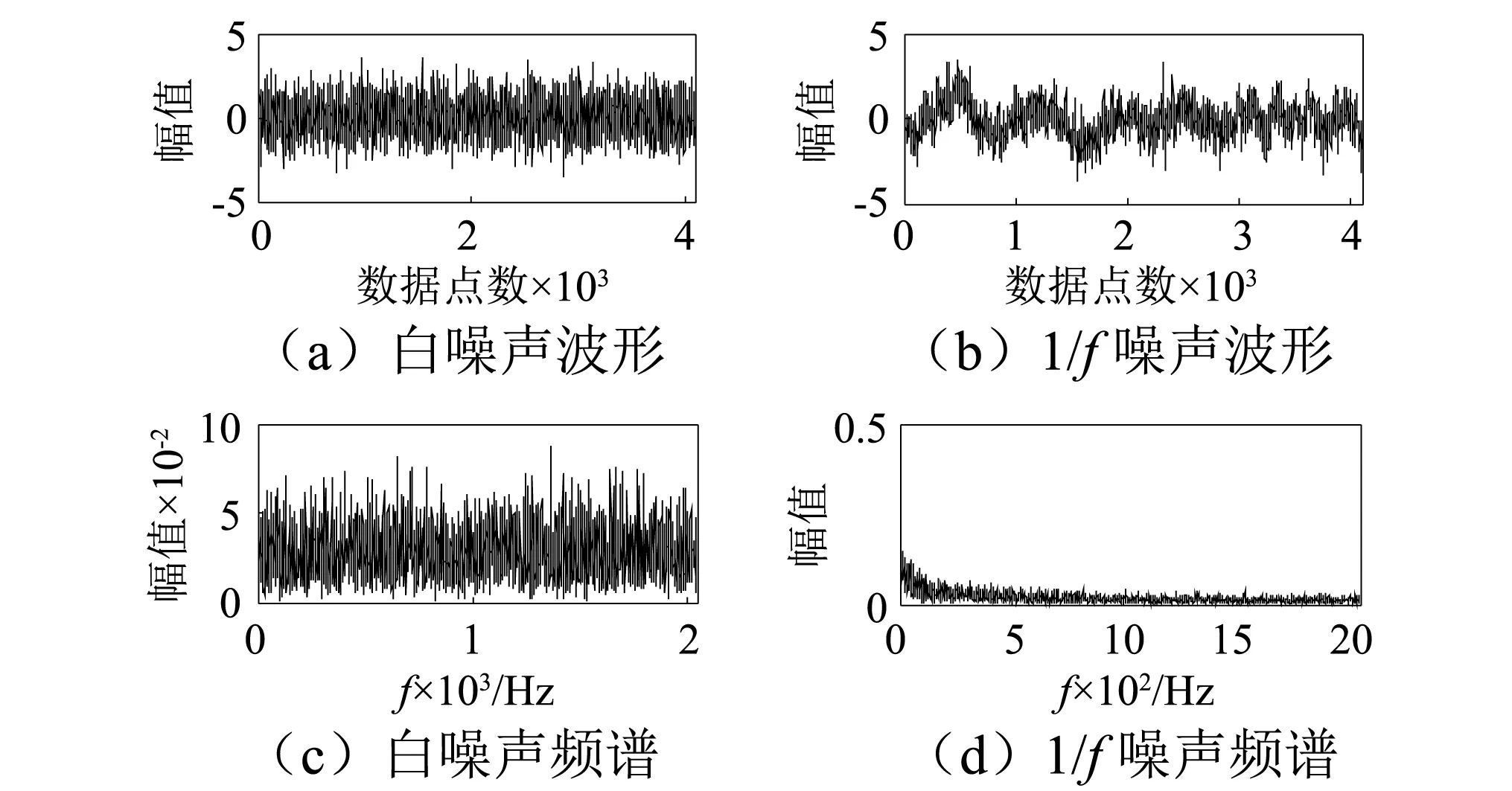
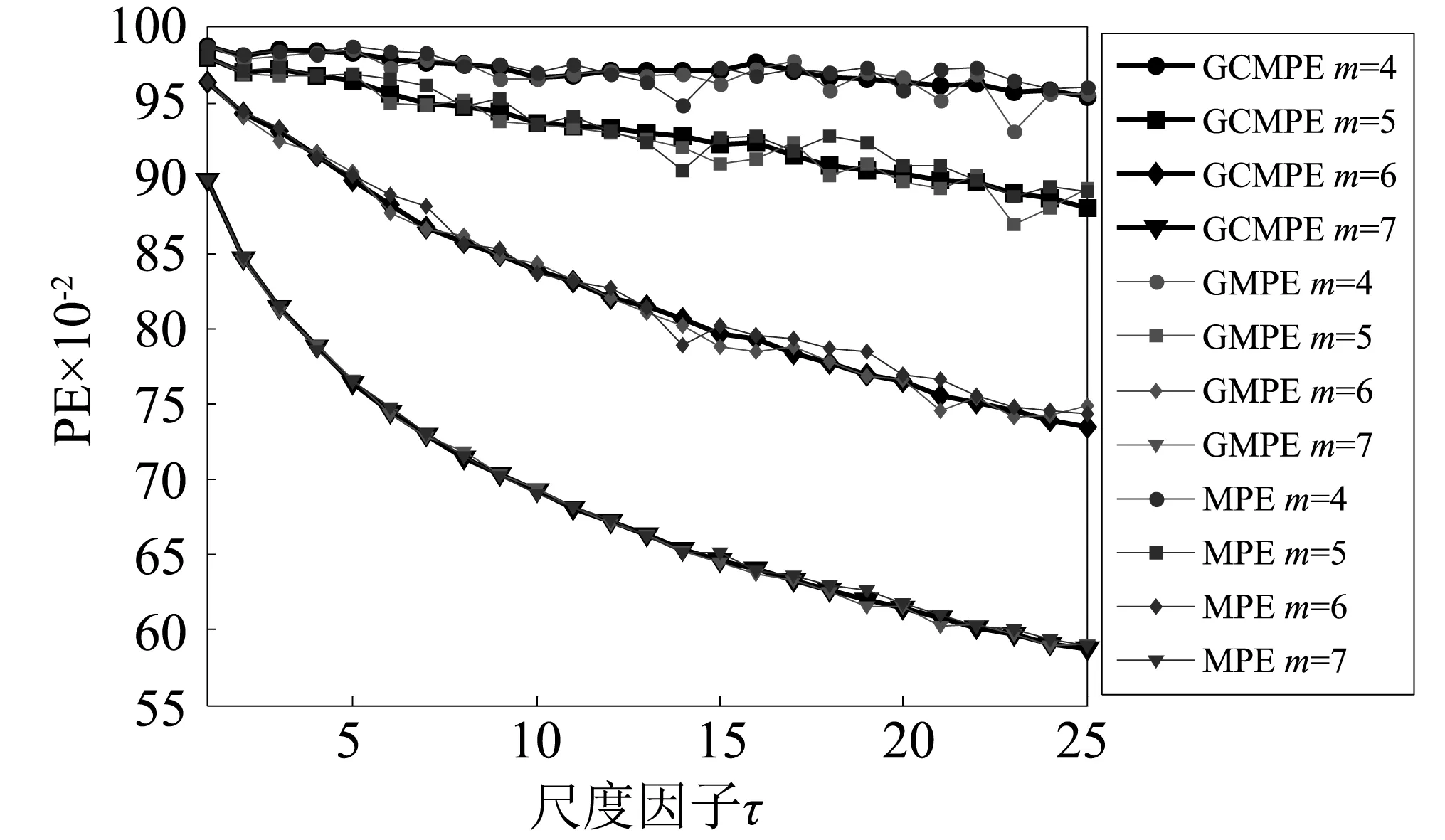
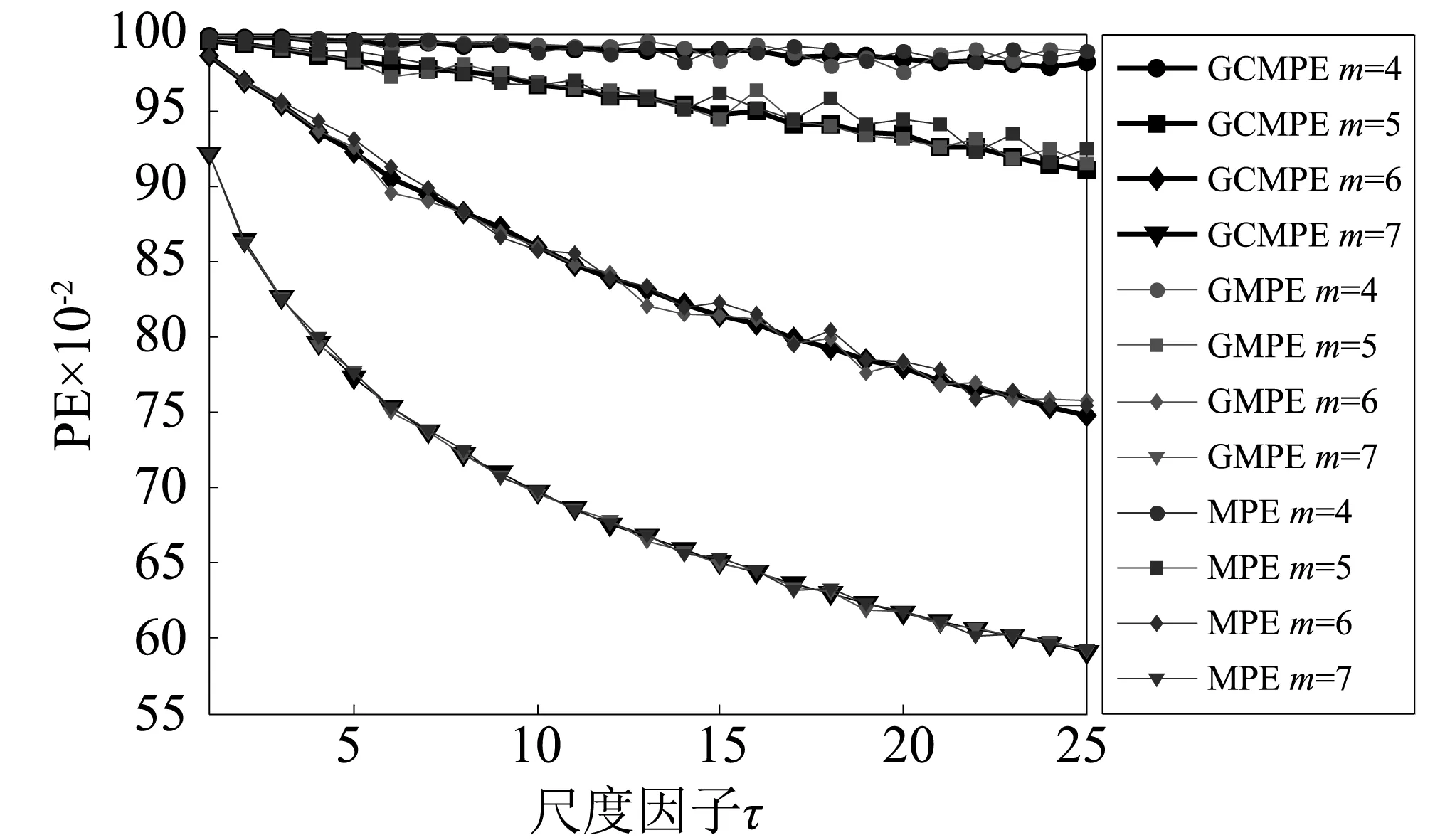
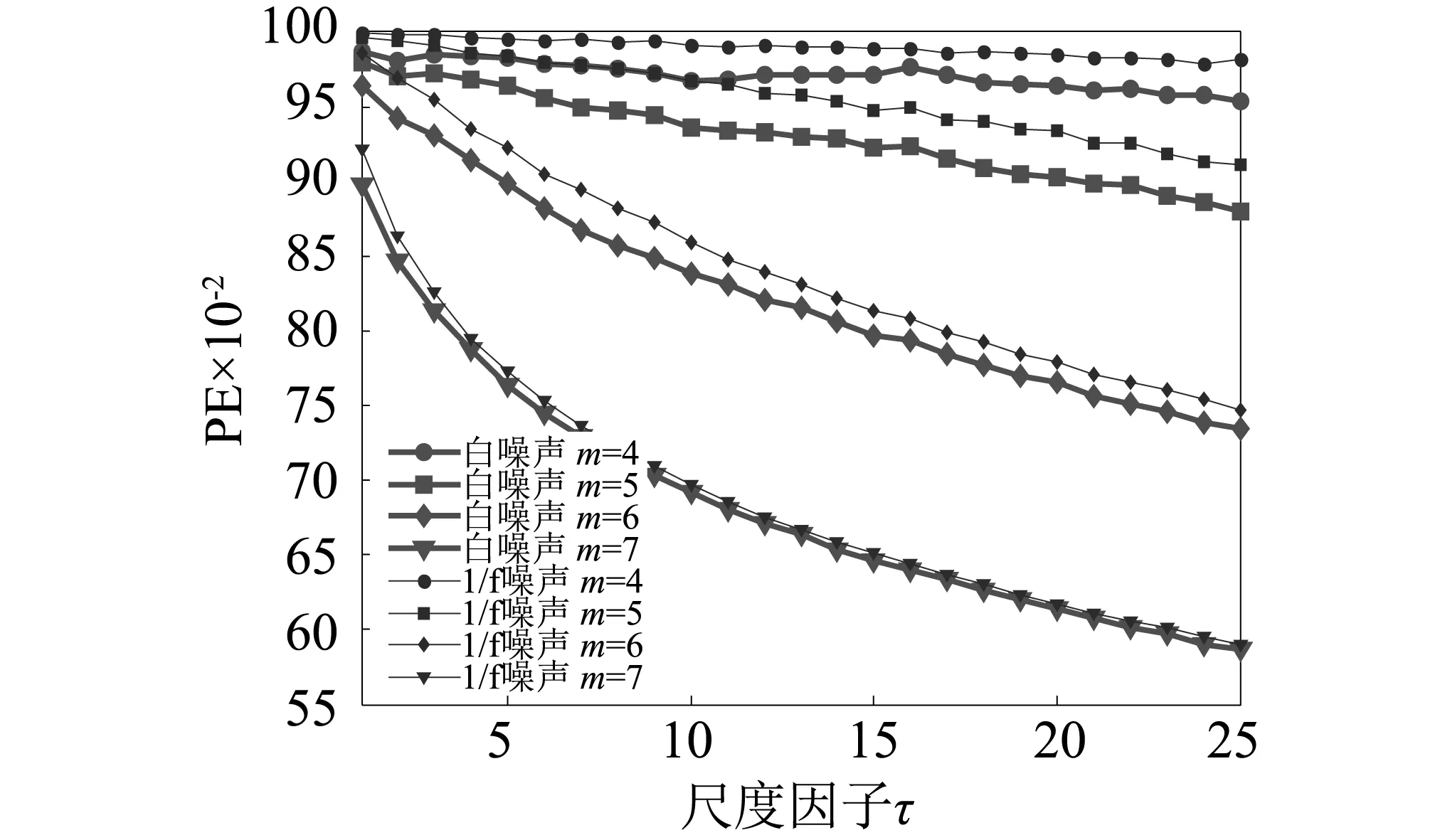
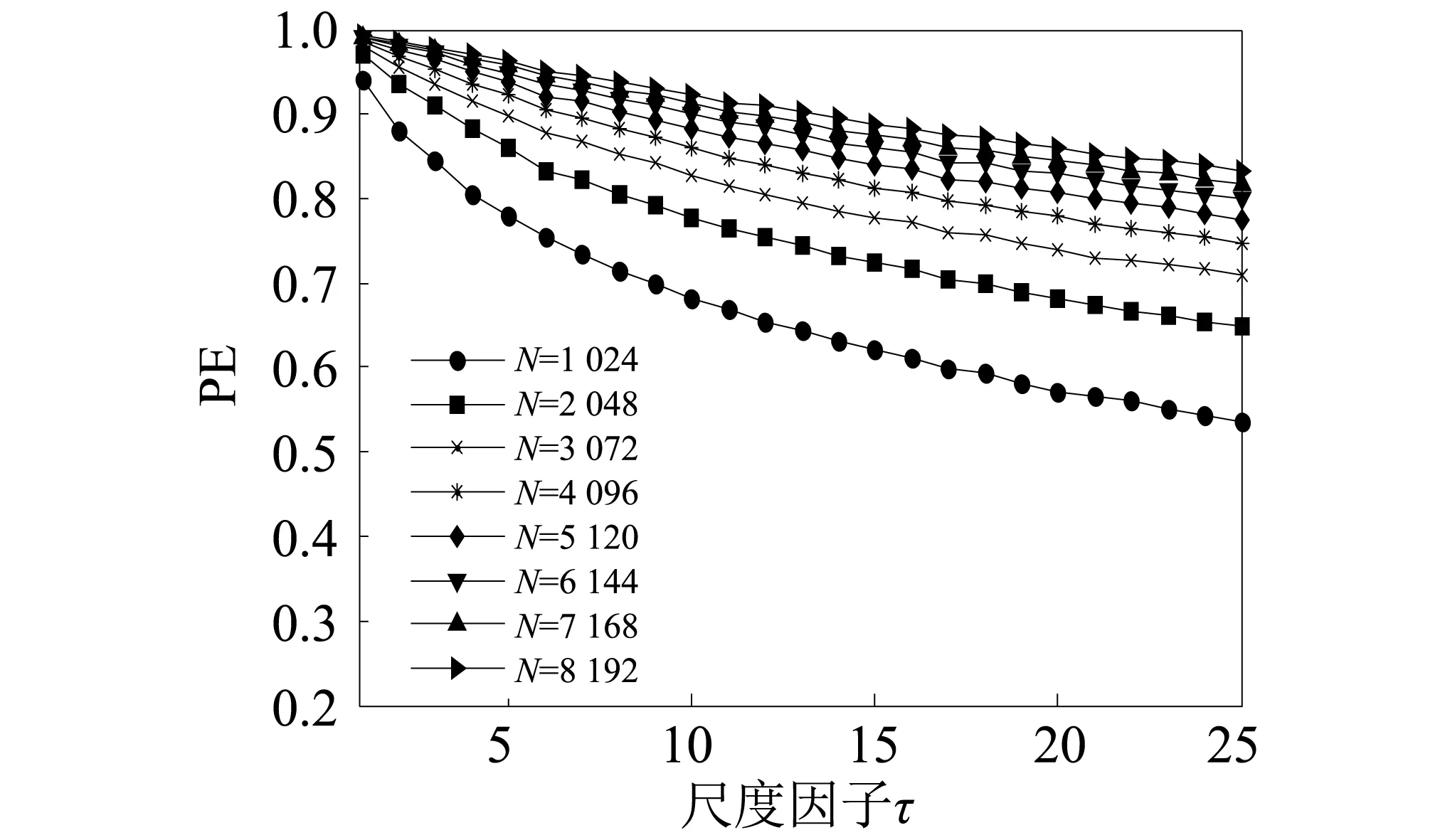
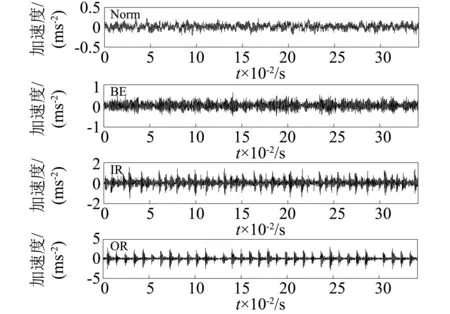
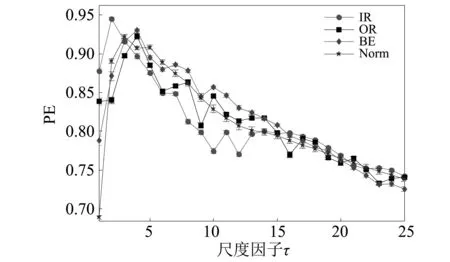
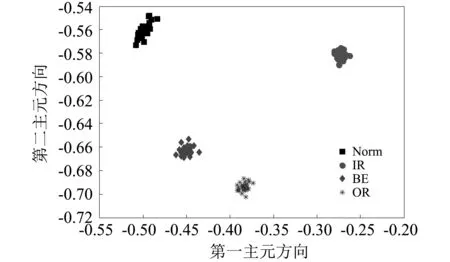
若有:x(i+(ji1-1)λ)=x(i+(ji2-1)λ),则按j值的大小进行排序,即当jk1 (1) 注意到当Pg=1/m!时,Hp(m)达到最大值ln(m!),通过ln(m!)将Hp(m)归一化 Hp=Hp(m)/ln(m!) (2) Hp的取值范围是0≤Hp≤1。Hp值的大小表示时间序列的复杂和随机程度。Hp越大,说明时间序列越随机,反之,则说明时间序列越规则。 PE只能分析时间序列单一尺度的随机性和动力学突变行为,为了分析时间序列在不同尺度下的随机性和动力学突变行为,有学者提出了多尺度排列熵(MPE),计算步骤如下[13]。 (3) 式中:τ为尺度因子。τ=1时粗粒化序列即为原时间序列;τ>1时原始序列被分割成长度为[N/τ]([·]表示取整)的粗粒化序列。 (2) 计算每个粗粒化序列的PE,即 MPE(X,τ,m,λ)=PE(y(τ),m,λ) (4) GCMPE的计算步骤如下: (5) (3) 再将τ个PE值的均值视为原时间序列在尺度因子τ的PE值,即 (6) 式(6)得到的PE值画成尺度因子的函数,称为复合多尺度排列熵分析(GCMPE)。MPE算法中粗粒化序列都只考虑了一种粗粒化方式,不可避免地会遗漏很多重要信息。GCMPE不仅综合了同一尺度下多个粗粒化序列的信息,且将一阶矩推广到二阶矩(方差),理论上GCMPE要优于MPE方法。GCMPE与MPE类似,都是衡量时间序列随机性和检测动力学突变行为的方法,与单一尺度的PE不同,GCMPE和MPE从多个尺度对时间序列进行分析。如果一个时间序列的GCMPE(或MPE)在大部分尺度上比另一个时间序列PE值大,这说明前者比后者的随机性更强,发生动力学突变行为的概率更高。 最后,GCMPE的取值与嵌入维数m,时间延迟λ和尺度因子τ的选择有关。m太小重构的向量中包含太少的状态,算法失去意义和有效性,不能准确检测时间序列的动力学突变;但是m过大相空间的重构将会均匀化时间序列,此时不仅计算耗时,而且也无法反映序列的细微变化,因此,嵌入维数m一般取值4~7[14]。时间延迟λ对PE计算的影响较小,一般λ=1。尺度因子τ的最大值τm的选取没有一定的标准,一般选择τm≥10。GCMPE的计算流程,如图1所示。 为了研究参数对GCMPE分析结果的影响,不失一般性,考虑随机信号白噪声和1/f噪声。与白噪声相比,1/f噪声功率谱更为复杂,包含了更多模式信息。因此,在大部分尺度上1/f噪声的PE应比白噪声大。为了对比,将MPE中粗粒化方式采用广义粗粒化而未采用复合平均的方式得到的MPE方法,称为广义多尺度排列熵(Generalized Multiscale Permutation Entropy,GMPE)。即在GCMPE的计算步骤(2)中,对于尺度因子τ,只计算广义粗粒化序列中k=1的粗粒化序列的PE值,并将其作为时间序列在该尺度因子下的PE值。 为了研究嵌入维数m对计算结果的影响,以数据点数为4 096的白噪声和1/f噪声为例,二者的波形及频谱如图2所示。依据文献[14],在m=4, 5, 6, 7的条件下,分别采用MPE,GMPE和GCMPE对两种噪声进行分析,结果分别如图3和图4所示,其中时间延迟λ=1,最大尺度因子τm=25。 图1 GCMPE的计算流程图Fig.1 The flowchart of GCMPE 由图3和图4可以得出,首先,在相同的嵌入维数的情况下,白噪声和1/f噪声的MPE,GMPE和GCMPE值比较接近;但随着尺度因子的增大,MPE和GMPE的PE值波动和偏差增大,而GCMPE则变化趋势比较平缓,波动较小,对比结果体现了GCMPE的优越性。其次,嵌入维数m较小时(4和5),PE值的变化不明显,无法体现进行多尺度分析的优势。而m较大时,重构过程将会均匀化时间序列,无法反映序列的细微变化,m越大越无法区别结构相近的时间序列。且由图5白噪声和1/f噪声的GCMPE对比,可以看出,m=7时GCMPE无法区分白噪声和1/f噪声。因此,一般取m=6。 图2 白噪声与1/f噪声波形及频谱Fig.2 Waveforms and spectrum of white noise and 1/f noise 图3 不同嵌入维数下1/f噪声的MPE,GMPE和GMPE对比Fig.3 MPE, GMPE and GCMPE of 1/f noise under different embedding dimensions 图4 白噪声在不同嵌入维数下的MPE,GMPE和GMPE对比Fig.4 MPE, GMPE and GCMPE of white noise under different embedding dimensions 为了研究数据长度对GCMPE分析结果的影响,分别计算长度N为1 024,2 048, 3 072,4 096,5 120,6 144,7 168和8 192的白噪声信号,结果如图5所示,其中m=6,λ=1。由图6可以发现,当尺度因子小于等于10时,长度大于等于3 072的白噪声的PE值的相对误差在10%以下,最短粗粒化序列的长度约为300。当尺度因子等于20时,长度大于等于4 096的白噪声的PE值的相对误差在10%以下,此时粗粒化序列的长度约为200。为了减少误差,时间序列的长度应满足N≥200τm。最后,一般λ对GCMPE的影响很小。综上,选择嵌入维数m=6,λ=1,时间序列长度N≥200τm。 图5 不同嵌入维数计算的白噪声和1/f噪声GCMPE对比Fig.5 GCMPEs of white and 1/f noises estimated under different embedding dimensions 图6 白噪声在不同数据长度下的GCMPE对比Fig.6 GCMPE of white noise under different lengths 论文将GCMPE应用于滚动轴承故障振动信号故障特征的提取,提出了一种基于GCMPE,PCA与SVM的滚动轴承故障诊断方法,步骤如下: (1) 假设滚动轴承包含K类状态,每一类样本数目分别为M1,M2, …,MK;计算每一类每一个样本振动信号的GCMPE,得到K个故障特征集。 (2) 采用PCA对K个故障特征集进行降维处理,前q(q<τm)个主元作为原始特征集的敏感故障特征。 (3) 将K个故障特征集的每一个故障特征子集分为2Mk/3个训练样本和Mk/3测试样本,k=1, 2, …,K。 (4) 将训练样本输入到基于SVM的K类故障分类器,对其进行训练。其中基于SVM的K类故障分类器采用偏二叉树建立。 (5) 采用测试样本对多故障分类器进行测试,依据分类器输出结果判断滚动轴承的状态。 试验数据采用美国Case Western Reserve University的滚动轴承试验数据。测试轴承为6205-2RS深沟球轴承,采用电火花技术在轴承上布置单点故障,故障直径为0.533 4 mm,深度为0.279 4 mm,主轴转速为1 730 r/min,采样频率为12 kHz,采集到滚动体故障(Ball element,BE)、正常(Norm)、外圈故障(Outer Race,OR)和内圈故障(Inner Race fault,IR)四种状态轴承的振动加速度信号,每种状态取29组数据样本,每个样本点数为4 096,四种振动信号的波形,如图7所示。 上述四种滚动轴承故障类型的数据,每种状态取29个样本,共116个样本。计算每一个样本的GCMPE,每种状态所有29个数据样本的均值和标准差如图8所示。由图中可以看出,每一类样本的标准差非常小,即单个样本的GCMPE偏离均值较小,这说明GCMPE的计算较稳定。在尺度因子等于1时,正常滚动轴承的PE值较小,小于其它三类故障轴承振动信号的PE值;由此可见,PE适合滚动轴承的故障检测。此种情况下,若要区分正常与故障轴承,取PE阈值0.75即能够有效的检测轴承是否发生故障。但是仔细观察发现,单一尺度PE虽然能够检测有无故障,若要进一步识别故障位置则需要更多的信息。从图8中也易发现,四种状态轴承振动信号在不同的尺度因子下的PE值明显不同。当考虑单一尺度的PE时,四者的大小关系是:PEIR>PEOR>PEB>PENorm;但考虑多尺度时,这种关系不再成立。例如当4≤τ≤16时,PEB>PENorm>PEOR>PEIR;这说明单一尺度的PE值并不能完整地反映故障的全部信息,其它多个尺度也包含重要故障特征信息。当17≤τ≤25时,四种状态振动信号的GCMPE非常接近,区别不大,与实际相符。综上,GCMPE能够有效地反映滚动轴承振动信号的故障特征。 图7 滚动轴承振动信号时域波形Fig.7 Waveforms of vibration signal of rolling bearing 图8 滚动轴承四种状态振动信号的GCMPEFig.8 GCMPEs of vibration signals of rolling bearing under four different states 采用PCA对得到的GCMPE特征值进行特征降维,输出结果如图9所示,其中PCA降维子空间维数为5。由图中可以看出,不同状态的各类数据都能够区分得较为明显,正常样本和各类故障样本区分比较明显,而且每一类的各个样本的特征相对比较集中。最后,从每一类状态样本集中随机选择19个样本,每一类剩余的10个样本作为测试样本。将每一类样本降维后的前两个主元特征作为敏感故障特征输入到基于SVM的多故障分类器进行训练,SVM程序参见文献[15],参数采用默认设置。将测试样本输入到已训练好的分类器进行测试,40个测试样本都得到了正确分类,故障识别率为100%,这说明了论文方法的有效性。 为了对比,计算所有样本MPE,再采用PCA进行降维处理,对得到的故障特征输入到基于SVM的多故障分类器。经过同样的训练过程,测试样本的输入结果也为100%。这说明MPE也能够有效的提取滚动轴承的故障特征信息。但在分类之前,将PCA降维处理的结果输出,如图10所示。由图中可以看出,虽然基于MPE的PCA能够有效的区分四种状态,但将其与图9对比可以发现,基于MPE的PCA输出结果每一类各个样本的特征比较分散,聚类效果明显不如基于GCMPE方法。因此,GCMPE和MPE虽然都能有效地提取机械故障的特征信息,实现滚动轴承故障诊断,但与MPE相比,基于GCMPE的PCA降维处理后的主元分布更集中,聚类效果更好。上述对比分析结果表明,GCMPE不仅能够有效地提取滚动轴承故障特征,而且故障诊断效果优于MPE方法。 图9 基于GCMPE的PCA聚类结果Fig.9 Outputs of features based on GCMPE and PCA 图10 基于MPE的PCA聚类结果Fig.10 Output of samples based on MPE and PCA (1) 在排列熵的基础上,发展了广义复合多尺度排列熵(GCMPE),研究了GCMPE参数选择及影响,给出了GCMPE参数选择标准。通过分析噪声信号,将GCMPE与MPE进行了对比,结果表明GCMPE得到稳定值的一致性更好。 (2) 将GCMPE应用于滚动轴承试验数据分析,结果表明,GCMPE能够有效地区分滚动轴承故障类型,且区分效果要优于MPE。 (3) 提出了一种基于GCMPE,主元分析和支持向量机的滚动轴承故障诊断方法,试验数据分析结果验证了方法的有效性和优越性。1.2 多尺度排列熵
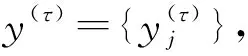
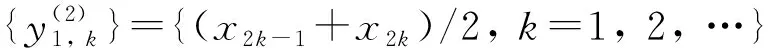
2 广义复合多尺度排列熵
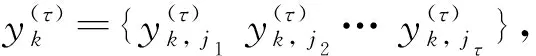
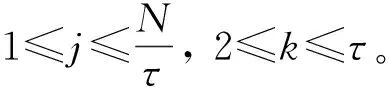
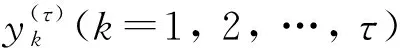
3 参数选择与对比分析
4 基于GCMPE,PCA与SVM的滚动轴承故障诊断方法
4.1 故障诊断方法
4.2 试验数据验证

5 结 论
