双足压电直线作动器结构优化与实验*

钟相强， 张本学， 黄卫清， 孙梦馨

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)(2.安徽工程大学机械与汽车工程学院 芜湖，241000) (3.广州大学机械与电气工程学院 广州，510006)

引 言

压电直线作动器因具有精度高和运动精确控制等优点而受到广泛关注，在某些场合下传统的作动器将无法进行正常工作，如低温、高温和电磁干扰的工作环境，而压电直线作动器的出现就是为了满足这些特殊环境要求[1-4]。柔性铰链因其没有间隙、没有机械摩擦和高的运动灵敏度等优点在压电直线作动器中得到广泛关注和应用[5-8]。

徐晶晶等[9]提出了一种三角和杠杆机构复合的压电直线电机，通过仿真和实验验证了该电机的运动轨迹正确性，但并未对复合机构放大率进行探讨，且该电机属于单足驱动型。

苏钊等[10]提出一种利用方波-三角波信号驱动的双足压电直线电机，讨论了不同驱动信号下电机的输出性能，但该电机中并未使用微位移放大机构。陈西府等[11]对动摩擦型压电叠堆单足直线电机定子的振动特性进行仿真和实验研究，推导了定子驱动端的振动微分方程，通过样机验证了该类型电机的谐振特性，但该直线电机采用压电叠堆直接驱动，并未使用微位移放大机构。

卢倩等[12-13]提出了一种二级杠杆式柔性铰链放大机构，推导出该柔性放大机构的放大率计算公式，通过引入柔度比来分析柔性铰链输出位移的灵敏度，经过优化获得最佳的位移放大率，但只是单纯研究二级杠杆柔性铰链计算优化，并未应用到压电直线作动器驱动。

基于二级杠杆放大原理，笔者对双足压电直线作动器作动原理进行分析，基于ANSYS Workbench对作动器定子结构相关参数进行优化仿真，最终构建了作动器定子的模型。通过实验测试获得该作动器的驱动足振幅，和理论计算相一致，为压电直线作动器的设计提供一种新的思路。

1 双足压电直线作动器的结构设计

1.1 二级杠杆放大原理

如图1所示，是二级杠杆放大原理图。结构由一个等臂杠杆和一个非等臂杠杆组成，其中，等臂杠杆输入位移，通过两个杠杆的连接部分(直圆型柔性铰链)传递至非等臂杠杆的输入端后，再次进行放大输出。因此，二级杠杆相比较一级杠杆而言，不仅能够得到足够大的放大倍数，而且空间占用率低。

图1 二级杠杆原理图Fig.1 Schematic diagram of secondary lever

对于单个杠杆AB而言，假设在杠杆AB的中点位置，即输入端输入一个数值大小为Din的位移，且位移的方向沿着图中输入端的箭头方向，则杠杆B点位置将对位移Din进行放大输出

(1)

对于杠杆AB和DE的连接部分，忽略其他因素，假设B点和C点处的位移量一致，即

xB=xC

(2)

对杠杆DE，E点的输出位移为

(3)

设λ为二级杠杆的放大倍数，则

(4)

式(4)中，L1，L2，L3和L4的数值分别为12，36，14和14 mm，将数值代入式(4)中得到二级杠杆的放大倍数λ为8。

柔性铰链放大倍数的第2种计算方法[12]

(5)

式(5)与式(4)的计算结果误差仅为2.6%，也证明了二级杠杆放大倍数计算的正确性。

1.2 压电直线作动器结构设计

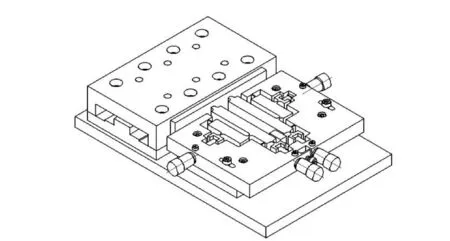
图2 压电直线作动器整体结构Fig.2 Overall structure of piezoelectric linear actuator

利用三维软件UG NX设计了二级杠杆放大式压电直线作动器结构[14-18]，如图2所示。其结构主要包括定子、动子、V型槽导轨、V型槽底座、耐磨陶瓷条、底板、预压件等；其中，定子通过螺钉与定位机构中的V型导轨连接，且定子还与定位机构中的V型槽进行活动连接，V型槽与底板连接；预压件主要包括预压块、预压螺钉和预压弹簧。预压件主要的作用是在松紧预压螺钉的过程中，驱使定子沿着V型槽进行轴向移动，调整压电直线作动器定子的驱动足与动子侧面上粘贴的耐磨陶瓷条之间的接触情况，使作动器的定子与陶瓷条之间产生预压力，以便于作动器与陶瓷条产生足够的摩擦力来驱动作动器移动。

图3所示为测微头与压电叠堆等之间的具体接触情况。压电叠堆的一端与定子中放大元件的初始输入端的面接触，另一端与方形垫块(绝缘体)接触；方形垫块具有半圆孔特征(放置接触小球)，测微头的平面输出端与接触小球接触，且测微头上具有螺纹特征，作用是与定子之间进行螺纹连接。压电叠堆需要在一定的预紧力下才能进行输出位移，通过旋转测微头能够给压电叠堆施加预紧力；测微头的输出端面为金属材料，添加绝缘体方形垫块是为了防止压电叠堆在工作时发生损坏；压电叠堆在使用时不能受到剪切力，而测微头的输出形式为旋转，所以在方形垫块上放置接触小球是为了将测微头的旋转输出转化为面接触的输出形式。

图3 测微头与压电叠堆等之间的具体接触图Fig.3 Specific contact diagram between micrometer head and piezoelectric stack

压电直线作动器定子作动仿真原理如图4所示。图中：(a)为驱动足I驱动导轨运动;(b)为驱动足II压紧导轨;(c)为驱动足II驱动导轨运动;(d)为驱动足I压紧导轨；I，II为作动器定子上的两个驱动足，作动器定子中使用的驱动元件(压电叠堆)共有四组。在一个周期内，导轨将沿着x轴正方向移动2α位移(此值为作动器的一个周期内的行程)。

图4 定子作动仿真过程Fig.4 Simulation process of stator actuator

1.3 压电直线作动器定子结构

双足压电直线作动器定子的结构如图5所示。四个压电叠堆通过相位差π/4的两正弦电压进行激励，使作动器定子系统产生振动，另外，椭圆运动轨迹在驱动端处形成。在预紧力调整机构的预压下，使作动器定子和动子之间产生摩擦力所需要的正压力，驱动动子进行运动[11]。

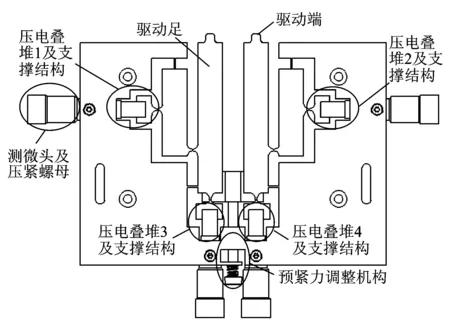
图5 双足压电直线作动器定子结构Fig.5 Stator structure of double-feet piezoelectric linear actuator

2 双足压电直线作动器的结构参数优化

2.1 基于ANSYS压电直线作动器定子的仿真

对压电直线作动器定子模型上四个沉头孔特征施加位移约束，作动器的定子材料为45#钢，其密度为7 850 kg·m-3，弹性模量为209 GPa，泊松比为0.3。对其进行有限元网格划分，节点数为91 591，单元数为50 370。

在压电叠堆输出端与定子结构的接触平面施加1 mm的位移驱动，来代替压电叠堆的变形输出。图6为作动器定子驱动足的输出位移云图。从图中可以看出，在1 mm约束驱动下定子的放大元件发生位移变化位置主要集中在定子驱动足上，其相应最大位移数值为7.360 mm，所以定子放大元件对输入1 mm位移作放大后输出为7.360 mm，其放大倍数为7.360，与上述理论值相差0.640 2，误差为8 %。

图6 定子驱动足的位移云图(1 mm)Fig.6 Displacement cloud picture of stator driving foot(1 mm)

在ANSYS中设置1 mm位移驱动，其目的是为了替代压电叠堆由于电压跳变而产生形变输出位移，实际上压电叠堆在输出位移的同时，相应地也会输出力，一般这个力的数值范围在0～1 000 N之间，所以还要模拟压电叠堆输出力时定子的放大能力。

图7 定子驱动足的位移云图(500 N)Fig.7 Displacement cloud picture of stator driving foot(500 N)

图7为500 N下的作动器定子驱动足的输出位移云图。从图中可以看出，在500 N力下定子发生位移变化位置主要集中在定子驱动足上，其相应最大位移数值为3.374 mm。500 N力载荷接触面上的最大位移数值为0.386 mm，所以作动器定子放大元件对500 N力的放大倍数约为8.741，此值与理论计算值相差0.741，误差为9.26%。

综上，经过软件仿真得到压电直线作动器定子的放大倍数误差分别为8%(1 mm)和9.26%(500 N)。造成仿真研究定子的放大能力误差有以下原因：a.理论计算所使用模型为结构简图，一定意义上并不考虑模型宽度和厚度等因素对其放大能力的影响；b.作动器定子的放大元件由两个杠杆及直圆型柔性铰链连接部分构成，而直圆型柔性铰链在作动器实际工作过程中并不只发生伸缩运动，还会因为承受力而产生弯矩或其他形变；c.在理论计算过程中，将除了直圆型柔性铰链中发生变形的地方，其他作动器定子结构统统看作刚体结构，但实际工作过程中，在理论分析中视作刚体的部分会吸收消耗一部分输入而发生变形现象，从而导致实际作动器定子放大元件的放大能力与理论计算值相比会出现缩减现象。

2.2 基于ANSYS的铰链参数优化

图8和图9为直圆型柔性铰链和直梁型柔性铰链的结构参数。图10为压电直线作动器定子结构单足驱动的简化模型，对于单个驱动足设计有四个柔性铰链，编号为1～4，其中柔性铰链的参数设定为Rh=1.77 mm，th=0.5 mm，bh=10 mm，lh=4.04 mm。

图8 直圆型柔性铰链的参数结构Fig.8 Parametric structure of straight circular flexure hinge

图9 直梁型柔性铰链的参数结构Fig.9 Parametric structure of straight beam flexure hinge

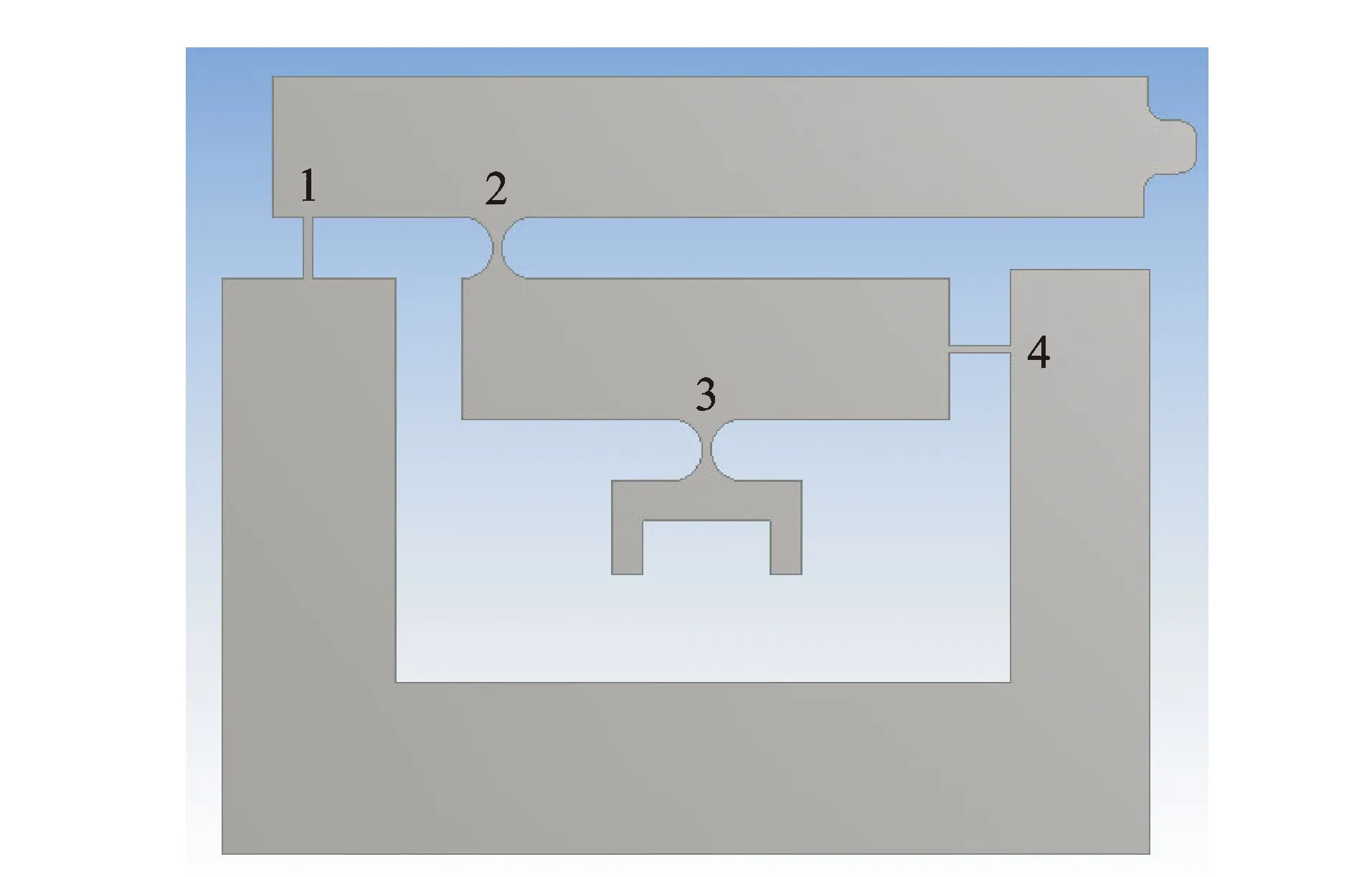
图10 柔性铰链编号Fig.10 Flexure hinge number

对于柔性铰链[12-13]的研究可知：直圆型和椭圆形柔性铰链的柔度比明显大于直梁型和倒圆角直梁型柔性铰链的柔度比，这说明当柔性铰链同时受到弯矩Mz和轴向力Fx作用时，直圆型柔性铰链和椭圆形柔性铰链则更容易产生线位移，而直梁型柔性铰链和倒圆角直梁型柔性铰链输出位移的主要形式是旋转位移。这一结论对于设计柔性微位移放大机构中柔性铰链的选型和设计具有很好的指导作用。

在压电叠堆输出位移的情况下，结合压电直线作动器定子的结构、二级杠杆放大机构的受力及变形情况的分析来看，图10中的1号和4号柔性铰链为直梁型柔性铰链，2号和3号柔性铰链使用直圆型柔性铰链，这是因为1号和4号处的柔性铰链在输出时主要产生旋转角位移，而产生的拉伸线位移相对较少；而2号和3号处的柔性铰链在输出时主要产生拉伸线位移，而产生的旋转角位移相对较少。

基于上述分析，在压电直线作动器定子的模型中使用直圆型柔性铰链和直梁型柔性铰链的混合搭配使用，会使压电直线作动器定子放大倍数得到优化，在缩小定子尺寸，提升定子驱动足刚度的前提下，可以得到较大的定子放大倍数。

2.3 基于ANSYS的参数优化过程

定子的放大倍数能力主要与1～4号铰链相关，故需要得到1～4号铰链的各个参数优化数据。对每个铰链的厚度和半径(1～4号柔性铰链切割半径全部约束相等，故只设置一个参数R1；厚度分别设置成参数T1，T2，T3和T4，数值相等)定义成参数形式(输入参数)，对定子模型3号柔性铰链处施加1 mm位移驱动，相对应获得定子末端驱动足上的位移输出，得到模型的初始放大倍数为7.399，并设置末端驱动足的位移输出作为输出参数(优化目标)。

铰链参数优化是通过改变铰链的参数时末端驱动足的位移输出达到最大值(即模型的放大倍数)，因为铰链的宽度直接设为bh=10 mm，只需设置切割半径和厚度为输入参数，铰链切割半径的变化范围为0.5～3.0 mm，步长0.25 mm；厚度的变化范围为0.2～1.0 mm，步长0.1 mm。

从ANSYS的DesignExploration模块分析结果得到结论：第95组数据中，2号直圆型柔性铰链厚度th=0.4 mm，lh=3.34，3号直圆型柔性铰链厚度th=0.2 mm，lh=3.34，1号直梁型柔性铰链厚度th=0.5 mm，lh=3.34，4号直梁型柔性铰链厚度th=0.6 mm，lh=3.34，对应的模型放大倍数为8.148，放大能力要比初始设定的铰链参数(th=0.5 mm，Rh=1.77)下的放大倍数7.399大。但由于考虑到压电直线作动器定子的刚度问题，为提高定子刚度，选择第96组数据，2号直圆型柔性铰链厚度th=0.4 mm，lh=3.34，3号直圆型柔性铰链厚度th=0.3 mm，lh=3.34，1号直梁型柔性铰链厚度th=0.5 mm，lh=3.34，4号直梁型柔性铰链厚度th=0.6 mm，lh=3.34，对应的模型放大倍数为8.131，相差仅0.017，能够满足使用要求。

3 双足压电直线作动器定子驱动足振幅实验

双足压电直线作动器定子驱动足振幅测试装置如图11所示。

1.Laser XL-80激光位移传感器；2.固定定子3的夹具；3.定子;4.定子的I号驱动足；5.定子的II号驱动足；6.压电叠堆(100 V，8.5 μm自由行程位移)图11 定子驱动足振幅测试装置Fig.11 Test device of stator driving foot amplitude

由信号发生器生成1路100 Hz的正弦波信号，并由信号放大器将电压放大至120 V，驱动定子驱动足进行工作，激光位移传感器读取驱动足的位移并将数据传输到相应PC机上。

实验测得两个驱动足的位移数据如图12,13所示。从图中可以看出，两驱动足的振动相对稳定，驱动足I,II的位移幅值在60和63 μm的上下范围浮动，差值约为3 μm，至于造成此差值的可能原因有：a.压电叠堆预紧力不一致；b.所使用的压电叠堆的输出性能不一；c.加工误差导致两驱动足性能不一致；d.测量方法不精确导致的测量误差；e.测量过程中出现的随机误差。

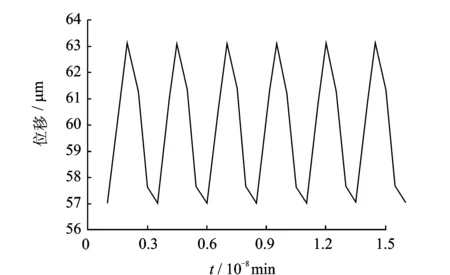
图12 驱动足I的振幅Fig.12 Amplitude of driving foot I

图13 驱动足II的振幅Fig.13 Amplitude of driving foot II

通过实验测得驱动机构(驱动足I)的位移幅值在8.2 μm上下范围浮动，经过定子中放大元件放大此位移后由驱动足I输出，数值约为60 μm，所以放大元件的放大能力约为7.32，这与上述理论计算和仿真研究得到的放大倍数都要小，基本符合要求。造成这一现象的可能原因有：a.定子的整体刚度较弱而导致在实验过程中发生变形；b.测量误差。

4 结 论

1) 提出一种基于二级杠杆和柔性铰链复合结构的双足压电直线作动器，通过两种方法计算出该二级杠杆的理论放大倍数，两者的误差仅为0.209，证实了该二级杠杆设计的正确性。

2) 基于ANSYS完成压电直线作动器定子作动仿真过程，通过在压电叠堆输出端与定子结构的接触平面施加相应的位移驱动和驱动力，仿真得到放大倍数与理论计算之间的误差分别为8%和9.26%，和理论计算相符合。

3) 通过仿真分析发现，在压电直线作动器定子中使用直圆型柔性铰链和直梁型柔性铰链，会使作动器定子放大倍数得到优化，在提升定子驱动足刚度的前提下，可以得到较大的放大倍数。

4) 基于最优化参数制作了该作动器样机，对作动器驱动足振幅进行了实验测试，两驱动足的振动相对稳定，驱动足I,II的位移幅值在60和63 μm的上下范围浮动，测得定子放大元件的放大能力约为7.32，比理论计算值偏小，与实验中定子整体刚度和测量误差有关系，后期可在保证振幅放大倍数的前提下进一步优化作动器的特性。