基于奇异峰态的钢轨踏面损伤弦测特征辨识*

殷 华， 朱洪涛

(1.江西农业大学软件学院 南昌，330045) (2.南昌大学机电工程学院 南昌，330096)

引 言

经过长时间运营后，钢轨踏面通常会出现各种不规律的损伤，包括擦伤、剥落、缺损等[1-2]。当高速运行的列车轮对通过有损伤的钢轨踏面时会有巨大的轮轨冲击力，进一步加剧其损伤程度，并有可能造成列车轮对踏面出现扁疤，产生轮轨噪声，影响列车运行的质量，严重时更可引起钢轨断裂，给人民群众生命财产带来损失[3]。虽然国内外学者对钢轨踏面损伤进行了诸多研究，给出了其产生的可能原因及对策，但是钢轨踏面损伤却不能完全避免[4]。与核伤不同，钢轨踏面的这种损伤并不是没有任何征兆直接出现的，从最初的踏面外形磨损变化到表面出现微裂纹，并进一步恶化成为疲劳裂纹最终导致出现剥落掉块等严重病害需要一定的时间[5]。在这种情况下，如何对钢轨踏面状态进行检测，以期尽可能早的发现存在的问题成为关键。目前,铁路工务中对这些踏面损伤常采用人工目视巡检，发现病害后再利用平直尺或半自动式钢轨轮廓检查仪进行定量手工测量，这种方法劳动强度大，且人工巡检容易忽视初期产生的微小损伤；另一种更为可靠的方式是在轨道检查车上安装有两个呈一定角度放置的线激光传感器，采集轨道廓形数据，并进行旋转平移后与标准值比对得到各部分的磨损量，显然其也能检测踏面损伤。这种方法得到的结果虽然准确，但其成本过于高昂，不利于推广使用，并且受到采样间距的限制有可能出现漏检[6-7]。另外，还有利用机器视觉或超声波等获取钢轨踏面信息后，再进行特征提取和损伤辨识的方法[8-10]。在理想情况下其准确度尚可接受，但铁路轨道现场情况通常比较复杂，这些手段容易受到周围环境的影响而准确度降低。除此之外，上述所有测试方法都需要借助额外的测量设备，既增加了测量成本，也不利于铁路工务中的快速作业的需求。

弦测是当前铁路轨道不平顺中、长波测量中广泛采用的手段，而文献[11]给出了多中点弦测理论的轨道短波测量方法，这使得弦测法具有更广阔的应用前景。由于弦测法通常以轨道光带中线为测量目标，而踏面损伤亦多发生在该处，因此在采样率足够的前提下，弦测法应当能够对轨道踏面不规律的损伤有所响应。笔者在分析弦测法原理基础上提出了多弦测量理论下的钢轨踏面损伤检测方法，在不增加任何硬件成本的前提下，仅对轨道检查弦测小车结果数据进行分析就能辨识出踏面微小损伤及其具体位置，为轨道日常巡检及养护提供依据。

1 中点弦测法及特点

1.1 基本原理

中点弦测法是指在钢轨踏面上任意两点放置一根固定长度的刚性弦，在弦的中点位置安装距离传感器，探头正对钢轨踏面，该探头到钢轨踏面的距离记为中点弦测值。将刚性弦沿轨道方向移动，即可得到中点弦测序列。若设当前轨道不平顺函数为F(X)，则距离传感器测得的钢轨不平顺幅值Δ可用下式来表示：

(1)

其中：L为刚性弦的长度。

对式(1)进行频域变换，可得传递函数

(2)

其中：ω=2π/λ为空间角频率；λ为被测轨道的波长；φL(ω)为零表明经过中点弦测量后的数据与原始数据相位一致；HL(ω)说明轨道线路不平顺进行弦测后，其幅值增益在0～2之间变换，但只要保证具有幅值响应，利用中点弦测数据就有可能实现对当前钢轨上存在的各种波长病害进行检测。

1.2 踏面损伤的中点弦测响应

从信号的角度来看，若函数x(t)在某点间断或某阶导数不连续，则称函数在该点具有奇异性，常用Lipschitz指数α来描述：某点的光滑度越高其α值越大；反之则α值越小[12]；状态良好的钢轨踏面通常都是平顺的，当不规律的剥落掉块等损伤出现时可认为是平顺轨道上的奇异点，会呈现出不连续奇异特征[13]。因此，当某条轨道线路出现钢轨踏面损伤后，其状态可近似表示为本身具有的不平顺与奇异信号的叠加，如式(3)所示：

(3)

其中：f(X)表示轨道本身具有的不平顺；n表示该轨道上所具有踏面损伤的数量；θ(X-ti)表示在ti位置上踏面发生了损伤。

在该轨道上利用中点弦测法进行测量，结果可用式(4)表示：

(4)

其中：Δ′表示经过中点弦测量后的结果。

从式(4)可知,原有的n处钢轨踏面损伤在经过中点弦测量后变动了3n处，其位置分别为ti-L/2,ti以及ti+L/2，并且在ti处的踏面损伤测量值符号与其他两处相反。这表明，具有踏面损伤的钢轨在经过中点弦测后，所得结果依然会包含有损伤的幅度及位置信息，但幅值仅在ti处保持不变，而在其他两处均被压缩为原始幅值的1/2。在理想状态下，当损伤的幅度大于轨道本身具有的不平顺时，采用小波变换等时频算法即可对该损伤从频率的角度进行辨识。但钢轨踏面损伤的初期，其损伤的幅度并不会明显大于轨道本身不平顺，特别是在一些具有波浪磨耗的线路上，根据式(2)，当πL/λ满足式(5)(其中k为正整数)时, 中点弦测法的幅值增益将大于1,会把轨道本身的不平顺值放大,而踏面损伤则基本保持不变。这将使得钢轨踏面出现的损伤在经过中点弦测后有可能被淹没，无法辨识。

(5)

2 多中点弦测法及其踏面损伤响应

根据前面分析，中点弦测法有可能将钢轨踏面损伤淹没的原因是其对轨道本身不平顺幅度放大的同时却没有对踏面损伤的部分进行处理。若能找到一种方法反其道而行之，将钢轨踏面损伤幅值放大，而抑制轨道不平顺本身的中点弦测结果，则有可能使得踏面损伤特征更加突出，有利于后续准确辨识。观察式(4)，具有踏面损伤的钢轨弦测结果可以分为3个部分的线性叠加：原始不平顺响应(式(4)中的前两项)、踏面损伤偏移响应(式(4)中的第3，4项)及踏面损伤响应(式(4)中的最后一项)。由于踏面损伤偏移响应的相位和幅值均发生了变化，故实际测量只需考虑对踏面损伤响应部分进行放大且抑制原始不平顺响应即可。而从式(2)可知，中点弦测法的幅值增益-波长响应曲线与测量弦长有直接关系。如果能将多个中点弦测结果相加，则有可能实现上述目标。此时，弦测结果可简化表示为

(6)

其中：m表示为中点弦的数量；LK为第K个中点弦的长度;Δ″为采用多中点弦测量后的结果。

式(6)说明，对于弦测结果的原始不平顺响应部分只要找到合适的多弦组合，使得多个中点弦测结果之和对所有波长的增益尽可能的小即可。此时，幅值将并不会随着弦数量的增加而等比例放大，但踏面损伤响应部分的幅值却和中点弦的数量呈倍数关系：测量所采样的中点弦组合越多，钢轨踏面损伤检测结果就越大。图1是在内部实验轨道上人为添加模拟剥落掉块损伤后，采用双中点弦测小车进行推行实验所获取的弦测数据。轨道本身的不平顺在0.1 mm以下，为了便于观察，模拟焊缝的高度设置为0.7 mm大于轨道本身。从图中可以看出，弦测法对轨道上的损伤是有响应的，对于单弦测量，在其测量结果中出现了3处突变，分别代表了不同测头经过该模拟焊缝时的响应；而对于双弦测量，测头的数量增加为5个，其测量结果也出现了5处响应。但不论是哪种测量方式，由于具有相位不变的特性，中心测头处始终提示有突变，幅值是两侧测头的2倍；且当采用双弦组合时，中心测头所得幅值变为了两个独立的单弦测量值的叠加，为两侧测头的4倍。这从实验中验证了前面关于多中点弦测法对钢轨踏面损伤的响应分析。

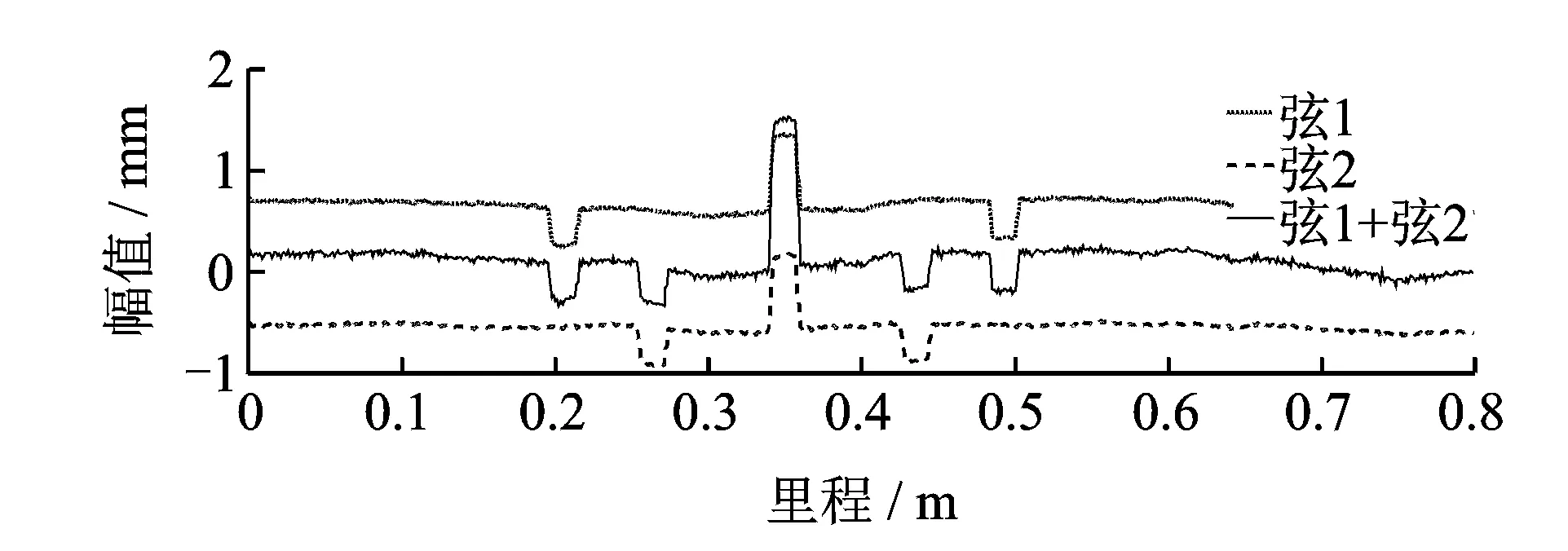
图1 模拟踏面损伤轨道双弦测量结果Fig.1 Result of double chord measurement on surface defects track

3 奇异峰态踏面损伤特征辨识

虽然利用多中点弦测能够将轨道踏面上的损伤放大，但由于放大倍数与弦的数量有直接关系，而弦的数量与高精度传感器又需要满足S=2s+1(S表示传感器的数量，s表示中点弦的数量)。当采用过多的弦时，测量设备既不具备成本优势，也容易造成制造过程中出现较高的不良率。因此，为了满足工程应用需要，弦的数量应该在3根及以下。此时虽然钢轨踏面损伤幅度已经被放大了数倍，相比较于单弦测量结果更加易于识别，但仍有可能被钢轨本身测量值淹没。因此，需要找到一种有效的方法对该增强后的踏面损伤信号进行进一步分离。

3.1 奇异值分解原理

奇异值分解(singular value decomposition，简称SVD)是近年发展起来的基于数学形态学的一种算法，其在机械故障诊断、降噪方面都有很好的运用。基本思想是：任意的m×n矩阵A通过奇异值分解后都能变换为3个矩阵的乘积

A=UΣVT

(7)

其中：U为m×m阶酉矩阵；V为n×n阶酉矩阵；Σ为对角方阵，其值在对角线上按照从大到小排列，称为矩阵A的奇异值[14]。

奇异值分解是一种基于矩阵变换的算法，而轨道弦测数据是一维的里程序列，这就要求在奇异值分解之前将该序列通过某种方法构造成为矩阵。文献[15-16]对该问题进行了详细的分析，指出当把序列构造成Hankel矩阵时，奇异值分解后的第Z个分量具有Z-1阶消失矩，能够辨识不同类型的奇异信号；各类奇异信号在不同分量中会近似以冲击信号特征显示；第Z+1个分量中会包含有前面Z个分量的信息，并且各个分量中奇异信号所处的位置不变。由于多弦测量后的轨道踏面损伤对于轨道不平顺本身来说仍然保持其奇异特征，那么若将整个轨道的多弦测量结果进行奇异值分解，则各个分量也必然包含有各类不同踏面损伤特征。

3.2 滑动峰态算法

虽然奇异值分解后分量中能以近似冲击信号特征体现出钢轨踏面损伤及位置，但分量的幅值与整条轨道的不平顺程度有关，这对于工程应用中如何用数值界定病害是否出现及其严重程度是非常不利的。通常而言，踏面损伤越严重，其表现出的测量结果奇异性就越强，波形越陡峭，反之则越平稳。高阶累积量是统计信号处理中一类非常重要的反映信号非高斯分布特性的方法，其中4阶累积量具有零均值、零时滞，被定义为

C4x=E[x4(n)]-3{E(x2(n))}2

(8)

其中：x(n)为平稳随机过程，n=…,-2,-1,0,1,2, …。

将C4x除以均方差的4次方可用来描述随机序列概率分布曲线尖或平的程度，又被称为峰态。由于冲击信号具有明显的非高斯分布特性，故其峰态分布具有尖尾和平尾特性。基于该特性，文献[17]使用了一种滑动峰态算法，其设置一个长度为P的滑动窗，通过每次对该滑动窗内的数据计算峰态值，可以得到一个峰态序列，若原始信号中包含有冲击成份，则峰态序列必然在同一位置有对应的峰值。将滑动峰态算法引入到轨道踏面损伤弦测结果的分析中，当对钢轨踏面损伤弦测数据的奇异值分量计算得到峰态序列后，应当能够将踏面损伤特征分离，并可以根据峰态值的大小设定阈值，便于工程应用。

由此，可以得到辨识钢轨踏面损伤的具体方法，步骤如下。

1) 选定合适的弦长组合构成多中点弦测系统对目标轨道进行测量，若钢轨上包含有踏面损伤带来的奇异特征，则得到的弦测序列中该特征幅值会被放大s倍(s表示中点弦的数量)。

2) 对弦测序列构造hankel矩阵，进行奇异值分解，得到分解后的多个分量序列。

3) 选取奇异分量序列，采用滑动峰态算法计算该分量的峰态序列。若轨道踏面存在损伤，则该峰态序列对应的位置将出现一个尖峰且其陡峭程度与损伤的程度有直接关系。

4 系统仿真验证

上述分析均基于理论，有必要在理想的环境下对方法的可行性、正确性进行验证。为了尽可能的与真实轨道保持一致，采用文献中的方法，利用多个数量、相位、幅度、波长随机的正弦波复合对轨道进行数值模拟，并使其符合文献规定的标准轨道功率谱，再叠加信噪比为20 dB的噪声[18]。模拟轨道波形如图2所示，其长度为5 m，在里程约为2和3 m位置分别出现两处微小损伤，宽度不超过4 mm，深度随机产生但不超过0.01 mm。

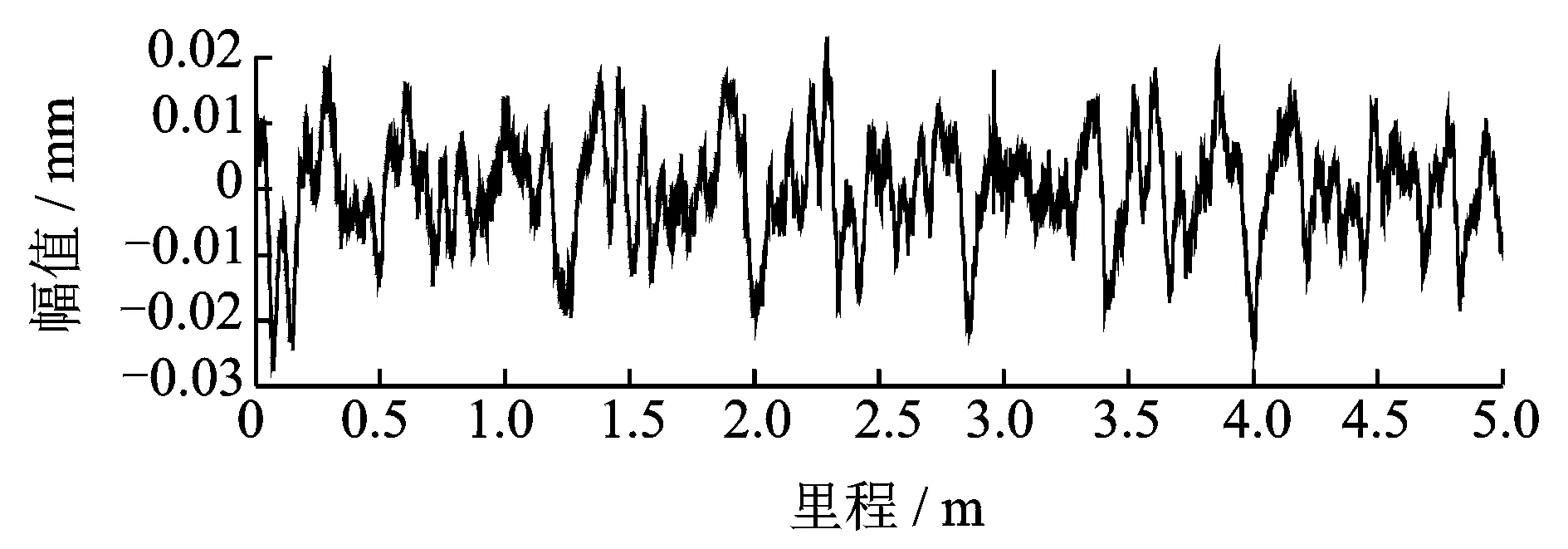
图2 仿真轨道波形Fig.2 Simulation track waveform

选取双中点弦理论中常用的174和292 mm弦长构成双测量弦结构，设置采样间距为1 mm，对该轨道进行仿真测量。此时该双弦结构最大幅值增益为1.7，增益标准差约为0.45，故踏面损伤冲击幅值放大倍数将超过轨道本身的不平顺。图3为双弦结构的检测结果。

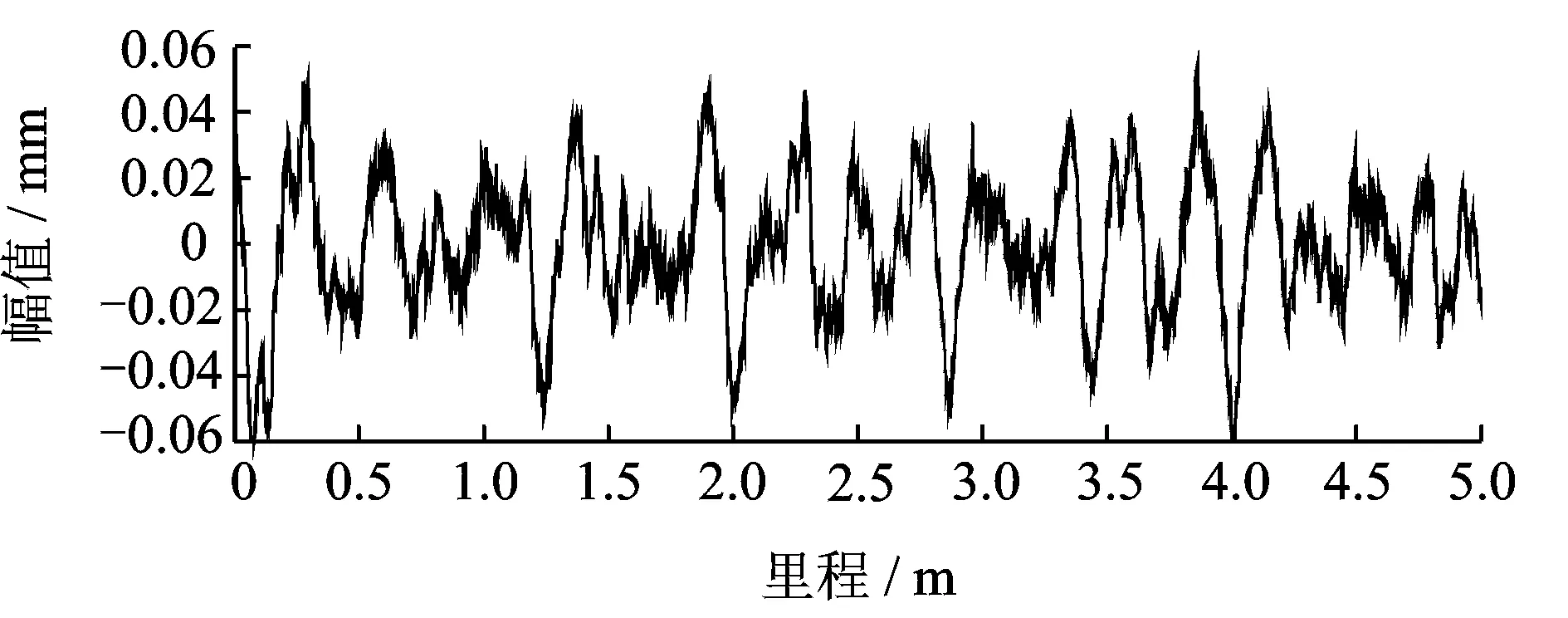
图3 模拟轨道双弦测量结果Fig.3 Result of double chord measurement on simulation track

从图2、图3可知，不论是在原始轨道波形还是在双弦测量结果中，由于两处损伤幅值过于微小，被淹没于轨道本身不平顺中，直接观察是很难发现它们的存在。对双弦测量结果进行奇异值分解，考虑到轨道踏面损伤有可能还会出现一阶导数不连续的奇异特征，根据文献[15-16]分解阶数设定为6，并取出第3个分量可得图4。图中出现了两处幅值较大的尖峰，恰好是原始轨道中的轨道模拟踏面损伤位置，它们被该分量辨别出来。

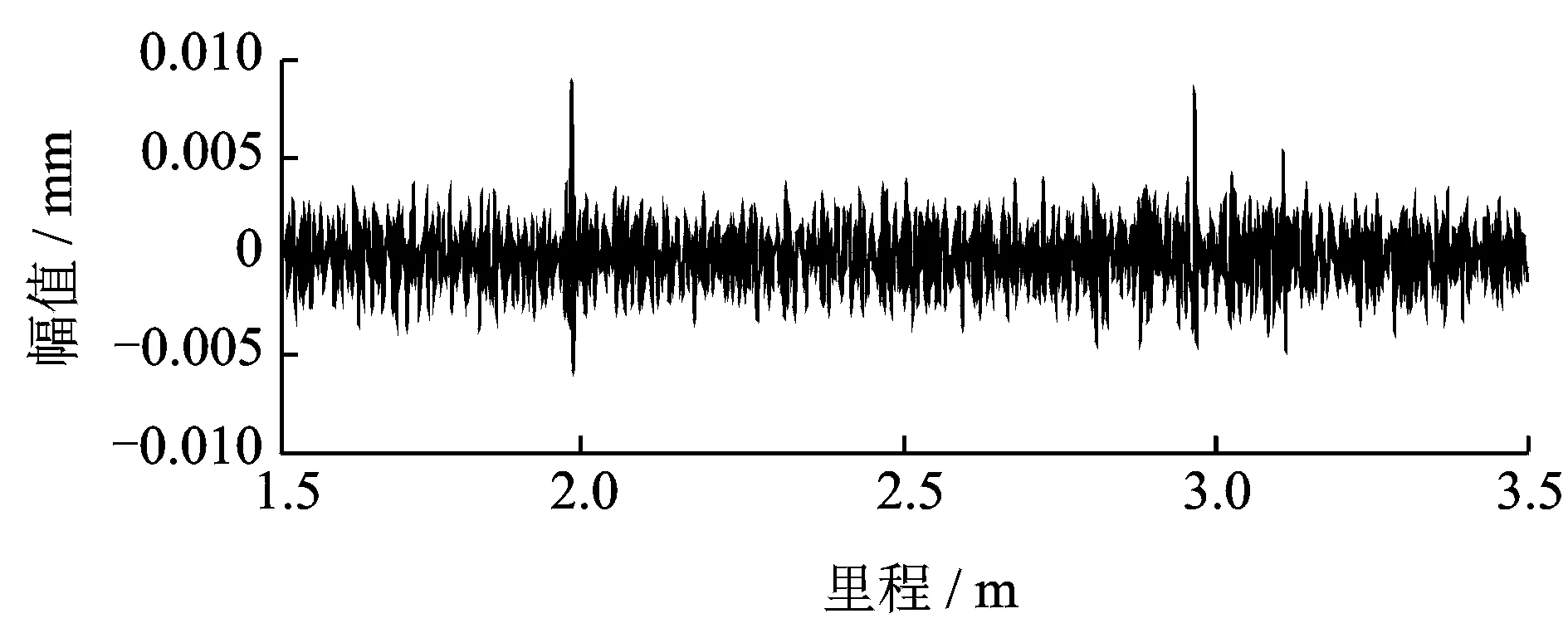
图4 模拟轨道奇异值分解第3个分量波形Fig.4 Third component of simulation track after singular value decomposition

对图4数据求其峰态序列，考虑到噪声及轨道本身不平顺的影响，滑动窗不能取得过小，由于双弦中最短弦长为174 mm，不妨以174 mm作为滑动窗的长度计算得到图5。从图5中可以看出，峰态序列中有两处幅值显然大于周围数据的区域，且它们的长度都为174 mm。这是由于一旦滑动窗中包含有图4的突变部分数据时其峰态值将会显著增加，这个过程会一直维持到滑动窗中不包含有突变部分为止。因此，结合奇异值分量和对应的峰态序列就能很好地确定轨道踏面损伤的位置。

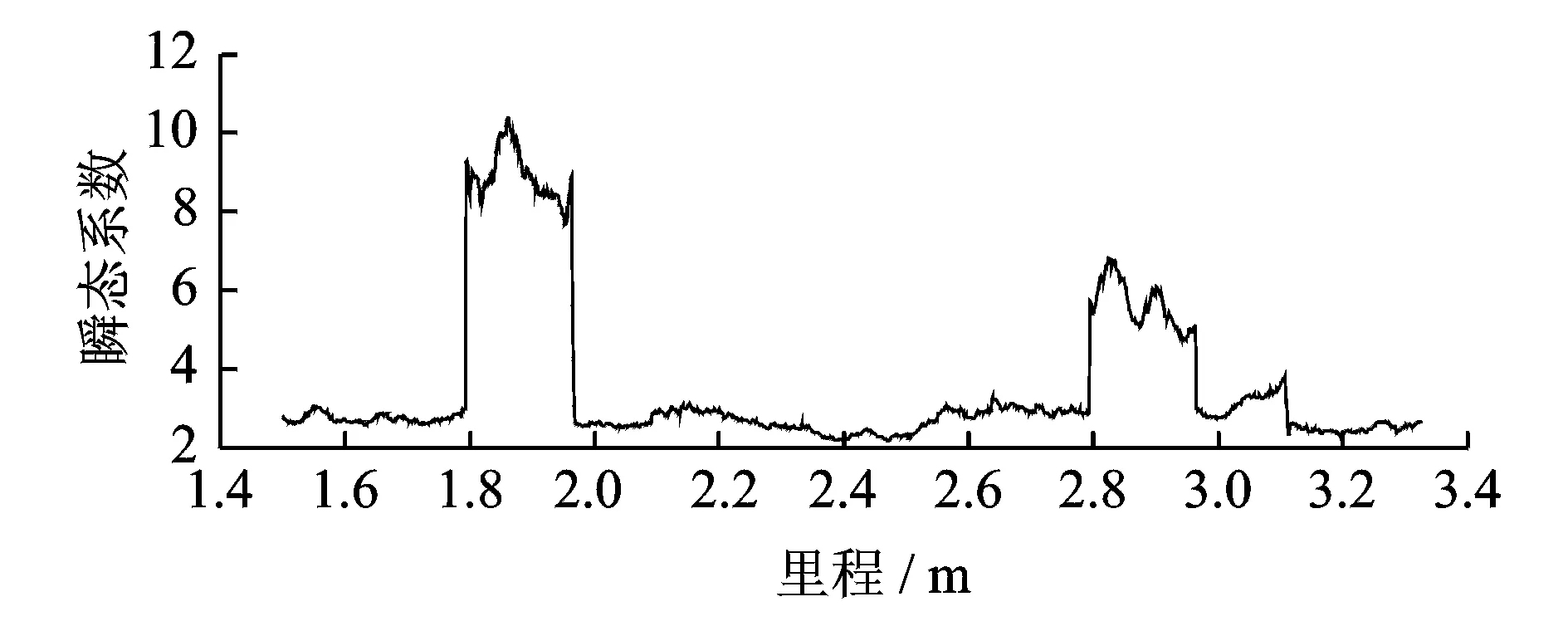
图5 模拟轨道第3分量的滑动峰态系数序列Fig.5 The sliding kurtosis result of third component based on simulation track

5 线路实测

实际线路轨道通常比较复杂，其中存在着测量噪声等诸多干扰因素，有必要在实际轨道线路中验证方法的有效性。实验线路选择鹰厦线K52+700±50区间。该段线路为夹直线，轨道上常年客货混跑，线路状态较为复杂，钢轨踏面上的剥落掉块时有发生。图6为双弦测量实验小车及具有踏面损伤的真实轨道，小车的5个测头安装于车体内部，且正对钢轨踏面中线位置，因此所得数据中将仅包含图中红圈处的伤损信息。

图6 弦测小车及包含踏面伤损的实际轨道线路Fig.6 Chord measuring equipment and defective surface on actual track

测量小车双弦长度分别为174+292 mm，从距离该踏面损伤约10 m处推行。测量数据通过5个基恩士IL-100激光位移传感器同步采集获得，如图7所示，在该数据中很难发现有踏面损伤信息。

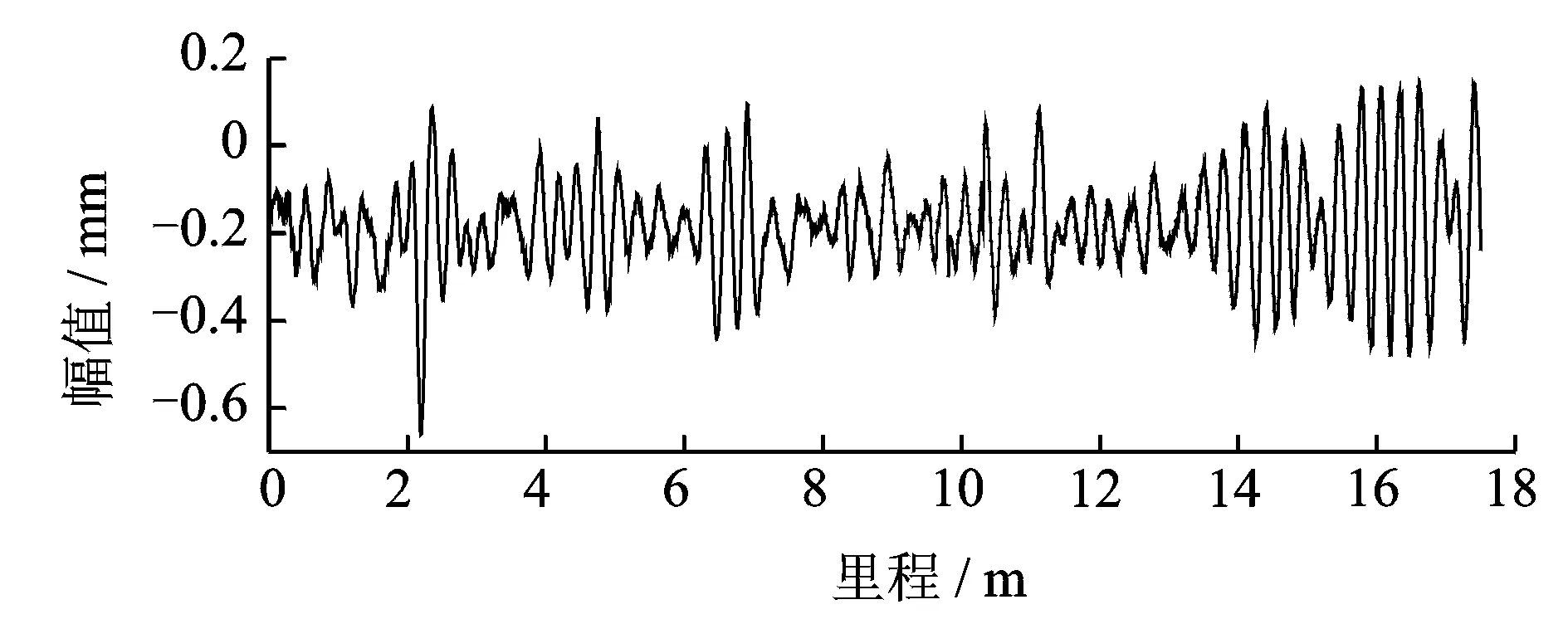
图7 真实轨道双弦测量数据Fig.7 Double chord measurement based upon actual track

对该测量数据同样进行阶数为6的奇异值分解后得到第3分量，即原始测量数据中不连续的点，如图8所示，对该分量信号求峰态序列得到图9。两图中对轨道踏面损伤信息均有提示，但相对于图8，图9更加有利于人工和程序辨识，更具有实际意义。

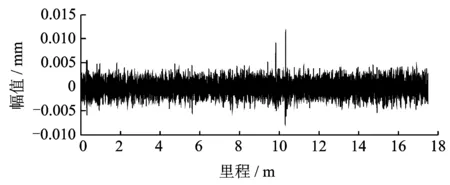
图8 真实轨道奇异值分解第3分量Fig.8 Third component of actual track after singular value decomposition

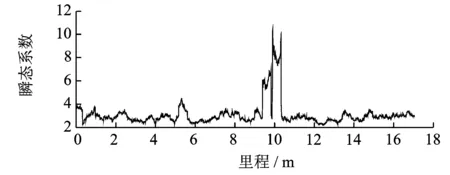
图9 真实轨道第3分量滑动峰态系数序列Fig.9 The sliding kurtosis sequence of third component based on actual track

6 结束语

从信号角度来看，钢轨踏面损伤近似于轨道上出现的奇异点，经过弦测后依然能够保持其奇异性。采用多弦测量能够增强踏面损伤的弦测响应幅度，且放大倍数与弦的数量有关。这更有利于钢轨踏面微小损伤的辨识。理论仿真和线路实测表明：在不过多增加硬件成本的前提下，对弦测数据进行奇异值分解后，再求出对应分量的滑动峰态系数序列就能够辨识出弦测结果中隐含的踏面损伤信息，具有良好工程应用前景。