桁架式火星探测器的着陆缓冲特性分析*

陈传志， 魏 君， 陈金宝， 聂 宏， 郑 光， 袁英男

(1.南京航空航天大学航天学院 南京，210016) (2.南京航空航天大学航空宇航学院 南京，210016)

引 言

软着陆缓冲机构是行星探测器着陆过程中最重要的吸能装置，其主要功能是缓冲探测器在行星着陆时的冲击载荷，保证结构和有效载荷的安全，防止探测器倾倒并为其在行星工作时提供支撑。目前，常用的着陆缓冲系统有气囊式和机械式两种。气囊式缓冲系统的结构形简单，通过气囊内部气体的压缩做功来吸收着陆器的功能，经过多次弹跳后将初始动能逐步耗散，适合火星表面有大气压力且地貌复杂的着陆工况。机械式缓冲系统着陆姿态便于控制，且通过缓冲器阻尼特性的设计可以避免着陆过程中的巨大反弹，适用于着陆体积和质量较大，以及着陆后需要返回的探测器软着陆。桁架缓冲结构是机械式缓冲系统中最具代表性的一种，具有重量轻、结构受力合理、材料利用率高等优点。美国Surveyor系列无人月球探测器和Apollo系列载人月球探测器的缓冲装置均采用了桁架结构[1]。该结构采用了多种缓冲方法，包括多胞材料变形法、薄壁管金属管变形法、金属切削法及金属杆拉伸变形法等。

自20世纪60年代以来，月球探测器软着陆过程动力学研究已经在国内广泛展开[2-3]。随着嫦娥三号探测器在月面的成功着陆，中国的航天计划已经将目标转向了更远的火星。根据披露的火星探测计划，整个探测任务将于我国“十三五”计划末正式启动，技术难度和跨度将比目前我国的月球探测任务更大。目前，世界上多个国家和地区已开展了大量关于火星探测的科学研究[4-5]，其中，前苏联、美国、欧盟已先后实现航天器火星表面着陆，中国的火星探测势在必行。

迄今为止，大多数月球和行星探测器采用气囊式缓冲、铝蜂窝缓冲和液压/气压缓冲的形式[6]，文中的着陆器缓冲装置采用金属杆拉伸变形法，利用金属拉杆的塑性拉伸变形来吸收冲击时的大部分能量。为分析缓冲性能，在瞬态动力学分析软件Dytran中对着陆冲击过程进行仿真计算，将仿真结果与实验数据对比，分析着陆器的缓冲性能，为我国今后的火星探测工作提供依据。

1 着陆缓冲装置构型及缓冲原理

大多数月球和行星探测器均采用腿式着陆缓冲机构，着陆腿围绕着陆器中心轴对称分布，我国公布的火星探测器构型如图1所示。文中的着陆器模型即为此构型，四条着陆腿沿周向均布，每条着陆腿均由两根多功能支柱、一根支撑支柱、足垫和压紧释放装置四部分组成。两根多功能支柱完全相同，具备展开、收拢和缓冲、吸能功能，支撑杆仅起到维持构型的功能。多功能支柱上端通过万向节与着陆巡视器结构相连接，多功能支柱下端通过球铰与足垫相连；支撑支柱上端通过限力杆与结构相连接，支撑支柱下端通过接头与足垫固连；足垫为帽型结构。

图1 我国公布的火星着陆器外观Fig.1 The appearance of Mars lander released in China

单套缓冲装置如图2所示，每条多功能支柱内均有两根关于支柱中心轴对称的拉杆，金属拉杆在内筒相对外筒向里运动时会受到因金属杆位置限制而引起的缓冲拉力F，当作用力F使金属杆的拉应力超过其屈服极限时，金属杆就会产生塑性变形，吸收相应的冲击能量，从而达到缓冲目的。

图2 单腿简化模型Fig.2 The simplified model of single leg

2 非线性有限元的显式积分法

非线性有限元动力学模型的数值解法，是将分布空间域进行离散，对于瞬态动力学问题，还要在时间域上进行离散，把连续的微分方程转换成有限阶的代数方程组

(1)

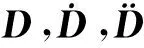
根据有限元理论建立起模型结构的质量矩阵、阻尼矩阵及刚度矩阵可求解式(1)，而对于求解时间域上的瞬态动力学问题时需在时间域上离散，通常采用显示积分算法求解。

假设当前步为第n步，将式(1)改写为

(2)

(3)

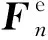
若将单元质量分布在节点上，则M为一对角阵，那么线性方程组将成为关于各自由度的一元一次方程，从而可以求解出加速度。

在时间域上假设加速度在一个时间步长内是恒定的，采用中心差分法可以得到

对模型的初始边界条件和运动进行约束后，通过式(4)和(5)求解出第n+1个离散时间点时各个离散节点处的位移dn+1、速度vn+1/2和加速度an。

3 火星着陆器有限元仿真建模

3.1 着陆器的有限元建模

在Patran中建立着陆器的有限元网格模型，对着陆器仿真过程影响不大的部位进行简化处理。仿真过程的最小步长取决于模型中的最小网格单元，对于一些对仿真结果准确性影响不大的细小单元采用质量放大方法人为提高材料密度[7]，提高仿真计算速度。

火星车(顶部长方体)采用一个等效质量的Hex8体单元模拟，舱的厚度较另外两方向尺寸小，故采用壳单元建模，模型中对舱体和简化的火星车做刚化处理，不用考虑其变形，舱和火星车利用多点约束(multi-points constrant,简称MPC)进行连接；多功能支柱内外筒壁厚较薄，因此采用壳单元；缓冲用拉杆为梁单元，本构模型采用DYMAT24分段线型塑性材料，拉杆材料为钢，密度为7 850 kg/m3，泊松比为0.27，弹性模量依据其应力应变曲线输入场；支撑支柱与舱面连接处限力杆采用实体单元建模；帽形足垫用一层壳单元模拟，足垫与火壤接触处的网格增大密度以提高计算效率。着陆器的有限元模型如图3所示。

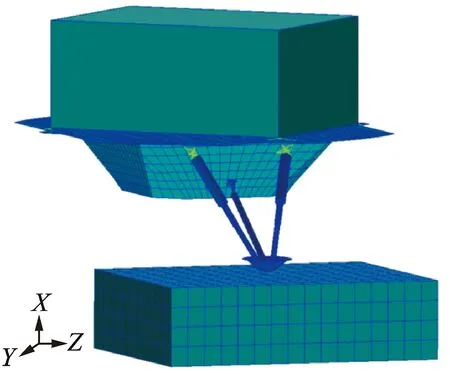
图3 着陆器有限元模型Fig.3 The finite element model of mars landing

在多功能内筒与外筒之间建立面面接触保证缓冲过程内筒沿外筒轴线方向运动；拉杆与筒壁之间建立点面接触从而实现拉杆的缓冲。为模拟单腿两侧多功能支柱球铰和万向铰相邻构件的接触情况，采用节点耦合法比较适宜。模拟球铰时，在球铰中心建立一个节点，采用杆单元分别与内筒末端和足垫壁相连，相当于建立一个可以转动的铰；模拟万向铰时，采用梁单元建立交叉的十字梁，十字梁与两端结构通过杆单元相连，球铰和万向铰如图4所示。

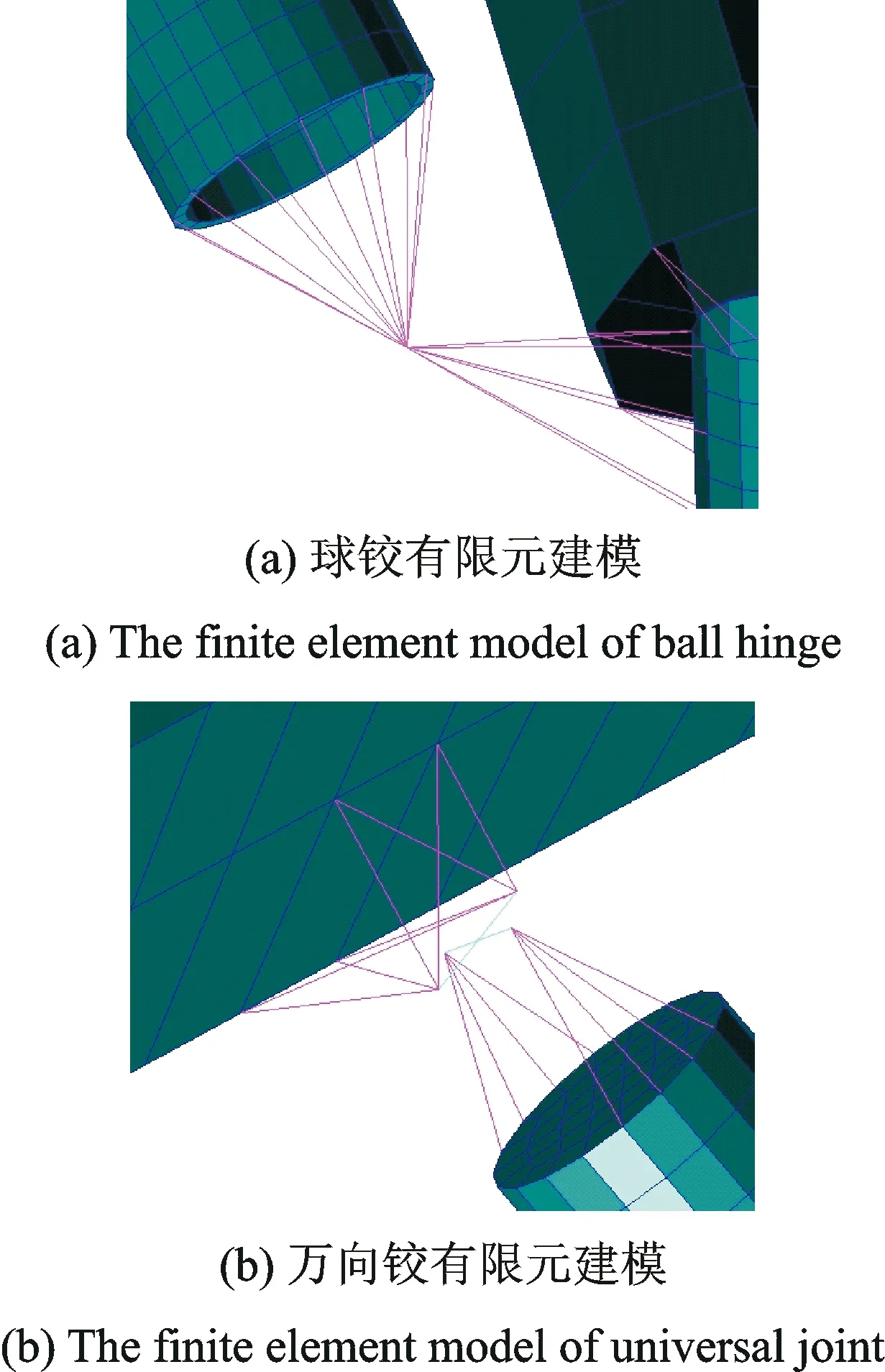
图4 球铰与万向铰有限元建模Fig.4 The finite element model of ball hinge and universal joint

中间支撑支柱限力杆下端通过十字梁结构与支撑支柱上端连接，限力杆与舱面通过梁单元连接，限力杆模型如图5所示。

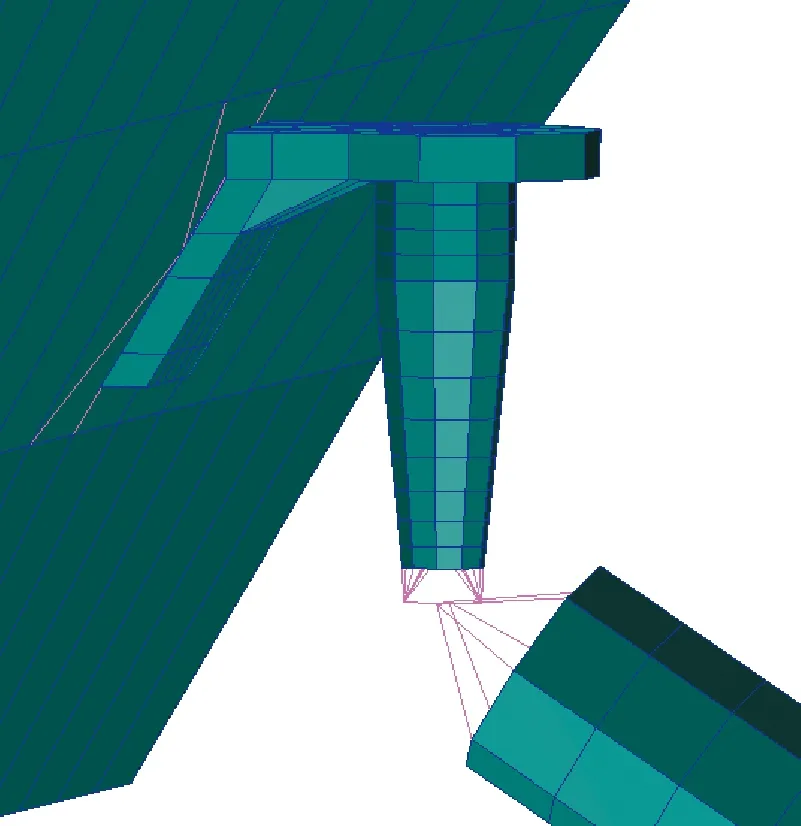
图5 限力杆有限元模型Fig.5 The finite element model of constrained-rod

3.2 火壤柔性化参数定义

除了直接利用探测器对火壤表面进行探测之外，地面也进行模拟火壤的研制，研制的国家和地区主要是美国、欧盟以及中国。工程应用中几种比较典型的模拟火壤有JSC MARS-1[8]，MMS(Mojave Mars Simulant)[9]，Salten Skov I[10]等。

火壤建模时材料采用试验用火壤模型，以便于和试验数据对比。在Dytran中采用DMATEL 本构模型对着陆面进行建模，材料密度为1 300 kg/m3，弹性模量为5.4×1010，泊松比为0.3，试验用火壤满足火星表面软着陆冲击裕度要求。

4 单腿着陆冲击仿真及试验

4.1 着陆冲击试验装置

火星着陆器单腿着陆冲击试验方案与月球嫦娥三号月球着陆器单腿试验方案相似。单腿着陆冲击试验装置[11]如图6所示，吊篮用于模拟着陆腿的安装，配重装置用于控制不同的着陆质量，着陆腿的投放高度由起吊装置控制。着陆平台和多功能支柱与吊篮连接的万向铰上均有测力传感器。

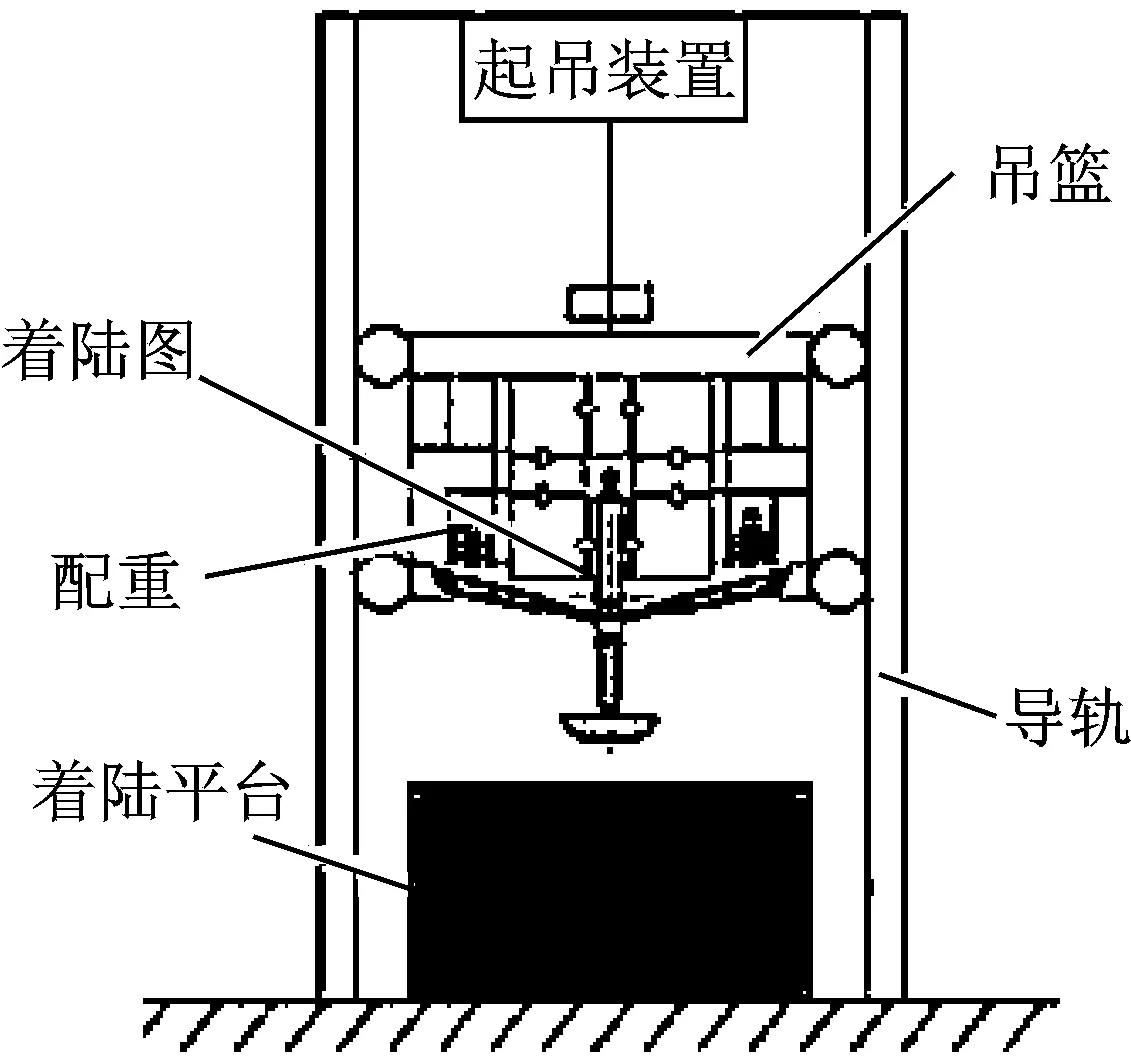
图6 单腿着陆冲击试验装置[11]Fig.6 Device of single leg landing impact test

4.2 着陆冲击仿真与分析

笔者对单腿垂直着陆工况进行仿真分析，模型采用水平着陆形式，投放高度为0.9 m, 投放质量为305 kg。仿真时间总长为0.3 s，初始时间步长设置为10-7s，仿真结果进行分析并与试验数据进行对比，验证着陆腿模型的正确性与缓冲性能。

仿真工况为标准着陆工况，每条多功能支柱各有两根关于支柱中心轴对称的拉杆。仿真时限制火星车及舱面在竖直方向水平落下，从图7可以看出，两根多功能支柱内四根拉杆缓冲行程曲线基本重合，故对称性十分良好，符合着陆工况特性。

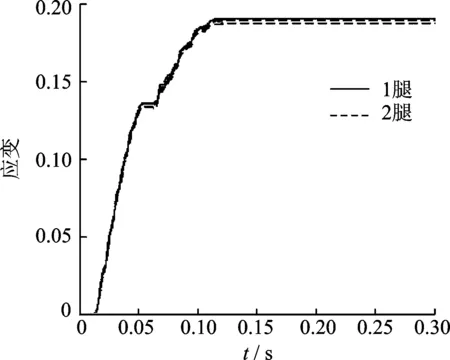
图7 拉杆缓冲行程曲线Fig.7 Rod buffer stroke curve

初始时刻，着陆器距火壤有一定垂直距离，根据工况的投放高度，换算之后给定模型的初速度，在能量分析程序中取测量参考点最低点为势能零点。如图8所示，初始时刻总能为3 498.1 J，缓冲结束后总能稳定在2 605 J左右，整个过程能量耗散为893.1 J，着陆器与火壤间动摩擦为0.42，静摩擦因数为0.5，足垫与火壤间的摩擦力为18 000 N左右，仿真过程足垫滑移大概一个网格，摩擦力做功与能量耗散基本相当。因此，冲击过程满足能量守恒定律，高斯能很小说明没有发生明显沙漏现象和网格畸变。

仿真过程多功能支柱拉杆吸收1 722.7 J能量，限力杆吸收189.8 J，缓冲吸能为1 912.5 J，占初始总能的54.67%，着陆器模型缓冲性能优良。

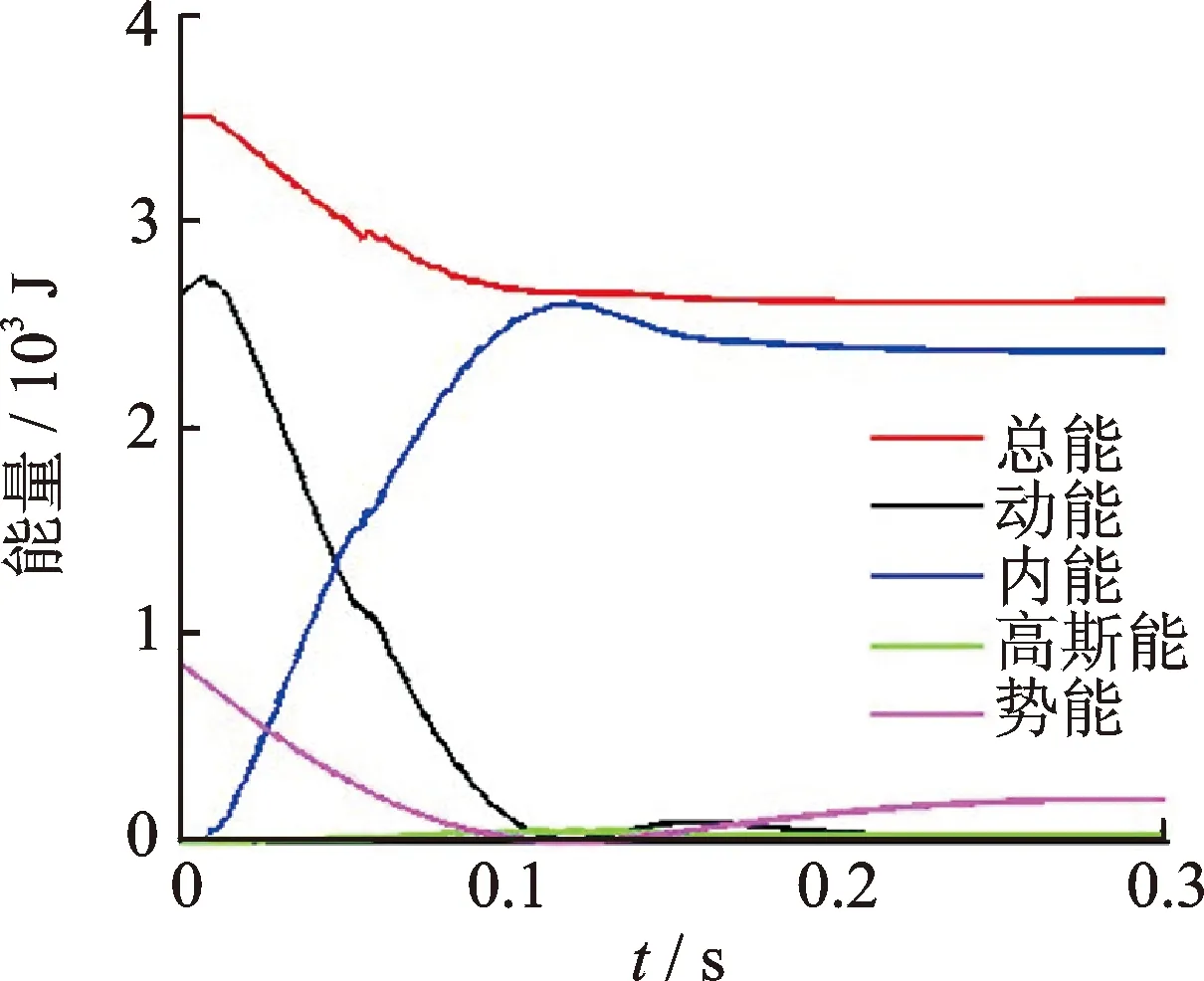
图8 能量分析图Fig.8 Energy analysis diagram

每条多功能支柱包含两根拉杆，拉杆仅能单向拉伸。力从足垫通过内筒向上经由两根拉杆传向与外筒相连的十字梁，拉杆的建模准确性对模型的传力特性影响较大。图9中，蓝色为仿真过程输出的拉杆应力应变曲线，红色为拉杆材料的应力应变场数据拟合出来的曲线，可以看出曲线十分吻合。因此，拉杆的建模是准确的。由图10可以看出，十字梁力与两根拉杆合力十分吻合，由于摩擦原因，十字梁力稍稍大于拉杆合力，模型在0.05 s时刻出现轻微震荡，导致力曲线发生一点变化是符合仿真情理的。因此，着陆器模型的力传载性能十分良好。

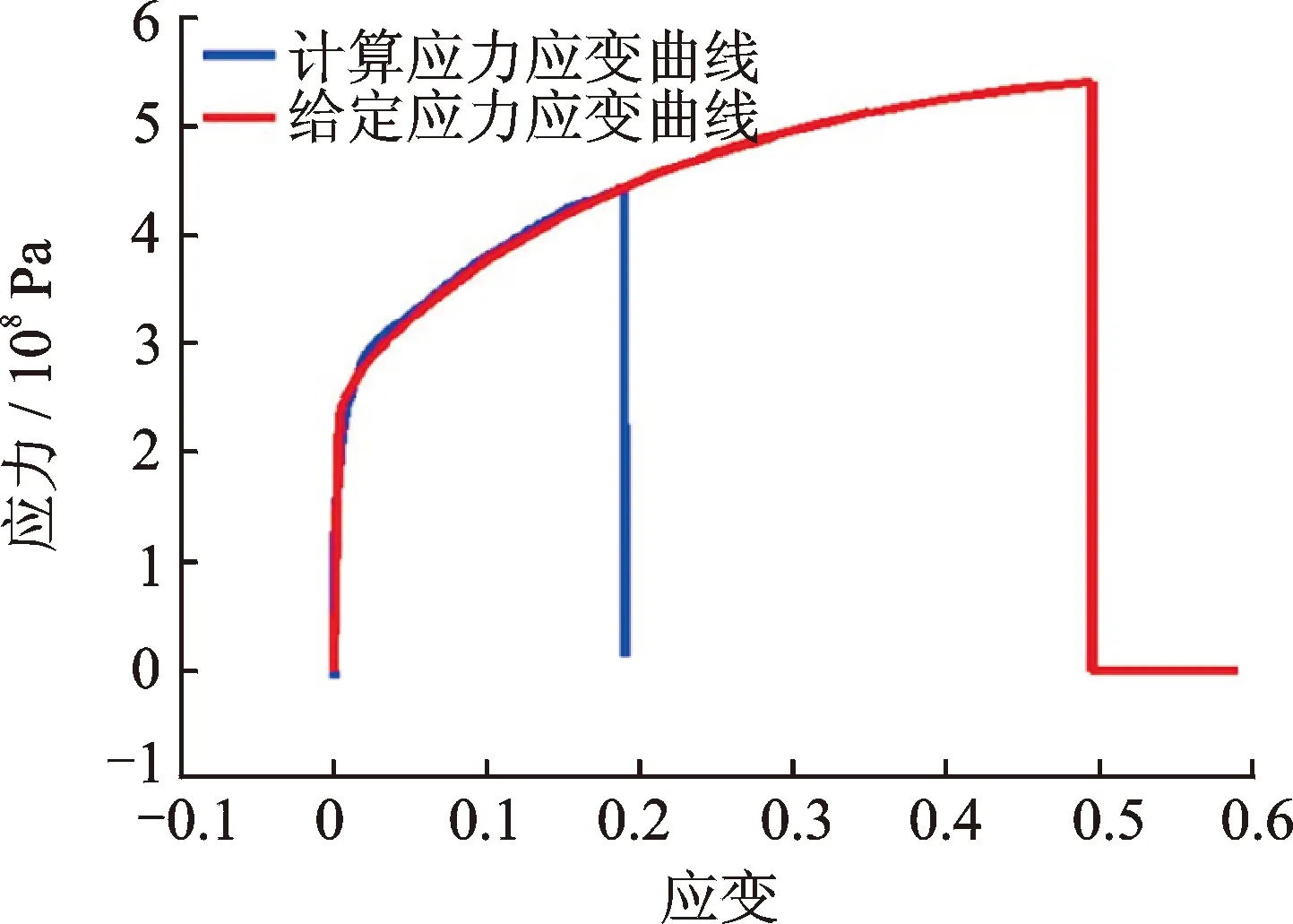
图9 应力应变曲线Fig.9 Stress-strain curve

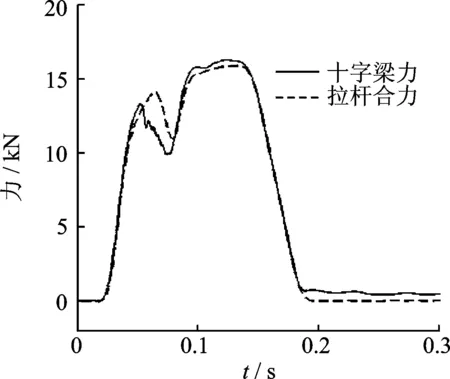
图10 力曲线Fig.10 Force curve

从图11可以看出，着陆器在0.1 s时刻的加速度响应达到最大为4.77g，一般而言，冲击载荷在10g以内，着陆器的机体结构及内部搭载的仪器元件不会发生破坏，均是安全的[12]，从拉杆的缓冲行程曲线可以看出此时缓冲行程也已达到最大。

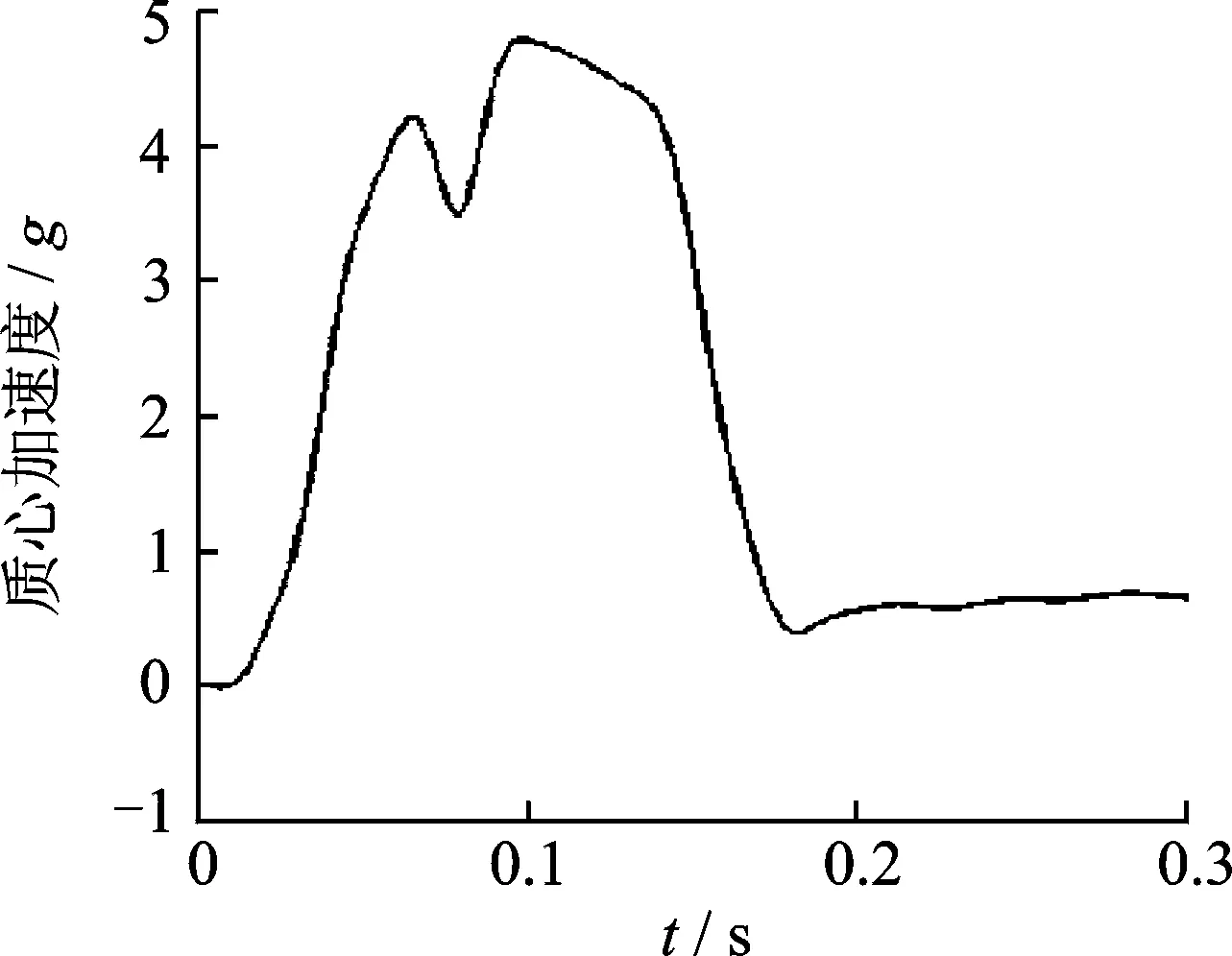
图11 加速度响应曲线Fig.11 Acceleration response curve

仿真结果与试验数据对比如表1所示，仿真结果表明：两根多功能支柱拉杆变形为56.71与57.05 mm，误差为0.34 mm;对应的十字梁力分别为16.23与16.45 kN，误差为0.22 kN,仿真数据十分对称且符合标准对称工况着陆特性。由于试验过程中的设备和安装误差导致试验数据的拉杆变形并不十分对称，从而使试验与仿真的拉杆变形最大误差为13.4%。又因为仿真过程中，内外筒之间面面接触的动静摩擦因数较实际摩擦因数较小，故试验数据相比仿真的十字梁力偏大，模型整体的数据吻合比较良好。

表1仿真结果与试验数据对比

Tab.1Comparisonofsimulationresultswithexperimentaldata

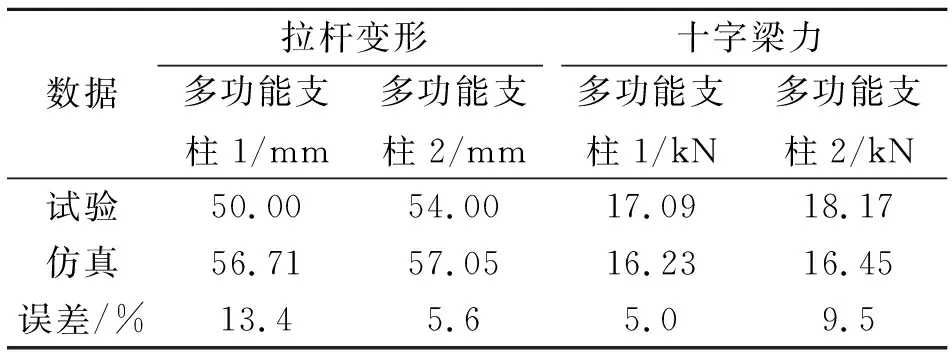
数据拉杆变形十字梁力多功能支柱1/mm多功能支柱2/mm多功能支柱1/kN多功能支柱2/kN试验50.0054.0017.0918.17仿真56.7157.0516.2316.45误差/%13.45.65.09.5

5 结 论

1) 瞬态非线性动力学的建模和显式积分算法能够有效地考虑着陆冲击过程中材料、几何变形和接触的非线性，可以有效地模拟和预测着陆器的冲击过程和缓冲性能。

2) 从仿真结果中可以看出，仿真数据满足单腿标准着陆工况特性；着陆过程模型满足能量守恒；着陆器缓冲和传力性能良好，冲击过程加速度响应满足安全性要求。

3)仿真结果与试验数据的对比表明，火星着陆器有限元建模正确，采用拉杆缓冲的桁架式火星着陆器是完全可行的。