基于小波包样本熵的连续梁桥损伤识别*

孙增寿， 李晓鹏， 韩培琰， 娄文帅

(1.郑州大学土木工程学院 郑州，450001) (2.河南省交通规划设计研究院股份有限公司二分院 郑州，450002)

引 言

目前，基于响应的桥梁结构损伤识别研究多集中在简支梁桥和单跨桥梁，对连续梁桥损伤识别的研究和应用较少。小波包分析是一种精细化的时频分析方法，具有较高的分辨率，能够凸显结构动力响应中损伤信息，所以许多学者对其在结构损伤识别中的应用进行了较为深入的研究。文献[1-2]提出了小波包能量变化率指标，对结构加速度响应信号进行小波包分解，通过能量变化率指标进行损伤定位，可识别三层钢框架结构和简支梁桥的损伤情况。文献[3]基于小波包能量构造结构损伤识别指标，通过数值模拟和试验验证了在斜拉桥结构中的实用性。文献[4]基于曲率和小波包分解，提出了小波包能量曲率差指标，并利用数值模拟和实桥试验对指标的有效性进行了验证。文献[5]通过简支梁数值模拟验证了损伤前后小波包能量变化率平方和指标的有效性。

熵对系统的非线性特性也具有显著的凸显作用，其度量方法有近似熵和样本熵等。样本熵可反映数据序列在某种模式上的自相似度，样本熵值越小，说明序列的自相似性越高，复杂度也越小。实际上，样本熵是近似熵算法的一种改进，克服了近似熵在计算时的偏差。另外，在实际工程中，得到的时间序列数据往往是有限的，而样本熵只需要比较少的数据就可以得到较好的估计值。因此，近年来样本熵被广泛应用于机械故障诊断[6-10]和医学信号处理[11]等领域，并取得了一定的成果。

笔者将小波包变换和样本熵结合起来，更加凸显结构动力响应中的突变信息，更为准确地进行桥梁损伤识别。

1 基本理论

1.1 小波包节点能量

将桥上某点的加速度响应进行小波变换，经过j水平小波包分解后，初始信号f(t)可表示为

(1)

(2)

(3)

1.2 样本熵

假设动力响应{x(n)}=x(1),x(2),…，x(N)的数据个数为N，则其样本熵计算步骤如下。

1) 给定任一维数m，将原始动力响应{x(n)}按序组成一组m维向量序列：Xm(1),Xm(2),…,Xm(N-m+1)，其中Xm(i)={x(i),x(i+1),…,x(i+m-1)}，i=1,2,…,N-m+1。这些序列代表从第i点开始的连续m个x的值。

2) 定义两个向量Xm(i)与Xm(j)之间的距离di,j[Xm(i),Xm(j)]为两者中对应元素最大差值的绝对值，即：

di,j[Xm(i),Xm(j)]=max(|x(i+k)-x(j+k)|)

(4)

其中：k为步长，1≤k≤m-1。

3) 给定一个阈值r，对于给定Xm(i)，统计Xm(i)和Xm(j)之间距离di,j[Xm(i),Xm(j)]≤r的个数j(1≤j≤N-m,j≠i)，并记为Ai。在维数m下，Ai定义为

(5)

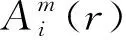
(6)

5) 使维数增加为m+1，对于给定Xm(i)，统计Xm+1(i)和Xm+1(j)之间距离di,j[Xm+1(i),Xm+1(j)]≤r的个数j，并记为Bi。在维数m下，Bi定义为

(7)

(8)

7) 由两个序列在阈值r下匹配m个点的概率Am(r)与两个序列匹配m+1个点的概率Bm(r)的比值定义样本熵

(9)

当样本数据N有限时，用下式估计样本熵值

(10)

由式(10)可以看到，维数m和阈值r两个参数的取值对样本熵Esp(m,r,N)起着至关重要的作用。经试验和分析，当m=1或2，r=0.1Std～0.25Std时(Std为数据x(1),x(2),…,x(N)的标准差)，样本熵的计算结果具有合理的统计特征，这里取m=1，r=0.25Std。

2 损伤指标的构造

2.1 对数加速度能量

加速度能量又称为Appell函数，可表示为

(11)

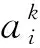
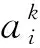
(12)

对特征函数Ea,k取对数，定义对数加速度能量(logarithmic acceleration energy，简称LAE)如下

(13)

当结构发生损伤后，其动力响应也将发生改变，结构振动响应的能量分布也会发生相应的变化。因此，用损伤前后加速度响应的能量差构造损伤识别指标更有助于提高识别效果。

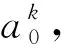
(14)

2.2 结构损伤指标的构造和识别方法

结构动力响应经过小波包变换后，凸显出了动力响应信号中的局部损伤特征；样本熵可进一步利用上述有限数据得到稳定的统计值，且有一定的抗噪能力。将二者结合起来，建立对数加速度能量差小波包样本熵指标进行结构损伤识别，会达到更好的识别效果。

基于小波包样本熵的结构损伤识别方法，主要是对信号进行小波包变换后，选择频带归一化能量最大的组分对其进行重构，然后计算重构信号的样本熵值，根据样本熵值的大小判断其损伤状态。针对连续梁损伤识别，结合对数加速度能量，提出了对数加速度能量差小波包样本熵指标(sample entropy of wavelet packet transform of difference of logarithmic acceleration energy，简称ESPL)。结构损伤识别流程如图1所示。

图1 结构损伤识别流程图Fig.1 Flow diagram of structural damage identification

1) 在桥梁建成通车前，利用标准载重车辆匀速通过连续梁桥，采集得到梁桥完好状态下桥上任一点的加速度响应数据；

2) 桥梁运营过程中，利用相同载重车辆以相同速度匀速通过连续梁桥，采集得到桥梁当前状态下桥上同一点的加速度响应数据；

3) 利用式(14)计算动力响应的对数加速度能量差DLAE；

4) 对DLAE进行小波包分解，根据式(3)计算得到各个组分的小波包能量，选择能量最大的组分进行信号重构；

5) 将重构信号划分为n个时间区间，由式(10)计算每个区间的样本熵值，即ESPL(1)，ESPL(2)，…,ESPL(n)；

6) 根据样本熵序列大小进行结构损伤识别。

3 数值算例

3.1 工程概况及建模

以某三跨变截面钢筋混凝土连续梁桥为例，桥全长110 m，跨径布置为30 m+50 m+30 m。主梁断面为单箱单室箱形截面，梁底按抛物线变化，箱梁根部高4.2 m，跨中截面高2.1 m。箱梁顶板宽度为12.8 m， 设置有2%的双向横坡。箱梁底板宽度为6 m。主梁采用C50混凝土。横截面如图2所示。

图2 连续梁桥主梁横截面图(单位：cm)Fig.2 Cross section graph of continuous beam bridge (unit: cm)

用有限元方法进行建模和分析，采用beam189单元，单元长度取2.5 m，材料弹性模量E=3.45×104MPa，剪切模量G=1.38×104MPa，密度ρ=2 500 kg/m3。整个梁桥共划分为44个单元，两个边跨分别有12个单元，单元编号分别为1～12和33～44，中跨有20个单元，单元编号为13～32，假定单元6，23和40存在损伤，采用降低单元刚度的方法模拟损伤，损伤程度用δ表示，具体损伤工况如表1所示。梁桥有限元模型如图3所示，图中黑色部分即为损伤位置。在中跨跨中位置放置一个加速度传感器，采集中跨跨中位置处的加速度响应。

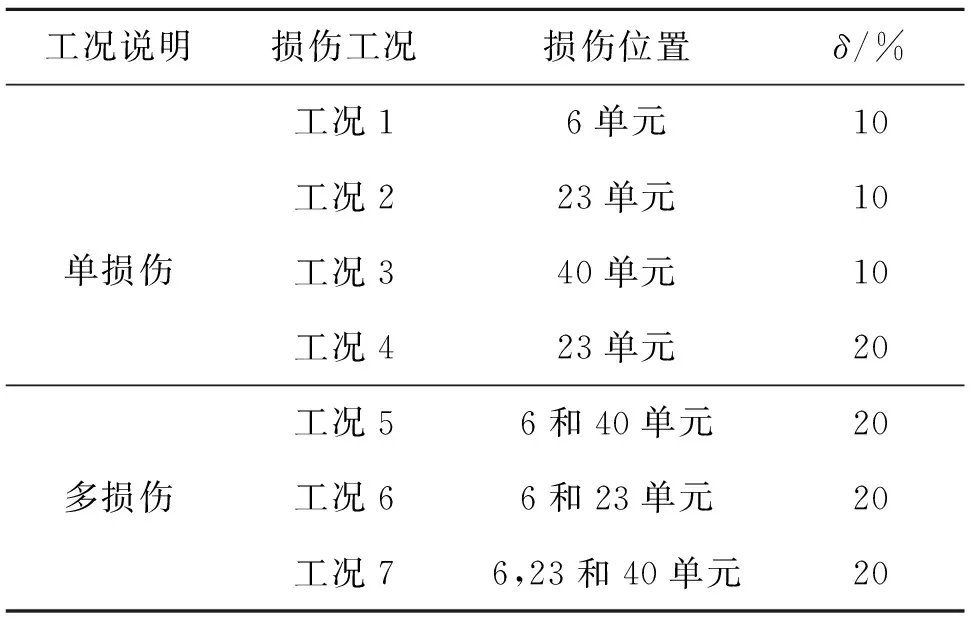
表1 损伤工况

图3 连续梁桥单元划分图Fig.3 Units classification of continuous beam bridge

3.2 梁桥损伤识别

利用损伤指标ESPL进行损伤识别时，选择车辆荷载大小为F=100 kN，以v=10 m/s的速度匀速通过全桥，采集中跨跨中位置处的加速度响应，采样点数为2 200。然后利用基于MATLAB编制的专用程序，计算对数加速度能量差小波包样本熵指标(ESPL)。计算过程中，把整个加速度响应信号划分为44个区段(即每个单元长度对应一个区段，每个区段的数据个数为50)。以下为各个损伤工况的分析及识别结果。

3.2.1 单处损伤识别

在单处损伤情况下，工况1～工况4的ESPL计算结果见图4～图7所示。为了更直观地判断损伤位置，对ESPL值进行数理统计分析后引入置信上限，且对损伤指标设置阈值，置信概率取95%，阈值见各图中的水平线。由图4可知，在单元6位置处，损伤指标ESPL值明显大于其他单元处的指标值和阈值，说明此处发生了损伤，与假设的损伤位置一致。虽然在其他单元处也有显现，但数值都较小，不影响损伤位置判断。由图5～6同样也可以看出，23与40号单元发生了损伤，与假定的损伤单元均一致。说明利用ESPL指标进行单处损伤识别具有良好的效果。对比图5和图7可以发现，虽然在23号单元处损伤指标值都取得最大，但是工况2和工况4中23号单元的损伤指标值分别为1.05和1.32，相差较大，说明损伤程度不同，结构损伤指标的数值也不同。随着损伤程度的增大，损伤指标的值也增大。

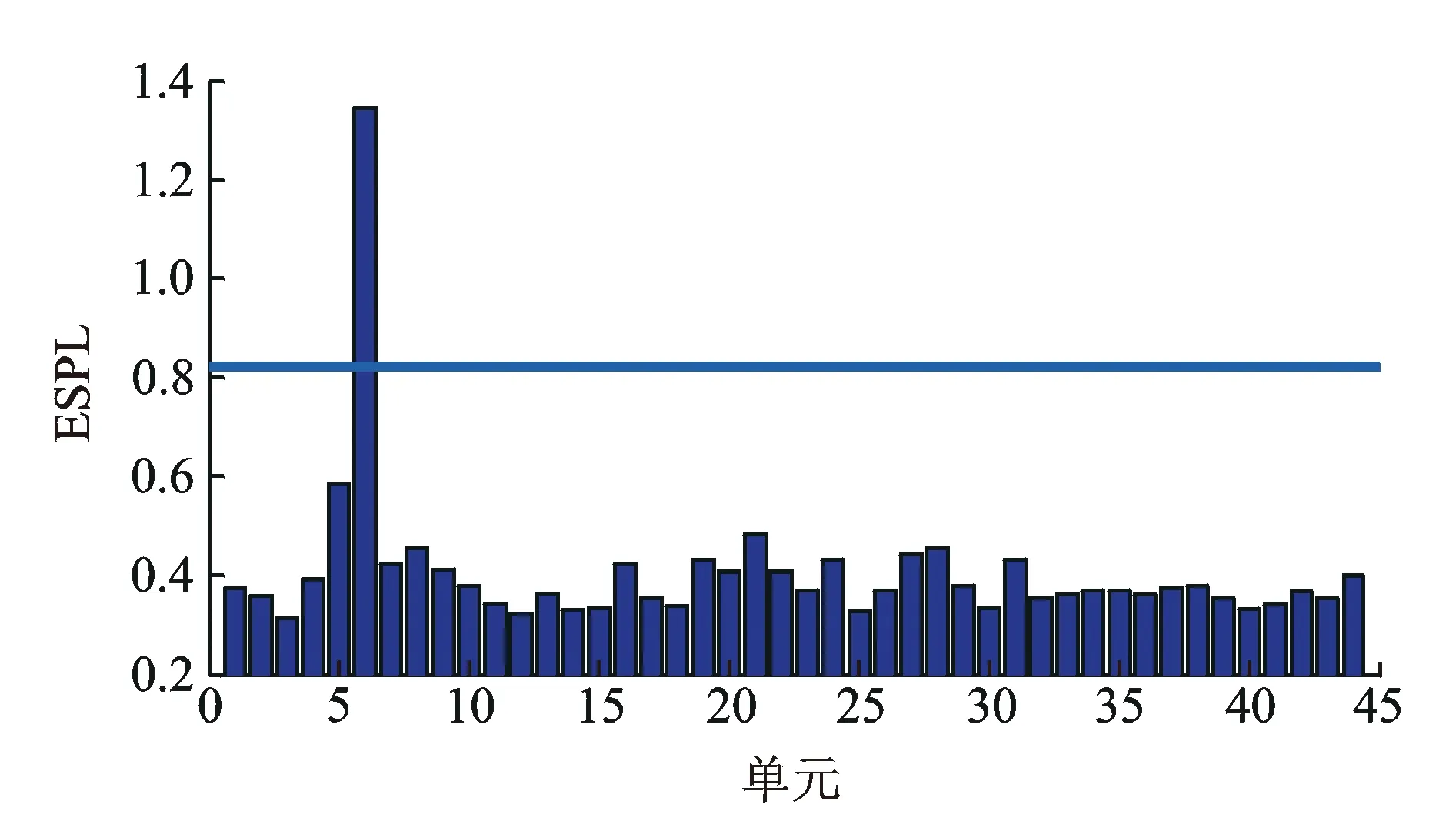
图4 工况1损伤指标ESPL值Fig.4 The damage index ESPL under condition 1

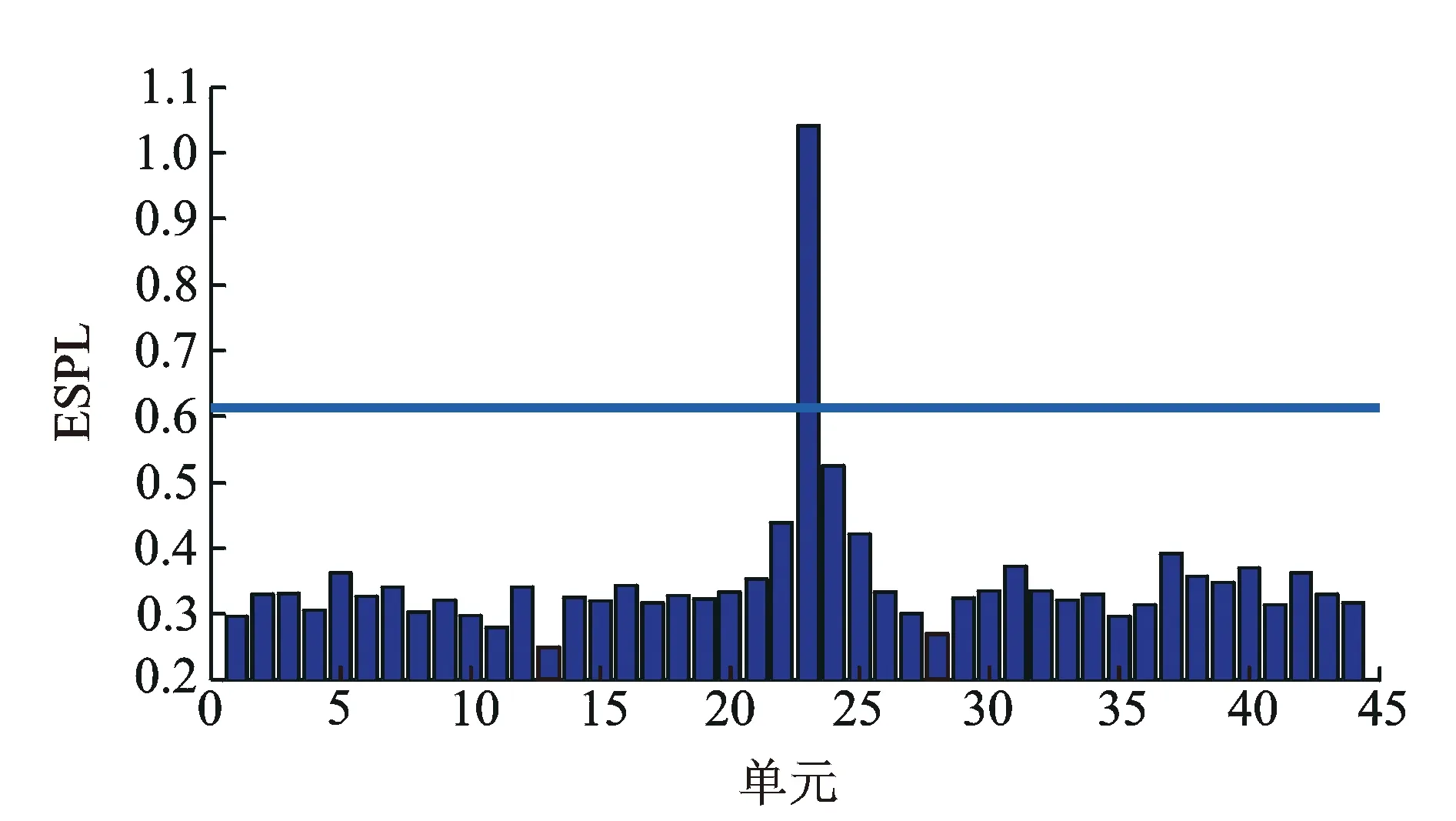
图5 工况2损伤指标ESPL值Fig.5 The damage index ESPL under condition 2

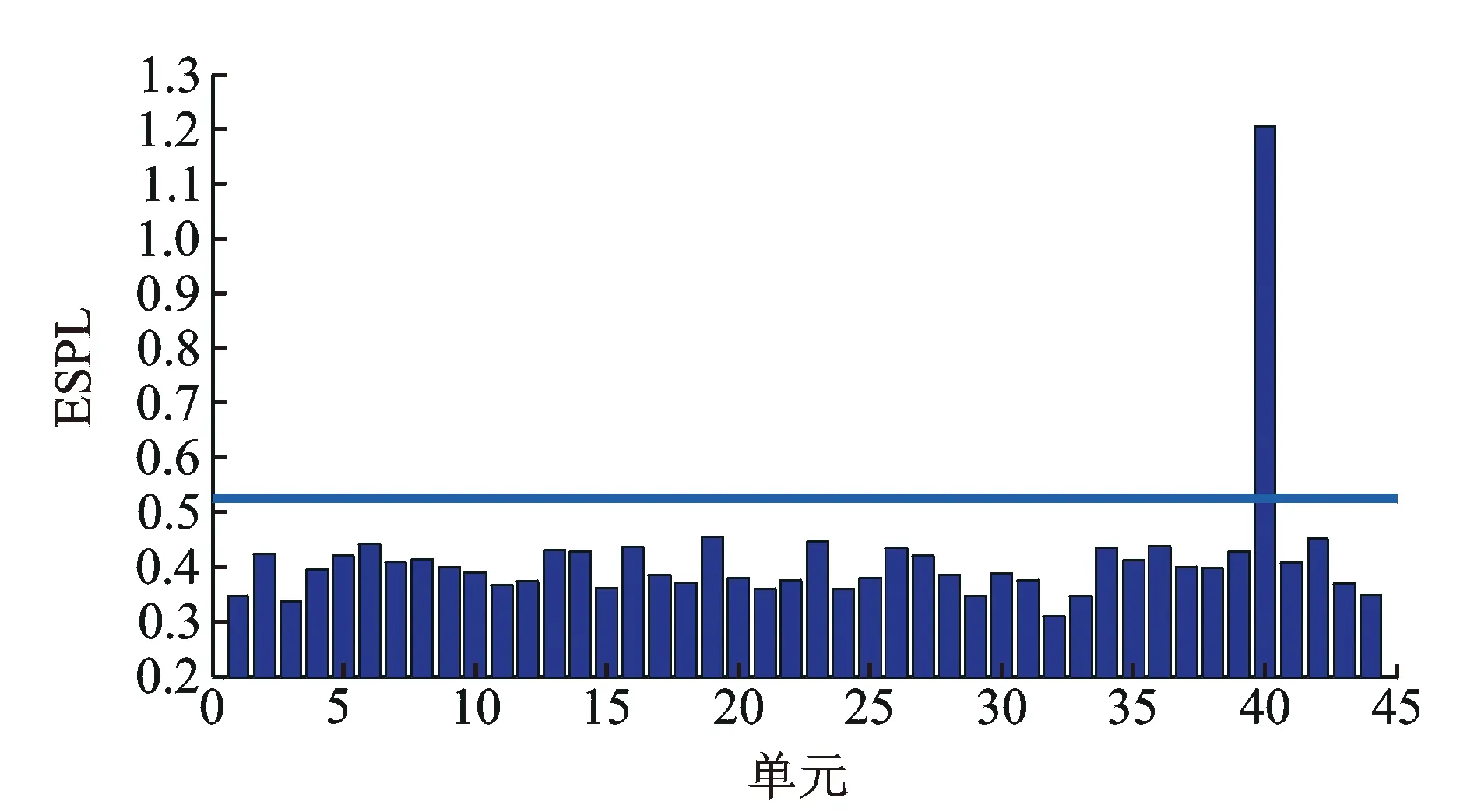
图6 工况3损伤指标ESPL值Fig.6 The damage index ESPL under condition 3

图7 工况4损伤指标ESPL值Fig.7 The damage index ESPL under condition 4

3.2.2 多处损伤识别

当结构存在多处损伤时，各损伤之间存在相互影响的问题，需对指标的适用性及其变化规律做进一步考察。对损伤工况5～工况7进行分析研究，相应的损伤识别结果见图8～10所示。

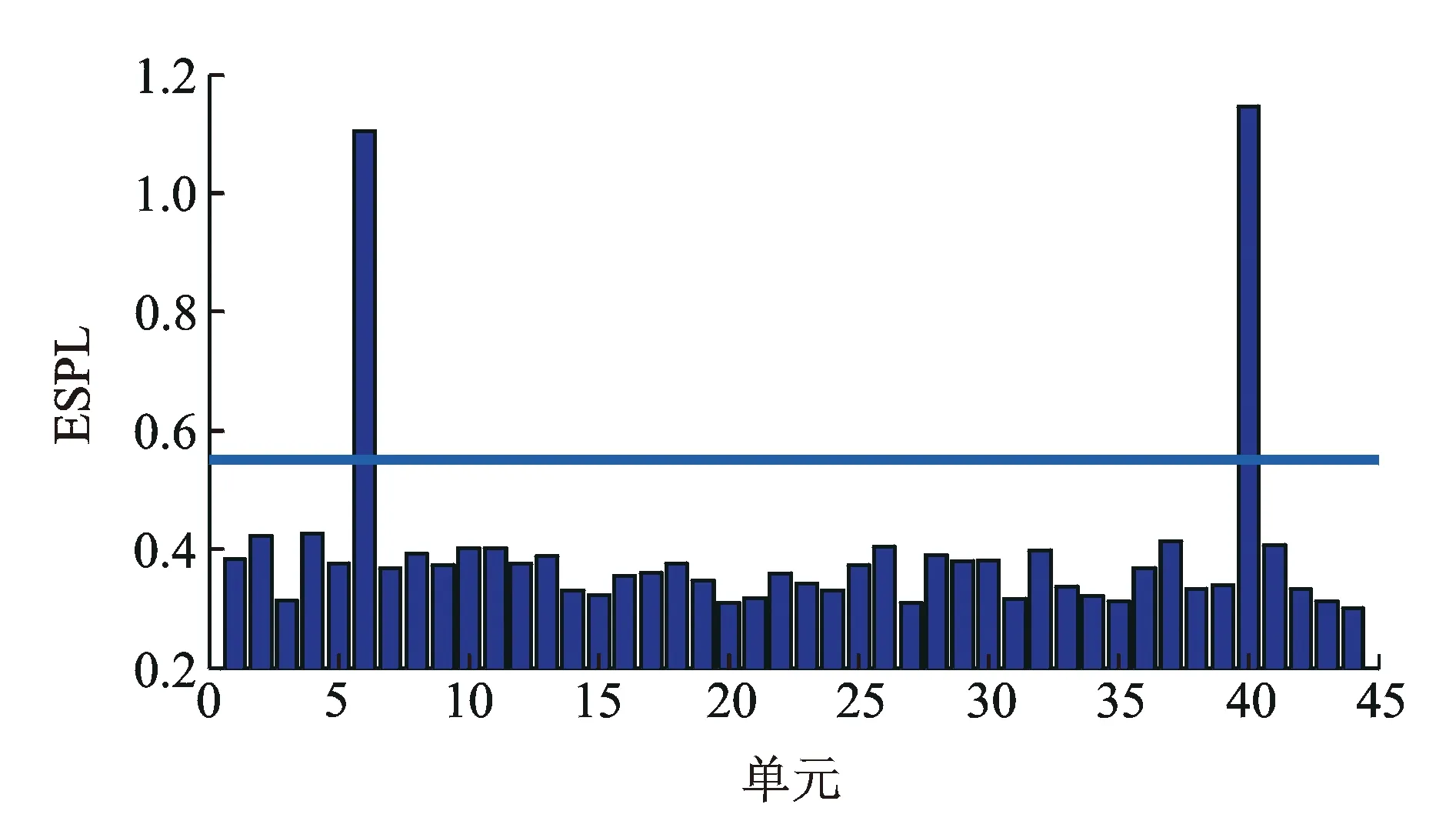
图8 工况5损伤指标ESPL值Fig.8 The damage index ESPL under condition 5

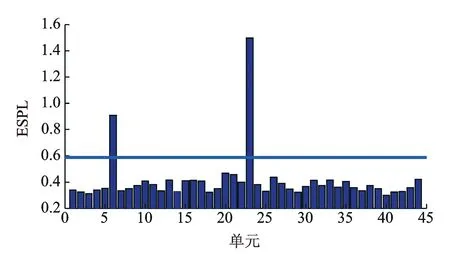
图9 工况6损伤指标ESPL值Fig.9 The damage index ESPL under condition 6

图10 工况7损伤指标ESPL值Fig.10 The damage index ESPL under condition 7

从图8可以看出，当结构存在两处损伤时，损伤指标ESPL在6号和40号单元的值明显大于其他单元，说明在这两处存在损伤，与假设损伤位置一致。从图9同样可以看出，6号和23号单元存在损伤。从图10可以看出，当结构存在三处损伤时，单元6，23和40处的损伤指标值最大，说明该指标也能够对三处损伤进行识别。

3.2.3 损伤程度估计

当损伤位置确定后，需进一步对桥梁的损伤程度进行估计。为了确定损伤指标与损伤程度之间的对应关系，为损伤程度估计提供依据，对不同损伤程度下的损伤指标进行分析。假设中跨跨中位置损伤，损伤程度δ分别为10%，20%，30%和40%。在相同载重和速度的车辆作用下，不同损伤程度下的损伤指标ESPL值见图11所示。由图可知，随着损伤程度不断增大，虽然各位置的指标值的振荡性有所增加，但中跨跨中的指标值始终是最大的，并不影响损伤位置的识别。而且随损伤程度δ增大，损伤位置处的ESPL指标值也不断增大，可根据损伤指标ESPL对损伤程度进行估计。

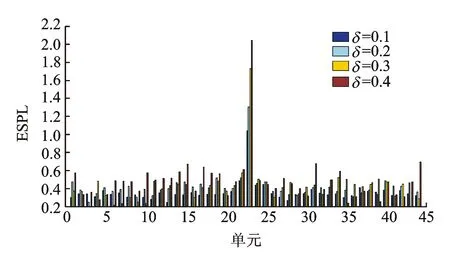
图11 不同损伤程度下的指标ESPL值Fig.11 The ESPL under different extent damage

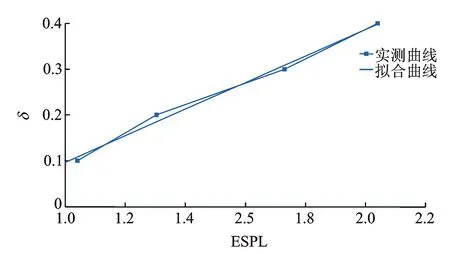
图12 损伤单元处的δ-ESPL曲线Fig.12 The δ-ESPL curves at damage position

图12为不同损伤程度下的δ-ESPL拟合曲线图，损伤程度δ和损伤指标ESPL大致呈线性递增关系。由最小二乘法可建立曲线的函数表达式，进而根据损伤指标值估计梁桥的损伤程度。

3.3 噪声鲁棒性分析

在桥梁现场测试中，由于测量环境和设备等因素的影响，结构响应信号中不可避免的存在噪声。为了分析所提出损伤识别方法和损伤指标的工程适用性，在上述加速度响应信号中添加不同水平的噪声。以工况2为例，在跨中加速度响应信号中分别附加5%和10%水平的噪声。含噪加速度响应为

ad,n=ad+EPNnσ(ad)

(15)

其中：ad,n为含噪声的加速度响应；EP为噪声水平；Nn表示噪声服从标准正态分布；σ(ad)为无噪加速度响应的均方差。

利用图1方法和流程对含噪加速度响应进行分析，分析结果见图13所示。从图13可见，当存在10%的噪声时，中跨跨中位置处的损伤指标ESPL值依然取得最大值，仍然能够很好地识别出损伤位置。但是随着噪声水平的不断提高，未损伤位置处的指标值也会增大，其波动性越来越强。因此，在高水平噪声影响下，结构的损伤信息可能会被淹没，影响结构损伤的识别。

图13 噪声对损伤指标ESPL的影响Fig.13 The noise influence on damage index ESPL

4 结 论

1) 利用连续梁桥上单个测点的加速度响应即可识别全桥各跨的损伤情况，且识别效果较好，可减少以往测量中的传感器数量和现场布设工作。

2) 对数加速度能量差小波包样本熵指标不仅可以识别桥梁单处与多处损伤的位置，而且能够对损伤程度进行估计。

3) 对数加速度能量差小波包样本熵指标和损伤识别方法具有较好的鲁棒性，在噪声水平为10%时仍具有较好的识别效果。